在前面,我们学习了线性表和树,而接下来我们要学习的图相较于他们就更加复杂。
目录
一.图的有关概念
一.图的有关概念
1.定义
图(graph)G由两个集合V和E组成,记为G=(VE)。V是顶点的有穷非空集合;E是边的集合,边是V中顶点的无序对或有序对。E可以是边的空集,者E为空集,则G中只有顶点没有边。
2.由于“弧”是有方向的,因此称由顶点集和弧集构成的图为有向图。
3.顶点:在图中的数据元素
4.弧:若<v,w> VR,则<v,w>表示从v到w的一条弧
弧尾:v(起始点)
弧头:w(终端点)
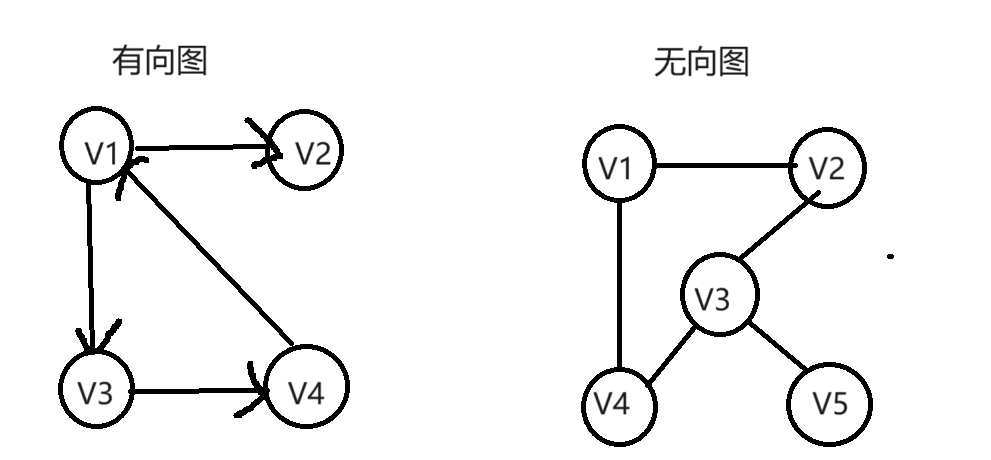
5.有向图:是图论中的一种重要概念,用于描述各种事物之间的有序关系。它由一组节点(或顶点)以及连接这些节点的有向边组成。每条边都有一个方向,从一个节点指向另一个节点,表示了它们之间的关系和方向性
无向图:边没有方向的图
6.完全图:有n(n-1)/2条边的无向图
有向完全图:对于有向图,e的取值范围是0到n(n-1),具有n(n-1)条弧的有向图
无向完全图:n个顶点的无向图,每个顶点与其他n-1个顶点都有边,具有最大边数n(n-1)/2
7.稀疏图:有很少条边或弧的图
稠密图:图的边或弧很多
8.权:与图的边或弧相关的数
网:带权的图
9.邻接点:假若顶点v和顶点w之间存在一条边,那么v和w互为邻接点
10.度:无向图中,与其相关联的边的数目
入度:(有向图)以顶点v为头的弧的数目
出度:(有向图)以顶点v为尾的弧的数目
11.路径长度:沿路径边的数目或沿路径各边权值之和
回路:第一个顶点和最后一个顶顶点相同的路径
简单路径:序列中顶点不重复出现的路径
简单回路:除了第一个顶点和最后一个顶点外,其余顶点不重复出现的回路
12.连通:无向图中如果从顶点V到顶点W有一条路径,则说V和W是连通的
连通图:无向图中任意两个顶点都是连通的
连通分量:无向图中的极大连通子图
强连通分量:有向图中的极大强连通子图
13.生成树:一个极小连通子图,它含有图中全部顶点,但只有足以构成一棵树的n一1条边
二.图的存储结构
2.1.图的数组(邻接矩阵)存储表示
2.1.1图的邻接矩阵表示法的特点
·对于无图:
邻接矩阵一定是一个对称矩阵
行(列)非零元素个数,表示度
·对于有向图:
矩阵不一定是一个对称矩阵
行非零元素个数,表示出度
·列非零元素个数,表示入度
2.1.2应用
通过邻接矩阵判定任意两个顶点之间是否有边相连

2.邻接表
是图的一种链式存储结构
特点
无向图中顶点VI的度为第1个单链表中的结点
有向图中
顶点Vi的出度为第1个单链表中的结点个
顶点Vi的入度为整个单链表中邻接点城#
值是的结点个数
逆邻接表:有向图中对每个结点建立以Vi为头
的弧的单链表