片头
嗨!大家好,今天我们来练习几道二叉树的题目来巩固知识点,准备好了吗?Ready Go ! ! !

第一题:二叉树的最大深度

解答这道题,我们采用分治思想
1. 递归子问题:左子树的高度和右子树的高度
高度 = 比较左子树的高度和右子树的高度,取较大的,最后将结果加1
2. 返回条件(最小子问题):结点为空,空的高度为0
为啥 高度 = Max(左子树,右子树)+1 呢? 因为我们求出左右子树中较大的一个,但是子树和根节点还有1个单位的距离,因此,我们必须将比较的结果加1。
举个例子吧~

这道题的代码如下:
int maxDepth(struct TreeNode* root) {
//如果根节点为空,返回0
if(root == NULL){
return 0;
}
//h1表示左子树的高度
//h2表示右子树的高度
int h1 = maxDepth(root->left);
int h2 = maxDepth(root->right);
//比较h1和h2,取较大的值+1 (加1表示从子树到根节点的距离)
return h1>h2 ? h1+1 : h2+1;
}第二题:相同的树

举个例子~

那这道题的思路是什么呢?
很简单,把两棵树都拆分成 根、左子树、右子树 ,一一进行比较,第一轮比较完毕后,将左子树又拆分成 根、左子树、右子树, 第二轮比较完毕后,将右子树拆分成 根、左子树、右子树........依次类推,如果其中一个结点为空,另外一个结点非空或者相同位置的结点对应的值不相等,返回false

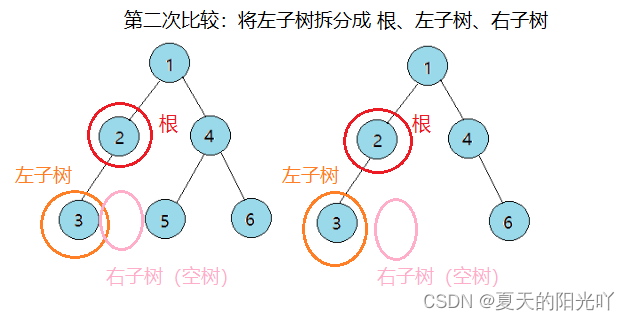

OK啦,这道题的整体代码如下:
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
//如果p和q同时为空,返回true
if(p == NULL && q == NULL){
return true;
}
//如果p为空,q非空,返回false
//如果q为空,p非空,返回false
if(p == NULL || q == NULL){
return false;
}
//如果p指向结点的值不等于q指向的结点的值,返回false
if(p->val != q->val){
return false;
}
//继续将p的左子树和q的左子树进行比较
//继续将p的右子树和q的右子树进行比较
return isSameTree(p->left,q->left)
&& isSameTree(p->right,q->right);
}第三题:单值二叉树

所谓的单值二叉树的意思是:二叉树中所有结点的值都为同一个值,如果哪一个结点的值和其他结点不同,那么就不是单值二叉树。

怎么判断这棵二叉树是否为单值二叉树呢?
思路:从根节点开始,依次比较根节点的左子树和右子树的值是否与根节点的值相等。①先判断根节点的左子树是否存在,如果左子树存在,②并且左子树结点的值和根节点的值不相等,返回false; 然后判断根节点的右子树是否存在,如果右子树存在,并且右子树结点的值和根节点的值不相等,返回false。比较到什么时候结束呢?当比较的结点为空时,递归结束。(注意:如果根节点为空,也符合题意,返回true)。 只要有其中一个左子树(右子树)的结点与根节点不相同,就立即返回false,因此用短路与&& 连接。
这道题的代码如下:
bool isUnivalTree(struct TreeNode* root) {
//如果根节点为空,返回true
if(root == NULL){
return true;
}
//如果根节点的左孩子存在,并且左孩子的值和根节点的值不相同,返回false
if(root->left && root->left->val != root->val){
return false;
}
//如果根节点的右孩子存在,并且右孩子的值和根节点的值不相同,返回false
if(root->right && root->right->val != root->val){
return false;
}
//继续比较根节点的左孩子和根节点的右孩子
//如果其中一个结点的值和根节点的值不相同,立即返回false
//因此用短路与&&连接
return isUnivalTree(root->left)
&& isUnivalTree(root->right);
}第四题:对称二叉树

对称二叉树是一种特殊的二叉树结构,它的左子树和右子树镜像对称。换句话说,对称二叉树的左子树和右子树可以互相翻转得到相同的结构。
对称二叉树具有以下性质:
1. 根节点的左子树和右子树对称。
2. 左子树的左子树与右子树的右子树对称。
3. 左子树的右子树与右子树的左子树对称。
可以通过比较根节点的左右子节点是否相等,以及递归地比较左子树的左子节点与右子树的右子节点,左子树的右子节点与右子树的左子节点,来判断二叉树是否对称
emmm,有点抽象,咱们画个图呗~

以根节点为分界线,依次比较根节点的左子树和右子树,看看是否对称
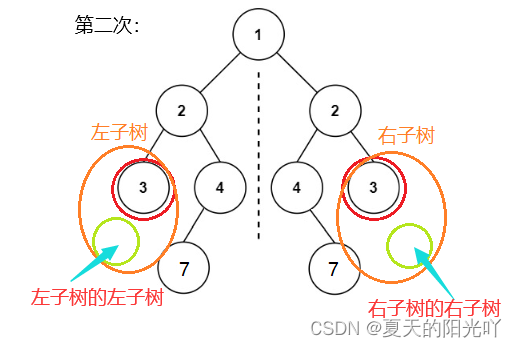

所以,其实这道题和相同的树有点类似,都是先比较根节点,再比较根节点的左右子树。但是相同的树是直接左子树和左子树进行比较,右子树和右子树进行比较;对称二叉树是左子树和右子树进行比较, 左子树的左子树与右子树的右子树进行比较,以及左子树的右子树与右子树的左子树进行比较。
代码如下:
bool _isSymmetric(struct TreeNode* root1,struct TreeNode* root2){
//如果root1和root2同时为空,返回true
if(root1 == NULL && root2 == NULL){
return true;
}
//如果root1为空,root2非空,返回false
//如果root1为非空,root2为空,返回false
if(root1 == NULL || root2 == NULL){
return false;
}
//如果root1指向结点的值不等于root2指向结点的值,返回false
if(root1->val != root2->val){
return false;
}
//比较root1的左子树和root2的右子树
//比较root1的右子树和root1的左子树
return _isSymmetric(root1->left,root2->right)
&& _isSymmetric(root1->right,root2->left);
}
bool isSymmetric(struct TreeNode* root) {
//将root的左右子树进行比较,最后将结果返回
return _isSymmetric(root->left,root->right);
}第五题:另一棵树的子树
举个例子呗~

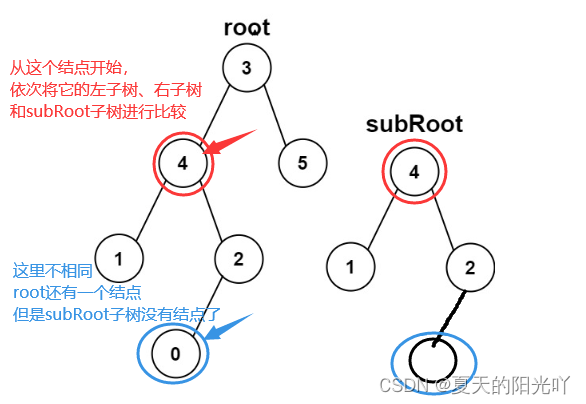
因此,这道题的要求实质上就是将subRoot这棵树和root这棵树的每一棵子树进行比较。那么怎么找到原树里面的每一棵子树?遍历root这棵树就能找到原树里面的每一棵子树。
root这棵树的每一个结点都是subRoot这棵树的根,将每一个结点和subRoot这棵树一一比较。
subRoot这棵树与原树的每一棵子树进行比较,怎么拿到子树呢?遍历
这道题要用到树的比较这种思想,因此我们可以复用相同的树里面的方法,我们把代码先拿过来~
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
//如果p和q同时为空,返回true
if(p == NULL && q == NULL){
return true;
}
//如果p为空,q非空,返回false
//如果q为空,p非空,返回false
if(p == NULL || q == NULL){
return false;
}
//如果p指向结点的值不等于q指向的结点的值,返回false
if(p->val != q->val){
return false;
}
//继续将p的左子树和q的左子树进行比较
//继续将p的右子树和q的右子树进行比较
return isSameTree(p->left,q->left)
&& isSameTree(p->right,q->right);
}接着,我们就可以在题目提供的方法中写代码了,注意:根节点root不可能为空,但是root这棵树的子树有可能为空,因为subRoot子树不可能为空,如果在root子树中遇到空节点,返回false
//如果root二叉树的子树为空,返回false
if(root == NULL){
return false;
}在遍历的过程中,
我们先和当前根进行比较。如果在当前根root与subRoot的值相同,以及root的左右子树和subRoot都相同,说明我们在当前根root里面找到了subRoot子树,返回true;
如果不相等,我先到左子树去查找有没有和subRoot相同的树,如果找到了,就不需要到右子树查找了;如果没找到,那么继续去右子树查找有没有和subRoot相同的树。
所以,我们用短路或||来连接(有点类似BinaryTreeFind函数,查找与x相同的结点,但是这里是查找和subRoot相同的树(子树))
//在当前子树中未找到和subRoot相同的子树
//继续比较root的左子树和root的右子树,看是否能找到subRoot
//一旦找到和subRoot相同的子树,立即返回true,因此用短路||连接
return isSubtree(root->left,subRoot)
|| isSubtree(root->right,subRoot);我在遍历root这棵树,每棵子树都会出现;如果root->val == subRoot->val,说明两个根的值相同(如果根不相同就没办法进行比较了),接着再比较2棵子树是否完全相同,调用isSameTree方法,如果完全相同,返回true;否则继续往下递归比较。
//如果root结点的值和subRoot结点的值相同
//并且root的左右子树和subRoot子树完全相同,才能返回true
if(root->val == subRoot->val && isSameTree(root,subRoot)){
return true;
}OK啦,这道题被我们解决了,整体代码如下:
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
//如果p和q同时为空,返回true
if(p == NULL && q == NULL){
return true;
}
//如果p为空,q非空,返回false
//如果q为空,p非空,返回false
if(p == NULL || q == NULL){
return false;
}
//如果p指向结点的值不等于q指向的结点的值,返回false
if(p->val != q->val){
return false;
}
//继续将p的左子树和q的左子树进行比较
//继续将p的右子树和q的右子树进行比较
return isSameTree(p->left,q->left)
&& isSameTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
//如果root二叉树的子树为空,返回false
if(root == NULL){
return false;
}
//如果root结点的值和subRoot结点的值相同
//并且root的左右子树和subRoot子树完全相同,才能返回true
if(root->val == subRoot->val && isSameTree(root,subRoot)){
return true;
}
//在当前子树中未找到和subRoot相同的子树
//继续比较root的左子树和root的右子树,看是否能找到subRoot
//一旦找到和subRoot相同的子树,立即返回true,因此用短路||连接
return isSubtree(root->left,subRoot)
|| isSubtree(root->right,subRoot);
}第六题:二叉树的前序遍历

有的小伙伴可能会说:二叉树的前序遍历?哈哈哈哈,太简单了,的确,单纯地写一个前序遍历难不倒我们,但是这道题的要求是将前序遍历的结果放入数组中。

首先,我们来观察一下这道题给我们的2个参数,第一个参数表示一个二叉树的根节点,那么第二个参数表示什么呢?
returnSize这个值表示数组的大小,返回值为int* 类型,表示我既要返回这个数组,也要返回数组的大小,这样的话,别人才方便测试。
在leetcode上面有统一模式的规定:只要返回数组,必须得返回数组的大小
那么问题来了:数组需要开辟多大空间?
想法1:像顺序表一样,初始时开辟4个空间,后面如果空间不足,可以进行扩容。但是,扩容分2种情况:如果后面的空间足够,那么就原地扩容;如果后面的空间不足,只能异地扩容,那么代价很大。另外,如果题目给的二叉树结点很多,频繁扩容会导致效率低下。
想法2:一次性直接开满。这个想法是不可行的,容易造成空间浪费
(推荐)想法3:求二叉树的大小,树有多大,就给数组开辟多大的空间。
因此,求二叉树的结点个数的代码如下:
int TreeSize(struct TreeNode* root){
//求二叉树的结点个数
//如果根节点为空,返回NULL
//如果根节点非空,返回左子树的个数+右子树的个数+1(自己)
return root == NULL ? 0 :
TreeSize(root->left)+TreeSize(root->right)+1;
}算出来二叉树的结点个数,我们就可以在题目提供给我们的方法进行使用了。
不过,有一个小问题: 为啥形参returnSize的是int* 类型的呢?很简单,因为如果是int类型,形参是实参的临时拷贝,修改形参不会影响到外面的实参,所以我们需要传指针,将实参的地址传给形参,对形参解引用,访问的是外面的实参。
OK,了解完这些后,我们来解答这道题~
//用*returnSize 来接收返回过来的TreeSize
*returnSize = TreeSize(root);
//数组开辟 *returnSize 个大小的空间
int* a = malloc(sizeof(int)*(*returnSize));数组开辟完毕,接下来我们就要将二叉树里面节点的数据依次放入数组中。我们首先定义一个 preorder函数,把二叉树的根节点root,数组a,还有下标i的地址传递过去。
//定义变量i,表示数组的下标从0开始
int i = 0;
//前序遍历,依次将结点里面的数据放入数组中
preorder(root,a,&i);
//最后返回a数组
return a;为啥传递下标i的地址呢?因为递归调用会建立多个栈帧,如果我们希望在递归期间栈帧里面只有1个下标,那么必须传递下标i的地址,用 int* pi 来接收i的地址,对pi进行解引用,(*pi)表示i。
前序遍历的代码如下:
void preorder(struct TreeNode* root,int* a,int* pi){
//如果根节点为空,返回NULL
if(root == NULL){
return;
}
//将结点的数据依次拷贝到a数组中,每拷贝完一次,下标指向下一个位置
a[(*pi)++] = root->val;
//继续递归根的左子树
preorder(root->left,a,pi);
//继续递归根的右子树
preorder(root->right,a,pi);
}欧克欧克,整体代码如下:
int TreeSize(struct TreeNode* root){
//求二叉树的结点个数
//如果根节点为空,返回NULL
//如果根节点非空,返回左子树的个数+右子树的个数+1(自己)
return root == NULL ? 0 :
TreeSize(root->left)+TreeSize(root->right)+1;
}
void preorder(struct TreeNode* root,int* a,int* pi){
//如果根节点为空,返回NULL
if(root == NULL){
return;
}
//将结点的数据依次拷贝到a数组中,每拷贝完一次,下标指向下一个位置
a[(*pi)++] = root->val;
//继续递归根的左子树
preorder(root->left,a,pi);
//继续递归根的右子树
preorder(root->right,a,pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
//用*returnSize 来接收返回过来的TreeSize
*returnSize = TreeSize(root);
//数组开辟 *returnSize 个大小的空间
int* a = (int*)malloc(sizeof(int)*(*returnSize));
//定义变量i,表示数组的下标从0开始
int i = 0;
//前序遍历,依次将结点里面的数据放入数组中
preorder(root,a,&i);
//最后返回a数组
return a;
}第七题:二叉树遍历

题目要求的是先输入前序遍历的字符串,然后根据字符串建立二叉树,建立起二叉树后,再对二叉树进行中序遍历,输出结果。
咱们先不慌做题,先来看看根据字符串如何构建二叉树过程~

再来看一个例子~
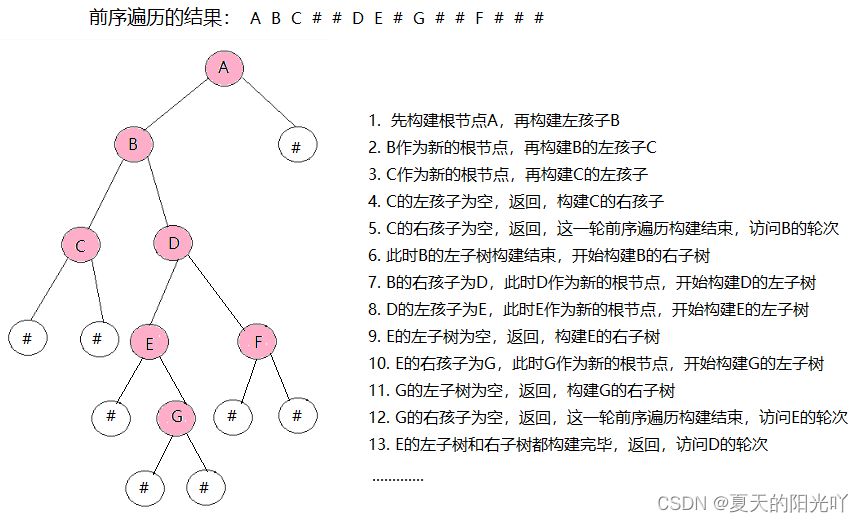
OK啦,了解完构建二叉树的过程后,我们可以开始做题啦~
emmm,既然是通过字符串来构建二叉树,那么必须得有数组来存放字符串吧,是不是~
//输入包括1行字符串,长度不超过100。
//定义一个能存放100个字符的数组
char a[100];
//键盘输入字符串
scanf("%s",a);输入完字符串后,我们要开始构建二叉树了,因此,二叉树结点的代码如下:
//结点里面的数据类型都是char(字符型)
typedef char BTDataType;
typedef struct BinaryTreeNode{
BTDataType data; //结点的数据域
struct BinaryTreeNode* left; //结点的左孩子
struct BinaryTreeNode* right;//结点的右孩子
}BTNode;光有结点可不行,咱们要构建的是二叉树,因此,我们还需要一个函数来实现将数组里面的元素拷贝到二叉树中,将这个二叉树还原出来,最后用根节点root来接受返回值,题目还要求我们对这个构建好的二叉树进行中序遍历,因此,在main方法里面的代码如下:
//输入包括1行字符串,长度不超过100。
//定义一个能存放100个字符的数组
char a[100];
//键盘输入字符串
scanf("%s",a);
//定义数组下标i,i从0开始
int i = 0;
//用根节点root来接收返回构建完毕的二叉树
BTNode* root = CreateTree(a,&i);
//对构建好的二叉树进行中序遍历
InOrder(root);OK,大致思路清晰了,接下来我们一步一步讲解~
怎么用数组构建二叉树呢?很简单,就是将数组里面的元素依次拷贝到二叉树结点的数据域中,如果遇到 ' # ' ,说明当前结点为空,返回NULL ,同时下标 i 指向下一个元素 ; 拷贝完当前结点后,继续将数组里面的元素拷贝到当前结点的左孩子和右孩子中,直到读取完整个字符串。
因此,CreateTree函数的代码如下:
BTNode* CreateTree(char* a,int* pi){
//如果遇到 '#' ,下标i指向下一个元素,同时返回NULL
if(a[*pi] == '#'){
(*pi)++;
return NULL;
}
//说明数组里面的元素是有效数据
//开辟一个新结点,用来存放数组里面的元素
BTNode* newNode =(BTNode*) malloc(sizeof(BTNode));
newNode->data = a[(*pi)++];
//将数据拷贝到当前结点后,
//继续将下一个数据拷贝到该结点的左孩子和右孩子中
newNode->left = CreateTree(a,pi);
newNode->right = CreateTree(a, pi);
//返回这个结点
return newNode;
}OK啦,核心代码已经完成,接下来我们对构建好的二叉树进行中序遍历~
中序遍历的代码如下:
void InOrder(BTNode* root){
//如果根节点为空,直接返回
if(root == NULL){
return ;
}
//访问根节点的左子树
InOrder(root->left);
//获取根节点的数据域
printf("%c ",root->data);
//访问根节点的右子树
InOrder(root->right);
}哈哈哈哈,全部的代码我们都完成啦,整体代码如下:
#include <stdio.h>
#include<stdlib.h>
//结点里面的数据类型都是char(字符型)
typedef char BTDataType;
typedef struct BinaryTreeNode{
BTDataType data; //结点的数据域
struct BinaryTreeNode* left; //结点的左孩子
struct BinaryTreeNode* right;//结点的右孩子
}BTNode;
BTNode* CreateTree(char* a,int* pi){
//如果遇到 '#' ,下标i指向下一个元素,同时返回NULL
if(a[*pi] == '#'){
(*pi)++;
return NULL;
}
//说明数组里面的元素是有效数据
//开辟一个新结点,用来存放数组里面的元素
BTNode* newNode =(BTNode*) malloc(sizeof(BTNode));
newNode->data = a[(*pi)++];
//将数据拷贝到当前结点后,
//继续将下一个数据拷贝到该结点的左孩子和右孩子中
newNode->left = CreateTree(a,pi);
newNode->right = CreateTree(a, pi);
//返回这个结点
return newNode;
}
void InOrder(BTNode* root){
//如果根节点为空,直接返回
if(root == NULL){
return ;
}
//访问根节点的左子树
InOrder(root->left);
//获取根节点的数据域
printf("%c ",root->data);
//访问根节点的右子树
InOrder(root->right);
}
int main() {
//输入包括1行字符串,长度不超过100。
//定义一个能存放100个字符的数组
char a[100];
//键盘输入字符串
scanf("%s",a);
//定义数组下标i,i从0开始
int i = 0;
//用根节点root来接收返回构建完毕的二叉树
BTNode* root = CreateTree(a,&i);
//对构建好的二叉树进行中序遍历
InOrder(root);
return 0;
}片尾
今天我们学习了7道二叉树的练习题,说句心里话,第一次我做题的时候,也是迷迷糊糊,磕磕碰碰,但是多做几遍,多画一画图,我相信,小伙伴们都能学会~
求点赞收藏加关注 ! ! !
谢谢大家 ! ! !