文章目录
- 使用Tensorflow解决XOR问题
- 激活函数
- 正向传播和反向传播
- 解决过拟合
- 权重正则化
- Dropout正则化
- 批量正则化 BatchNormal
- 权重初始化
- 残差连接
- 选择优化算法
- 传统梯度更新算法
- 动量算法
- NAG算法
- AdaGrad算法
- RMSProp算法
- Adam算法
- 如何选择优化算法
- 使用tf.keras构建神经网络
- 使用Sequential按层顺序构建模型
- 构建函数式模型
- 构建子类模型
- Fashion-MNIST 分类任务实战
万能近似定理(Universal Approximation theorem)是神经网络的重要理论,其说明了多层网络在足够多的神经元的情况下,是可以拟合任何函数的。Understanding the Universal Approximation Theorem – Towards AI
单层神经网络构造很简单: y ^ = f ( W X ) \hat{y}=f(WX) y^=f(WX)
单层神经网络在分类问题中对线性可分或者近似线性可分的数据有很好的效果,对线性不可分数据则效果不理想,
Minsky在1969年出版的perceptron书中详细的用数学理论证明了单层神经网络无法解决XOR分类问题。
多层神经网络的构造开始复杂起来了: y ^ = f 2 ( W 2 f 1 ( W 1 X ) ) \hat{y}=f_2(W_2f_1(W_1X)) y^=f2(W2f1(W1X))
![![[Pasted image 20240508094043.png]]](https://img-blog.csdnimg.cn/direct/5048d52bfc8640a09597584a0c50c2a7.png)
由于先经过了一次激活函数,在隐藏层的结果是非线性的,对非线性函数再进行激活,其得到的函数构造就会很复杂。
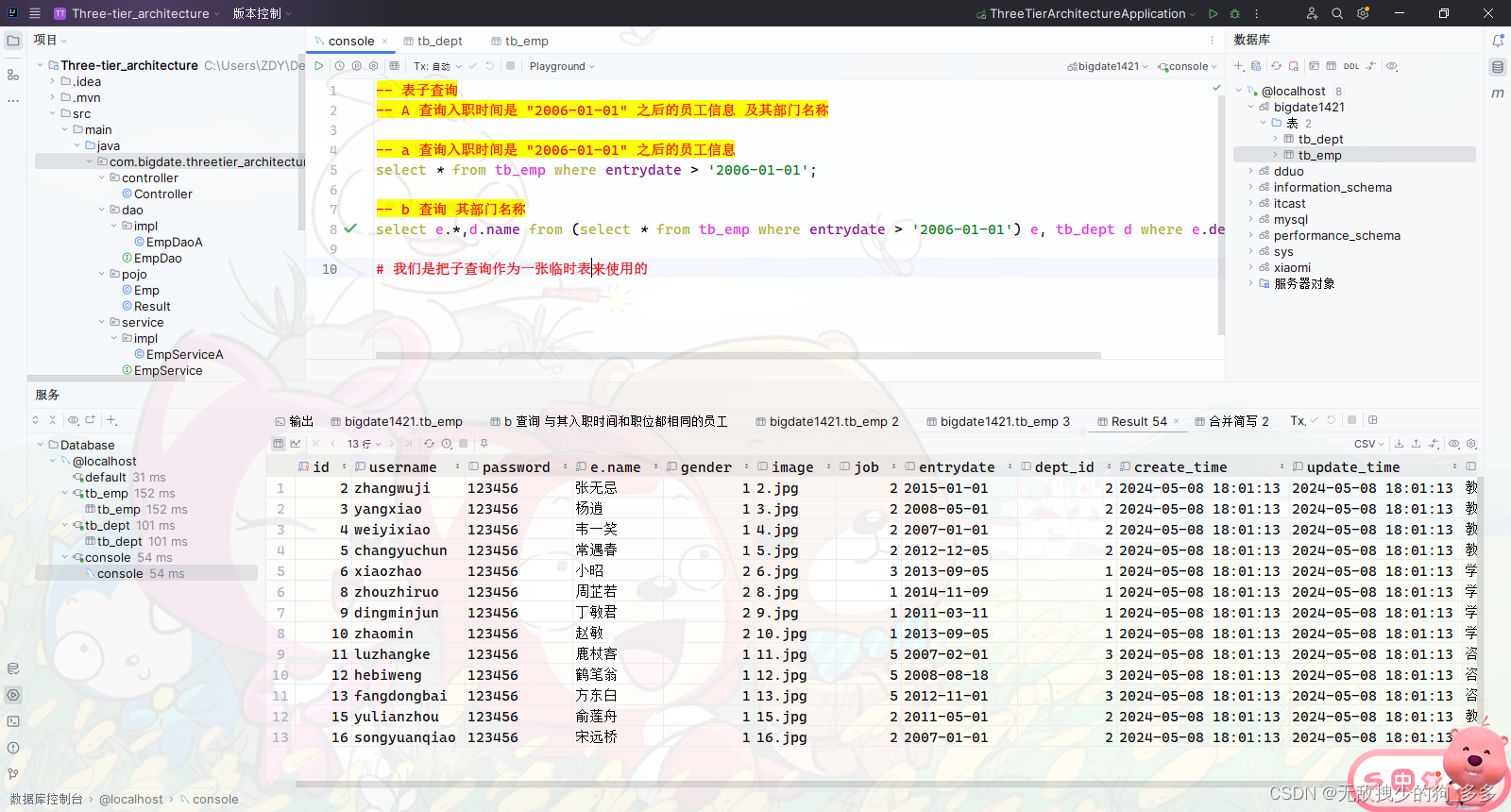
使用Tensorflow解决XOR问题
其中 X O R = O R − A N D XOR=OR - AND XOR=OR−AND,该问题主要是利用 X 1 X_1 X1, X 2 X_2 X2去推测 X O R XOR XOR
| X 1 X_1 X1 | X 2 X_2 X2 | AND | OR | XOR |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 训练代码如下: |
import tensorflow as tf
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib widget
tf.random.set_seed(30)
X = tf.constant([[0.0, 0.0], [0.0, 1.0], [1.0, 0.0], [1.0, 1.0]])
y = tf.constant([0,1,1,0], dtype=tf.float32)
class CustomModel(tf.keras.Model):
def __init__(self):
super(CustomModel, self).__init__()
self.dense_1 = tf.keras.layers.Dense(2, activation='relu')
self.dense_2 = tf.keras.layers.Dense(1)
def call(self, x):
x = self.dense_1(x)
# x = self.dense_2(x)
x = self.dense_2(x)
return x
model = CustomModel()
model.compile(
loss=tf.keras.losses.mse,
optimizer=tf.keras.optimizers.Adam(learning_rate=0.01)
)
history = model.fit(X, y, epochs=1000)
pd.DataFrame(history.history).plot()
由于初始化参数随机设置以及 relu 导致的神经元死亡问题,这里得到的结果不一定稳定,如果需要稳定输出,可以把relu改成leaky_relu,这样神经元死亡不了;
![![[Pasted image 20240508140555.png]]](https://img-blog.csdnimg.cn/direct/c73fb84ccef44e01a695095117d5bc4b.png)
利用matplotlib画图,代码如下:
x_ = tf.linspace(0,1,50)
y_ = tf.linspace(0,1,50)
X_, Y_ = tf.meshgrid(x_,y_)
temp = tf.transpose(tf.concat([tf.reshape(X_, [1,-1]), tf.reshape(Y_, [1,-1])], axis=0), [1, 0])
Z = tf.reshape(model(temp), [50,50])
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.plot_surface(X_,Y_,Z)
plt.show()
可以发现relu类似于把纸张对折了
![![[Pasted image 20240508132840.png]]](https://img-blog.csdnimg.cn/direct/4ef866fdc0c8459bb76db2ab6577e97e.png)
激活函数
激活函数是神经网络的核心,利用激活函数可以把线性函数修正为非线性函数拟合结果,神经网络的激活函数要满足下面三个条件:
- 非线性:为提高模型的学习能力,如果是线性的,无论层多深,都只相当于单层神经网络
- 可微性:在一些点可导
- 单调性:保证模型简单
激活函数一般存储在tf.nn或者tf.keras.activations下
常用的激活函数:
![![[Pasted image 20240508145757.png]]](https://img-blog.csdnimg.cn/direct/548336d03bb94f2aa24f39cbf1aa2bfc.png)
sigmoid:
f
(
x
)
=
1
1
+
e
−
x
f(x) = \frac{1}{1+e^{-x}}
f(x)=1+e−x1
优点:可以把输出映射在0-1区间内, 可以表示概率或者输入的归一化,单调连续,适用于输出层,求导容易;
缺点:具有软饱和性,一旦数据落入饱和区,一阶导数变得接近于0,会导致梯度消失;
softmax:
σ
i
(
z
)
=
e
z
i
∑
e
z
j
\sigma_i(z)=\frac{e^{z_i}}{\sum e^{z_j}}
σi(z)=∑ezjezi
优点:可以处理多分类问题,将数值变成概率;
缺点:计算量比较大;
tanh:
f
(
x
)
=
e
x
−
e
−
x
e
x
+
e
−
x
f(x)=\frac{e^x - e^{-x}}{e^x + e^{-x}}
f(x)=ex+e−xex−e−x
优点:相较于sigmoid,其输出区间为[-1, 1];同时,其斜率更为陡峭,收敛要快于sigmoid
缺点:和sigmoid一样具有软饱和性,会导致梯度消失;
ReLU:
f
(
x
)
=
{
0
x
<
0
x
x
≥
0
\begin{align} f(x) = \begin{cases} 0 \quad &x<0 \\ x \quad &x\geq0 \end{cases} \end{align}
f(x)={0xx<0x≥0
ReLU能够在
x
>
0
x>0
x>0的时候梯度不发生衰减,可以有效的解决梯度消失问题,其选择性的让输入掉入硬饱和区,导致权重无法更新,这种现象叫做“神经元死亡”;
优点:计算简单;
缺点:当大批量输入掉入硬饱和区域,会出现loss不更新现象;
Leaky-ReLU:
f
(
x
)
=
{
a
x
x
<
0
x
x
≥
0
\begin{align} f(x) = \begin{cases} ax \quad &x<0 \\ x \quad &x\geq0 \end{cases} \end{align}
f(x)={axxx<0x≥0
如其名字所言,在
x
<
0
x<0
x<0区域进行倾斜,这里
α
\alpha
α 一般设置为0.5;
优点:解决硬饱和问题;
缺点:不对称问题,会导致拟合函数出现不光滑现象;
softplus:
f
(
x
)
=
l
o
g
(
1
+
e
x
)
f(x)=log(1+e^x)
f(x)=log(1+ex)
优点:非常平滑;
缺点:计算量太大,容易越界;
正向传播和反向传播
正向传播是从输入到输出的过程,而反向传播是从输出到输入的过程,其中反向传播是利用链式法则求导的过程;不知道为啥叫算法,没什么高级的;
解决过拟合
在深度学习中,随着网络层数的增多,一般会出现以下几个问题:
- 增加计算资源的消耗:通过GPU和分布式处理解决;
- 模型容易出现过拟合:多采集数据,使用正则化方式有效避免或者缓解;
- 出现梯度消失或者梯度爆炸:选择合适的激活函数,批量正则化BN;
- 信息丢失:残差连接;
权重正则化
权重正则化采取的方法是对权重添加一个惩罚系数后加入到损失之中,最常见的方式是利用范数的方式: L l = ∣ ∣ w ∣ ∣ l = ∑ ∣ w i ∣ l l L_l=||w||_l=\sqrt[l]{\sum|w_i|^l} Ll=∣∣w∣∣l=l∑∣wi∣l
使用权重正则化最常见的例子就是Lasso回归( L 1 L_1 L1)和Ridge回归( L 2 L_2 L2),当然还有Elastic回归( L 1 L_1 L1, L 2 L_2 L2);
L 1 L_1 L1和 L 2 L_2 L2的区别
- L1减少的是一个常量,L2减少的是权重的固定比例
- L1使权重稀疏,L2使权重平滑
- L1优点是能够获得sparse模型,对于large-scale的问题来说这一点很重要,因为可以减少存储空间
- L2优点是实现简单,能够起到正则化的作用。缺点就是L1的优点:无法获得sparse模型
Dropout正则化
Dropout是2014年论文Dropout: a simple way to prevent neural networks from overfitting提出的一种方法,其通过在每次训练的时候随机丢掉一部分神经元的方式来训练模型,这样输入的特征都可能被丢掉,所以模型不会依赖于任何一个输入特征,也就是说不会给任何一个神经元过大的权重,网络模型对神经元特定的权重不会那么敏感,反过来提升了模型的泛化能力,不容易过拟合;
在测试模型的时候,会等比例缩小模型的权重以适应丢掉的神经元带来的放大效果,即乘以 Dropout rate
在什么情况下使用Dropout:
- 通常
Dropout rate控制在20%-50%比较好,太低起不到效果,太高会导致模型欠拟合 - 在大的网络模型上应用,当Dropout用在较大的模型时,更有可能提升效果,应为此时模型有更多的机会学习到多种独立表征;
- 在输入层和隐藏层都使用Dropout,对于不同的层,设置的
Dropout rate不同,一般来说,对神经元较少的层,会将Dropout rate设置为0或者接近于0的数,对于神经元多的层,会将Dropout rate设置得较大,如0.5或者更大; - 增加学习率和冲量,把学习率扩大10-100倍,冲量调高的0.9-0.99;
- 限制网络模型的权重,大的学习速率往往导致比较大的权重值,对网络的权重值做最大范数的正则化,被证明可以提升模型性能;
批量正则化 BatchNormal
数据归一化,数据标准化都是对输入数据而言的,在实际训练中由于神经元的权重计算仍然会出现隐藏层各个神经元的数值分布不均匀,导致梯度消失或者不起作用的情况。例如:如果数据分布在两侧,采用sigmoid或者tanh激活时,两侧的导数近似于0,这就会导致梯度消失的情况。
BatchNormal通过修改Batch数据的均值和方差来解决由于数据不均匀导致梯度消失这一问题,可以让调试超参数更加简单,在提高训练模型效率的同时,让神经网络模型泛化能力更高;
首先计算Batch数据的均值和方差:
μ
=
1
m
∑
x
i
σ
2
=
1
m
∑
(
x
i
−
μ
)
2
\mu = \frac{1}{m}\sum x_i \quad \sigma^2 = \frac{1}{m}\sum (x_i-\mu)^2
μ=m1∑xiσ2=m1∑(xi−μ)2
再对Batch数据进行放缩:
x
^
i
=
x
i
−
μ
σ
2
+
ϵ
\hat{x}_i=\frac{x_i-\mu}{\sqrt{\sigma^2 + \epsilon}}
x^i=σ2+ϵxi−μ
最后对Batch数据进行反标准化:
y
i
=
γ
x
^
i
+
β
=
NB
γ
,
β
(
x
i
)
y_i=\gamma \hat{x}_i + \beta=\text{NB}_{\gamma,\beta}(x_i)
yi=γx^i+β=NBγ,β(xi)
这里
ϵ
\epsilon
ϵ 是自定义的一个很小的值,
γ
\gamma
γ 和
β
\beta
β 类似于权重参数,是可以学习的,也就是说,一个BatchNormal层是有两个学习权重的;
BN作用在非线性映射前,也就是激活函数前面,一般在神经网络训练中遇到收敛速度很慢,或梯度爆炸等无法训练的情况时使用,在一般情况下,也可以使用BN来加快模型训练速度,提高模型精度,进而提高训练模型的效率,BN的具体功能如下:
- 可以使用比较大的学习率,让训练速度加倍,因为这个算法收敛很快;
- 不用再去理会过拟合中的Dropout,L2正则化项参数的选择问题,采用BN后,可以移除这两项正则化方法,或者使用更小参数的L2正则约束参数;
- 不需要使用局部响应归一化层LRN(这个层基本弃用了);
- 可以把训练速度彻底打乱;
权重初始化
不同的初始值,会导致模型收敛到不同的极值点,这里的XOR问题应该已经说明了问题,常见的模型权重初始化有零值初始化,随机初始化,均匀分布初始化,正态分布初始化,正交分布初始化等等,一般来说采用正态分布或者均匀分布的初始值,经过实践证明,这能带来更好的效果;
残差连接
残差连接的思想很简单:
F
(
x
)
=
f
(
x
)
+
x
F(x) = f(x)+x
F(x)=f(x)+x
从信息论的角度来看,由于数据处理不等式的存在,在正向传播的过程中,由于层数的加深,每一层所包含的信息准层减少,而残差连接保证了后一层是前一层的信息加上处理后的信息;
选择优化算法
传统梯度更新算法
传统梯度更新算法的基本思想是:设定一个学习率
λ
\lambda
λ,参数沿梯度反向移动:
θ
←
θ
−
λ
g
\theta \leftarrow \theta - \lambda g
θ←θ−λg
优点:算法简洁,当学习率设置恰当时,可以收敛到全局最优点;
缺点:对超参数学习率过于敏感,过小导致收敛速度过慢,过大将越过极值点;由于学习率不发生变化,容易卡在鞍点;在平坦区域,由于梯度接近于0,容易提前结束迭代;
动量算法
顾名思义,利用上一次计算到的梯度加权结合本次计算到的梯度;
![![[Pasted image 20240508195259.png]]](https://img-blog.csdnimg.cn/direct/d3dd68ca953648f4ab0c10bc6532660e.png)
用公式表述过程如下:
v
t
=
a
v
t
−
1
−
λ
g
t
θ
t
+
1
←
θ
t
+
v
t
v_t = av_{t-1}-\lambda g_t \quad \theta_{t+1} \leftarrow \theta_t + v_t
vt=avt−1−λgtθt+1←θt+vt
动量有一个明显的优点是:可以冲!

假设每个点的梯度相似,根据等比数列可以得到:
v
k
=
λ
g
1
−
a
v_k=\frac{\lambda g}{1-a}
vk=1−aλg
当
a
a
a 等于0.5,0.9时,其速度是梯度下降法的2倍和10倍;
NAG算法
NAG和动量的区别在于NAG计算两次梯度,一次超前梯度,一次原来梯度,将两次梯度合并;
![![[Pasted image 20240508195234.png]]](https://img-blog.csdnimg.cn/direct/341f96587f4144c3ba4fb7f536b67f91.png)
NAG 是 动量算法 的一种改进算法,可以防止大幅震荡,不会错过最小值,对参数更新更为敏感;
AdaGrad算法
AdaGrad 算法 是自适应算法,可以从梯度方向及学习率两个维度进行优化;
其计算方法为:
r
←
r
+
g
^
⊙
g
^
Δ
θ
←
−
λ
δ
+
r
⊙
g
^
θ
←
θ
+
Δ
θ
r \leftarrow r + \hat{g} \odot \hat{g} \quad\quad \Delta \theta \leftarrow -\frac{\lambda}{\delta + \sqrt{r}} \odot \hat{g} \quad\quad \theta \leftarrow \theta + \Delta \theta
r←r+g^⊙g^Δθ←−δ+rλ⊙g^θ←θ+Δθ
随着训练步数的增长,
r
r
r 的值越来越大,AdaGrad 算法的学习率会越来越小,这样就不容易错过极值点;这里的
δ
\delta
δ 一般取一个较小的值,如
1
0
−
7
10^{-7}
10−7,该参数避免分母为0;
RMSProp算法
RMSProp算法 也是 自适应算法, 在AdaGrad算法的基础上做了修改,可以使优化器在非凸背景下效果更好,RMSProp采用指数加权的移动平均代替梯度平方和;
其计算方法为:
r
←
ρ
r
+
(
1
−
ρ
)
g
^
⊙
g
^
Δ
θ
←
−
λ
δ
+
r
⊙
g
^
θ
←
θ
+
Δ
θ
r \leftarrow \rho r + (1-\rho) \hat{g} \odot \hat{g} \quad\quad \Delta \theta \leftarrow -\frac{\lambda}{\delta + \sqrt{r}} \odot \hat{g} \quad\quad \theta \leftarrow \theta + \Delta \theta
r←ρr+(1−ρ)g^⊙g^Δθ←−δ+rλ⊙g^θ←θ+Δθ
由于
ρ
\rho
ρ 的限制,
r
r
r 有衰减项,不会无限增长,但是RMSProp相较于AdaGrad多了一个
ρ
\rho
ρ,这里的
δ
\delta
δ 一般取一个较小的值,如
1
0
−
7
10^{-7}
10−7,该参数避免分母为0;
Adam算法
Adam(Adaptive Moment Estimation) 算法 又叫自适应矩估计算法,其本质是带有动量项的RMSProp;利用梯度的一阶矩估计和二阶矩估计来调整学习率;
矩估计计算如下: s ← ρ 1 s + ( 1 − ρ 1 ) g ^ r ← ρ 2 r + ( 1 − ρ 2 ) g ^ ⊙ g ^ s \leftarrow \rho_1s+(1-\rho_1)\hat{g} \quad r \leftarrow \rho_2r+(1-\rho_2)\hat{g} \odot \hat{g} \quad s←ρ1s+(1−ρ1)g^r←ρ2r+(1−ρ2)g^⊙g^
修正矩估计,这里
t
t
t 是指时间步,第
t
t
t 次梯度更新:
s
^
=
s
1
−
ρ
1
t
r
^
=
r
1
−
ρ
2
t
\hat{s} = \frac{s}{1-\rho_1^t} \quad \hat{r} = \frac{r}{1-\rho_2^t}
s^=1−ρ1tsr^=1−ρ2tr
更新梯度:
r
←
ρ
r
+
(
1
−
ρ
)
g
^
⊙
g
^
Δ
θ
←
−
λ
s
^
δ
+
r
^
θ
←
θ
+
Δ
θ
r \leftarrow \rho r + (1-\rho) \hat{g} \odot \hat{g} \quad\quad \Delta \theta \leftarrow -\lambda \frac{\hat{s}}{\delta + \sqrt{\hat{r}}} \quad\quad \theta \leftarrow \theta + \Delta \theta
r←ρr+(1−ρ)g^⊙g^Δθ←−λδ+r^s^θ←θ+Δθ
这里需要给的超参数有,学习率 λ \lambda λ , ρ 1 \rho_1 ρ1, ρ 2 \rho_2 ρ2, ρ \rho ρ;初始化后 s s s, r r r, t t t 都等于0 ;这里的 δ \delta δ 一般取一个较小的值,如 1 0 − 7 10^{-7} 10−7,该参数避免分母为0;
如何选择优化算法
综合考虑算法,早期阶段SGD对参数的调整和初始化非常敏感,经验算法:先使用Adam优化算法进行训练,既能大幅节省时间,又能避免初始化和参数调整问题,用Adam算法调整好后,再使用SGD+动量优化算法,以达到最佳性能;
使用tf.keras构建神经网络
Keras 是一个主要由 Python 语言开发的开源神经网络计算库,最初由 François Chollet 编写,它被设计为高度模块化和易扩展的高层神经网络接口,使得用户可以不需要过多的专业知识就可以简洁、快速地完成模型的搭建与训练。Keras 库分为前端和后端,其中后端可以基于现有的深度学习架构实现,如TensorFlow、Theano、CNTK等。 TensorFlow 与 Keras 存在既竞争又合作的关系,甚至连 Keras 创始人都在Google 工作。早在2015年11月,TensorFlow被加入Keras后端支持。从2017年开始,Keras的大部分组件被整合到TensorFlow架构中。在2019年6月发布TensorFlow 2版本时,Keras 被指定为TensorFlow官方高级 API,用于快速简单的模型设计和训练。现在只能使用 Keras的接口来完成TensorFlow层方式的模型搭建与训练。在TensorFlow中,Keras被实现在tf.keras模块中。下文如无特别说明,Keras均指代tf.keras实现,而不是以往的 Keras实现。
| 主要模块 | 功能概述 |
|---|---|
| activations | 内置的激活函数 |
| applications | 预先训练权重的罐装架构Keras应用程序 |
| Callbacks | 在模型训练期间的某些时刻被调用的实用程序 |
| Constraints | 约束模块,对权重施加约束的函数 |
| datasets | tf.keras数据集模块,包括boston_housing,cifar10,fashion_mnist,imdb ,mnist,reuters |
| estimator | Keras估计量API |
| initializers | 初始序列化/反序列化模块 |
| layers | Keras层API,包括卷积层、全连接层、池化层、Embedding层等 |
| losses | 内置损失函数 |
| metircs | 内置度量函数 |
| mixed_precision | 混合精度模块 |
| models | 模型克隆的代码,以及与模型相关的API |
| optimizers | 内置的优化器模块 |
| preprocessing | Keras数据的预处理模块 |
| regularizers | 内置的正则模块 |
使用Sequential按层顺序构建模型
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
model = tf.keras.Sequential()
model.add(layers.Dense(32, activation='relu'))
model.add(layers.Dense(32, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
model.compile(
optimizer=tf.keras.optimizers.Adam(0.001),
loss=tf.keras.losses.categorical_crossentropy,
metrics=[tf.keras.metrics.categorical_accuracy]
)
构建函数式模型
import tensorflow as tf
from tensorflow import keras
inputs = tf.keras.Input(shape=(3,))
input = keras.layers.Input(shape=[], name="input")
hidden1 = keras.layers.Dense(60, activation="relu")(input)
hidden2 = keras.layers.Dense(60, activation="relu")(input)
concat = keras.layers.concatenate([hidden1, hidden2])
output = keras.layers.Dense(1, name="output")(concat)
model = keras.Model(inputs=[input], outputs=[output])
构建子类模型
import tensorflow as tf
class MyModel(tf.keras.Model):
def __init__(self):
super(MyModel, self).__init__()
self.dense1 = tf.keras.layers.Dense(4, activation=tf.nn.relu)
self.dense2 = tf.keras.layers.Dense(5, activation=tf.nn.softmax)
def call(self, inputs):
x = self.dense1(inputs)
return self.dense2(x)
model = MyModel()
Fashion-MNIST 分类任务实战
Fashion-MNIST 是一个图片分类任务,其输入是一张张图片,而输出是0-9个类别;
![![[Pasted image 20240508204659.png]]](https://img-blog.csdnimg.cn/direct/64576c8d87a2434e904ffa25ec5fb8fd.png)
导入数据并进行数据预处理;
import tensorflow as tf
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
(x_train, y_train), (x_test, y_test) = (x_train/255.0, y_train), (x_test/255.0, y_test)
# x_train.shape, y_train.shape, x_test.shape, y_test.shape
# ((60000, 28, 28), (60000,), (10000, 28, 28), (10000,))
构建模型,这里使用class的方式构建;
class CustomModel(tf.keras.Model):
def __init__(self):
super(CustomModel, self).__init__()
self.flatten = tf.keras.layers.Flatten()
self.dense_1 = tf.keras.layers.Dense(512, activation='relu')
self.dense_2 = tf.keras.layers.Dense(128, activation='relu')
self.dense_3 = tf.keras.layers.Dense(32, activation='relu')
self.dense_4 = tf.keras.layers.Dense(10, activation='softmax')
def call(self, x):
x = self.flatten(x)
x = self.dense_1(x)
x = self.dense_2(x)
x = self.dense_3(x)
x = self.dense_4(x)
return x
model = CustomModel()
model.compile(
loss=tf.keras.losses.sparse_categorical_crossentropy,
optimizer=tf.keras.optimizers.Adam(learning_rate=0.001),
metrics=[tf.keras.metrics.sparse_categorical_accuracy]
)
训练模型并使用tensorboard可视化
def get_logdir():
root_logdir = os.path.join(os.curdir, "my_logs")
run_id = time.strftime("run_%Y%m%d-%H%M%S")
return os.path.join(root_logdir, run_id)
logdir = get_logdir()
tensorboard_cb = keras.callbacks.TensorBoard(logdir)
history = se_model.fit(x_train, y_train, epochs=10,callbacks=[tensorboard_cb])
tensorboard --logdir="文件目录" 打开tensorboard
最后可以得到分类准确率在90%