Abstract
谣言在社交网络中快速传播,可能严重损害我们的社会。在本文中,我们提出了一种基于整数线性规划(ILP)的数学规划公式,通过阻止建模为线性阈值模型的复杂社交网络中的节点子集(称为阻止者)来最大程度地减少谣言传播。我们还提出了一种改进的方法,可以减少计算量来解决 top-k 阻塞问题,并正式证明其性能仍然是最优的。然后,评估所提出的方法在四个不同网络中遏制谣言传播的有效性,并将其性能与基于贪婪的方法和两种基于中心性的方法进行比较。实验分析表明,基于ILP的方法优于其他三种方法,并且适用于大规模网络。
索引术语——阻塞节点、整数线性规划(ILP)、线性阈值模型(LTM)、谣言传播。
I. INTRODUCTION
许多网络系统都涉及由代理或个人之间的相互影响驱动的传播现象。例如,在社交网络中,人们可能会受到朋友的影响而采取一项创新、传播一条信息或参与一项政治活动。在基础设施网络中,一些组件的故障可能会导致大规模的临时停电,甚至导致灾难性故障。在大量人类或动物群体中,流行病在个体之间迅速传播。进入21世纪以来,随着通信技术的进步,在线社交网站为人们提供了新的、更简单的方式来分享信息、交流思想,甚至采用创新。影响传播分析已成为跨越计算机科学、社会学、控制论等多个学科的热门研究课题。此类研究可能为理解复杂网络中的影响动力学机制和开发预测网络影响的技术提供新的关键。个人的行为,以防止或控制不良行为。
尽管网络系统中的传播是一种复杂的现象,但已经有一些成功的尝试用数学模型来描述它。 Kempe 等人提出的两种广泛采用的离散时间扩散模型。 [1] 是线性阈值模型(LTM)和独立级联模型(ICM),它们考虑有向图,其中节点表示用户或个人,弧表示两个用户之间的关系。在某个时间,每个节点可以是活动的,也可以是不活动的。活跃状态意味着该节点采用了创新,否则处于非活跃状态。最初,所有节点均处于非活动状态。在时间 0,网络中的一些节点被激活以根据模型动态开始传播。
受到复杂网络中不同实际应用的推动,包括谣言传播抑制[2]、[3]、[4]、[5]、[6]、[7]、病毒式营销中的广告[8]、[9]、[ 10]、[11]等。Kempe 等人。 [1]介绍了迄今为止该框架中研究最广泛的问题——影响最大化(IM)问题。 IM 问题在于识别早期采用者的一小部分(所谓的种子集)以实现最大影响力传播。他们将问题形式化为组合优化问题,并证明它对于 ICM 和 LTM 模型都是 NP 困难的。为了解决 IM 问题,提出了一种贪婪方法,该方法可以实现有保证的近似解(尽管计算成本很高)。 IM 问题的理论难度促使众多研究人员为其解决方案设计可行的算法。文献中记录的方法可以分为四类:1)具有可证明保证的近似算法[12],[13],[14],[15],[16]; 2)基于社区的算法[17]; 3)启发式方法[18],[19],[20]; 4)元启发法[21]。
IM 问题旨在最大限度地传播有价值的信息等所需内容。不良或破坏性内容,例如基础设施故障和虚假新闻,也可能在网络系统中传播,并可能对人造系统或我们的社会产生灾难性影响。例如,“白宫两次爆炸,奥巴马受伤”的假推文造成美国股市不稳定,在谣言被澄清之前短时间内损失了100亿美元[22]。显然,研究如何遏制或控制不良内容的传播具有社会和经济意义。
这项工作解决了控制复杂社交网络中谣言传播的问题。通常,谣言控制策略分为两种类型:1)抗衡策略和2)网络破坏策略。
A. Counterbalance Strategy
制衡策略试图通过传播反谣言或真相来抵消谣言的负面影响,使两种相反的信息相互争斗。 [3]、[4]、[23] 和 [24] 中通过扩展 LTM 来描述谣言和事实之间的竞争性传播动态来最小化谣言传播。 [23]和[24]中涉及的扩散模型被假设是渐进的,即一旦用户采用一种类型的信息,它将忽略任何其他信息。然而,杨等人。 [4]让首先采纳谣言的个体重新考虑自己的信念,这是一种更符合真实个体行为的机制。 [25]和[26]中还使用 ICM 的不同扩展来研究谣言控制问题。最近,Manouchehri 等人。 [27]通过采用竞争性 ICM 解决了上述问题的扩展版本,即所谓的时间谣言阻止问题。
B. Disruption Strategy
网络破坏策略可以通过从网络中删除(或阻止)一些关键节点/边缘来完成,尝试断开不活动节点与活动节点的连接,以抑制谣言传播。 Kimura 等人考虑基于边缘的谣言遏制问题。 [28] 和哈利勒等人。 [29]使用贪心算法分别在ICM和LTM的框架中搜索近似解。该问题的目标函数在[30]中被证明对于 ICM 是非子模的。幸运的是,作者提出了子模上限和下限,以便他们可以应用三明治算法。 [31] 中提出了基于 GPU 的方法来控制网络流行病的传播,同时考虑了基于边缘和基于节点的 LTM 方案。 Nandi 和 Medal [32] 提出了几种删除链接以抑制感染传播的方法,这些方法也可以用于抑制谣言传播。梅迪亚等人。 [33]通过基于子模性的近似算法解决了链接删除的影响限制问题。
在在线社交平台中阻止用户可能是指拒绝某些用户的访问,使他们无法看到和传播谣言[34]。从网络角度来看,阻止节点被视为从网络中删除该节点及其与其他节点的所有连接,从而确保中断从该节点到其他节点的路径。 [35]、[36]和[37]中考虑了这种基于节点的方案。基于节点的谣言遏制问题旨在识别最有效的节点(所谓的阻止者),在[35]中被形式化为优化问题,并通过自然贪婪近似解决方法。严等人。 [36]提出了一种两阶段贪婪启发式方法,包括为一般网络生成候选者和选择前k个阻塞者,以及考虑ICM作为扩散模型的树网络动态规划方法。萨哈等人。 [37]考虑了流行病模型,通过去除一些关键节点或边,将感染最小化问题转化为网络谱半径最小化问题。与上述策略不同,[38]中提出了一种组解散方案来解决由聊天组内的回声室效应引起的错误信息传播最小化问题。
我们注意到节点的删除(或块)涉及边缘的删除。然而,基于边缘的谣言遏制问题的解决方案不能直接用于基于节点的谣言遏制问题。此外,在群体网络中,块节点比块链接更合理、更有趣。因此,在这项工作中,我们采用阻塞节点的选项来遏制谣言传播。寻找 top-k 阻断剂的问题具有组合性质,并且通常需要详尽的搜索。上述大多数结果都试图通过贪婪方法来解决这个问题,但对于非常大的网络来说,这种方法不能很好地扩展。此外,top-k 阻塞问题既不是子模问题也不是超模问题,这意味着贪婪方法没有近似保证。除了贪婪方法之外,本文旨在提出一种提供最佳解决方案的代数方法,并使其可扩展用于大型网络。流程图如图1所示。
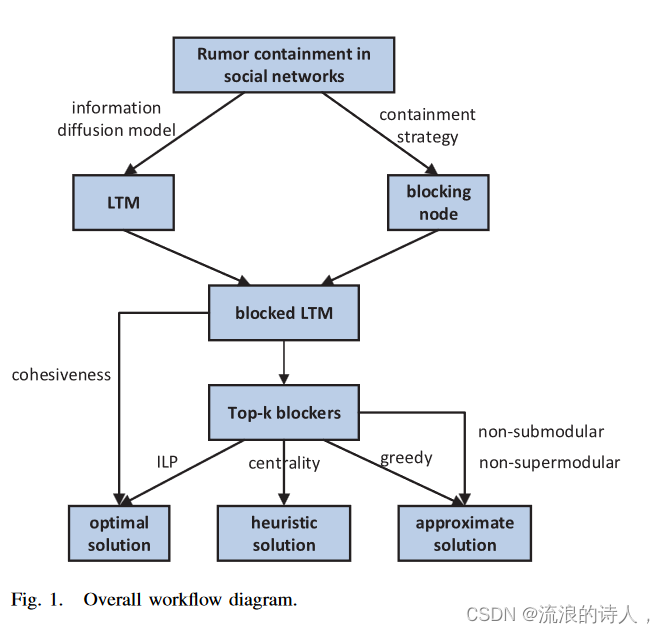
图 1. 总体流程图。
本文认为 LTM 在数学上描述了社交网络中谣言的传播动态,因为阈值模型相对适合描述集体行为。从网络的角度来看,为了识别有效的阻塞者,我们不是删除它们及其连接,而是为它们分配大于 1 的阈值。这种策略的工作原理与删除节点相同,因为 LTM 标准化了影响权重从邻居到1。然后,任何具有阈值的节点大于 1 则永远保持不活动状态。我们的贡献是多方面的。
1)定义了一种特殊的LTM,称为阻塞线性阈值网络,其中某些节点的阈值大于1,表示节点被阻塞。
2)我们表明,在线性阈值网络中,单调性对于topk阻塞问题的目标函数成立,但是,子模性和超模性则不然。
3)考虑到阻塞线性阈值网络,top-k阻塞问题首先被形式化为非线性规划(NLP)问题。然后提出非线性公式的线性化,以便可以通过解决整数线性规划(ILP)问题来识别最佳的前k个阻断剂。通过证明整个网络的演化可以等效地由其活动子网络表示,我们可以进一步降低线性化规划的复杂性。
4)我们将数学规划方法与两种基于中心性的方法和基于贪婪的方法进行比较,以衡量四个不同网络中谣言遏制的有效性。
本文的结构如下。第二节首先回顾了 LTM,然后讨论了阻塞节点对网络演化的影响。第三节定义并分析了 top-k 拦截器问题。第四节展示了通过解决 NLP 问题来解决 top-k 阻塞问题的最佳解决方案,该问题可以进一步线性化为 ILP 问题。第五节介绍了基于贪婪的方法和两种基于中心性的方法。第六节展示了对我们的数学规划方法和其他三种启发式方法的一系列实验评估。第七节总结了本文。
II. LINEAR THRESHOLD NETWORKS
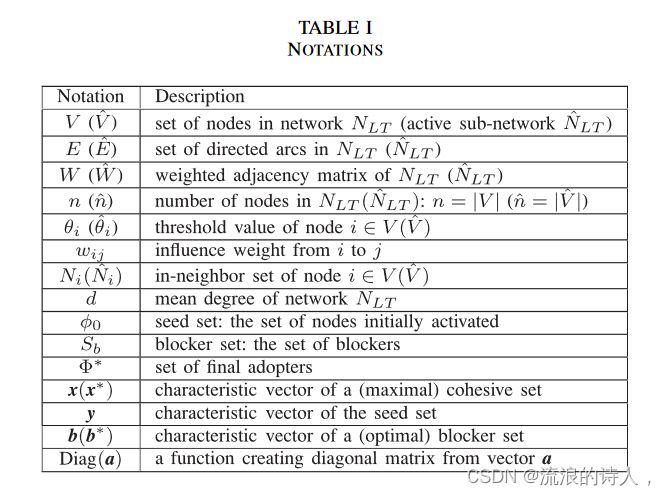
我们首先介绍 LTM 来解释影响力或信息如何在社交网络中传播。表一列出了本文中的一些符号和解释。
A. Linear Threshold Network
线性阈值网络 NLT 是一个四元组 (V, E,θ,w),其中:
1) V ={1, 2,...,n} 表示网络中节点的集合;
2) E ⊆ V × V 表示一组有向弧,如果从节点 i 到节点 j 存在一条弧,则称 (i, j) ∈ E;
3) 函数 θ : V → (0, 1] 是一个映射,为每个节点 i ∈ V 分配一个阈值 θi ∈ (0, 1];
4) 函数 w : V × V → [0, 1] 是一个映射为每个弧 (i, j) ε E 分配影响权重 wij ∈ (0, 1] 的映射,使得 wij = 0if(i, j)/ ε E 且对于所有 j ∈ V Σ i∈V wij = 1。我们假设弧(i, i),即自循环,仅对于源节点(没有内邻居)才可能,在这种情况下,它们的权重必须为1以确保 Σ i∈V wij = 1.
网络 NLT 中的每个节点 i 代表一个个体。它的阈值 θi 表示该节点表现得像其邻居的趋势[1]。节点 i ∈ V 的近邻集定义为 Ni ={j|(j, i) ε E}。Arc(i, j) 表示节点 i 可以影响节点 j。我们用 = Diag([θ1,θ2,...,θn]) 表示网络的阈值矩阵:其对角线元素是节点的阈值,所有非对角线元素均为空。令 W ∈ [0, 1]n×n 表示网络的加权邻接矩阵,其中 W(i, j) = wij。
每个节点可以是不活动的,也可以是活动的。最初,所有节点均处于非活动状态。令 φ0 ⊆ V 为种子集,代表在步骤 t = 0 时激活的一组节点。扩散过程源于这些种子,它们试图逐步影响其他节点。让 φt 表示在步骤 t 激活的节点集。在步骤 t 处处于活动状态的节点集,即在 [0, t] 中的任何步骤处已激活的节点,表示为 t = ⋃t k=0 φk。根据定义,我们有 0 = φ0。
在每个步骤 t = 1, 2,...,如果步骤 t − 1 处的活动邻居的影响权重总和超过其阈值 θi,则非活动节点 i 会将其状态更改为活动状态,即
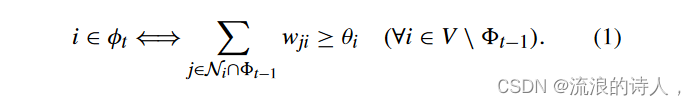
激活按照(1)以渐进的方式传播,即不考虑去激活过程,并且活动节点从不切换其状态。因此,网络将在某些步骤中达到稳定状态,所有节点都不会切换其状态。它的特征是最终采用者的集合,定义为 ∗(NLT ,φ0) = ⋃∞ k=0 φk。
通过模拟上述演化过程,可以得到最终采用者集合,直到达到停止标准,即不再激活不活跃节点,参见附录中的算法A1。该过程的计算时间复杂度为 O(nd),其中 n 表示节点数量,d 表示底层网络的平均度。
B. Properties of Linear Threshold Network
在这一部分中,我们没有模拟网络的演化过程来确定稳态,而是展示了一个线性的基于内聚性概念的代数方法确定其。
1) 内聚性:内聚集最初由 Acemoglu 等人在未加权线性阈值网络中定义。 [8]。我们在下面将其定义推广到加权网络。
定义 1:如果对于所有 i ∈ X,子集 X ⊆ V 被称为内聚集
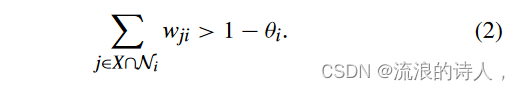
我们可以从(2)中得知一个有趣的性质:如果 φ0 ∩X =∅,那么对于所有 t ≥ 0,φt ∩ X =∅。也就是说,如果X中不存在种子节点,那么X中的所有节点将始终保持不活动状态。此外,内聚集的并集也是内聚的。
引理1[8]:给定一个LTM网络NLT=(V,E,θ,w)和种子集φ0⊆V,令M⊆V\φ0是V\φ0中包含的最大内聚集。最终采用者集是
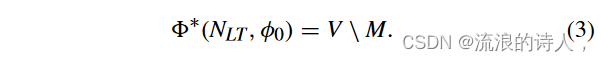
2) *(NLT ,φ0) 的代数表征: 定义2:给定一个集合X ⊆ V,其特征向量x ∈{0, 1}n 定义为xi = 1ifi ∈ X;否则 xi = 0,即

[9]中提出的内聚集的充分必要条件也可以推广到加权网络。引理 2 [9]: AsetX ⊆ V 是内聚的当且仅当其特征向量 x 满足
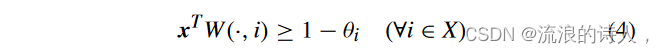
其中 W(·, i) 是加权邻接矩阵 W 的第 i 列。
引理 1 为我们提供了一种直接的方法来计算最终采用者的集合,从而避免确定详细的演化过程。然后,基于引理1和2,命题1提出了稳态的代数表征。注意,在本文的线性或非线性程序中,x表示决策变量向量(即内聚集的特征向量) )而x*表示最优解(即最大内聚集的特征向量)。
命题1[9]:给定一个有n个节点的LTM网络NLT=(V,E,θ,w),设y为种子集φ0⊆V的特征向量。V\φ0中包含的最大内聚集M有特征向量 x*,是以下 ILP 问题的最优解:
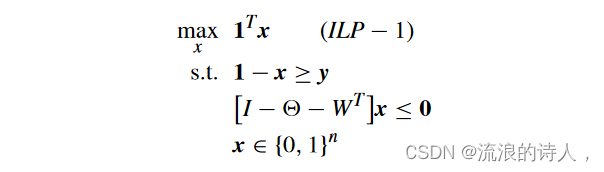
其中 I 是 n × n 单位矩阵。最终采用者的集合是 ∗(NLT ,φ0) ={i ∈ V|x∗ i = 0}。
注:加权邻接矩阵W(如第二节中定义)与[9]中采用的不同(letuscallitW),其中不允许自循环,因此所有对角线元素均为空。使用[9]中的定义,命题1仅适用于没有源节点的网络。然而,使用我们对 W 的定义,当存在源节点时,命题 1 也成立。下面,我们展示一个使用 (ILP-1) 分别使用两个不同的加权邻接矩阵 W 和 ̄ W 来计算最终采用者集合的示例。
示例1:考虑图2中的线性阈值网络NLT,其具有六个节点,其中节点1和6是源节点。每个节点旁边的值是阈值,每个弧旁边的值是相关的影响权重。假设φ0={1}。使用 ̄ W 求解整数线性规划 (ILP-1) 将返回最终采用者集合 ∗(NLT ,φ0) ={1, 2, 3, 4, 5, 6}。相反,如果我们使用 W,我们可以获得 ∗(NLT ,φ0) ={1, 2}。这与算法A1得到的结果一致,算法A1也输出*(NLT,φ0)={1, 2}。
C. Network Evolution With Blocking of Nodes
一组阻塞节点 Sb ⊆ V \ φ0 在文献中被称为阻塞器集。在这一部分中,我们讨论阻塞节点对网络演化的影响。
给定 LTMNLT = (V, E,θ,w)、种子集 φ0 ⊆ V 和阻止者集 Sb ⊆ V \ φ0,我们用 ∗(NLT ,φ0, Sb) 表示具有阻止者集 Sb 的最终采用者集。在有阻塞的网络中,激活规则(1)仅适用于未被阻塞的节点。我们可以通过稍微修改算法 A1 来计算 ∗(NLT ,φ0, Sb):在第 3 行中初始化 c = V \ (φ0 ∪ Sb)。
给定 LTM NLT = (V, E,θ,w) 和 Sb,我们可以定义等效的阻塞线性阈值网络 N′ LT = B(NLT , Sb) = (V, E,θ′, w) 其中 θ ′是为每个节点 i ∈ V 分配阈值 θ ′ i 的映射,使得
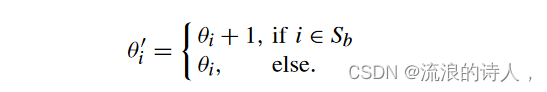
具有阻塞器集 Sb 的 LTM NLT 生成阻塞线性阈值网络 N′ LT ,这是一种特殊的 LTM,其中某些阈值大于 1。阻塞器是 N′ LT 中 θ ′ i >1 的那些节点。标准LTM NLT 中节点的激活规则仍然适用于N' LT 。 LTM 假设来自邻居的影响权重之和等于 1。根据(1),θ ′ i > 1 的不活动节点永远不会被激活。事实证明,这个结果与阻止节点的目标是一致的,即阻止它被激活并进而触发其不活动的追随者。
下面我们将证明,LTM NLT 中具有阻止者集的最终采用者集合等价于相应的阻止 LTM N' LT 中的最终采用者集合。
令 φt(NLT , φ0, Sb) 和 φt(N' LT , φ0) 分别表示网络 NLT 中在步骤 t 激活的节点集合,其中具有阻塞集合 Sb 和相应的阻塞 LTM N' LT
命题 2:给定一个 LTM 网络 NLT = (V, E,θ,w),种子集 φ0 ⊆ V,阻塞集 Sb ⊆ V \φ0,带有阻塞集 Sb 的网络 NLT 的演化过程等价于其分块线性阈值网络 N′ LT = B(NLT , Sb) = (V, E,θ′, w),即 φt(NLT ,φ0, Sb) = φt(N′ LT ,φ0)
证明:对于 t = 0,这两个集合根据定义是相同的。我们可以通过证明对于任何 t ≥ 1,它保持 φt(NLT ,φ0, Sb) = φt(N′ LT ,φ0) 来证明结果。
我们从 t = 1 开始,对于任意节点 i,我们有 i ∈ φ1(NLT ,φ0, Sb) 当且仅当满足 Σ j∈φ0∩Ni wji ≥ θi,即 Σ j∈φ0∩Ni wji ≥ θ ′ i 因为i / ε Sb 和 θ ′ i = θi。这意味着 i ε φ1(N′ LT ,φ0)。然后,我们有 φ1(NLT ,φ0, Sb) = φ1(N′ LT ,φ0)。该语句对于步骤 t = 2 也成立,然后通过递归,对于任何 t > 2,它都成立 φt(NLT ,φ0, Sb) = φt(N′ LT ,φ0)。
令 ∗(N′ LT ,φ0) 表示给定 φ0 的 N′ LT 中的稳态。我们有 ∗(N′ LT ,φ0) = ⋃∞ k=0 φt(N′ LT ,φ0)。那么,由命题2我们可以得到如下结果。
推论 1:给定种子集 φ0 ⊆ V,LTM NLT = (V, E,θ,w) 中具有阻止集 Sb ⊆ V\ 的最终采用者集合与 N′ LT = 中的最终采用者集合相同B(NLT , Sb) = (V, E,θ′, w),即*(NLT ,φ0, Sb) = *(N′ LT ,φ0)。
下面我们举一个简单的例子来说明节点阻塞是如何干扰原网络的扩散过程的。
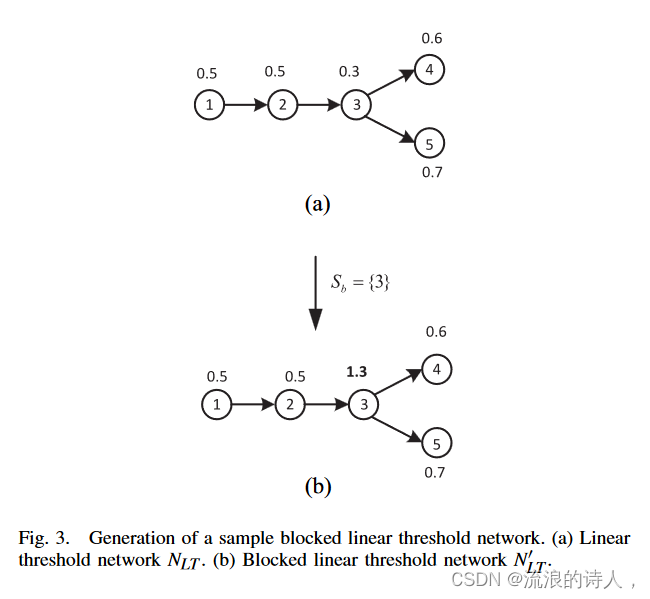
图 3. 样本阻塞线性阈值网络的生成。 (a) 线性阈值网络 NLT 。 (b) 分块线性阈值网络 N' LT 。
示例 2:假设 φ0 ={1} 且 Sb ={3},考虑图 3(a) 中的线性阈值网络。相应的分块线性阈值网络如图3(b)所示。如果没有阻塞,我们有 ∗(NLT ,φ0) = {1, 2, 3, 4, 5}。然而,最终采用者的集合与阻碍设Sb为*(NLT,φ0,Sb)=*(N′LT,φ0)={1, 2}。我们还在表II中展示了带阻塞节点的LTM和阻塞LTM的详细演化,它们是相同的。由于表 II 空间有限,我们表示 t(NLT ) = ⋃t k=0 φt(NLT ,φ0, Sb) 和 t(N′ LT ) = ⋃t k=0 φt(N′ LT ,φ0)。
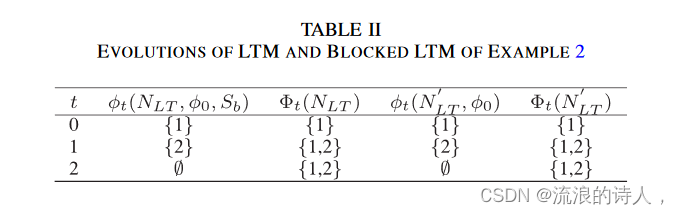
表II 实施例2的LT M和封闭LT M的演变
我们在下面讨论阻塞器的一个属性,这意味着任何阻塞器在阻塞的线性阈值网络中本身都是内聚的,因此永远不能被其他阻塞器激活。
命题 3:给定一个线性阈值网络 NLT = (V, E,θ,w) 和种子集 φ0 ⊆ V,阻塞集合中的任何节点 Sb ⊆ V \ φ0 在相应的阻塞 LTM 中是内聚的 N′ LT = ( V、E、θ′、w)。
证明:对于任何节点 i ∈ Sb,我们有 θ ′ i > 1。因此,它始终保持 Σ j∈X∩Ni wj,i > 1 − θ ′ i,其中 X 表示 V 中包含的任何子集,这意味着 i 是内聚的在网络 N' LT 中。
命题 3 意味着 Sb ⊆ M′,其中 M′ 是分块 LTM 的 V \ φ0 中包含的最大内聚集。
III. PROBLEM STATEMENT AND PROPERTIES
屏蔽一些关键用户是遏制社交网络谣言传播的有效方法。然而,由于成本高昂,控制网络中的所有用户可能是不可能的。因此,我们用有限的预算解决了谣言遏制问题,即我们所说的 top-k 拦截器问题。
A. Problem Statement
问题 1(Top-k Blockers 问题):给定一个 LTM 网络 NLT = (V, E,θ,w) 和种子集 φ0 ⊆ V,令 k 为正整数。找到由 Sb ⊆ V \ φ0 表示的最多 k 个节点的集合,以最小化具有阻止者集合 Sb 的最终采用者集合的基数,即
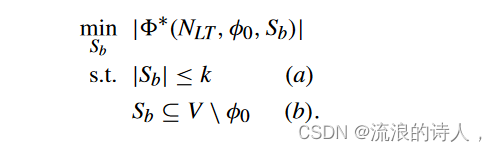
B. Properties
集合函数 f :2V → R 被称为单调递增(或单调递减),如果对于任何两个子集 V1 ⊆ V2 ⊆ V,它满足 f (V1) ≤ f (V2) (或 f (V1) ) ≥ f (V2))。如果对于任何子集 V1 ⊆ V2 ⊆ V 且对于所有 v ∈ V \ V2,它满足 f (V1 ∪{v}) − f (V1) ≥ f,则集合函数 f 被称为子模(或超模) (V2 ∪{v}) − f (V2) (分别为,f (V1 ∪{v}) − f (V1) ≤ f (V2 ∪{v}) − f (V2))。从定义中可以明显看出,如果 f 是单调递减的超模集合函数,则 -f 是单调递增的次模集合函数。因此,最大化单调递增和子模函数等价于最小化单调递减和超模函数。此外,通过最大化单调递增和子模函数的贪心方法获得的解决方案可以近似最优解,并可证明保证率达到 63% [1]。
在下文中,我们证明单调性对于 top-k 阻塞问题的目标函数成立,然而,子模性和超模性则不然。这意味着贪心方法得到的解没有可证明的保证
命题 4:GivenanLTMnetworkNLT = (V, E,θ,w) 和种子集 φ0,top-k 阻塞问题的目标函数,即 | ∗(NLT ,φ0, Sb)|,单调递减,但对于 Sb 而言非超模和非子模。
证明:我们首先证明单调性,即对于任意两个子集 S′ b ⊆ S′′ b ⊆ V \ φ0,它成立 | ∗(NLT , φ0 , S′′ b )|≤ | ∗(NLT ,φ0, S′ b)|.令N′ LT = (V, E,θ′, w) 和 N′′ LT = (V, E,θ′′, w) 表示生成的分块线性阈值网络分别基于阻塞集 S′ b 和 S′′ b,使得 (1) 对于任何节点 i ∈ V \ S′′ b,θ′ i = θ ′′ i = θi; (2) 对于节点 i ∈ S′ b,θ′ i = θ ′′ i = θi + 1; (3) 对于节点 i ∈ S′′ b \ S′ b,θ ′′ i = θi + 1。我们可以得出结论,对于任何 i ∈ V,θ ′′ i ≥ θ′ i。根据命题 2,有相当于证明 | ∗(N′′ LT ,φ0)|≤| ∗(N′ LT ,φ0)|。
假设 M′ 和 M′′ 分别是网络 N′ LT 和 N′′ LT 的 V \ φ0 中包含的最大内聚集。因此,对于任意节点 i ∈ M′,有 Σ j∈M′∩Ni wj,i ≥ 1 − θ′ i ≥ 1 − θ ′′ i 。这意味着 M′ 是 N′′ LT 中的内聚集,然后我们有 M′ ⊆ M′′。感谢引理 1 对最终采用者集的表征,它认为 ∗(N′′ LT ,φ0) ⊆ ∗(N′ LT ,φ0) ,因此 | ∗(N′′ LT ,φ0)|≤ | ∗(N′ LT ,φ0)|。
然后,我们通过两个反例来展示非子模性和非超模性。
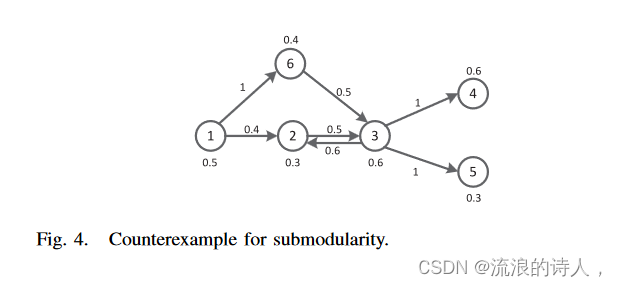
图 4. 子模块性的反例。
非子模:考虑图 4 中的网络。假设谣言的种子集为 φ0 ={1}、S′ b =∅⊆ S′′ b ={4}、v ={2}。那么我们有 | ∗(NLT ,φ0, S′ b∪ {v})|−| ∗(NLT ,φ0,S′ b)|=−4 < | ∗(NLT ,φ0, S′′ b ∪{v})|− | ∗(NLT , φ0 , S′′ b )|=−3。
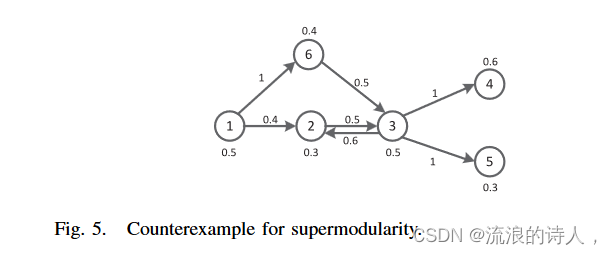
图 5. 超模块化的反例。
非超模:考虑图 5 中的网络。假设谣言的种子集为 φ0 ={1},S′ b =∅⊆ S′′ b ={6},v ={2}。那么我们有 | ∗(NLT ,φ0, S′ b∪ {v})|−| ∗(NLT ,φ0,S′ b)|=−1 > | ∗(NLT ,φ0, S′′ b ∪{v})|− | ∗(NLT , φ0 , S′′ b )|=−4。
IV. OPTIMAL SOLUTIONS
基于 N' LT 的内聚性,可以通过解决线性阈值网络中的数学规划问题来识别前 k 个阻塞者。
A. Nonlinear Formulation
令b ∈{0, 1}n 为Sb 的特征向量,其中bi = 1 表示节点i ∈ V 被阻塞,0 不被阻塞,即

给定anLTMNLT和特征向量b的阻塞集合Sb ⊆ V \ φ0,N′ LT中每个节点i ∈ V的阈值可以写为
![]()
由于网络 NLT 和 N' LT 具有相同的网络结构(V 和 E)和影响权重 w,因此我们可以使用相同的符号 W 来表示 N' LT 的加权邻接矩阵。那么对于 N′ LT 中的内聚集,我们有以下充分必要条件‘
推论 2:给定一个线性阈值网络 NLT = (V, E,θ,w),种子集 φ0 ⊆ V,以及特征向量 b 的阻塞集 Sb ⊆ V \ φ0,asetX 在网络 N′ 中是内聚的 LT = (V,E,θ′,w)当且仅当其特征向量x满足
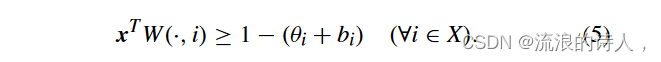
证明:根据引理 2,网络 N′ LT = (V, E,θ′, w) 中的集合 X 是内聚的当且仅当 xT W(·, i) ≥ 1 − θ ′ i 其中 θ ′ i= θi +双。
设 ′ = Diag([θ ′ 1,θ′ 2,...,θ′ n]) 表示网络 N′ LT 中的阈值矩阵,可写为
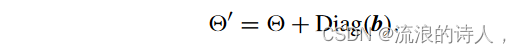
基于Corollary2,我们可以推导出以下命题,将top-k blockers问题转化为NLP问题。
命题 5:给定一个具有 n 个节点的 LTM 网络 NLT = (V, E,θ,w),令 y 为种子集 φ0 ⊆ V 的特征向量,k ∈ R+ 为常数。考虑以下具有二元变量向量 x 和 b 的 NLP:
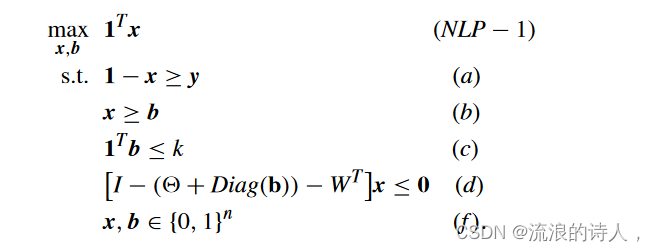
设 x*, b* ∈{0, 1}n 为 (NLP1) 的全局最优解。那么,节点集合 S* b ={i ∈ V|bi* = 1} 就是top-k 拦截器问题的最优拦截器集。具有阻止者集合 S* b 的最终采用者集合为 *(NLT , φ0, S* b) = *(N′ LT , φ0) ={i ∈ V|x* i = 0}。
证明:约束 (b) 确保每个阻塞节点也必须具有内聚性(参见命题 3)。约束(a)和(b)意味着b ≤ x ≤ 1 − y,表明阻塞集合Sb和种子集合φ0是不相交的:这与问题定义中的约束(b)一致。约束 (c) 确保具有特征向量 b 的集合 Sb 是 top-k 阻塞问题的可行解:这与问题定义中的约束 (a) 一致。约束 (a) 确保具有特征向量 x 的集合 M 是 N′ LT = (V, E,θ′, w) 中的内聚集合。然后,约束(d)和目标函数确保M是V\φ0中包含的最大的。因此,由于引理 1,*(N′ LT ,φ0) 具有特征向量 1−x。最后,最大化 M 的目标函数(相当于最小化最终激活的节点数量)确保集合 S*具有特征向量 b* 的 b 是 top-k 阻塞问题的最优解。
B. Linearized Formulation
我们注意到,编程问题(NLP-1)仅包含一个非线性向量约束,即约束(d)。现在我们按条目考虑约束 (d),即,对于所有 i = 1, 2,...,n,它认为’
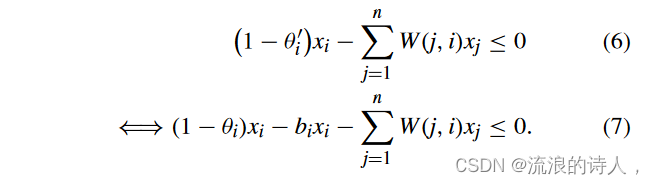
正如我们在约束(7)中看到的,非线性项是两个二元变量的乘积,即 bixi。然后,我们展示如何通过引入一些额外的二元变量来线性化约束(7)。我们定义新的二元变量
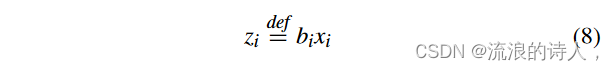
对于所有 i ∈ V。我们总共需要引入的新二元变量的数量为 n。由于 bi 和 xi 是二元变量,因此 (8) 可以通过以下一组线性约束进行线性化:
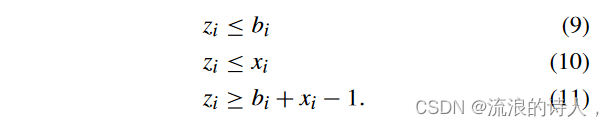
那么,非线性约束(7)可以用以下线性约束代替:
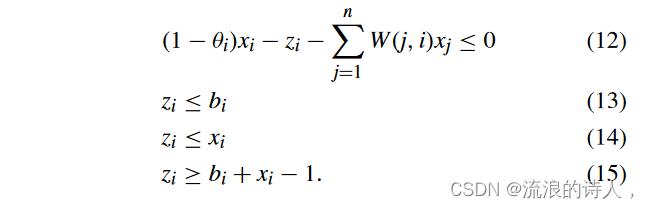
设向量 z ={zi}n。基于上述(NLP-1)的线性化和命题5,我们可以通过求解ILP问题找到最优解。
命题 6:给定一个具有 n 个节点的 LTM 网络 NLT = (V, E,θ,w),令 y 为种子集 φ0 ⊆ V 的特征向量,k ∈ R+ 为常数。考虑以下具有二元变量向量 x、b 和 z 的 ILP:

设 x*, b*, z* ∈{0, 1}n 为 (ILP2) 的最优解。那么节点集合 S* b ={i ∈ V|bi* = 1} 就是 top-k 阻塞问题的最优阻塞集合。具有阻止者集合 S* b 的最终采用者集合为 *(NLT ,φ0, S* b) = {i ∈ V|x* i = 0}。
证明:结果来自命题 5 和之前提出的非线性规划 (NLP-1) 的线性化。非线性公式 (NLP-1) 有 2n 个决策变量和 3n + 1 个约束。通过线性化,(ILP-2)的决策变量和约束的数量分别为3n和6n+1,仍然与n呈线性关系。
C. Reducing the Complexity of the Problem
我们知道,具有大量决策变量和约束的 ILP 问题在计算上很难解决。因此,求解整数线性规划 (ILP-2) 来查找 top-k 阻塞程序无法很好地扩展到大型网络。在这一部分中,我们证明通过遍历整个网络识别出的最优 k 个阻塞器与通过遍历网络的一部分来识别出的最优 k 个阻塞器是等价的。然后 (ILP-2) 的决策变量和约束的数量急剧减少,因此更容易求解。这个想法也可以应用于其他搜索方法,例如第五节中使用的贪婪和中心性方法。
我们通过求解(ILP-2)来搜索整个网络中的最佳阻塞器集合。然而,线性阈值网络是确定性的,并且可以轻松计算由种子激活的最终采用者集合(无阻塞)。我们知道,只有活跃的节点才可能有助于谣言传播。因此,我们只需要在不进行阻塞的情况下,在那些将被激活的节点中寻找阻塞者即可。
最终采用者集合 ∗(NLT ,φ0) 可以通过算法 A1 或求解 (ILP-1) 来确定。然后,我们可以通过定义 ˆ V = ∗(NLT ,φ0) 从原始网络 NLT = (V, E,θ,w) 中提取活动子网络 ˆ NLT = ( ˆ V, ˆ E, ˆ θ, ˆ w) ⊆V, ˆ E = (ˆ V× ˆ V) ∩ E,对于所有 u ∈ ˆ V 来说,ˆ θu = θu,对于任何 (u, v) ε ˆ E 来说 ˆ wu,v = wu,v。
由于网络 NLT 和 ^ NLT 的种子集相同,因此我们在以下符号中省略 φ0。令 φt(NLT ) (分别为 φt( ˆ NLT ))和 ∗(NLT ) (分别为 *( ˆ NLT )) 表示网络 NLT 中在步骤 t 激活的节点集(分别为 ˆ NLT ),并且网络 NLT 中的最终采用者集(分别为 ^ NLT ),Nv(NLT ) (分别为 Nv( ˆ NLT ))表示网络 NLT 中的邻居集(分别为 ^ NLT )。那么我们有 Nv( ^ NLT ) ⊆ Nv(NLT )。此外,我们在下面证明网络 NLT 的演化过程可以用活动子网 ^ NLT 的演化过程来表示。
定理 1:给定一个 LTM 网络 NLT = (V, E,θ,w) 和种子集 φ0 ⊆ V,网络 NLT 的演化过程等价于其对应的活动子网络 ˆ NLT = ( ˆ V, ˆ E , ˆ θ, ˆ w),即对于所有 t ≥ 0, φt(NLT ) = φt( ˆ NLT )。 证明:该陈述显然适用于 t = 0,因为种子集相同。然后我们通过归纳证明 t ≥ 1 的结果。
我们从 t = 1 开始。对于任何节点 v,v ∈ φ1(NLT ) 当且仅当它满足 Σ u∈φ0∩Nv(NLT ) wu,v ≥ θv。我们也有 φ0 ∩ Nv(NLT ) = (φ0 ∩ ∗(NLT ) ) ∩ Nv(NLT ) = φ0 ∩ ( *(NLT ) ∩ Nv(NLT )) 且 φ0 ∩ Nv( ˆ NLT ) = φ0∩(Nv(NLT )∩ *(NLT )) 因为 a 的近邻集活动子网 ^ NLT 中的节点 v 与原始网络 NLT 稳态下的活动内邻居集相同。因此, φ0 ∩ Nv(NLT ) = φ0 ∩ Nv( ˆ NLT ),并且
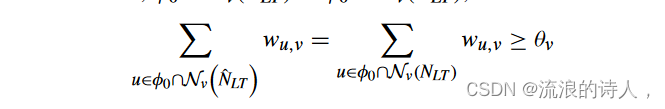
这意味着 v ∈ φ1( ˆ NLT )。那么我们有 φ1(NLT ) = φ1( ˆ NLT )。
在时间步 t = 2,对于任何节点 v,v ∈ φ2(NLT ) 当且仅当它保持 Σ u∈φ0∪φ1(NLT )∩Nv(NLT ) wu,v ≥ θv。由于 φ1(NLT ) = φ1( ˆ NLT ),我们有 Σ u∈φ0∪φ1( ˆ NLT )∩Nv(NLT ) wu,v = Σ u∈φ0∪φ1(NLT )∩Nv(NLT ) wu,v ≥ θv 意味着 v ∈ φ2( ˆ NLT ) 且 φ2(NLT ) = φ2( ˆ NLT )。
那么,在任意时间步长 t ≥ 2,对于任意节点 v
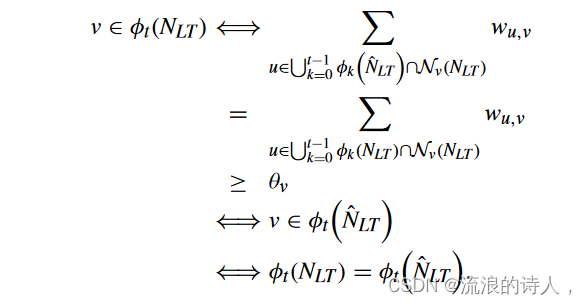
这样就完成了证明。
由于 top-k 阻塞问题涉及阻塞一些在没有阻塞的情况下将被激活的节点,即 Sb ⊆ ∗(NLT ,φ0),并且由于定理 1,我们得到以下结果。
推论 3:给定 LTM 网络 NLT = (V, E,θ,w) 和种子集 φ0 ⊆ V,网络 NLT 中 top-k 阻塞问题的最优解等价于其活动子网络 ˆ NLT 中的最优解= ( ˆ V, ˆ E, ˆ θ, ˆ w)。

设 ^ n =| *(NLT,φ0)|表示在没有阻塞的情况下最终采用者的数量。令 ˆ ∈ [0, 1]ˆ n׈ n 和 ˆ W ∈ [0, 1]ˆ n׈ n 分别表示活动子网络 ˆ NLT 的阈值子矩阵和加权邻接子矩阵。
集合 ˆ X⊆ ˆ V 的特征向量 ˆ x 由通用集合 ˆ V 定义,即 ˆ x ∈{0, 1}ˆ n。例如,假设 ˆ V= {1, 2, 3, 4, 5, 7, 9} 且 ˆ X ={2, 7, 9}。则其特征向量为 ˆ x = [0, 1, 0, 0, 0, 1, 1]T
top-k 阻塞问题可以通过算法 1 来解决。正如我们所见,(ILP-3) 比 (ILP-2) 更容易解决,因为它有 3ˆ n 个决策变量和 6ˆ n + 1 个约束,通常我们有 ^ n n。阿塞莫格鲁等人。 [8]提出了最终采用者数量的上限,即 ˆ n ≤ Σ|φ0| k=1 |Mk|,如果网络 NLT 可以划分为 r ≥|φ0|不相交的内聚集和 {Mk}r k=1 是按降序排列的。他们的基数。
注意,(ILP-3)的约束(d)中的矩阵ˆI不再是单位矩阵,而是一个对角矩阵,其对角元素为ˆW各列之和,即ˆI(i, i) = Σ j∈ ˆ Vˆ W(j, i)。
V. A PPROXIMATE OR HEURISTIC SOLUTIONS
为了更好地评估我们上面提出的 ILP 方法,我们还考虑了一些近似或启发式方法来选择一组 top-k 拦截器。
A. Greedy
我们不必在整个网络中搜索前 k 个拦截器,其大小有时 n 非常大,我们可以只关注由于推论 3,我们可以在活动子网络中找到相同的阻塞者集合。该算法首先计算最终采用者的集合,假设没有阻塞(第 3 行),这可以通过算法 A1 在 O(nd) 时间内完成。然后我们提取活动子网(第 4 行)。在活动子网络中,我们迭代地选择一个阻止程序,如果它被阻止,它可以最大限度地减少谣言传播(第 7 行)。拦截器识别过程停止,直到找到 k 个拦截器。在每次迭代中,需要确定任何要被阻塞的节点 i ∈ ˆ V \ (φ0 ∪ Sb) 的最终采用者集合。这样的计算过程可能需要检查所有节点的状态,因此该过程可以在 O(^ n2 ^ d) 时间内完成,其中 ^ d 表示活动子网络的平均度。因此,附录中算法 A2 所示的贪婪方法的时间复杂度为 O(nd + kˆ n2 ˆ d)。
B. Degree
度中心性是一种简单且广泛使用的衡量网络中节点重要性的方法。一个人的出度就是它的出邻居的数量。所有节点均按其出度排序,除了活动子网络中的谣言种子之外的前 k 个节点被选择为阻塞者,即 Vd ∩ ( ˆ V \ φ0) 中的前 k 个节点,其中 Vd 是有序集V 根据节点度数。计算所有节点度数的复杂度为 O(nd)。
C. Source-Aware Betweenness Centrality (Source-BC)
然后,我们提出一种基于介数中心性的启发式方法,这是一种基于最短路径的中心性度量。已知最快的计算介数中心性的方法 [39] 需要 O(nm) 时间,其中 m 表示边的数量。然而,为了找到 top-k 阻塞者,不需要像 Brandes 算法 [39] 那样枚举任意两个节点之间的所有最短路径。我们只关心哪个节点从谣言种子到所有不活跃节点被传递的次数最多。因此,我们只需要枚举从子集S到子集V\S的最短路径。我们将这种方法称为源感知介数中心性。将任何节点 u ∈ V 的源感知介数中心性表示为 cb(u|S),可以通过以下方式计算
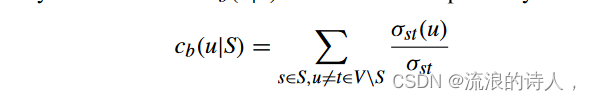
其中S表示源节点的集合。
从上面的分析可以看出,采用Brandes算法计算源感知介数中心性需要O(|S|m)(等于O(|S|nd)),其中|·|是集合的基数。这种方法的前 k 个阻塞者是活动子网络中具有最高源感知介数中心性的前 k 个节点,即 Vsbc ∩ ( ˆ V \ φ0) 中的前 k 个节点,其中 Vsbc 是根据节点的 V 的有序集合' 源感知介数中心性的值。
请注意,由于目标函数的非子模性和非超模性,通过包括贪心法在内的启发式方法获得的解没有近似保证。在这项工作的其余部分中,我们用 ILP 表示使用完整编程问题 (ILP-2) 的方法,并且R-ILP 使用简化编程问题的方法 (ILP-3)。 ILP和R-ILP的二元决策变量数分别为3n和3^n。我们在表 III 中揭示了上述启发式的一般时间复杂度。
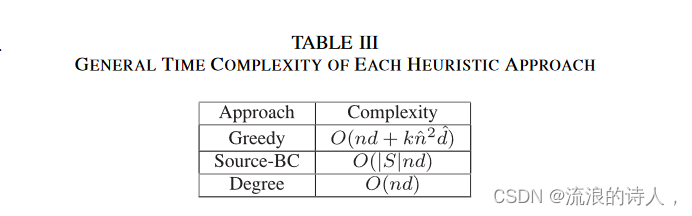
表 III 每种启发式方法的一般时间复杂度
VI. EXPERIMENTAL EVALUATION
A. Experimental Setup
在这一部分中,我们对一个合成网络和三个从小到大扩展的现实世界网络进行了一系列实验,以评估我们的数学规划方法的性能以及解决 LTM 的 top-k 阻塞问题的三种启发式方法。合成数据集具有如下定义的一些特定结构属性。
1)无标度:如果节点的度遵循幂律度分布,则网络称为无标度。现实世界中无标度网络的典型例子是协作网络、金融网络等。这种类型的具有 500 个节点的基准网络是通过采用 Barabási-Albert 模型生成的 [40]
现实世界网络采用SNAP.1
1) LastFM:该网络由来自亚洲国家的音乐网站(称为 LastFM)的用户组成。
2) Deezer:该网络由来自欧洲国家的 Deezer 用户组成。
3)DBLP:这是计算机科学领域的DBLP合着网络。
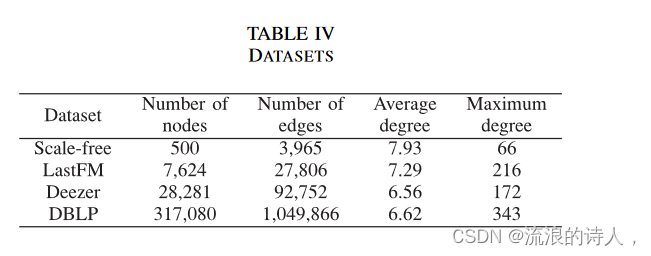
表IV总结了这些网络的统计信息,这些网络都假设为无向的,即由无向弧连接的两个节点彼此是邻居。为了公平地估计和比较所提出的方法的性能,对于给定的谣言种子集 φ0 和 k,我们在 10 个随机生成的线性阈值网络 NLT = (V, E,θ,w) 上运行它们。在每次运行中,都会确定一组大小为 k 的前 k 个阻止者 Sb,最后我们取 | 的平均值。 *(NLT,φ0,Sb)|每个数据集的 10 个随机 LTM 网络。为给定数据集生成的所有 LTM 网络都具有相同的网络结构,即 V、E 和影响权重 w,但在 (0, 1] 中均匀随机选择的不同阈值 θu。此外,我们假设 |φ0对于所有网络,|=10 且 k 的范围为 1 到 20。由他们的学位决定。也就是说,谣言从每次运行中度数最高的 10 个节点传播。请注意,我们可以将谣言种子集大小更改为不同的值,而不影响谣言遏制的相对性能和所有方法的计算时间。
所有实验均在 3.00 GHz Intel Core i7-9700U CPU 和 16 GB 内存上使用 MATLAB 进行编码。所有整数线性规划均使用工具箱 SCIP 求解,其学术许可证可在 https://www.inverseproblem.co.nz/OPTI/index.php/Solvers/SCIP 获取。
B. Experimental Results and Discussions
这五种不同的方法根据谣言抑制及其计算时间进行了评估。谣言在四个权重不均匀的网络上传播的不同数量的阻止者(随机生成,但确保对于所有 v ∈ V,我们有 Σ u ∈ Nv wuv = 1)如图 6 所示。计算时间和标准差表 V 中显示了通过每种方法选择 20 个阻断剂的情况。我们进行了以下观察。
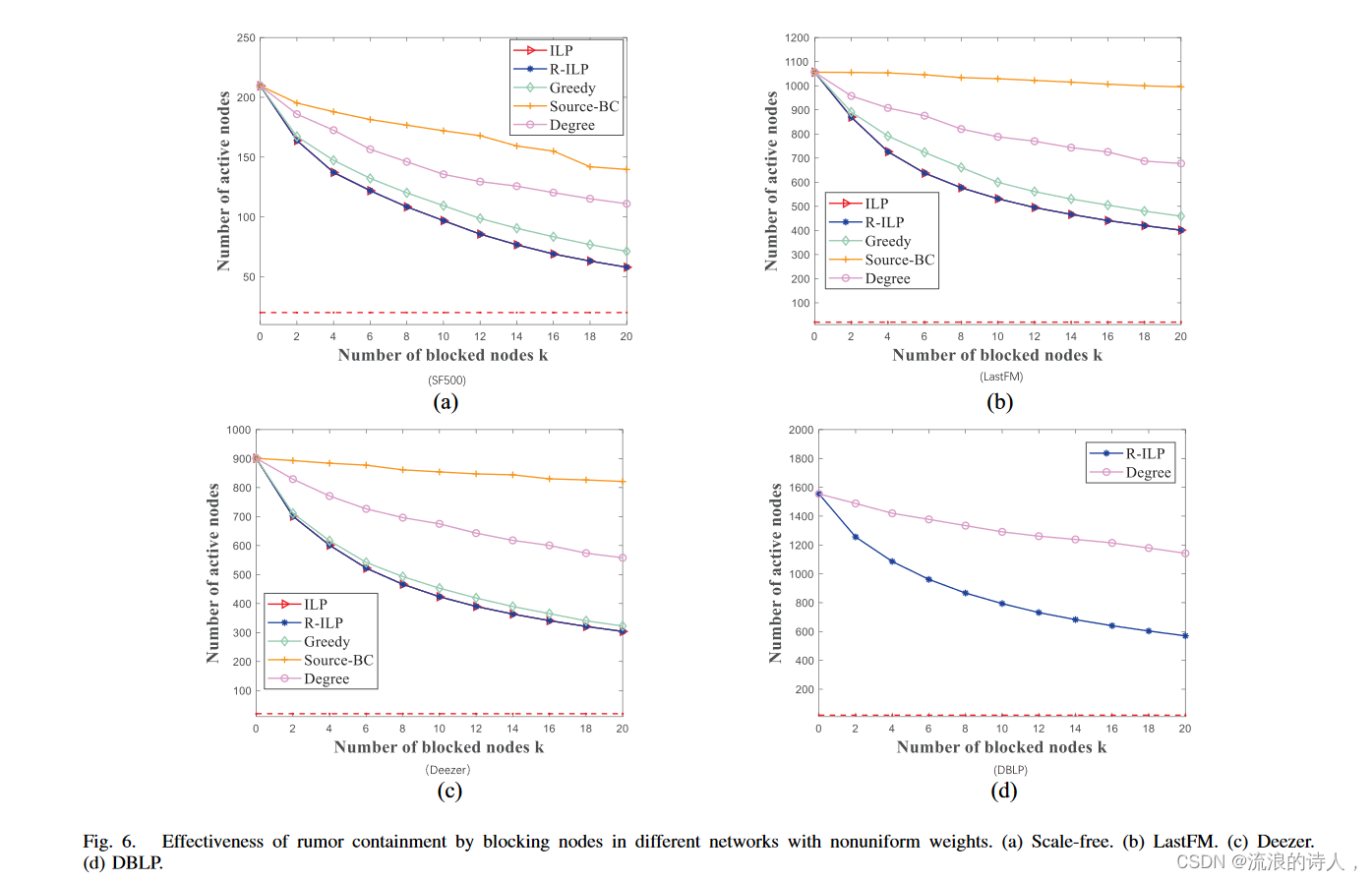
图 6. 通过阻止权重不均匀的不同网络中的节点来遏制谣言的有效性。 (a) 无标度。 (b) 最后调频。 (c) 迪泽。 (d) DBLP。
1) 在小型网络中,即 Scale-free 和 LastFM,R-ILP 的运行速度比 ILP 快三到八倍。然而,它们的差距随着网络规模的增大而增大,例如,在中型 Deezer 网络中,R-ILP 的运行速度比 ILP 快 55 倍。 R-ILP可以在Scale-free、LastFM和Deezer网络中不到一秒的时间内找到最佳的拦截器集合,可以将谣言传播减少约70%。在包含 30 万个节点的 DBLP 网络中,ILP 和 Greedy 无法在合理的时间内给出结果,因此,我们只比较 R-ILP 和 Degree,它们比 Source-BC 表现更好、更快。 R-ILP 在几秒钟内找到解决方案,将谣言传播减少 68%。
2)在所有网络中,Greedy计算近似ILP和R-ILP获得的最优解的解。然而,如前所述,目标函数 ∗(φ0, Sb) 是单调递减的,但非超模 w.r.t. Sb ⊆ V \ φ0。因此,贪心法得到的解对于最优解没有可证明的近似保证[1]。考虑到其计算时间,Greedy 的运行速度比 R-ILP 慢得多。并且它们的计算差距将随着底层网络或其子活动网络中的节点数量而增加。此外,从表V中我们可以看出,Greedy在计算时间方面有很大的标准差。也就是说,Greedy 的计算时间很大程度上取决于子主动网络的大小。在随机选择阈值的网络的每次运行中,最终采用者的数量可能会显着不同,因此相应的计算时间会发生变化。
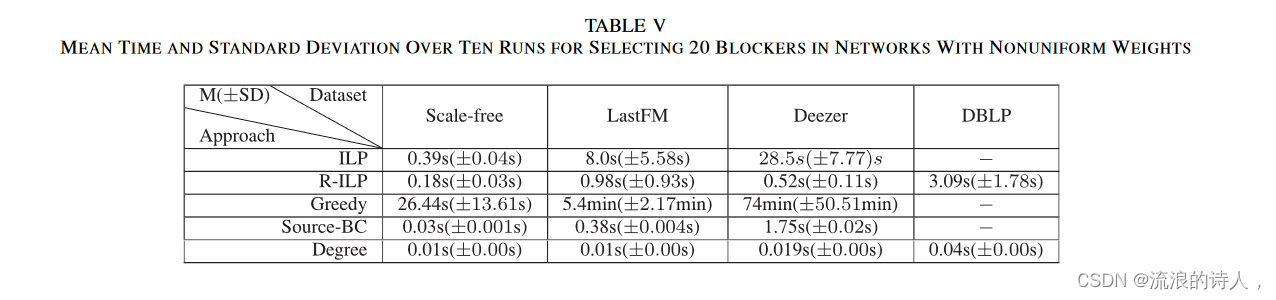 在权重不均匀的网络中选择 20 个阻断剂的 10 次运行的平均时间和标准差
在权重不均匀的网络中选择 20 个阻断剂的 10 次运行的平均时间和标准差
3)基于中心性的方法,即Degree和Source-BC,在谣言遏制方面表现不佳尽管它们在小型无标度网络中运行速度比 R-ILP 快得多。然而,它们的计算时间随着网络规模的增大而增加,甚至在网络 Deezer 中超过了 R-ILP。 Degree 在所有网络中均优于 SourceBC。在 Scale-free、LastFM 和 Deezer 网络中,阻塞按 Degree(分别为 Source-BC)选择的 20 个节点可以减少 47%(分别为 33%)、36%(分别为 6%)的谣言传播、 和 38%(分别为 9%)。
4) 均匀或不均匀影响权重的存在对每种方法的结果没有影响。
VII. CONCLUSION AND FUTURE WORK
为了识别谣言遏制的前 k 个阻止者,我们首先在线性阈值网络中提出该问题的非线性公式,然后引入一些新的决策变量来线性化非线性公式。我们可以通过证明给定种子集,整个网络中的演化过程与其活动子网络中的演化过程等效来进一步降低ILP的复杂性。为了更好地评估我们改进的 ILP 方法的有效性,我们在一个合成网络和三个现实世界网络中将其与基于贪婪的方法和两种基于中心性的方法进行了比较。我们可以从实验结果中了解到:我们的 ILP 方法优于贪婪方法和中心性方法,并且由于其合理的执行时间而适用于大规模网络。
我们知道,基于 ILP 的解决方案无法很好地适应大型网络。因此,我们未来的工作将包括探索降低复杂性的方法,通过将 ILP 与分而治之的方案相结合来找到接近最优的解决方案。谣言遏制的另一个未来方向可能会考虑多重性,其动机是真实网络中的代理之间可以存在不止一种连接模式。社交网络通常是耦合的,因为它们有一些重叠的用户。多重性促进了真实社会场景中的信息传播,这使得多重网络中的谣言控制变得更加困难[41]。