为后续更好从频域层面分析控制系统的稳定性，本节首先介绍在后续分析中用到的辐角原理。
根据复变函数对数的定义，有 $$lnf(s)=ln|f(z)|+i(argf(z)+2k\pi ),k=0,\pm 1,\pm 2,\dots$$

辐角原理（即Cauchy原理）

定义 $$\frac{1}{2\pi i}{\int }_C\frac{f^{{}^{\prime }}(z)}{f(z)}dz=\frac{1}{2\pi i}{\int }_{C}d(ln(f(z)))\text{\hspace{1em}(1)}$$ 为复变函数 $f(z)$ 的对数函数。
根据复变函数对数的定义可知$$lnf(z)=ln|f(z)|+i(argf(z)+2k\pi ),k=0,\pm 1,\pm 2,\dots \text{\hspace{1em}(2)}$$

引理 设 $C$ 为一条闭曲线，若 $f(z)$ 符合条件：
(1) $f(z)$ 在 $C$ 内部除可能的极点外解析，即 $f(z)$ 为亚纯函数；
(2) $f(z)$ 在 $C$ 上解析且不为零，则有
$$\frac{1}{2\pi i}{\int }_C\frac{f^{{}^{\prime }}(z)}{f(z)}dz=N(f,C)-P(f,C),\text{\hspace{1em}(3)}$$
其中 $N(f,C)$，$P(f,C)$ 分别表示 $f(z)$ 在 $C$ 的内部的零点和极点的个数（个数的计算包含零点或极点的重数）

引理分析

设 $s$ 为复变量，$F(s)$ 是有理式函数，设$$F(s)=\frac{k(s-z_1)(s-z_2)\dots (s-z_m)}{(s-p_1)(s-p_2)\dots (s-p_n)},$$其中 $z_i$，$p_j$ （$i=1,2,\dots ,m;j=1,2,\dots ,n$）分别代表$F(s)$ 的零点和极点。
假设复变量 $s$ 变化，在 $s$ 平面（自变量的复平面）中形成一条不通过 $F(s)$ 零极点的闭合路径 $\Gamma$，其通过$F(s)$ 映射后得到对应的闭合曲线 ${\Gamma }_F$（即闭合路径 $\Gamma$ 的像或映射）(如图一所示)
注意 此处需要注意的是在实数域上的映射关系是基于点的映射，因变量与自变量的关系可以直接通过横纵坐标轴表示。但在复数域上，任何一个变量均具有实部与虚部，变量的表示本身需要一个平面的坐标轴，其映射关系需要用到立体维度的空间来表示。
如图一为了更简便清晰表示复数域上的映射关系，使用自变量与因变量的坐标截面来表示定义在复数域上的映射关系。

图一说明： 图中坐标轴上的×与●分别表示 $F(s)$ 的极点与零点。路径 $\Gamma$ 包围一个零点。
图一中的移动中，被路径 $\Gamma$ 包围的零点的坐标变换如下图所示：

                   ~~~~~~~~~~~~~~~~~~                   
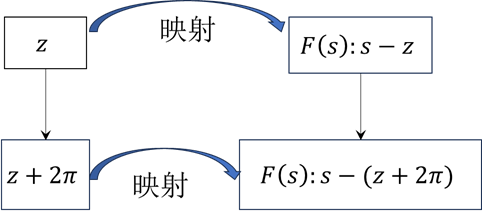
观察上图，当复变量 $s$沿路径 $\Gamma$ 顺时针移动一周时，被包围的零点矢量 ($s-z_i$) 相角的变化为 $-2\pi$。极点矢量 ($s-p_j$) 位于分子位置，若其被路径 $\Gamma$顺时针移动时被包围，其相角的变化为 $2\pi$。未被包围的零极点矢量其相角变化为0。且移动过程中复变函数的模不发生变化。以上图为例，路径 $\Gamma$包围一个零点，复变函数 $F(s)$ 的相角变化为$$\Delta \angle F(s)=\Delta [\sum _{i=1}^m\angle (s-z_i)-\sum _{j=1}^n\angle (s-p_j)]=\Delta \angle (s-z_1)=-2\pi .$$即矢量 $F(s)$ 沿曲线 ${\Gamma }_F$ 绕原点顺时针转动了一圈。同理，若包围在路径 $\Gamma$ 中的是$F(s)$ 的一个极点，那么当 $s$ 沿路径 $\Gamma$ 顺时针转动一圈时，矢量 $F(s)$ 将沿曲线 ${\Gamma }_F$绕坐标原点逆时针转动一圈。
则经以上分析，辐角原理可总结如下：

辐角原理定义与证明

辐角原理 设 $D$ 为闭曲线 $C$ 所围成的区域，若（1）$f(z)$ 在区域 $D$ 内除可能的极点外解析，即为亚纯函数；（2）$f(z)$ 在 $C$ 上解析且不为0，则$$\frac{1}{2\pi }{\Delta }_{C}argf(z)=\frac{1}{2\pi i}{\int }_C\frac{f^{{}^{\prime }}(z)}{f(z)}dz=N(f,C)-P(f,C).$$即沿着闭曲线 $C$ 正向绕行一周后辐角 $argf(z)$ 的改变量${\Delta }_{C}argf(z)$除以$2\pi$ 等于$f(z)$ 在 $C$ 的内部的零点和极点的个数的差值。

证明.

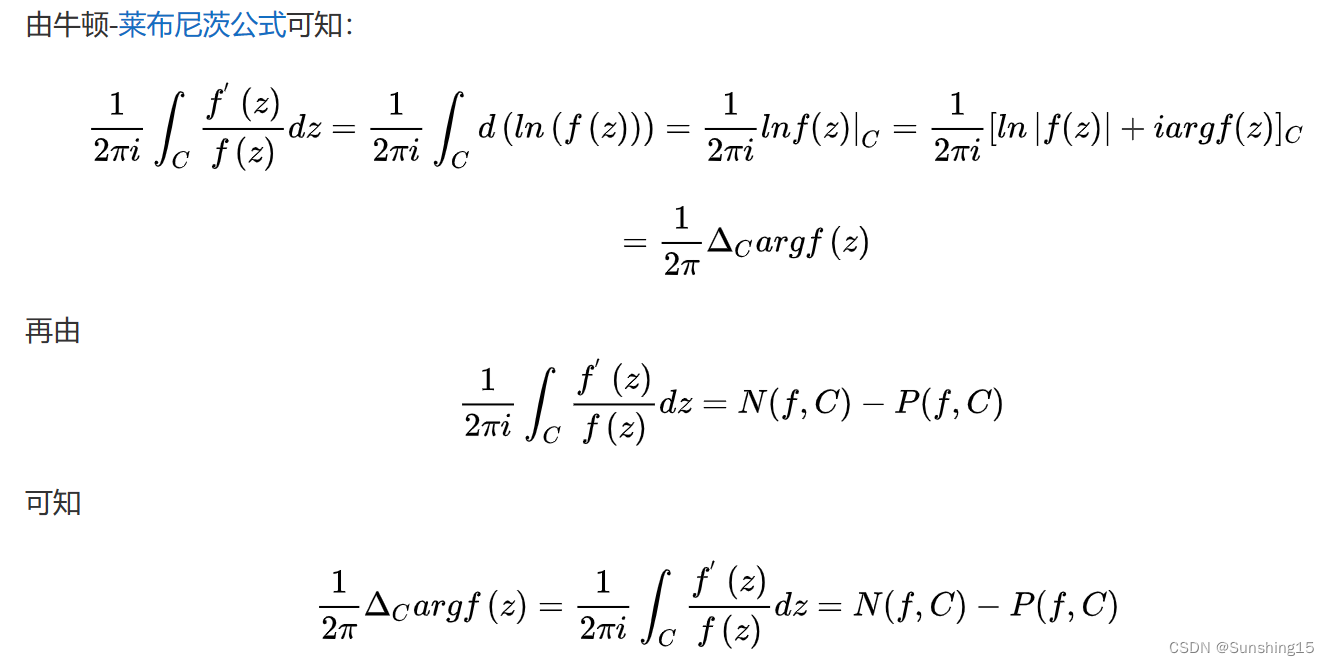
参考文献

[1] 复变函数在自动控制原理中的应用之Cauchy原理
[2] 辐角原理
[3] 杨贺菊，姚卫．复变函数 ．清华大学出版社．2015