洛谷 P4148：简单题 ← KD-Tree模板题

news2025/1/8 20:29:53

【题目来源】
https://www.luogu.com.cn/problem/P4148

【题目描述】
你有一个 N×N 的棋盘，每个格子内有一个整数，初始时的时候全部为 0，现在需要维护两种操作：
● 1 x y A → 1≤x,y≤N，A 是正整数。将格子 (x,y) 里的数字加上 A。
● 2 x1 y1 x2 y2 → 1≤x1≤x2≤N，1≤y1≤y2≤N。输出 x1,y1,x2,y2 这个矩形内的数字和
● 3 → 无终止程序

【输入格式】
输入文件第一行一个正整数 N。
接下来每行一个操作。每条命令除第一个数字之外，均要异或上一次输出的答案 last_ans，初始时 last_ans=0。

【输出格式】
对于每个 2 操作，输出一个对应的答案。

【输入样例】
4
1 2 3 3
2 1 1 3 3
1 1 1 1
2 1 1 0 7
3

【输出样例】
3
5

【说明/提示】
1≤N≤5×10^5，操作数不超过 2×10^5 个，内存限制 20MB，保证答案在 int 范围内并且解码之后数据仍合法。

【算法分析】
● KD-Tree 作为一种二分查找树，由 Jon Louis Bentley 发明。所谓 KD-Tree，即 Multidimensional Binary Search Tree 的简称，其中的 K 表示数据空间的维度。KD-Tree 高效支持高维空间的最近邻搜索、空间搜索，因此深入了解 KD-Tree 的原理以及底层实现，对机器人或无人驾驶领域的从业者来说，意义非凡。

● KD-Tree 的基本操作包括维度划分、建树、插入新结点、删除结点、寻找第 i 维的最小值等。
其中，维度划分常用轮转法及最大方差法。
（1）轮转法，即按维度交替划分。例如，若共有 K 个维度。那么，第 dep 层按 dep%K 划分，第 dep+1 层按 (dep+1)%K 划分，……。轮转法适用于所有维度的数据分布都比较均匀的情形。特别地，针对二维平面，按 x，y 交替划分，奇数层按 x 划分，偶数层按 y 划分。
（2）最大方差法，适用于某些维度的值变化不大的情况。例如，平面上呈现为一条横线的 n 个点，x 值分布均匀，y 值相差很小，若按 y 划分没有太大意义，故选方差最大的维度 x 进行划分。方差的计算公式为： $s^2=\frac{1}{n}\sum_{i=1}^{n}(x_i-\mu)^2$ ，其中 μ 为 x 的均值。
无论采用哪种划分方法对某个维度进行划分，一般选取此维度的中位数作为划分点，并将其作为二叉树某个子树的根。中位数常用 STL 中的 nth_element() 函数直接得到。

● 在数学中，给定 n 个数，当 n 为偶数时，中位数为位序 n/2+1 对应的数；当 n 为奇数时，中位数为位序 (n+1)/2 对应的数。例如：
求 (23、29、20、32、23、21、33、25) 及 (30、20、 20、 20、 10) 的中位数。
解：对 (23、29、20、32、23、21、33、25) 排序后，得 (20、21、23、23、25、29、32、33)。
由于此题中 n=8，故中位数为位序 n/2+1=8/2+1=5 对应的数25。
对 (30、20、 20、 20、 10) 排序后，得 (10、20、 20、 20、 30) 。
由于此题中 n=5，故中位数为位序 (n+1)/2=(5+1)/2=3 对应的数20。

● 利用轮转法构建 KD-Tree 的示例如下：
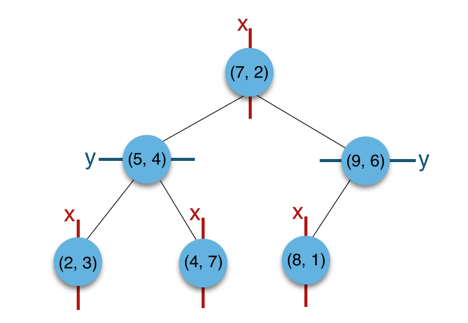
给定二维平面点 (x,y) 的集合 (2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)，利用轮转法构建 KD-Tree 的过程示例如下。
（1）构建根结点：由于奇数层按 x 划分，故将点集 (2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2) 按 x 值排序，得 (2,3)，(4,7)，(5,4)，(7,2)，(8,1)，(9,6)，其中位数位序对应的结点值为 (7,2)。即将结点 (7,2) 作为根结点，(2,3)，(4,7)，(5,4) 将位于 (7,2) 的左子树，(8,1)，(9,6) 将位于 (7,2) 的右子树。
（2）构建左子树：由于偶数层按 y 划分，故将点集 (2,3)，(4,7)，(5,4) 按 y 值排序，得 (2,3)，(5,4)，(4,7)，其中位数位序对应的结点值为 (5,4)。即将结点 (5,4) 作为根结点，(2,3) 将位于 (5,4) 的左子树，(4,7) 将位于 (5,4) 的右子树。
（3）构建右子树：由于偶数层按 y 划分，故将点集 (8,1)，(9,6) 按 y 值排序，得 (8,1)，(9,6)，其中位数位序对应的结点值为 (9,6)。即将结点 (9,6) 作为根结点，(8,1) 将位于 (9,6) 的左子树，(9,6) 右子树为空。
（4）其他结点按上述步骤逐个添加到 KD-Tree 中。

最终构建所得的 KD-Tree 如下图所示。

可以看出，对二维平面构建 KD-Tree 的过程，就是将二维平面逐步划分的过程。如下图所示。

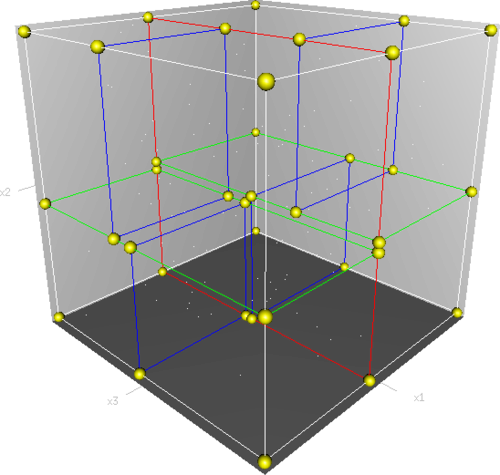
维基百科给出了对三维空间构建 KD-Tree 的过程及空间划分。首先，边框为红色的竖直平面将整个空间划分为两部分。其次，此两部分又分别被边框为绿色的水平平面划分为上下两部分。最后，此 4 个子空间又分别被边框为蓝色的竖直平面分割为两部分，变为 8 个子空间，此 8 个子空间即为叶子结点。如下图所示。

● KD-Tree 的建树、插入新结点、删除结点等操作，会打破 KD-Tree 的平衡。替罪羊树常用于维护 KD-Tree 的平衡。KD-Tree 当 K 等于 1 时，就是一颗替罪羊树。
● 快读：https://blog.csdn.net/hnjzsyjyj/article/details/120131534

【算法代码】

#include <bits/stdc++.h>
using namespace std;

const int maxn=1e5+5;
const double alpha=0.75;
const int K=2;

int n;
int num;
int last,root,len;
int p[K],q[K][2];
int A,D;
int h[maxn];

struct KD_Tree {
    int le,ri;
    int sum,val,size;
    int minv[K],maxv[K],d[K];
} tr[maxn];

bool cmp(const int &a,const int &b) {
    return tr[a].d[D]<tr[b].d[D];
}

int read() { //fast read
    int x=0,f=1;
    char c=getchar();
    while(c<'0' || c>'9') { //!isdigit(c)
        if(c=='-') f=-1;
        c=getchar();
    }
    while(c>='0' && c<='9') { //isdigit(c)
        x=x*10+c-'0';
        c=getchar();
    }
    return x*f;
}

void update(int x) {
    int le=tr[x].le, ri=tr[x].ri;
    tr[x].size=tr[le].size+tr[ri].size+1;
    tr[x].sum=tr[le].sum+tr[ri].sum+tr[x].val;
    for(int i=0; i<K; i++) {
        if(le) {
            tr[x].maxv[i]=max(tr[le].maxv[i],tr[x].maxv[i]);
            tr[x].minv[i]=min(tr[le].minv[i],tr[x].minv[i]);
        }
        if(ri) {
            tr[x].maxv[i]=max(tr[ri].maxv[i],tr[x].maxv[i]);
            tr[x].minv[i]=min(tr[ri].minv[i],tr[x].minv[i]);
        }
    }
}

void build(int &x,int le,int ri,int pos) {
    if(le>ri) return;
    int mid=(le+ri)>>1;
    D=pos;
    nth_element(h+le,h+mid+1,h+ri+1,cmp);
    x=h[mid];
    tr[x].sum=tr[x].val;
    for(int i=0; i<K; i++) tr[x].maxv[i]=tr[x].minv[i]=tr[x].d[i];
    build(tr[x].le,le,mid-1,(pos+1)%K);
    build(tr[x].ri,mid+1,ri,(pos+1)%K);
    update(x);
}

void erase(int &x) {
    if(!x) return;
    h[++num]=x;
    erase(tr[x].le), erase(tr[x].ri);
    x=0;
}

void rebuild(int &x,int pos) {
    h[num=1]=++len;
    tr[len].size=1;
    for(int i=0; i<K; i++) tr[len].d[i]=p[i];
    tr[len].val=tr[len].sum=A;
    erase(x);
    build(x,1,num,pos);
}

void insert(int &x,int pos) {
    if(!x) {
        tr[x=++len].size=1, tr[x].val=tr[x].sum=A;
        for(int i=0; i<K; i++) tr[x].maxv[i]=tr[x].minv[i]=tr[x].d[i]=p[i];
        return;
    }
    if(p[pos]<tr[x].d[pos]) {
        if(tr[tr[x].le].size>tr[x].size*alpha) rebuild(x,pos);
        else insert(tr[x].le,(pos+1)%K);
    } else {
        if(tr[tr[x].ri].size>tr[x].size*alpha) rebuild(x,pos);
        else insert(tr[x].ri,(pos+1)%K);
    }
    update (x);
}

bool check_range(int x) {
    if(!x) return 0;
    for(int i=0; i<K; i++) {
        if(q[i][0]>tr[x].minv[i] || q[i][1]<tr[x].maxv[i]) return 0;
    }
    return 1;
}

bool check_point(int x) {
    if(!x) return 0;
    for(int i=0; i<K; i++) {
        if(tr[x].d[i]<q[i][0] || tr[x].d[i]>q[i][1]) return 0;
    }
    return 1;
}

bool check(int x) {
    if(!x) return 0;
    for(int i=0; i<K; i++) {
        if(q[i][1]<tr[x].minv[i] || q[i][0]>tr[x].maxv[i]) return 0;
    }
    return 1;
}

void query(int x) {
    if(check_range(x)) {
        last+=tr[x].sum;
        return;
    }
    if(check_point(x)) last+=tr[x].val;
    if(check(tr[x].le)) query(tr[x].le);
    if(check(tr[x].ri)) query(tr[x].ri);
}

int main() {
    n=read();
    while(1) {
        int op=read();
        if(op==1) {
            for(int i=0; i<K; i++) p[i]=read()^last;
            A=read()^last;
            insert(root,0);
        }

        if(op==2) {
            for(int i=0; i<=1; i++) {
                for(int j=0; j<K; j++) q[j][i]=read()^last;
            }
            last=0;
            query(root);
            printf("%d\n",last);
        }

        if(op==3) break;
    }

    return 0;
}

/*
in:
4
1 2 3 3
2 1 1 3 3
1 1 1 1
2 1 1 0 7
3

out:
3
5
*/

【参考文献】
https://www.cnblogs.com/PaulShi/p/10131078.html
https://www.cnblogs.com/flyinggod/p/8727584.html
https://www.cnblogs.com/Tenshi/p/15846105.html
https://oi-wiki.org/ds/kdt/
https://www.cnblogs.com/AWCXV/p/7632254.html
https://blog.csdn.net/qq_45323960/article/details/109698448
https://www.cnblogs.com/sitiy/p/15380688.html
https://www.luogu.com.cn/problem/solution/P4148
https://www.cnblogs.com/cmy-blog/p/kdtree.html
https://zhuanlan.zhihu.com/p/112246942
https://blog.csdn.net/hnjzsyjyj/article/details/128647972