考题形式:
- 第一题:代码填空 4-5空 8-10
- 第二题:时间复杂度 / 代码策略
- 第三题:拓展,跟一组数据,把数据带入代码中,求解
基础知识及技巧:
1. 分治法:
基础知识:
- 概念:对于一个规模为n的问题,若该问题可以容易地解决则直接解决;否则,将其分解为k个规模较小的子问题,这些子问题相互独立,并且与原问题形式相同,递归地解决这些子问题,然后,将各子问题的解合并得到原问题的解。
- 步骤:分解、解决、合并。
- 特点:

递归技术:
- 概念:在运行的过程中调用自己的过程。
二分查找法:
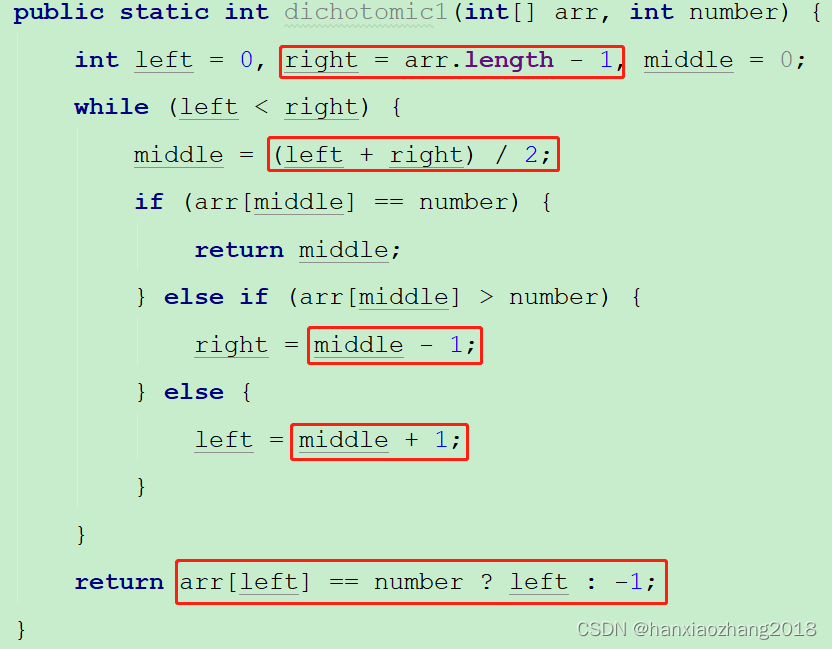
2. 回溯法:
概念:回溯法也称为试探法,是一种选优搜索法,按选优条件向前搜索,以达到目标。但当搜索到某一步时,发现原先选择并不优或者达不到目标,就回退一步重新选择。这种走不通就退回再走的技术就是回溯法。背

N皇后问题:
- 软考使用一维数组存储答案:
- q[n+1] (数组1位置表示第1行皇后存储的列号,数组2位置表示第2行皇后存储的列号)
- 判断两个皇后在同一列:
- Qi 的列号 == Qj的列号 (Qi 表示第i个皇后、Qj表示第j个皇后)
- 判断两个皇后在同一斜线:
- abs(Qi行 - Qj行) == (Qi列 - Qj列)
- 判断皇后没有超过棋盘:
- q[j]
- 判断皇后是否找到最后一列:
- j == n ( j:表示正在摆放第j个皇后)
- 回溯:
- 将还原第j个皇后的位置为0:q[j] = 0
- 回溯到上一个j:j = j - 1
3. 贪心法:
- 概念:总是做出当前来说最好的选择,而并不从整体上加以考虑,它所做的每步选择只是当前步骤的局部最优选择,但从整体来说不一定是最优的选择。由于它不必为了寻找最优解而穷尽所以可能解,因此,其耗费时间少,一般可以快速得到满意的解,但得不到最优解。
- 背包问题:
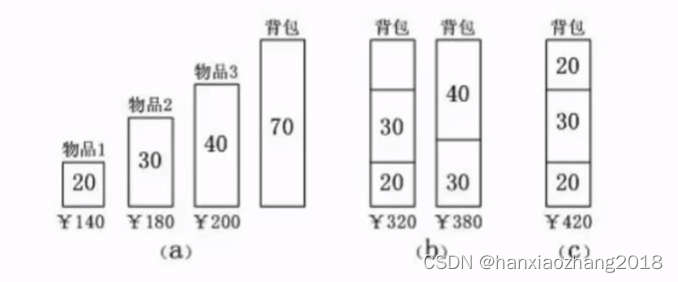
4. 动态规划法:
- 概念:在求解问题中,对于每一步决策,列出各种可能的局部解,再依据某种判定条件,舍弃那些肯定不能得到最优的局部解,在每一步都进过刷选,以每一步都是最优解来保证全局是最优解。

0-1背包问题:

确认子问题范围,画出表格:
- 行 i:0~4 ,列 j: 0~5,其中:i -> 物品数量 j -> 背包容量。
- 表中每个单元代表:从前 i 个物品中选,背包容量为 j 时的最大价值。
公式:
- 物品价值和物品重量数组
// 物品价值 - 索引0位置不用 int[] v = new int[]{0, 2, 4, 5, 6}; // 物品重量 - 索引0位置不用 int[] w = new int[]{0, 1, 2, 3, 4};
- "不选第 i 个 物品" = 从前 i -1 个物品中选,背包容量为 j 时的最大值。
int not = f[i][j] = f[i - 1][j]
- "选择第 i 个物品" = 第 i 个物品的价值 + 从前 i - 1 个物品中选,背包容量为"j - 第 i 个物品的质量"时的最大价值。 前提条件:背包容量 j 大于等于 第 i 个物品的重量才能选。
int yes = 0 // 背包容量j 等于 第i个物品的重量时,当前最大价值 = 第i物品的价值 if(j == w[i]){ yes = f[i] [j] = v[i] } // 背包容量j 大于 第i个物品的重量时,当前最大价值 = 第i物品的价值 + // 从前i-1个物品中选,背包容量为"j -第i个物品的质量"时的最大价值 if(j > w[ i ]){ yes = f[i] [j] = v[i] + f[i - 1][j -w[i]] }
- 从前 i 个物品中选,背包容量为 j 时的最大价值 = "不选第 i 个 物品" 和 "选择第 i 个物品" 两者的最大值
f[i][j] = max(not,yes)
5. C语言语法:
- return 0 ; 返回假 return 1 ; 返回真
答题技巧:
- 先处理除补全代码以外的题,再填写代码。
例题1:




问题1:
(1) j=0 (2) b[j] = b[j] + s[i] (3) min =temp (4) b[m] = b[m] + s[i]

问题2:
(5)贪心算法 (6)贪心算法 (7)O(n²) (8)O(n²)
问题3:
(9)

(10)
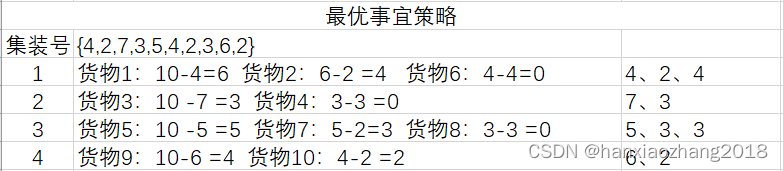
(11)不能得到最优解, 这里的都是使用的贪心策略。
例题2:

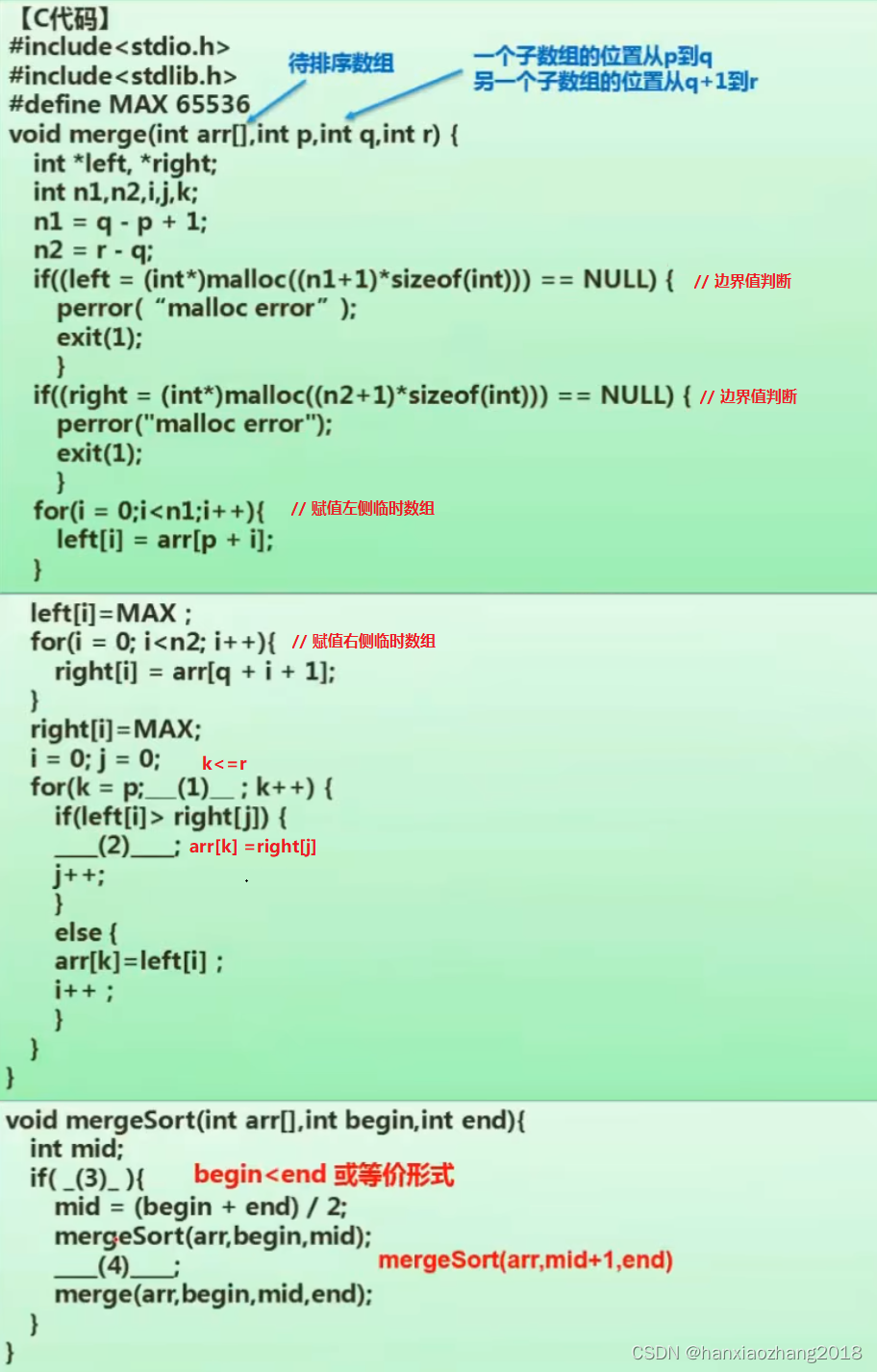

问题1:
(1)k
首先,函数void merge(int arr[],int p,int q,int r)的意思是:对子数组 arr[p...q]和子数组 arr[q+1...r]进行合并。
因此,第一空为k当数组长度为1时,停止递归,因为此时该数组有序,则第三空为 begin
合并了begin到mid之间的元素,继续合并mid+1到end之间的元素,则第四空为 mergeSort(arr,mid+1,end)。
问题2:
(5) 分治法 (6)T(n) =2T(n/2) +O(n) (7) O(nlogn)(8)O(n)
归并算法实际上就是将数组一直往下分割,直到分割到由一个元素组成的n个子数组,再往上两两归并。将数组进行分割需要logN 步,因为每次都是讲数组分割成两半(2x= N,x = logN)。合并N个元素,需要进行N步,也就是O(N),则总的时间复杂度为 O(NlogN)。
合并过程中,使用了n个中间变量存储,left = (int*)malloc((n1+1)*sizeof(int))。所以空间复杂度为 O(n)。
递归式 todo 不会
推导递归式: 假设n个元素进行归并排序需要T(n),可以将其分割成两个分别有n/2个元素的数组分别进行归并,也就是 2T(n/2),在将这两个合并,需要 O(n)的时间复杂度。则推导公式为 T(n) = 2T(n/2)+o(n)。
问题3:
n1+ n2