例题一

解法(动态规划):
算法思路:
1. 状态表⽰:
对于简单的线性 dp ,我们可以⽤「经验 + 题⽬要求」来定义状态表⽰:
i. 以某个位置为结尾,巴拉巴拉;
ii. 以某个位置为起点,巴拉巴拉。
这⾥我们选择⽐较常⽤的⽅式,以某个位置为结尾,结合题⽬要求,定义⼀个状态表⽰:
dp[i] 表⽰:选择到 i 位置时,此时的最⻓预约时⻓。但是我们这个题在 i 位置的时候,会⾯临「选择」或者「不选择」两种抉择,所依赖的状态需要细分:
▪ f[i] 表⽰:选择到 i 位置时, nums[i] 必选,此时的最⻓预约时⻓;
▪ g[i] 表⽰:选择到 i 位置时, nums[i] 不选,此时的最⻓预约时⻓。
2. 状态转移⽅程: 因为状态表⽰定义了两个,因此我们的状态转移⽅程也要分析两个:
对于f[i] :
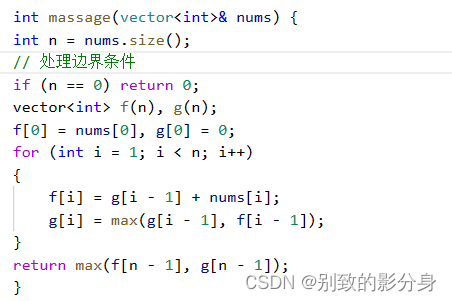
▪ 如果 nums[i] 必选,那么我们仅需知道 i - 1 位置在不选的情况下的最⻓预约时⻓,然后加上 nums[i] 即可,因此 f[i] = g[i - 1] + nums[i] 。
对于 g[i] :
▪ 如果 nums[i] 不选,那么 i - 1 位置上选或者不选都可以。因此,我们需要知道 i - 1 位置上选或者不选两种情况下的最⻓时⻓,因此 g[i] = max(f[i - 1], g[i - 1]) 。
3. 初始化:
这道题的初始化⽐较简单,因此⽆需加辅助节点,仅需初始化 f[0] = nums[0], g[0] = 0即可。
4. 填表顺序
根据「状态转移⽅程」得「从左往右,两个表⼀起填」。
5. 返回值根据「状态表⽰」,应该返回 max(f[n - 1], g[n - 1]) 。
例题二

解法(动态规划)
算法思路:
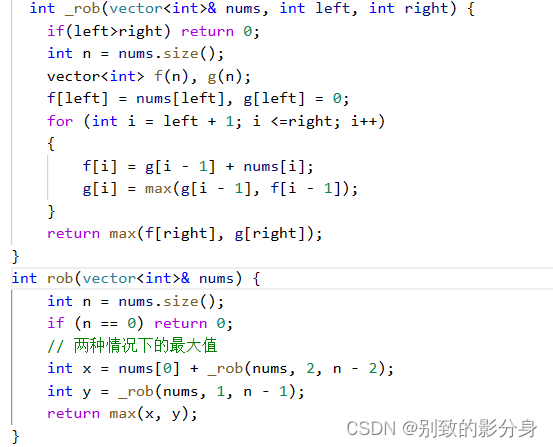
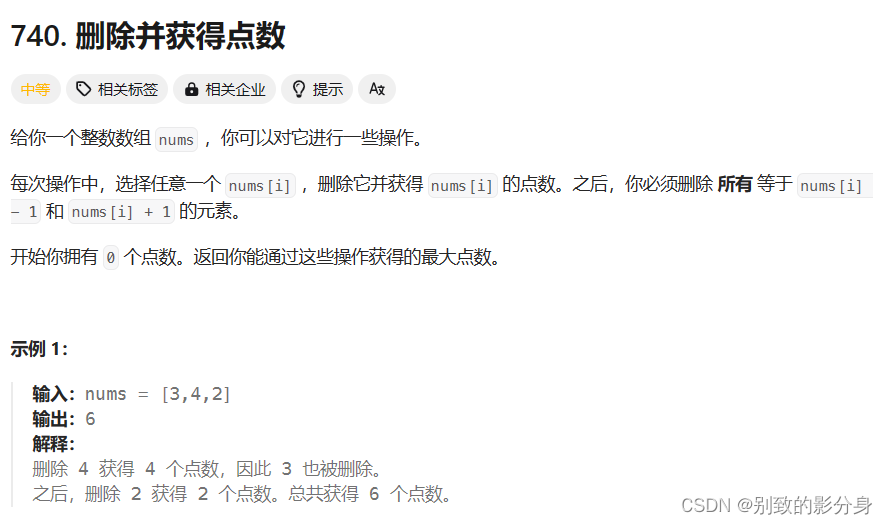
这⼀个问题是「打家劫舍I」问题的变形。
上⼀个问题是⼀个「单排」的模式,这⼀个问题是⼀个「环形」的模式,也就是⾸尾是相连的。但
是我们可以将「环形」问题转化为「两个单排」问题:
a. 偷第⼀个房屋时的最⼤⾦额 x ,此时不能偷最后⼀个房⼦,因此就是偷 [0, n - 2] 区间的房⼦;
b. 不偷第⼀个房屋时的最⼤⾦额 y ,此时可以偷最后⼀个房⼦,因此就是偷 [1, n - 1] 区间的房⼦;
两种情况下的「最⼤值」,就是最终的结果。因此,问题就转化成求「两次单排结果的最⼤值」。
例题三
解法(动态规划):
算法思路:
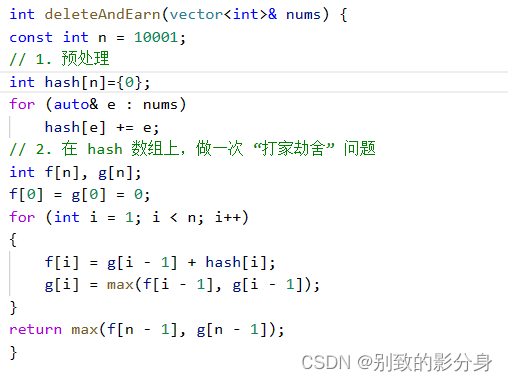
其实这道题依旧是「打家劫舍I」问题的变型。我们注意到题⽬描述,选择 x 数字的时候, x - 1 与 x + 1 是不能被选择的。像不像「打家劫舍」问题中,选择 i 位置的⾦额之后,就不能选择 i - 1 位置以及 i + 1 位置的⾦额呢~ 因此,我们可以创建⼀个⼤⼩为 10001 (根据题⽬的数据范围)的 hash 数组,将 nums 数组中每⼀个元素 x ,累加到 hash 数组下标为 x 的位置处,然后在 hash 数组上来⼀次「打家劫舍」即可。
例题四

解法(动态规划):
算法思路:
1. 状态表⽰:
对于线性 dp ,我们可以⽤「经验 + 题⽬要求」来定义状态表⽰:
i. 以某个位置为结尾,巴拉巴拉;
ii. 以某个位置为起点,巴拉巴拉。
这⾥我们选择⽐较常⽤的⽅式,以某个位置为结尾,结合题⽬要求,定义⼀个状态表⽰: 但是我们这个题在 i 位置的时候,会⾯临「红」「蓝」「绿」三种抉择,所依赖的状态需要细分:
▪ dp[i][0] 表⽰:粉刷到 i 位置的时候,最后⼀个位置粉刷上「红⾊」,此时的最⼩花费;
▪ dp[i][1] 表⽰:粉刷到 i 位置的时候,最后⼀个位置粉刷上「蓝⾊」,此时的最⼩花费;
▪ dp[i][2] 表⽰:粉刷到 i 位置的时候,最后⼀个位置粉刷上「绿⾊」,此时的最⼩花费。
2. 状态转移⽅程:
因为状态表⽰定义了三个,因此我们的状态转移⽅程也要分析三个:
对于 dp[i][0] :
▪ 如果第 i 个位置粉刷上「红⾊」,那么 i - 1 位置上可以是「蓝⾊」或者「绿⾊」。因此我们
需要知道粉刷到 i - 1 位置上的时候,粉刷上「蓝⾊」或者「绿⾊」的最⼩花费,然后加上 i
位置的花费即可。于是状态转移⽅程为: dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i - 1][0] ;
同理,我们可以推导出另外两个状态转移⽅程为:
dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i - 1][1] ;
dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + costs[i - 1][2] 。
3. 初始化:
可以在最前⾯加上⼀个「辅助结点」,帮助我们初始化。使⽤这种技巧要注意两个点:
i. 辅助结点⾥⾯的值要「保证后续填表是正确的」;
ii. 「下标的映射关系」。
在本题中,添加⼀个节点,并且初始化为 0 即可。
4. 填表顺序
根据「状态转移⽅程」得「从左往右,三个表⼀起填」。
5. 返回值
根据「状态表⽰」,应该返回最后⼀个位置粉刷上三种颜⾊情况下的最⼩值,因此需要返回:
min(dp[n][0], min(dp[n][1], dp[n][2])) 。

例题五

解法(动态规划):
算法思路:
1. 状态表⽰:
对于线性 dp ,我们可以⽤「经验 + 题⽬要求」来定义状态表⽰:
i. 以某个位置为结尾,巴拉巴拉;
ii. 以某个位置为起点,巴拉巴拉。
这⾥我们选择⽐较常⽤的⽅式,以某个位置为结尾,结合题⽬要求,定义⼀个状态表⽰:
由于有「买⼊」「可交易」「冷冻期」三个状态,因此我们可以选择⽤三个数组,其中:
▪ dp[i][0] 表⽰:第 i 天结束后,处于「买⼊」状态,此时的最⼤利润;
▪ dp[i][1] 表⽰:第 i 天结束后,处于「可交易」状态,此时的最⼤利润;
▪ dp[i][2] 表⽰:第 i 天结束后,处于「冷冻期」状态,此时的最⼤利润。
2. 状态转移⽅程:
我们要谨记规则:
i. 处于「买⼊」状态的时候,我们现在有股票,此时不能买股票,只能继续持有股票,或者卖
出股票;
ii. 处于「卖出」状态的时候:
• 如果「在冷冻期」,不能买⼊;
• 如果「不在冷冻期」,才能买⼊。
◦ 对于 dp[i][0] ,我们有「两种情况」能到达这个状态:
i. 在 i - 1 天持有股票,此时最⼤收益应该和 i - 1 天的保持⼀致: dp[i - 1] [0] ;
ii. 在 i 天买⼊股票,那我们应该选择 i - 1 天不在冷冻期的时候买⼊,由于买⼊需要花钱,所以此时最⼤收益为: dp[i - 1][1] - prices[i] 两种情况应取最⼤值,因此:
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]) 。
◦ 对于 dp[i][1] ,我们有「两种情况」能到达这个状态:
i. 在 i - 1 天的时候,已经处于冷冻期,然后啥也不⼲到第 i 天,此时对应的状态为: dp[i - 1][2] ;
ii. 在 i - 1 天的时候,⼿上没有股票,也不在冷冻期,但是依旧啥也不⼲到第 i 天,此时对应的状态为 dp[i - 1][1] ;两种情况应取最⼤值,因此: dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]) 。
◦ 对于 dp[1][i] ,我们只有「⼀种情况」能到达这个状态:
i. 在 i - 1 天的时候,卖出股票。 因此对应的状态转移为: dp[i][2] = dp[i - 1][0] + prices[i] 。
3. 初始化:
三种状态都会⽤到前⼀个位置的值,因此需要初始化每⼀⾏的第⼀个位置:
dp[0][0] :此时要想处于「买⼊」状态,必须把第⼀天的股票买了,因此 dp[0][0] = - prices[0] ;
dp[0][1] :啥也不⽤⼲即可,因此 dp[0][1] = 0 ;
dp[0][2] :⼿上没有股票,买⼀下卖⼀下就处于冷冻期,此时收益为 0 ,因此 dp[0][2] = 0 。
4. 填表顺序:
根据「状态表⽰」,我们要三个表⼀起填,每⼀个表「从左往右」。
5. 返回值:
应该返回「卖出状态」下的最⼤值,因此应该返回 max(dp[n - 1][1], dp[n - 1] [2]) 。

例题六

解法(动态规划):
算法思路:
1. 状态表⽰:
对于线性 dp ,我们可以⽤「经验 + 题⽬要求」来定义状态表⽰:
i. 以某个位置为结尾,巴拉巴拉;
ii. 以某个位置为起点,巴拉巴拉。
这⾥我们选择⽐较常⽤的⽅式,以某个位置为结尾,结合题⽬要求,定义⼀个状态表⽰:
由于有「买⼊」「可交易」两个状态,因此我们可以选择⽤两个数组,其中:
▪ f[i] 表⽰:第 i 天结束后,处于「买⼊」状态,此时的最⼤利润;
▪ g[i] 表⽰:第 i 天结束后,处于「卖出」状态,此时的最⼤利润。
2. 状态转移⽅程:
我们选择在「卖出」的时候,⽀付这个⼿续费,那么在「买⼊」的时候,就不⽤再考虑⼿续费的问
题。
◦ 对于 f[i] ,我们有两种情况能到达这个状态:
i. 在 i - 1 天「持有」股票,第 i 天啥也不⼲。此时最⼤收益为 f[i - 1] ;
ii. 在 i - 1 天的时候「没有」股票,在第 i 天买⼊股票。此时最⼤收益为 g[i - 1] - prices[i]) ;
两种情况下应该取最⼤值,因此 f[i] = max(f[i - 1], g[i - 1] - prices[i]) 。
◦ 对于 g[i] ,我们也有两种情况能够到达这个状态:
i. 在 i - 1 天「持有」股票,但是在第 i 天将股票卖出。此时最⼤收益为: f[i - 1] + prices[i] - fee) ,记得⼿续费;
ii. 在 i - 1 天「没有」股票,然后第 i 天啥也不⼲。此时最⼤收益为: g[i - 1] ;
两种情况下应该取最⼤值,因此 g[i] = max(g[i - 1], f[i - 1] + prices[i] - fee) 。
3. 初始化:
由于需要⽤到前⾯的状态,因此需要初始化第⼀个位置。
◦ 对于 f[0] ,此时处于「买⼊」状态,因此 f[0] = -prices[0] ;
◦ 对于 g[0] ,此时处于「没有股票」状态,啥也不⼲即可获得最⼤收益,因此 g[0] = 0 。
4. 填表顺序:
毫⽆疑问是「从左往右」,但是两个表需要⼀起填。
5. 返回值:
应该返回「卖出」状态下,最后⼀天的最⼤值收益: g[n - 1] 。

例题七

解法(动态规划):
算法思路:
1. 状态表⽰:
对于线性 dp ,我们可以⽤「经验 + 题⽬要求」来定义状态表⽰:
i.
以某个位置为结尾,巴拉巴拉;
ii.
以某个位置为起点,巴拉巴拉。
这⾥我们选择⽐较常⽤的⽅式,以某个位置为结尾,结合题⽬要求,定义⼀个状态表⽰:
由于有「买⼊」「可交易」两个状态,因此我们可以选择⽤两个数组。但是这道题⾥⾯还有交易次
数的限制,因此我们还需要再加上⼀维,⽤来表⽰交易次数。其中:▪
f[i][j]
表⽰:第
i
天结束后,完成了
j
次交易,处于「买⼊」状态,此时的最⼤利
润;
▪
g[i][j]
表⽰:第
i
天结束后,完成了
j
次交易,处于「卖出」状态,此时的最⼤利
润。
2.
状态转移⽅程:
对于
f[i][j] ,我们有两种情况到这个状态:
i.
在 i - 1 天的时候,交易了
j
次,处于「买⼊」状态,第
i
天啥也不⼲即可。此时最
⼤利润为: f[i - 1][j] ;
ii. 在 i - 1 天的时候,交易了
j
次,处于「卖出」状态,第
i
天的时候把股票买了。此
时的最⼤利润为: g[i - 1][j] - prices[i] 。
综上,我们要的是「最⼤利润」,因此是两者的最⼤值: f[i][j] = max(f[i - 1][j],
g[i - 1][j] - prices[i]) 。
对于
g[i][j] ,我们也有两种情况可以到达这个状态:
i.
在 i - 1 天的时候,交易了 j 次,处于「卖出」状态,第 i 天啥也不⼲即可。此时的
最⼤利润为: g[i - 1][j] ;
ii. 在 i - 1 天的时候,交易了 j - 1 次,处于「买⼊」状态,第 i 天把股票卖了,然
后就完成了 j ⽐交易。此时的最⼤利润为: f[i - 1][j - 1] + prices[i] 。但
是这个状态不⼀定存在,要先判断⼀下。
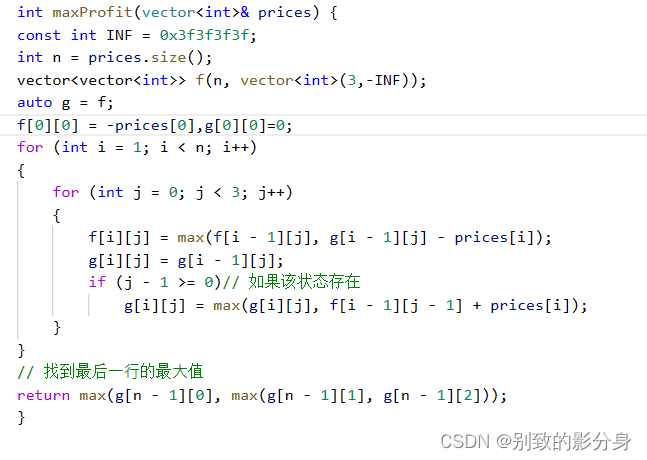
综上,我们要的是最⼤利润,因此状态转移⽅程为:
g[i][j] = g[i - 1][j];
if(j >= 1) g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
3.
初始化:
由于需要⽤到 i = 0 时的状态,因此我们初始化第⼀⾏即可。
◦
当处于第 0 天的时候,只能处于「买⼊过⼀次」的状态,此时的收益为 -prices[0] ,因
此 f[0][0] = - prices[0] 。
◦
为了取 max 的时候,⼀些不存在的状态「起不到⼲扰」的作⽤,我们统统将它们初始化为 -
INF (⽤ INT_MIN 在计算过程中会有「溢出」的⻛险,这⾥ INF 折半取
0x3f3f3f3f ,⾜够⼩即可)
4.
填表顺序:从「上往下填」每⼀⾏,每⼀⾏「从左往右」,两个表「⼀起填」。
5. 返回值:
返回处于「卖出状态」的最⼤值,但是我们也「不知道是交易了⼏次」,因此返回 g 表最后⼀⾏
的最⼤值。
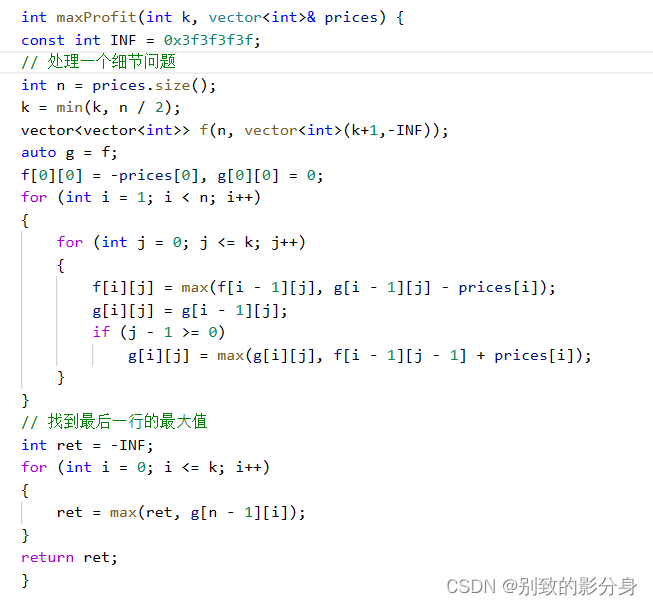
例题八

解法(动态规划):
算法思路:
1. 状态表⽰:
为了更加清晰的区分「买⼊」和「卖出」,我们换成「有股票」和「⽆股票」两个状态。
f[i][j] 表⽰:第 i 天结束后,完成了 j 笔交易,此时处于「有股票」状态的最⼤收益;
g[i][j] 表⽰:第 i 天结束后,完成了 j 笔交易,此时处于「⽆股票」状态的最⼤收益。
2. 状态转移⽅程: 对于 f [i][j] ,我们也有两种情况能在第 i 天结束之后,完成 j 笔交易,此时⼿⾥「有股票」的状态:
i. 在 i - 1 天的时候,⼿⾥「有股票」,并且交易了 j 次。在第 i 天的时候,啥也不⼲。此时的收益为 f[i - 1][j] ;
ii. 在 i - 1 天的时候,⼿⾥「没有股票」,并且交易了 j 次。在第 i 天的时候,买了股票。那么 i 天结束之后,我们就有股票了。此时的收益为 g[i - 1][j] - prices[i] ;
上述两种情况,我们需要的是「最⼤值」,因此 f 的状态转移⽅程为:
f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i])
对于 g [i][j] ,我们有下⾯两种情况能在第 i 天结束之后,完成 j 笔交易,此时⼿⾥「没有
股票」的状态:
i. 在 i - 1 天的时候,⼿⾥「没有股票」,并且交易了 j 次。在第 i 天的时候,啥也不⼲。此时的收益为 g[i - 1][j] ;
ii. 在 i - 1 天的时候,⼿⾥「有股票」,并且交易了 j - 1 次。在第 i 天的时候,把股票卖了。那么 i 天结束之后,我们就交易了 j 次。此时的收益为 f[i - 1][j - 1] + prices[i] ;
上述两种情况,我们需要的是「最⼤值」,因此 g 的状态转移⽅程为:
g[i][j] = max(g[i - 1][j], f[i - 1][j - 1] + prices[i])
3. 初始化:
由于需要⽤到 i = 0 时的状态,因此我们初始化第⼀⾏即可。
◦ 当处于第 0 天的时候,只能处于「买⼊过⼀次」的状态,此时的收益为 -prices[0] ,因此
f[0][0] = - prices[0] 。
◦ 为了取 max 的时候,⼀些不存在的状态「起不到⼲扰」的作⽤,我们统统将它们初始化为
- INF (⽤ INT_MIN 在计算过程中会有「溢出」的⻛险,这⾥ INF 折半取0x3f3f3f3f ,⾜够⼩即可)
4. 填表顺序:
从上往下填每⼀⾏,每⼀⾏从左往右,两个表⼀起填。
5. 返回值:
返回处于卖出状态的最⼤值,但是我们也不知道是交易了⼏次,因此返回 g 表最后⼀⾏的最⼤
值。
优化点:
我们的交易次数是不会超过整个天数的⼀半的,因此我们可以先把 k 处理⼀下,优化⼀下问题的规
模: k = min(k, n / 2)