self-attention 的 CUDA 实现及优化 (上)
导 读
self-attention 是 Transformer 中最关键、最复杂的部分,也是 Transformer 优化的核心环节。理解 self-attention ,对于深入理解 Transformer 具有关键作用,本篇主要就围绕 self-attention 展开,由于该部分比较复杂,故分为上下两篇,本篇为上篇。
0****1
self-attention的CUDA简单实现
self-attention 的原理非常常见,在之前的文章中也分析很多,因此不在此介绍介绍其原理,仅解读代码。
1、CPU版本
以下是基础的 CPU 版本的实现,下面对其稍作分析:
• 输入inp 为 x 与 QKV_weight 相乘后得到的 QKV 值,对于b(batch size), t(sequence len), h(head) 的 q(query_t) 值的索引为 inp[b,t,h*hs:(h+1)hs] , k(key_t2) 值在此基础上偏移 C 维即可,即inp[b,t,h*hs+C:(h+1)hs+C]
• 得到 q,k 之后,便通过点乘计算 attention 值,算完一个 attn 值之后进行 scale 操作(同时记录最大值以便进行softmax),计算完一行后进行 mask 操作
• 进行 softmax 操作,得到 attn 值
• 索引 v(value_t2) 并与 attn 值进行矩阵乘法运算
// CPU code reference
void attention_forward_cpu(float* out, float* preatt, float* att,
const float* inp,
int B, int T, int C, int NH) {
// input is (B, T, 3C) Q,K,V
// preatt, att are (B, NH, T, T)
// output is (B, T, C)
int C3 = C*3;
int hs = C / NH; // head size
float scale = 1.0 / sqrtf(hs);
for (int b = 0; b < B; b++) {
for (int t = 0; t < T; t++) {
for (int h = 0; h < NH; h++) {
const float* query_t = inp + b * T * C3 + t * C3 + h * hs;
float* preatt_bth = preatt + b*NH*T*T + h*T*T + t*T;
float* att_bth = att + b*NH*T*T + h*T*T + t*T;
// pass 1: calculate query dot key and maxval
float maxval = -10000.0f; // TODO something better
for (int t2 = 0; t2 <= t; t2++) {
const float* key_t2 = inp + b * T * C3 + t2 * C3 + h * hs + C; // +C because it's key
// (query_t) dot (key_t2)
float val = 0.0f;
for (int i = 0; i < hs; i++) {
val += query_t[i] * key_t2[i];
}
val *= scale;
if (val > maxval) {
maxval = val;
}
preatt_bth[t2] = val;
}
// pad with -INFINITY outside of autoregressive region for debugging comparisons
for (int t2 = t+1; t2 < T; t2++) {
preatt_bth[t2] = -INFINITY;
}
// pass 2: calculate the exp and keep track of sum
float expsum = 0.0f;
for (int t2 = 0; t2 <= t; t2++) {
float expv = expf(preatt_bth[t2] - maxval);
expsum += expv;
att_bth[t2] = expv;
}
float expsum_inv = expsum == 0.0f ? 0.0f : 1.0f / expsum;
// pass 3: normalize to get the softmax
for (int t2 = 0; t2 < T; t2++) {
if (t2 <= t) {
att_bth[t2] *= expsum_inv;
} else {
// causal attention mask. not strictly necessary to set to zero here
// only doing this explicitly for debugging and checking to PyTorch
att_bth[t2] = 0.0f;
}
}
// pass 4: accumulate weighted values into the output of attention
float* out_bth = out + b * T * C + t * C + h * hs;
for (int i = 0; i < hs; i++) { out_bth[i] = 0.0f; }
for (int t2 = 0; t2 <= t; t2++) {
const float* value_t2 = inp + b * T * C3 + t2 * C3 + h * hs + C*2; // +C*2 because it's value
float att_btht2 = att_bth[t2];
for (int i = 0; i < hs; i++) {
out_bth[i] += att_btht2 * value_t2[i];
}
}
}
}
}
}
2、CUDA初步实现(V1)
仍然延续 CPU 版本的基本思路,只是计算的不同,拆分为 3 个 kernel 进行计算:
• 第一步:计算 attention 值,总共使用B*NH*T*T 个线程,即每个线程计算一个值
// attention calculation
int total_threads = B * NH * T * T;
int num_blocks = ceil_div(total_threads, block_size);
attention_query_key_kernel1<<<num_blocks, block_size>>>(preatt, inp, B, T, C, NH);
kernel 函数的实现如下:
__global__ void attention_query_key_kernel1(float* preatt, const float* inp,
int B, int T, int C, int NH) {
int idx = blockIdx.x * blockDim.x + threadIdx.x;
int total_threads = B * NH * T * T;
if (idx < total_threads) {
int t2 = idx % T;
int t = (idx / T) % T;
if (t2 > t) {
// autoregressive mask
preatt[idx] = -INFINITY;
return;
}
int h = (idx / (T * T)) % NH;
int b = idx / (NH * T * T);
int C3 = C*3;
int hs = C / NH; // head size
const float* query_t = inp + b * T * C3 + t * C3 + h * hs;
const float* key_t2 = inp + b * T * C3 + t2 * C3 + h * hs + C; // +C because it's key
// (query_t) dot (key_t2)
float val = 0.0f;
for (int i = 0; i < hs; i++) {
val += query_t[i] * key_t2[i];
}
val *= 1.0 / sqrtf(hs);
preatt[idx] = val;
}
}
• 第二步:softmax 操作,该操作在之前的 op 优化中已经详细讨论,不予赘述
_global__ void attention_softmax_kernel1(float* att, const float* preatt,
int B, int T, int NH) {
int idx = blockIdx.x * blockDim.x + threadIdx.x;
int total_threads = B * T * NH;
if (idx < total_threads) {
int h = idx % NH;
int t = (idx / NH) % T;
int b = idx / (NH * T);
const float* preatt_bth = preatt + b*NH*T*T + h*T*T + t*T;
float* att_bth = att + b*NH*T*T + h*T*T + t*T;
// find maxval
float maxval = -10000.0f; // TODO something better
for (int t2 = 0; t2 <= t; t2++) {
if (preatt_bth[t2] > maxval) {
maxval = preatt_bth[t2];
}
}
// calculate the exp and keep track of sum
float expsum = 0.0f;
for (int t2 = 0; t2 <= t; t2++) {
float expv = expf(preatt_bth[t2] - maxval);
expsum += expv;
att_bth[t2] = expv;
}
float expsum_inv = expsum == 0.0f ? 0.0f : 1.0f / expsum;
// normalize to get the softmax
for (int t2 = 0; t2 < T; t2++) {
if (t2 <= t) {
att_bth[t2] *= expsum_inv;
} else {
// causal attention mask. not strictly necessary to set to zero here
// only doing this explicitly for debugging and checking to PyTorch
att_bth[t2] = 0.0f;
}
}
}
}
• 第三步:attention 值与 v 进行矩阵乘法运算
__global__ void attention_value_kernel1(float* out, const float* att, const float* inp,
int B, int T, int C, int NH) {
int idx = blockIdx.x * blockDim.x + threadIdx.x;
int total_threads = B * T * NH;
if (idx < total_threads) {
int h = idx % NH;
int t = (idx / NH) % T;
int b = idx / (NH * T);
int C3 = C*3;
int hs = C / NH; // head size
float* out_bth = out + b * T * C + t * C + h * hs;
const float* att_bth = att + b*NH*T*T + h*T*T + t*T;
for (int i = 0; i < hs; i++) { out_bth[i] = 0.0f; }
for (int t2 = 0; t2 <= t; t2++) {
const float* value_t2 = inp + b * T * C3 + t2 * C3 + h * hs + C*2; // +C*2 because it's value
float att_btht2 = att_bth[t2];
for (int i = 0; i < hs; i++) {
out_bth[i] += att_btht2 * value_t2[i];
}
}
}
}
由此完成最基本的 self-attention 的实现,性能数据如下:
block_size 32 | time 238.912872 ms
block_size 64 | time 252.689301 ms
block_size 128 | time 246.945175 ms
block_size 256 | time 261.469421 ms
block_size 512 | time 241.190613 ms
3、flash attention的简单实现(V2)
flash attention 是根据 GPU 的内存体系对 self-attention 做的一个极其重要的优化。

• 首先对于关键参数进行初始化
// these are hardcoded to 32 for now
const int Bc = 32;
const int Br = 32;
// renaming these to be consistent with the kernel
// const int B = B;
const int nh = NH;
const int N = T;
const int d = C / NH;
// more
const int Tc = ceil((float) N / Bc);
const int Tr = ceil((float) N / Br);
const float softmax_scale = 1.0 / sqrt(d);
• 然后计算每个 block 所需要的 SRAM,以确保不会溢出
// calculate SRAM size needed per block, ensure we have enough shared memory
int col_tile_size = Bc * d; // size of Kj, Vj
int row_tile_size = Br * d; // size of Qi
const int sram_size =
(2 * col_tile_size * sizeof(float)) // SRAM size for Kj, Vj
+ (row_tile_size * sizeof(float)) // SRAM size for Qi
+ (Bc * Br * sizeof(float)); // SRAM size for S
int max_sram_size;
cudaDeviceGetAttribute(&max_sram_size, cudaDevAttrMaxSharedMemoryPerBlock, 0);
if (sram_size > max_sram_size) {
printf("Max shared memory: %d, requested shared memory: %d \n", max_sram_size, sram_size);
printf("SRAM size exceeds maximum shared memory per block\n");
printf("Try decreasing col_tile_size or row_tile_size further\n");
exit(1);
}
• 为了避免在 flash attention 中进行复杂的索引、reshape 及 permute 操作,首先使用一个kernel 完成这些操作
__global__ void permute_kernel(float* q, float* k, float* v,
const float* inp,
int B, int N, int NH, int d) {
// okay so now, this kernel wants Q,K,V to all be of shape (B, NH, N, d)
// but instead, we have a single tensor QKV (inp) of shape (B, N, 3, NH, d)
int idx = blockIdx.x * blockDim.x + threadIdx.x;
// Q[b][nh_][n][d_] = inp[b][n][0][nh_][d_]
if (idx < B * NH * N * d) {
int b = idx / (NH * N * d);
int rest = idx % (NH * N * d);
int nh_ = rest / (N * d);
rest = rest % (N * d);
int n = rest / d;
int d_ = rest % d;
int inp_idx = \
(b * N * 3 * NH * d)
+ (n * 3 * NH * d)
+ (0 * NH * d)
+ (nh_ * d)
+ d_;
q[idx] = inp[inp_idx];
k[idx] = inp[inp_idx + NH * d];
v[idx] = inp[inp_idx + 2 * (NH * d)];
}
}
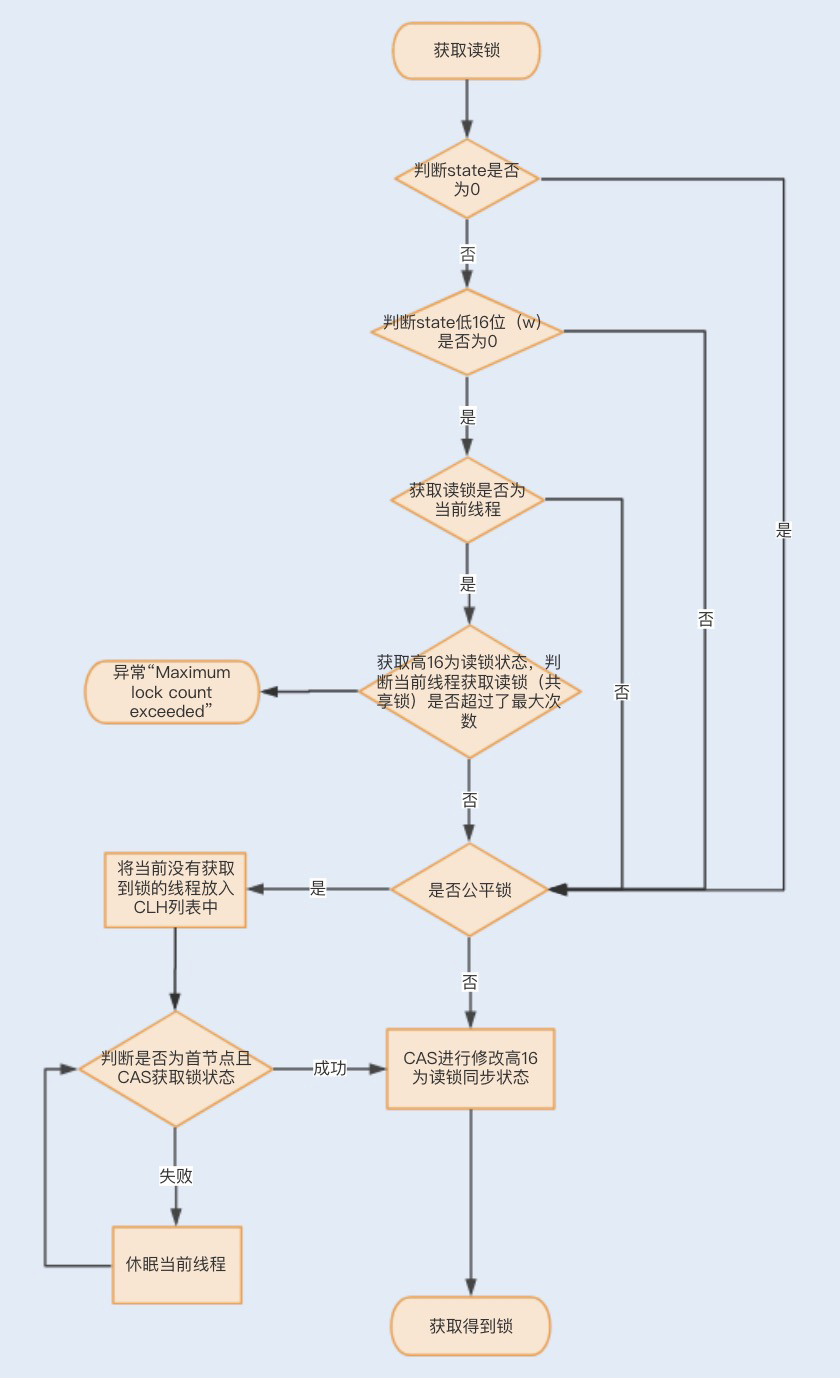
• 之后就是核心环节,flash attention 的实现了,其过程可以参照以下图示:


__global__ void attention_forward_kernel2(
const float* Q,
const float* K,
const float* V,
const int N,
const int d,
const int Tc,
const int Tr,
const int Bc,
const int Br,
const float softmax_scale,
float* l,
float* m,
float* O
) {
int tx = threadIdx.x;
int bx = blockIdx.x; int by = blockIdx.y; // batch and head index
// Offset into Q,K,V,O,l,m - different for each batch and head
int qkv_offset = (bx * gridDim.y * N * d) + (by * N * d); // gridDim.y = nh
int lm_offset = (bx * gridDim.y * N) + (by * N); // offset for l and m
// Define SRAM for Q,K,V,S
extern __shared__ float sram[];
int tile_size = Bc * d; // size of Qi, Kj, Vj
float* Qi = sram;
float* Kj = &sram[tile_size];
float* Vj = &sram[tile_size * 2];
float* S = &sram[tile_size * 3];
for (int j = 0; j < Tc; j++) {
// Load Kj, Vj to SRAM
for (int x = 0; x < d; x++) {
Kj[(tx * d) + x] = K[qkv_offset + (tile_size * j) + (tx * d) + x];
Vj[(tx * d) + x] = V[qkv_offset + (tile_size * j) + (tx * d) + x];
}
__syncthreads(); // such that the inner loop can use the correct Kj, Vj
for (int i = 0; i < Tr; i++) {
// if past the end of the sequence, break
if (i * Br + tx >= N) {
break;
}
// Load Qi to SRAM, l and m to registers
for (int x = 0; x < d; x++) {
Qi[(tx * d) + x] = Q[qkv_offset + (tile_size * i) + (tx * d) + x];
}
float row_m_prev = m[lm_offset + (Br * i) + tx];
float row_l_prev = l[lm_offset + (Br * i) + tx];
// S = QK^T, row_m = rowmax(S)
// S[tx][y] = Sum_{x = 0}^{d-1} {Qi[tx][x] * Kj[y][x]}
// row_m = Max_{y = 0}^{Bc-1} S[tx][y]
// with causal masking
float row_m = -INFINITY;
for (int y = 0; y < Bc; y++) {
if (j * Bc + y >= N) {
break;
}
float sum = 0;
for (int x = 0; x < d; x++) {
sum += Qi[(tx * d) + x] * Kj[(y * d) + x];
}
sum *= softmax_scale;
if (i * Br + tx < j * Bc + y)
sum = -INFINITY;
S[(Bc * tx) + y] = sum;
if (sum > row_m)
row_m = sum;
}
// implement softmax with causal masking
// P = exp(S - row_m), row_l = rowsum(P)
// P[tx][y] = exp(S[tx][y] - row_m)
float row_l = 0;
for (int y = 0; y < Bc; y++) {
if (j * Bc + y >= N) {
break;
}
if (i * Br + tx < j * Bc + y)
S[(Bc * tx) + y] = 0;
else
S[(Bc * tx) + y] = __expf(S[(Bc * tx) + y] - row_m);
row_l += S[(Bc * tx) + y];
}
// Compute new m and l
float row_m_new = max(row_m_prev, row_m);
float row_l_new = (__expf(row_m_prev - row_m_new) * row_l_prev) + (__expf(row_m - row_m_new) * row_l);
// Write O, l, m to HBM
for (int x = 0; x < d; x++) {
float pv = 0; // Pij * Vj
for (int y = 0; y < Bc; y++) {
if (j * Bc + y >= N) {
break;
}
pv += S[(Bc * tx) + y] * Vj[(y * d) + x];
}
O[qkv_offset + (tile_size * i) + (tx * d) + x] = (1 / row_l_new) \
* ((row_l_prev * __expf(row_m_prev - row_m_new) * O[qkv_offset + (tile_size * i) + (tx * d) + x]) \
+ (__expf(row_m - row_m_new) * pv));
}
m[lm_offset + (Br * i) + tx] = row_m_new;
l[lm_offset + (Br * i) + tx] = row_l_new;
}
__syncthreads(); // otherwise, thread can use the wrong Kj, Vj in inner loop
}
}
• 以上计算完成后,还需要进行 unpermute 操作,具体如下:
__global__ void unpermute_kernel(const float* inp, float *out, int B, int N, int NH, int d) {
// out has shape (B, nh, N, d) but we need to unpermute it to (B, N, nh, d)
int idx = blockIdx.x * blockDim.x + threadIdx.x;
// out[b][n][nh_][d_] <- inp[b][nh_][n][d_]
if (idx < B * NH * N * d) {
int b = idx / (NH * N * d);
int rest = idx % (NH * N * d);
int nh_ = rest / (N * d);
rest = rest % (N * d);
int n = rest / d;
int d_ = rest % d;
int other_idx = (b * NH * N * d) + (n * NH * d) + (nh_ * d) + d_;
out[other_idx] = inp[idx];
}
}
这样就完成了简单的 flash attention 1 的前向过程,性能相较于V1反而有所下降,主要是数据量较小所致,数据如下:
block_size 32 | time 536.709961 ms
block_size 64 | time 526.100098 ms
block_size 128 | time 583.016235 ms
block_size 256 | time 573.955994 ms
block_size 512 | time 534.477051 ms
0****2
self-attention的高效实现
1、 使用 cuBLAS 库函数(V3)
在之前的实现中,所有的操作都是手动实现的,尽管从结果上看完全正确,但是性能上和官方版本仍有较大差距。因此本节将 self-attention 中的矩阵乘法操作使用官方 cuBLAS 库来实现。
在此仅展示两个矩阵乘法的实现过程,首先是q@k.T 如下:
// batched matrix multiply with cuBLAS
const float alpha = 1.0f;
const float beta = 0.0f;
cublasCheck(cublasSgemmStridedBatched(cublas_handle,
CUBLAS_OP_T, CUBLAS_OP_N,
T, T, HS,
&alpha,
k, HS, T * HS,
q, HS, T * HS,
&beta,
preatt, T, T * T,
B * NH));
然后是att@v ,如下:
// new approach: first cuBLAS another batched matmul
// y = att @ v # (B, nh, T, T) @ (B, nh, T, hs) -> (B, nh, T, hs)
cublasCheck(cublasSgemmStridedBatched(cublas_handle,
CUBLAS_OP_N, CUBLAS_OP_N,
HS, T, T,
&alpha,
v, HS, T * HS,
att, T, T * T,
&beta,
vaccum, HS, T * HS,
B * NH));
性能相较于 V1 版本,提升约百倍以上,数据如下:
block_size 32 | time 4.318913 ms
block_size 64 | time 2.606850 ms
block_size 128 | time 2.034935 ms
block_size 256 | time 2.031407 ms
block_size 512 | time 2.064406 ms
2 、算子融合与 online softmax(V4)
在 V3 基础上,使用 online softmax 并且将 scale 操作融合,具体如下:
__global__ void softmax_forward_kernel5(float* out, float inv_temperature, const float* inp, int N, int T) {
// inp, out shape: (N, T, T), where N = B * NH
// fuses the multiplication by scale inside attention
// directly autoregressive, so we only compute the lower triangular part
// uses the online softmax algorithm
assert(T % 4 == 0);
namespace cg = cooperative_groups;
cg::thread_block block = cg::this_thread_block();
cg::thread_block_tile<32> warp = cg::tiled_partition<32>(block);
int idx = blockIdx.x * warp.meta_group_size() + warp.meta_group_rank();
if(idx >= N * T) {
return;
}
int own_pos = idx % T;
int pos_by_4 = own_pos / 4;
// one row of inp, i.e. inp[idx, :] of shape (T,)
const float* x = inp + idx * T;
// not INF, so we don't get NaNs accidentally when subtracting two values.
float maxval = -FLT_MAX;
float sumval = 0.0f;
const float4* x_vec = reinterpret_cast<const float4*>(x);
for (int i = warp.thread_rank(); i < pos_by_4; i += warp.size()) {
float4 v = x_vec[i];
float old_maxval = maxval;
for(int k = 0; k < 4; ++k) {
maxval = fmaxf(maxval, vec_at(v, k));
}
sumval *= expf(inv_temperature * (old_maxval - maxval));
for(int k = 0; k < 4; ++k) {
sumval += expf(inv_temperature * (vec_at(v, k) - maxval));
}
}
if(4*pos_by_4 + warp.thread_rank() <= own_pos) {
float old_maxval = maxval;
maxval = fmaxf(maxval, x[4*pos_by_4 + warp.thread_rank()]);
sumval *= expf(inv_temperature * (old_maxval - maxval));
sumval += expf(inv_temperature * (x[4*pos_by_4 + warp.thread_rank()] - maxval));
}
float global_maxval = cg::reduce(warp, maxval, cg::greater<float>{});
sumval *= expf(inv_temperature * (maxval - global_maxval));
float sum = cg::reduce(warp, sumval, cg::plus<float>{});
float norm = 1.f / sum;
// divide the whole row by the sum
for (int i = warp.thread_rank(); i <= own_pos; i += warp.size()) {
// recalculation is faster than doing the round-trip through memory.
float ev = expf(inv_temperature * (__ldcs(x + i) - global_maxval));
__stcs(out + idx * T + i, ev * norm);
}
}
其余操作不变,性能略有提升,数据如下:
block_size 32 | time 1.198167 ms
block_size 64 | time 1.073088 ms
block_size 128 | time 1.042434 ms
block_size 256 | time 1.041798 ms
block_size 512 | time 1.044009 ms
3 、使用 FP16 进行矩阵运算(V5)
在 permute/unpermute 阶段进行 FP32<->FP16 类型转换,如下:
if (!skip_permute || first_run_validation) {
permute_kernel_lowp<<<num_blocks, block_size>>>(q, k, v, inp, B, T, NH, HS);
}
...
if(!skip_permute || first_run_validation) {
unpermute_kernel_lowp<<<num_blocks, block_size>>>(vaccum, out, B, T, NH, HS);
}
性能数据如下:
block_size 32 | time 0.866851 ms
block_size 64 | time 0.743674 ms
block_size 128 | time 0.703196 ms
block_size 256 | time 0.713902 ms
block_size 512 | time 0.712848 ms
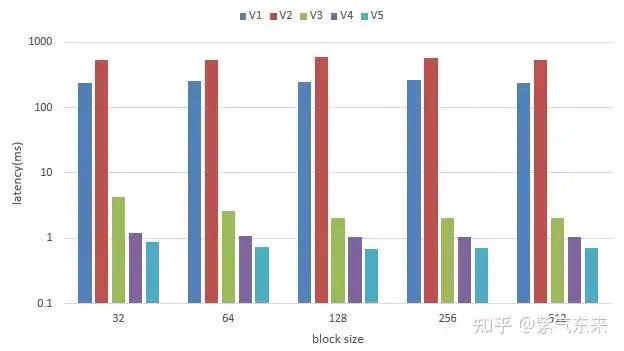
以上几种方法的对比如下,注意坐标轴为指数,计算设备的 A100-80G
![解决Pyppeteer下载chromium慢或者失败的问题[INFO] Starting Chromium download.](https://img-blog.csdnimg.cn/direct/8068d2b209ea41a98c08e9a2888e0079.png)




![[leetcode] 67. 二进制求和](https://img-blog.csdnimg.cn/direct/a36c1b59f2eb48eebd27dc7ba26116ca.png)