通过之前的文章,我们已经基本掌握了R语言的基本使用方法,那从本次教程开始,我们开始聚焦如何使用R语言进行回归建模。
4.1 回归简介
回归分析是一种统计学方法,用于研究两个或多个变量之间的相互关系和依赖程度。它可以帮助我们了解一个或多个自变量(解释变量)如何影响因变量(响应变量)。在回归分析中,通常假设存在某种因果关系,即自变量的变化会导致因变量的变化。
回归分析可以分为多种类型,其中最常见的是线性回归和多项式回归。线性回归试图找到一条直线来最好地拟合数据点,而多项式回归则寻找一个多项式函数来描述变量之间的关系。此外,还有逻辑回归、岭回归、套索回归等不同的回归模型,它们适用于不同类型的数据和分析需求。
在实际应用中,回归分析被广泛使用于预测和建模任务,比如在经济学中预测房价与房屋特征的关系,或者在医学研究中分析疾病发病率与生活习惯的关联。通过构建回归模型,研究者可以估计出特定自变量变化对因变量的影响大小,并据此做出预测。
进行回归分析时,通常会计算一个统计量——决定系数(R²),它表示模型对数据的拟合程度。R²值的范围从0到1,越接近1意味着模型的解释能力越强。然而,高R²值并不总是意味着模型就一定是好的,因为可能存在过拟合问题,即模型过于复杂以至于捕捉到了数据中的噪声而非底层规律。
4.2 OLS回归
普通最小二乘回归(Ordinary Least Squares, OLS)是一种基本的回归分析方法,它广泛应用于经济学、金融学、生物学、市场营销等多个领域。OLS回归的核心思想是通过最小化误差的平方和来寻找数据的最佳函数匹配。具体来说,OLS回归试图找到一组参数,使得模型预测值与实际观测值之间的差的平方和达到最小。
在使用OLS回归时,我们首先设定一个回归方程,这个方程定义了因变量(Y)与一个或多个自变量(X1, X2, ..., Xk)之间的关系。然后,OLS回归算法会计算出一个系数向量β,这个向量包含了各个自变量对应的最优权重,以便得到最佳的预测模型。
4.2.1 简单线性回归
我们使用lm函数进行函数拟合,我们以身高体重两个变量进行回归分析,使用内置数据集women
fit <- lm(weight ~ height, data = women)
summary(fit)
我们可视化我们的回归直线及数据点:
plot(women$height, women$weight,
xlab = '身高',
ylab = '体重',
abline(fit))
通过summary的结果,我们知道这个方程是:
体重 = -87.52 + 3.45*身高
4.2.2 多项式回归
我们可以通过添加一个二次项(X方)来提高回归准确度。
fit2 <- lm(weight ~ height + I(height^2), data = women)
summary(fit2)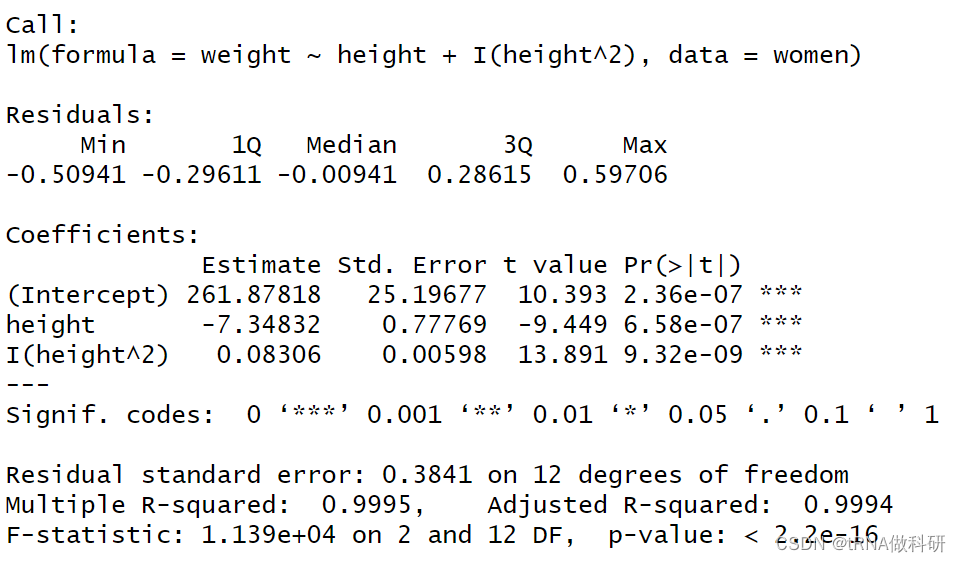
我们再进行可视化拟合:
plot(women$height, women$weight,
xlab = '身高',
ylab = '体重',
lines(women$height,fitted(fit2)) 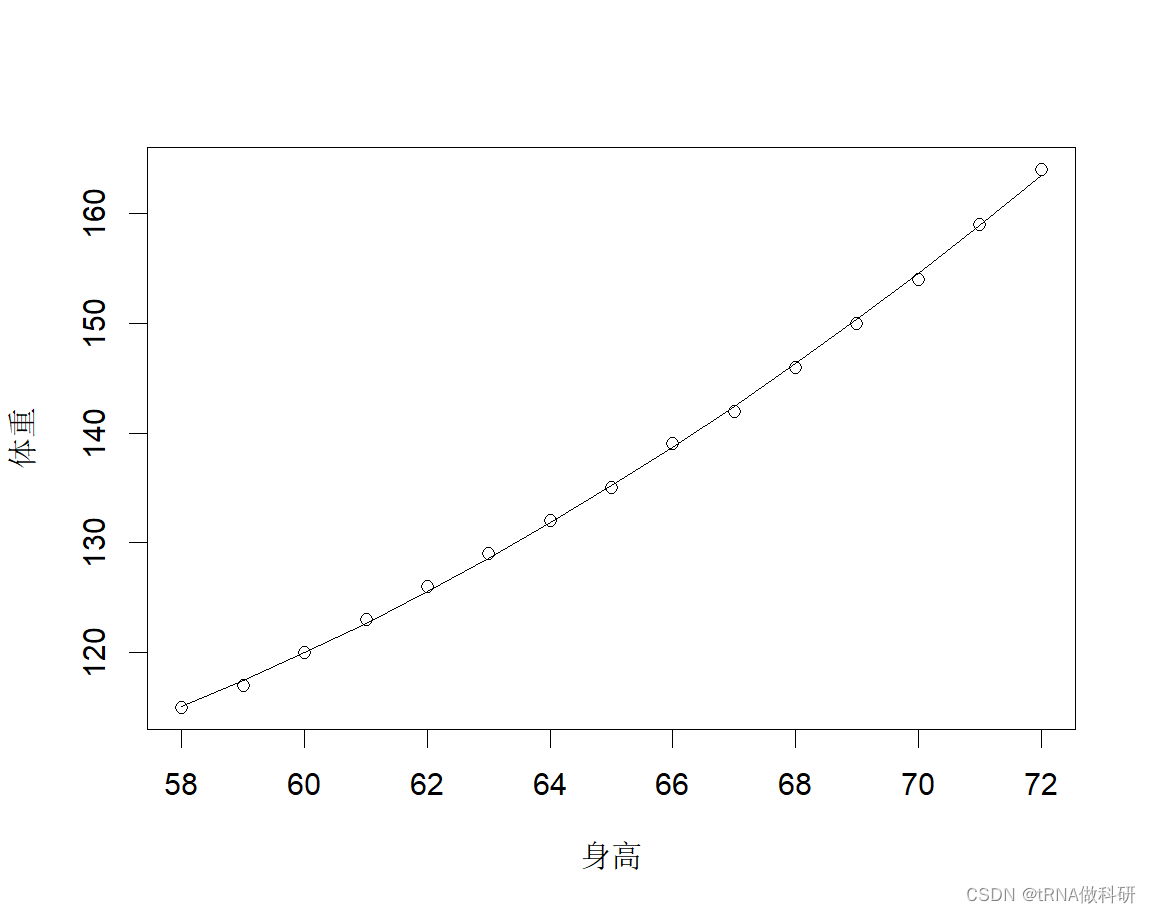
我们发现这个时候的拟合曲线比之前的要好,这时的拟合方程是:
体重 = 261.88 -7.35*身高 +0.083*身高^2
我们也可以实现n次多项式回归拟合,比如我们实现三次多项式拟合:
fit3 <- lm(weight ~ height + I(height^2) + I(height^3), data = women)
plot(women$height, women$weight,
xlab = '身高',
ylab = '体重')
lines(women$height,fitted(fit3))
4.2.3 多元线性回归
当我们遇到的问题有不止一个变量时,简单考虑x与y的关系并不能提高模型的准确度。比如我们探究一个因变量与若干自变量的关系,我们使用米国犯罪率与各个因素之间的数据进行拟合。我们选取犯罪率与人口、文盲率、平均收入及结霜天数进行多元线性回归。
一、单一变量间的相关性及进行线性拟合:
states <- as.data.frame(state.x77[,c('Murder','Population',
'Illiteracy','Income','Frost')]) #选取自变量
cor(states) #计算相关性
library(car)
scatterplotMatrix(states, spread = FALSE,
smoother.args = list(lty = 2),
main = "Scatter Plot Matrix") #绘制综合分析矩阵我们可以看到不同变量之间的相关性:

我们绘制每个变量的密度图与拟合图:

比如谋杀率随着人口及文盲率的增加而增加,这样我们会对各个自变量与因变量之间的关系有个大致的了解。
二、每个变量相互独立的多元线性回归拟合方程:
我们还是通过lm函数进行拟合:
fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data = states)
summary(fit)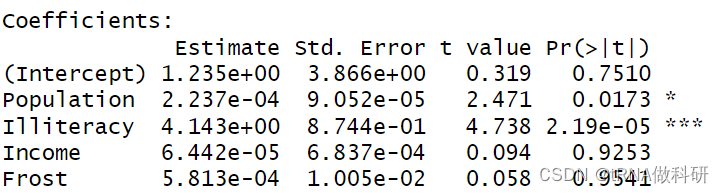
有星号的自变量是与犯罪率呈现某种关系的项,而其他项应该不呈现某种线性关系,我们通过value值来判断变量对于犯罪率的影响,比如文盲率的4是表示,在其他条件不变的情况下,文盲率每升高1%,则犯罪率升高4%。
三、变量间存在交互的多元线性回归:
当两个变量会对一个因变量产生影响,而且两个自变量间存在一定关系,我们可以进行存在交互项的回归。一般交互项通过相除建立一个新的自变量,然后给这个自变量拟合一个系数:
install.packages("MASS") # 如果没有安装MASS包,则需要先安装
library(MASS)
set.seed(123) # 设置随机种子以便结果可复现
n <- 100 # 样本大小
x1 <- rnorm(n) # 生成第一个解释变量
x2 <- rnorm(n) # 生成第二个解释变量
interaction_term <- x1 * x2 # 计算交互项
error <- rnorm(n, sd = 0.5) # 生成误差项
y <- 2 + 3*x1 - 2*x2 + 4*interaction_term + error # 生成响应变量
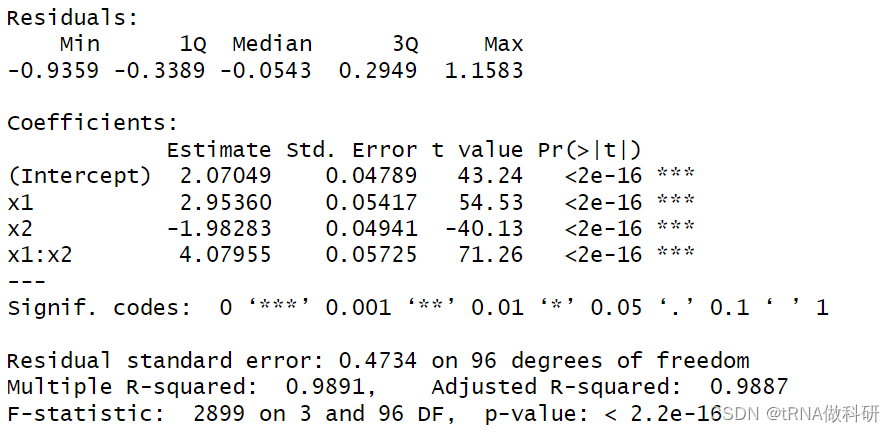
model <- lm(y ~ x1 + x2 + x1:x2) # 拟合包含交互项的模型
summary(model) # 查看模型摘要
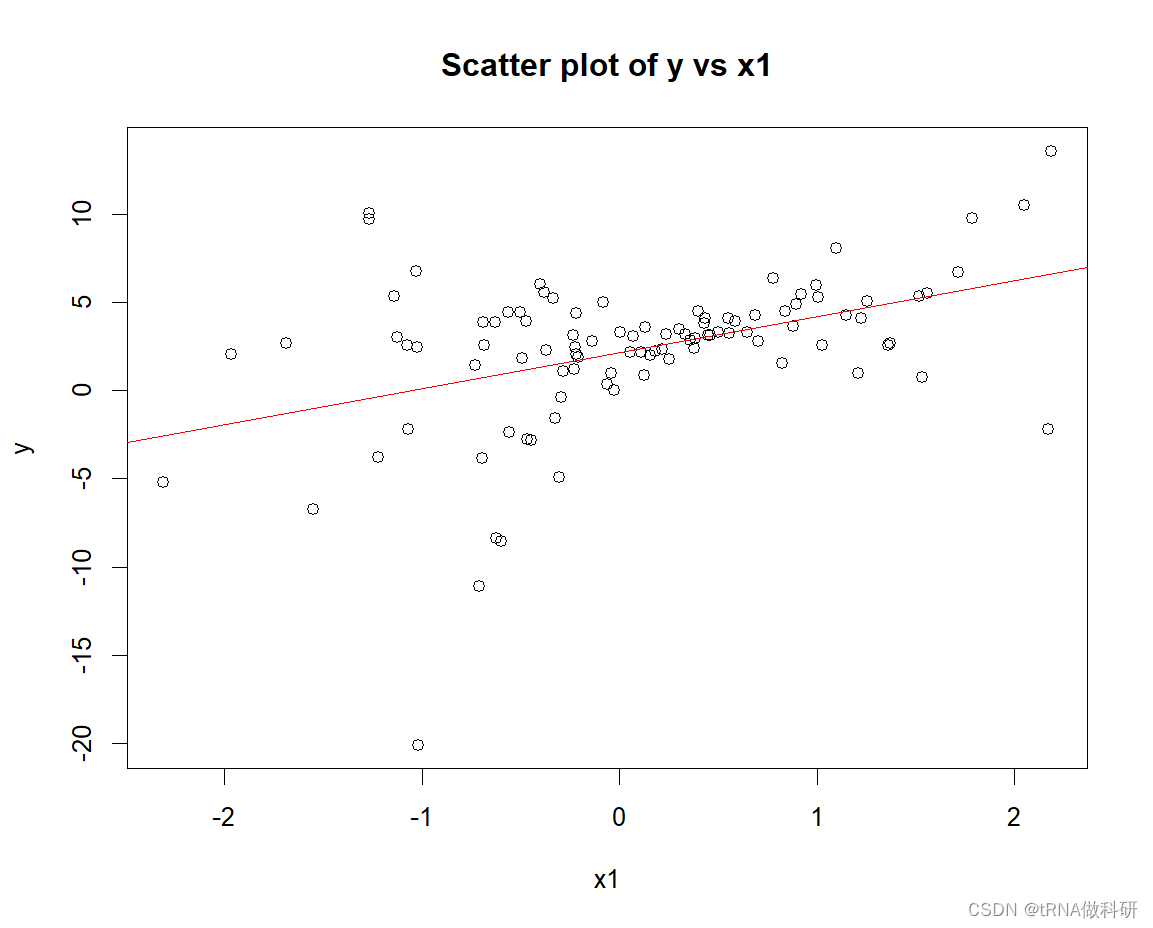
# 绘制原始数据的散点图
plot(x1, y, xlab = "x1", ylab = "y", main = "Scatter plot of y vs x1")
abline(lm(y ~ x1), col = "red") # 添加线性回归线
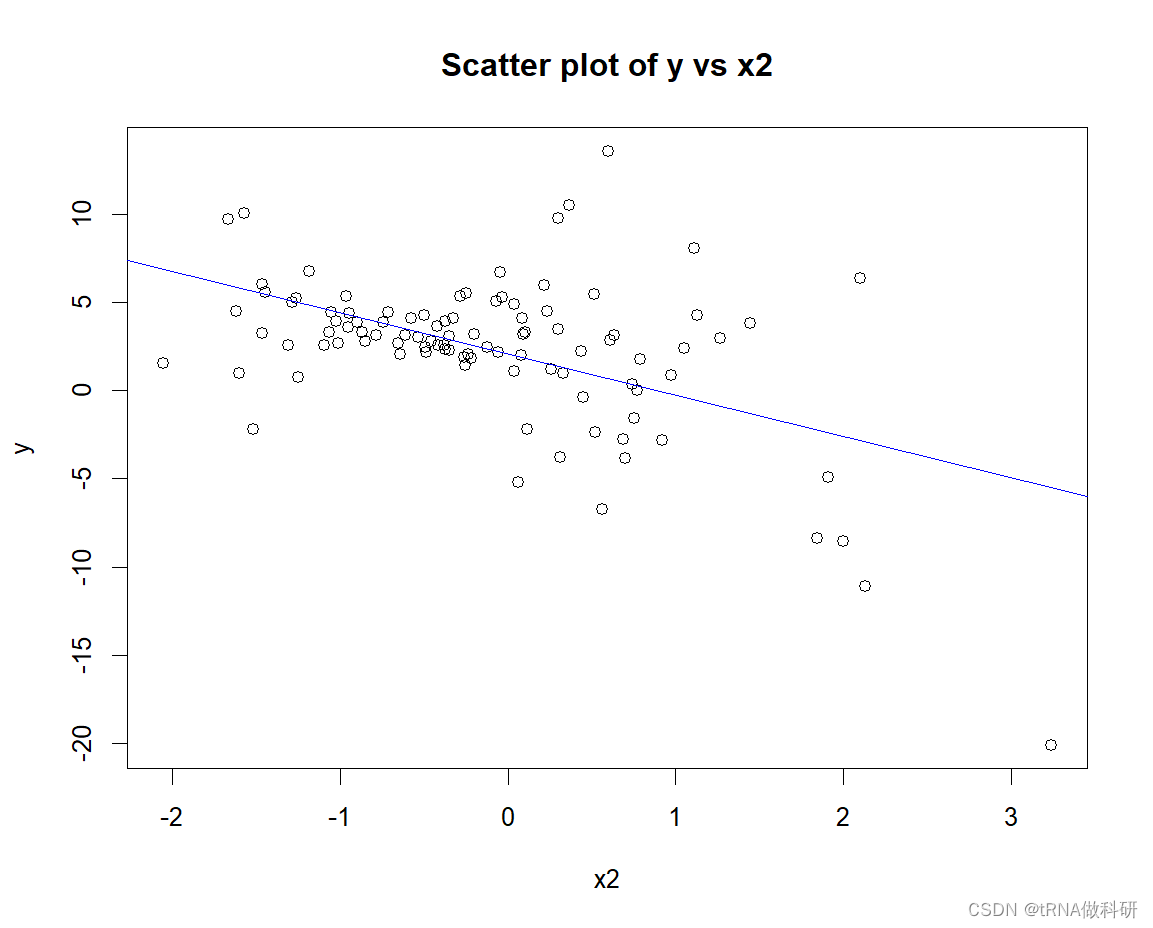
# 绘制x2与y的关系图
plot(x2, y, xlab = "x2", ylab = "y", main = "Scatter plot of y vs x2")
abline(lm(y ~ x2), col = "blue") # 添加线性回归线
# 绘制交互项与y的关系图
plot(interaction_term, y, xlab = "Interaction term", ylab = "y", main = "Scatter plot of y vs Interaction term")
abline(lm(y ~ interaction_term), col = "green") # 添加线性回归线

4.2.4 回归诊断
我们之前的拟合一般通过summary函数进行模型参数的获取,或者可视化看一下拟合,但是没有精确的指标指示拟合的好坏,因此我们学习如何进行回归诊断。
一、置信度:
我们可以查看置信区间,通过函数confint。
states <- as.data.frame(state.x77[,c('Murder','Population',
'Illiteracy','Income','Frost')]) #选取自变量
fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data = states)
confint(fit) 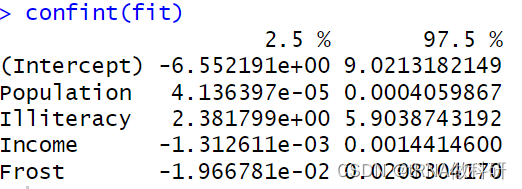
二、标准方法:
我们通过绘制判断回归正确性的四个图来进一步分析:
par(mfrow = c(2,2))
plot(fit)
我们来介绍一下这四个图的含义:
-
残差图(Residuals vs Fitted):
这个图展示了模型拟合值与残差之间的关系。理想情况下,我们希望看到残差均匀分布在零附近,没有明显的模式或趋势。如果残差随着拟合值的增加而系统性地增加或减少,这可能表明模型没有很好地捕捉到数据的某些方面,或者存在异方差性。 -
正态Q-Q图(Normal Q-Q):
正态Q-Q图用于检查残差的分布是否近似正态分布。图中会画出一条直线,表示如果数据完全来自正态分布时的期望位置。如果实际观测点紧密地围绕这条线分布,那么可以认为残差接近正态分布。偏离这条线可能意味着残差分布的非正态性,这可能会影响统计推断的准确性。 -
Scale-Location图(Scale-Location):
这个图通常用来检测异方差性,即误差项的方差是否与预测值有关。图中横轴是拟合值,纵轴是残差的绝对值或平方根。如果这些点形成一条水平线,则说明误差方差是常数;如果点的分布呈现某种模式,如上升或下降的趋势,则可能表明存在异方差性。 -
残差与杠杆图(Residuals vs Leverage):
此图结合了残差和杠杆值的信息,用于检测异常值和强影响点。杠杆值衡量了每个观测点对拟合的影响程度,高杠杆的点可能是异常值或强影响点。图中通常会画出Cook's距离的轮廓线,帮助识别那些可能对回归系数估计产生较大影响的观测点。
不过当我们想要通过删除数据来提高模型的准确度的时候,一定要记住,是模型去拟合数据,而不是数据去拟合模型。
三、改进方法:
我们使用car这个包,这个包里对于回归诊断参数的图有独立的个性化的可视化方法,绘制比刚刚plot函数更丰富更有效率的图片。
(1)QQ plot
library(car)
par(mfrow = c(1,1))
qqPlot(fit, labels=row.names(states), id.method="identify", simulate=TRUE, main="Q-Q Plot") 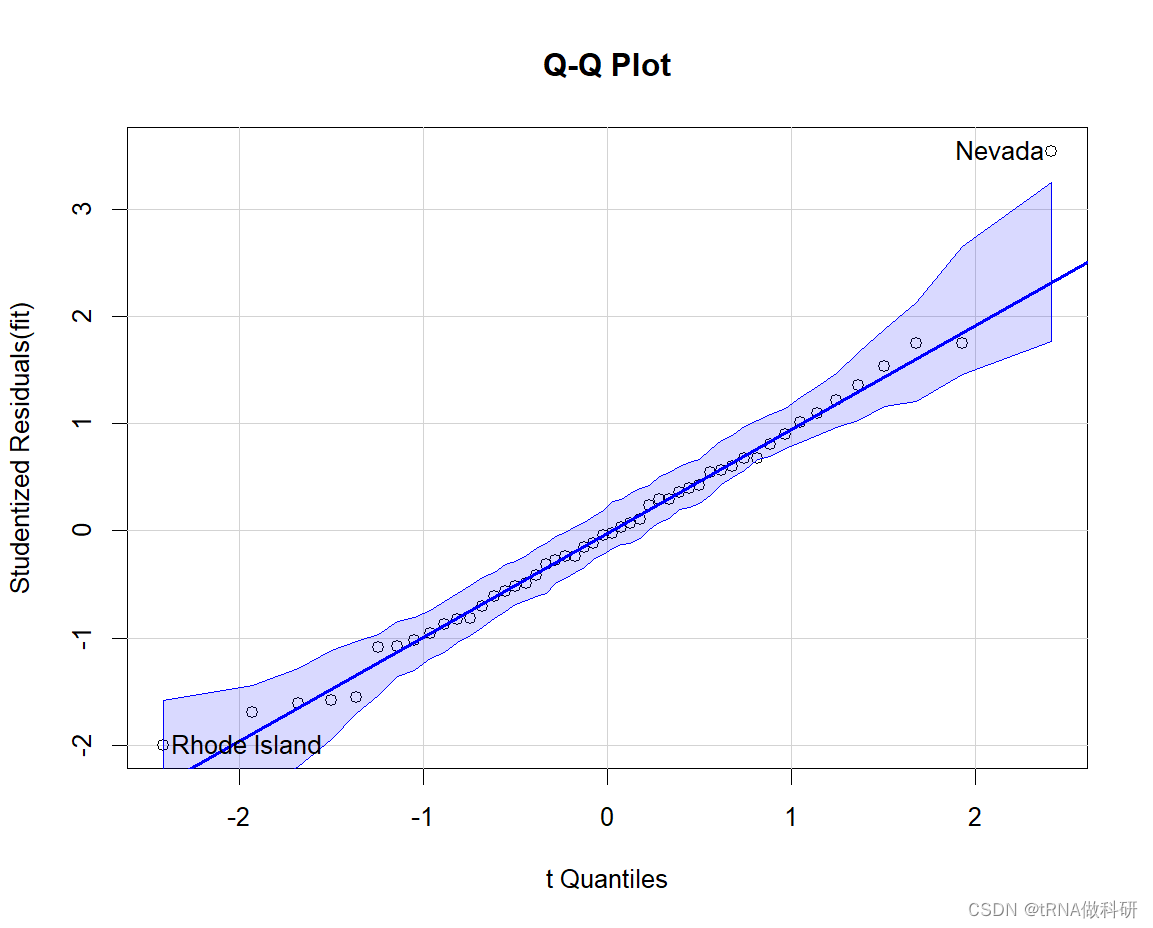
且图片中显示出两个异常的点。
(2)Stu残差图:
residplot <- function(fit, nbreaks=10) {
z <- rstudent(fit)
hist(z, breaks=nbreaks, freq=FALSE,
xlab="Studentized Residual",
main="Distribution of Errors")
rug(jitter(z), col="brown")
curve(dnorm(x, mean=mean(z), sd=sd(z)),
add=TRUE, col="blue", lwd=2)
lines(density(z)$x, density(z)$y,
col="red", lwd=2, lty=2)
legend("topright",
legend = c( "Normal Curve", "Kernel Density Curve"),
lty=1:2, col=c("blue","red"), cex=.7)
}
residplot(fit)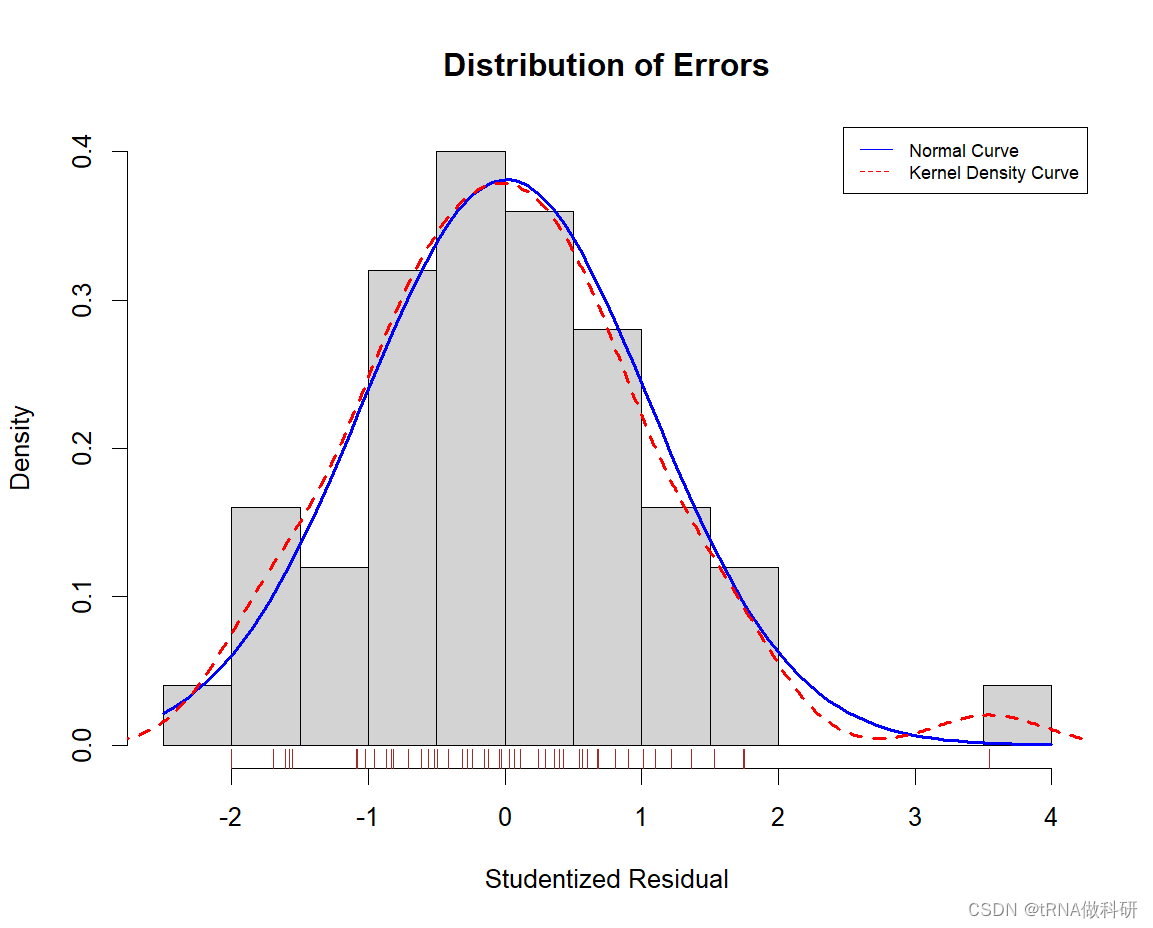
除了一个离群点外,其他点均符合正态分布。
(3)其他重要图:
我们还可以绘制部分残差图来检查非线性关系,特别是当预测变量之间可能存在交互作用时。
par(mfrow = c(2,2))
for (i in 1:ncol(states)) {
plot(states[,i], resid(fit), main = names(states)[i])
}
crPlots(fit)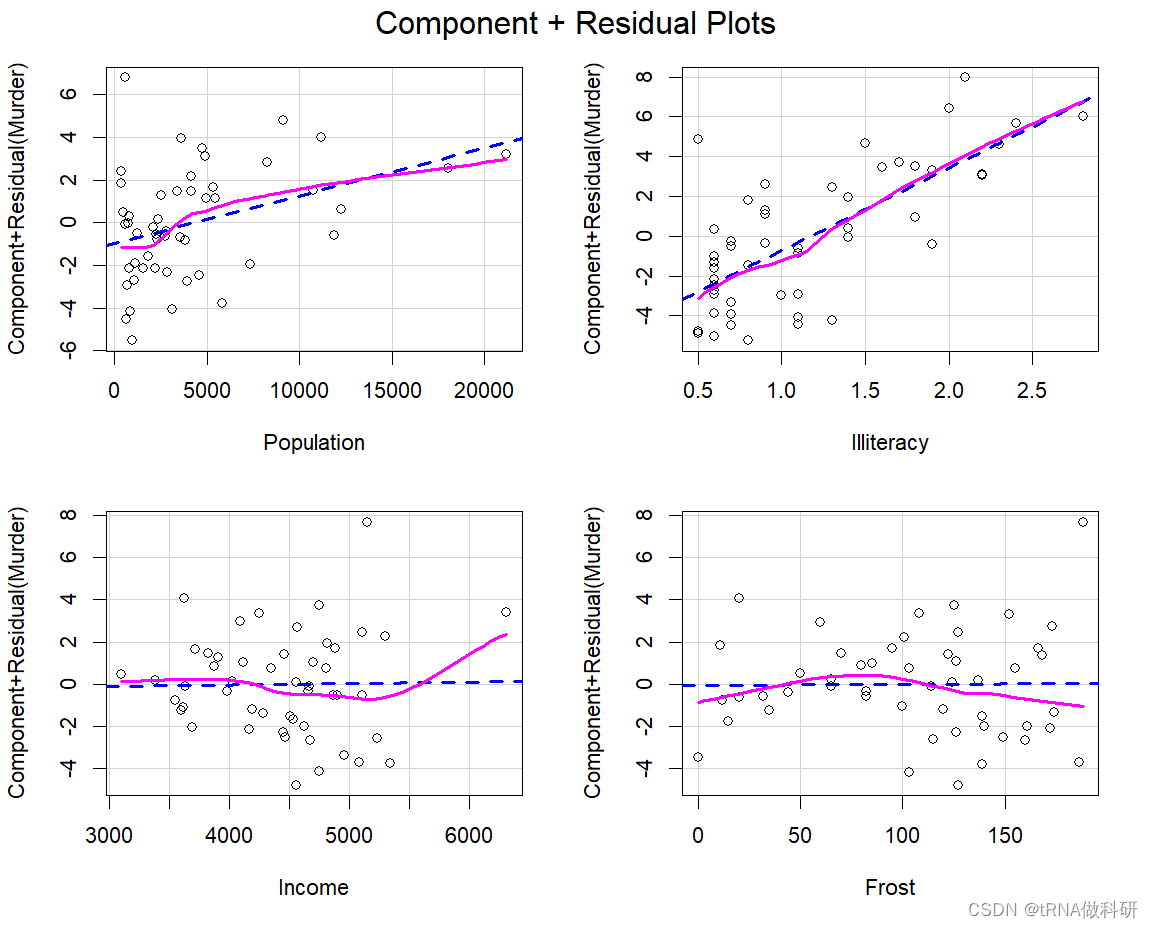
四、强影响点判断:
我们在数据中,可能因为某一个点的强大影响导致模型发生较大变化,因此我们需要鉴定这样的点。
par(mfrow = c(1,1))
cutoff <- 4/(nrow(states)-length(fit$coefficients)-2)
plot(fit, which=4, cook.levels=cutoff)
abline(h=cutoff, lty=2, col="red")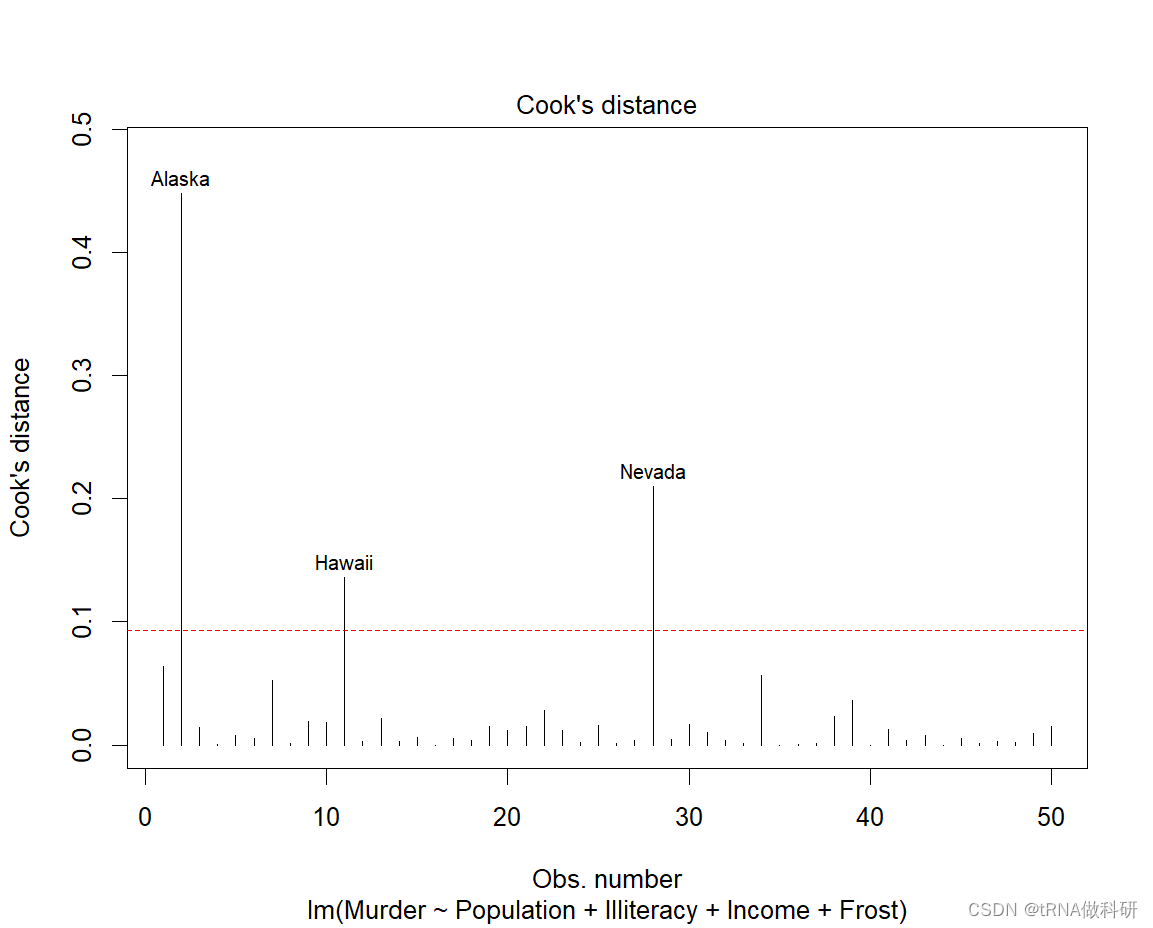
我们还可以整合离群点、杠杠值和强影响点。
influencePlot(fit)
4.2.5 回归改进
在日常工作中,我们可以通过删除异常值来帮助模型优化,但是许多时候,在数据中含有的离群点并不一定是异常值,也是模型的一部分。
一、模型比较:
我们可以使用R语言自带的anova函数进行不同模型的比较。
states <- as.data.frame(state.x77[,c('Murder','Population',
'Illiteracy','Income','Frost')]) #选取自变量
fit1 <- lm(Murder ~ Population + Illiteracy + Income + Frost, data = states)
fit2 <- lm(Murder ~ Population + Illiteracy, data = states)
anova(fit1,fit2)
我们可以得到模型中加入考虑收入和绿化率是没什么必要的。
我们还可以使用AIC函数进行不同模型的比较:
AIC(fit1,fit2)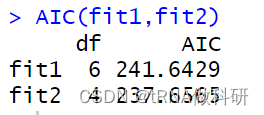
AIC值越小的模型是越好的模型。
二、变量选择:
在上述的例子中,我们已经能做出什么变量是我们所需的判断,但是在很多建模过程中,我们是不知道要选择什么样的模型的,因此模型选择是非常关键的,我们可以使用逐步回归法和全子集法。
1.逐步回归法:
我们可以对模型使用向前回归或者向后回归,向前回归就是在模型中逐个加入变量,直到模型的准确度不再发生变化,向后回归是在模型中先考虑全部的变量,然后再逐个减去变量。准确度通过AIC值来进行判断。
#向后回归
library(MASS)
fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data = states)
stepAIC(fit, direction = 'backward')
但是逐步回归法不能考虑到每一种情况,因此我们选择全子集回归。
2.全子集回归:
我们使用leaps包的regsubsets函数实现,通过我们之前学习的模型评价指标进行判定。
library(leaps)
leap <- regsubsets(Murder ~ Population + Illiteracy + Income + Frost, data = states,
nbest = 4)
plot(leap,scale = 'adjr2')
通过这个图我们能发现不同变量排列组合后,根据R2的值大小进行选择,R2大的为我们最优的选择。
4.3 深入分析
我们对于模型的泛化能力及相对重要性进行评估。
4.3.1 交叉验证
我们刚刚一直在进行方程参数的拟合,但是在面对实际问题的时候,我们会想要对数据进行预测,也就是通过我们拟合出的方程对某个预测变量进行预测。
交叉验证在我之前讲的R语言深度学习的教程中就是表示我们对于数据集拆分,一部分作为拟合模型的数据,而另外一些数据作为验证集。其实学到这里就可以学习我的R语言深度学习相关课程了。
我们可以进行n重交叉验证,也就是把数据分为n分样本,然后使用n-1份样本作为拟合,1个样本作为验证集。我们使用caret包进行交叉验证,交叉验证的方法为"cv"(cross-validation)以及折数(folds)为10。
library(caret)
# 创建一个线性模型公式
model_formula <- Murder ~ Population + Illiteracy + Income + Frost
# 设置交叉验证参数
control <- trainControl(method = "cv", number = 10)
# 使用train函数训练模型并进行交叉验证
set.seed(123) # 设置随机种子以便结果可复现
fit <- train(model_formula, data = states, method = "lm", trControl = control)
# 查看模型的汇总信息
print(fit)
结果如下:

RMSE (Root Mean Squared Error): 均方根误差是衡量模型预测值与实际观测值之间差异的一个指标。较低的RMSE值意味着模型的预测更准确。
Rsquared: R平方值衡量的是模型解释的变异量占总变异量的比例。它的值介于0和1之间,越接近1表明模型拟合得越好。
MAE (Mean Absolute Error): 平均绝对误差是另一种衡量预测误差的指标,它计算的是预测值与实际值之差的绝对值的平均值。
MPG: 如果您的数据集中有关于每加仑英里数(Miles Per Gallon)的信息,那么这部分可能展示的是该变量的预测情况。
Tuning parameter: 调整参数部分会列出模型训练过程中尝试的不同参数组合及其对应的性能指标。
4.3.2 相对重要性
之前我们对于变量进行了选择,但是有没有方法可以得到每个变量的贡献度,也就是其相对重要性。这里我们使用一个高级的方法,机器学习的随机森林算法:
library(randomForest)
# 准备数据集
states <- as.data.frame(state.x77[, c('Murder', 'Population', 'Illiteracy', 'Income', 'Frost')])
# 使用randomForest函数训练模型并获取变量重要性
set.seed(123) # 设置随机种子以确保结果的可重复性
rf_model <- randomForest(Murder ~ Population + Illiteracy + Income + Frost, data=states, ntree=500)
importance(rf_model)
# 可视化变量重要性
varImpPlot(rf_model)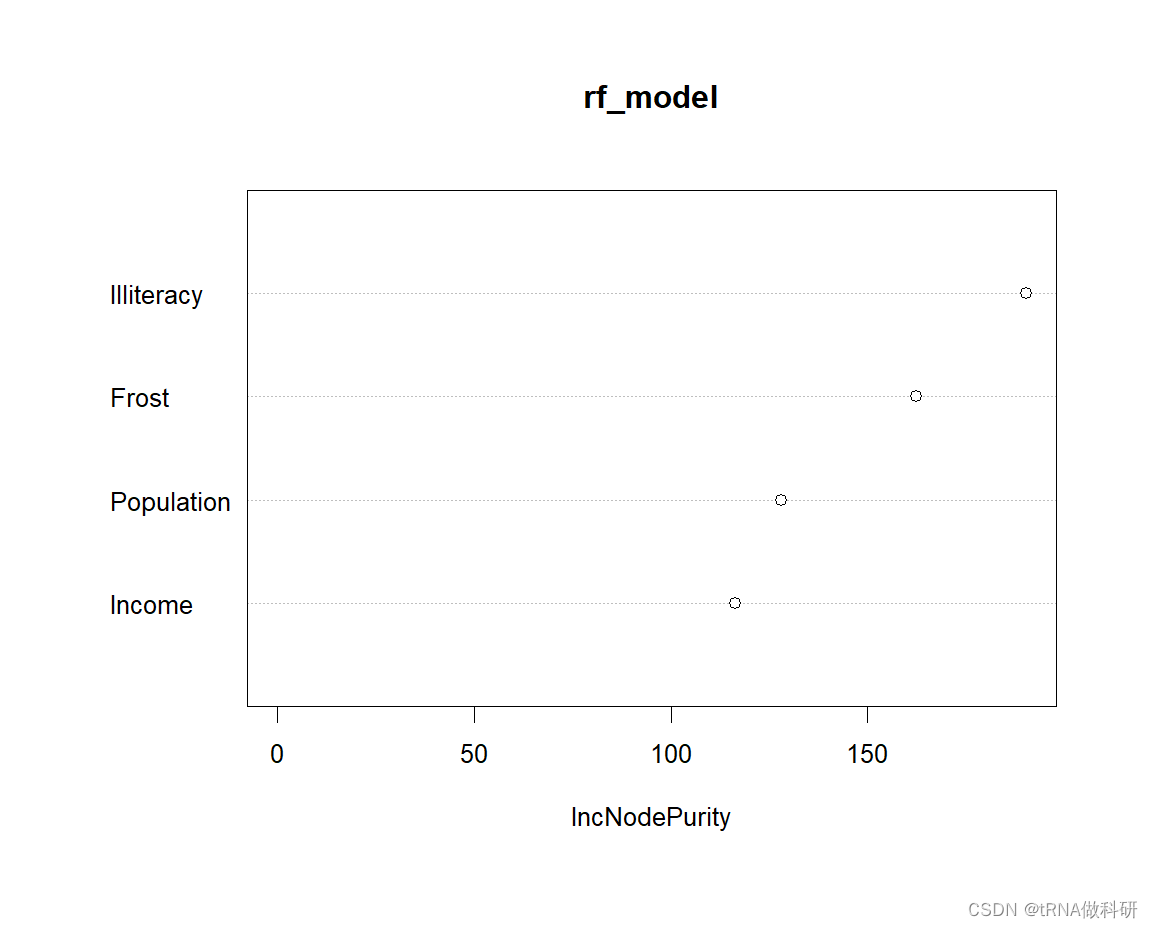
我们可以得到文盲率是最关键的因素。
4.4 小结
通过学习完本次教程,你应该已经能独立使用R语言进行数据分析及建模,并推荐可以看我之前的教程,学习R语言深度学习相关知识,建模的过程需要不断尝试,祝大家好运,有什么问题可以评论区讨论。下一个教程我们将讨论方差分析。



![[leetcode] 67. 二进制求和](https://img-blog.csdnimg.cn/direct/a36c1b59f2eb48eebd27dc7ba26116ca.png)