---

2293. 极大极小游戏

LeetCode: 2293. 极大极小游戏

$简单$

给你一个下标从 0 开始的整数数组 nums ，其长度是 2 的幂。

对 nums 执行下述算法：

1. 设 n 等于 nums 的长度，如果 n == 1 ，终止 算法过程。否则，创建 一个新的整数数组 newNums ，新数组长度为 n / 2 ，下标从 0 开始。

2. 对于满足 0 <= i < n / 2 的每个 偶数 下标 i ，将 newNums[i] 赋值 为 min(nums[2 * i], nums[2 * i + 1]) 。

3. 对于满足 0 <= i < n / 2 的每个 奇数 下标 i ，将 newNums[i] 赋值 为 max(nums[2 * i], nums[2 * i + 1]) 。

4. 用 newNums 替换 nums 。

5. 从步骤 1 开始 重复 整个过程。

执行算法后，返回 nums 中剩下的那个数字。

示例 1：

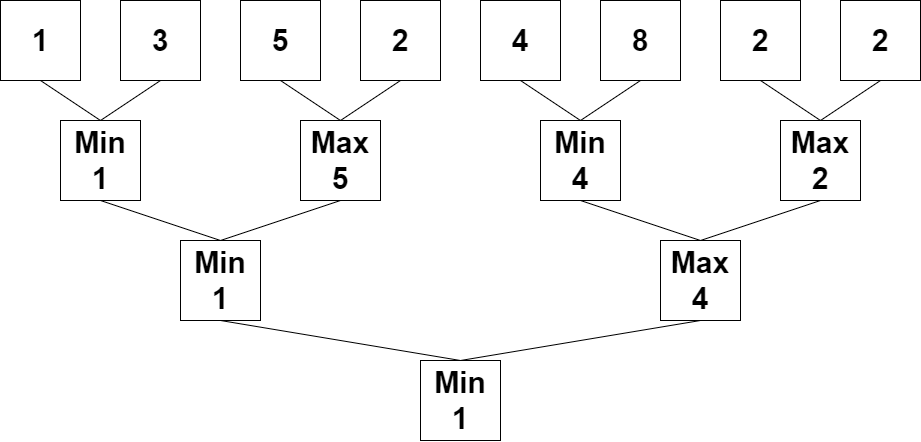
输入：nums = [1,3,5,2,4,8,2,2]
输出：1
解释：重复执行算法会得到下述数组。
第一轮：nums = [1,5,4,2]
第二轮：nums = [1,4]
第三轮：nums = [1]
1 是最后剩下的那个数字，返回 1 。

示例 2：

输入：nums = [3]
输出：3
解释：3 就是最后剩下的数字，返回 3 。

提示：

• 1 <= nums.length <= 1024
• 1 <= nums[i] <= 10^9
• nums.length 是 2 的幂

---

方法1：双指针

我们可以从 示例 1 中看到，本题的计算流程可以构成一个完全二叉树。每一层的每两个结点计算出一个值（父结点）。

我们在每处理两个数据后，可以看作这两个数据已经没有用了，同时也就意味着它们所处的 位置 也就空出来了；然后我们可以将结果存到空出来的地方。每处理 2 个数据，我们需要占用 1 个位置来存放结果，这样就空出来了一个位置，而这个位置可以存放后两个数的结果。如：

1. 处理第 0 和第 1 个数时，结果存入 0 处；
2. 处理第 2 和第 3 个数时，结果存入 1 处；
3. 处理第 4 和第 5 个数时，结果存入 2 处；
4. …

在定位两边的每次运动位置时，可以发现即将 处理 的数据总是两个两个往后遍历，结果的存放总是一个一个往后走。这就可以理解为双指针，快的指针每次走 2 步，慢的指针的步长则是 1 步。

这样一来，就得到了对于完全二叉树中某一层的遍历的思路。那么如何做到层之间的连续遍历呢？由于将每一层遍历完后，我们 有用 的数据就减少了一半，而下一层的处理便是用这些数据。我们可以限定快指针的范围。第 1 次让快指针遍历整个数组，第 2 次则让快指针遍历前一半的数组即可。

由于题目给出条件：数组 nums 的长度为 2 的整数次幂，那就表明这个长度就一定能被 2 整除。快指针每次走2步也就不会产生 少处理数据 或者 越界 的错误。

#include <vector>
#include <utility>
using namespace std;

class Solution
{
public:
    int minMaxGame(vector<int> &nums)
    {
        for (int count = nums.size(); count != 1; count >>= 1)
        {
            for (int fast = 0, slow = 0; fast <= count - 1; fast += 2, ++slow)
            {
                if ((slow & 1) == 0)
                    nums[slow] = std::min(nums[fast], nums[fast + 1]);
                else
                    nums[slow] = std::max(nums[fast], nums[fast + 1]);
            }
        }

        return nums[0];
    }
};

复杂度分析

• 时间复杂度：$O(n)$。其中，n 为数组 nums 的长度。
  • 第一次循环的时间复杂度为 $O(n)$ ，之后每次循环的时间复杂度依次减半。因此时间复杂度最终为：

$$O(n)+O(\frac{n}{2})+O(\frac{n}{4})+...=O(n\times \underset{k\to 0^{+}}{\lim }\frac{1\times (1-(\frac{1}{2}{)}^k)}{1-\frac{1}{2}})=O(n\times \frac{1}{1-\frac{1}{2}})=O(n)$$

• 空间复杂度：$O(1)$。我们使用 nums 数组原地处理数据，没有用到额外的、大小与输入数据有关的变量，因此常用常数的额外空间。

参考结果

Accepted
96/96 cases passed (4 ms)
Your runtime beats 94.42 % of cpp submissions
Your memory usage beats 70.70 % of cpp submissions (9.5 MB)