目录
- 神经网络第一层(隐藏层)计算过程
- 1.输入向量
- 2.神经元的计算
- 2.标识不同神经元
- 3.层输出(激活)向量
- 4.神经网络分层
- 5.标识不同层
- 神经网络第二层(输出层)计算过程
- 1.输入向量
- 2.层输出(激活)
- 3.标识不同神经元和层数
- 神经网络的最终预测
- 总结
神经网络第一层(隐藏层)计算过程
1.输入向量
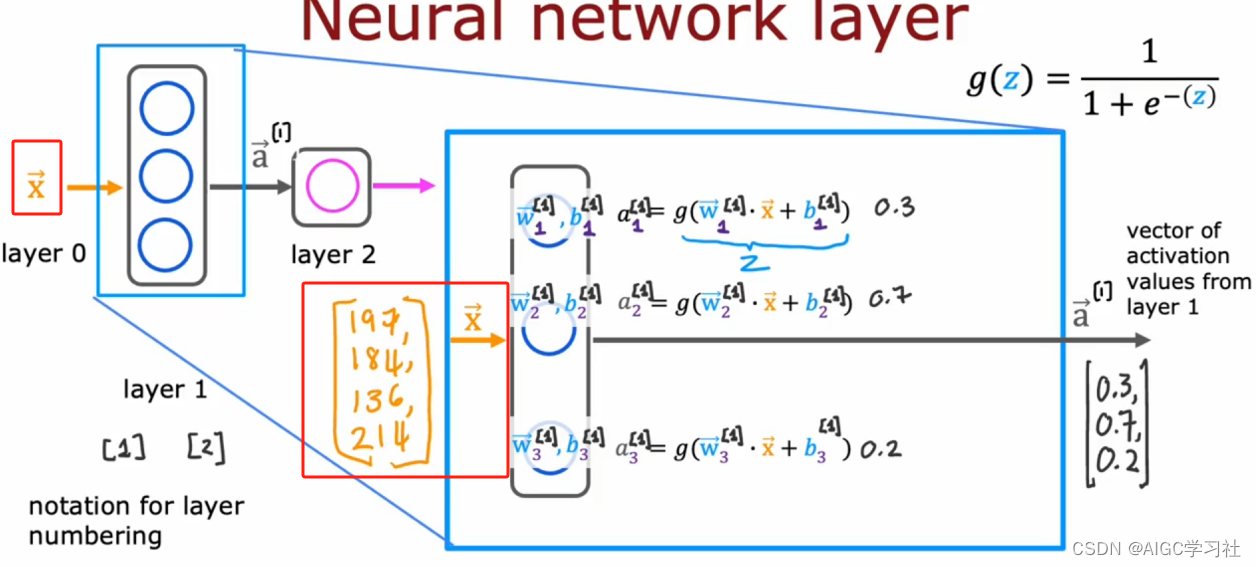
输入向量x,x包含四个数字,它作为第一层的输入特征。
2.神经元的计算
每个神经元都是一个逻辑回归模型,因此都具备自己的w,b参数,使用向量x计算g(z)函数,激活项表示概率,例如有0.3或0.7的概率想要T恤。
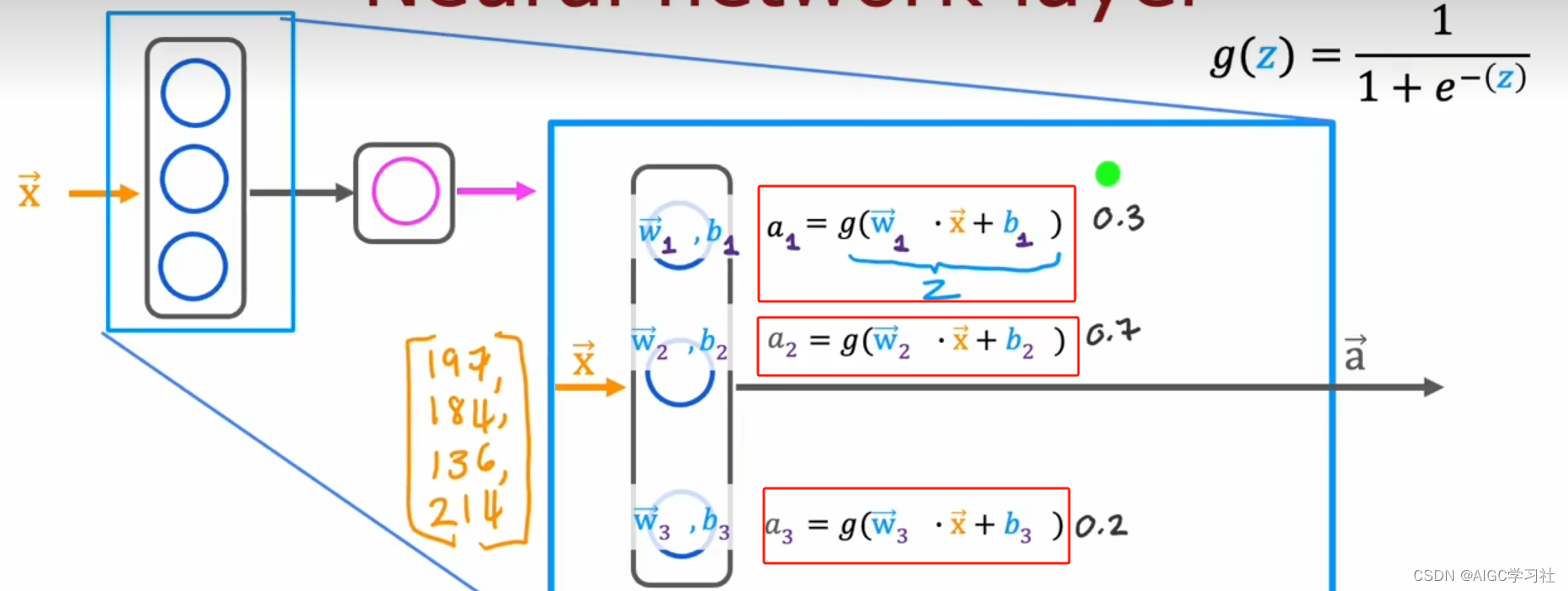
2.标识不同神经元
下标数字,表示该参数属于一层里哪个神经元。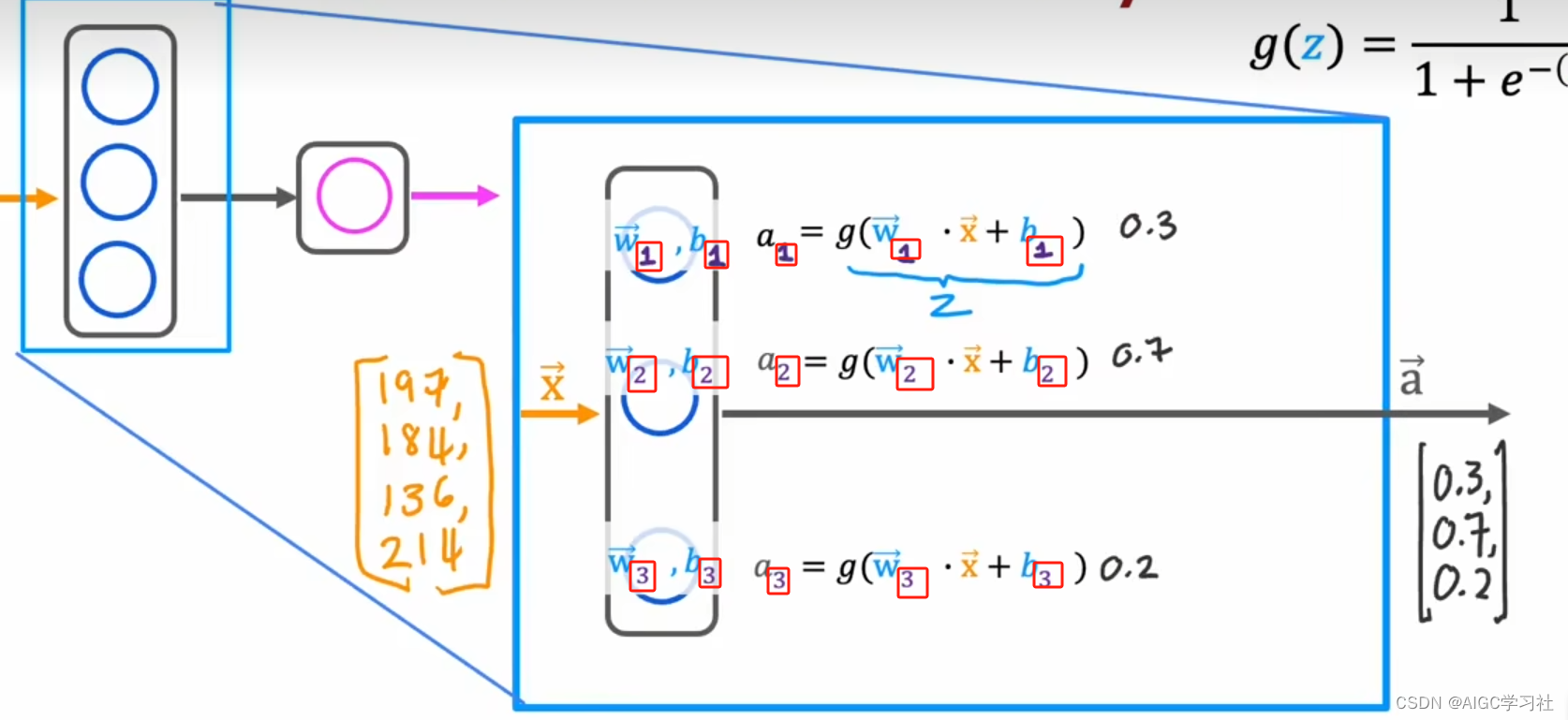
3.层输出(激活)向量
第一层的3个激活值,合并成激活向量a。

4.神经网络分层
此示例中,输入层为0层,隐藏层为1层,输出层为2层。
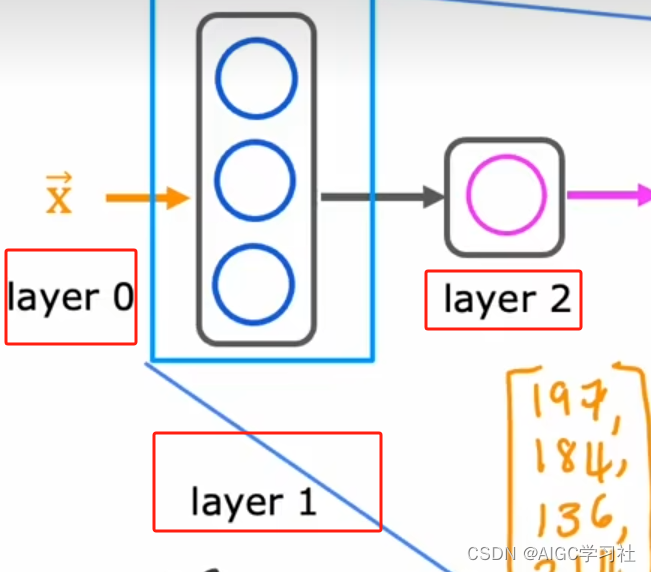
5.标识不同层
上标使用中括号+数字来区分不同层,例如隐藏层的参数上标标注1,隐藏层的激活向量a上标标注1。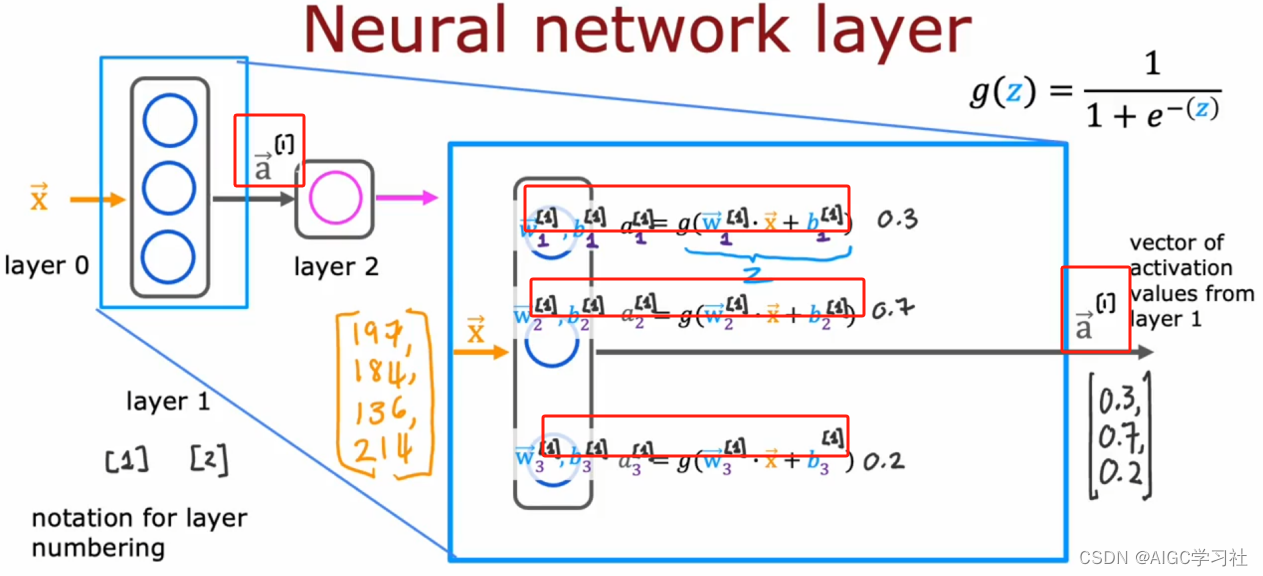
神经网络第二层(输出层)计算过程
1.输入向量
第1层的激活项为第2层的输入特征,因此神经元计算需要的输入特征x,就是激活向量a,激活向量a表示第1层的输出结果,因此右上角标注1。
2.层输出(激活)
第2层只有1个神经元,因此激活值只有一个0.84,a的右上角标注2,表示第2层的激活值。
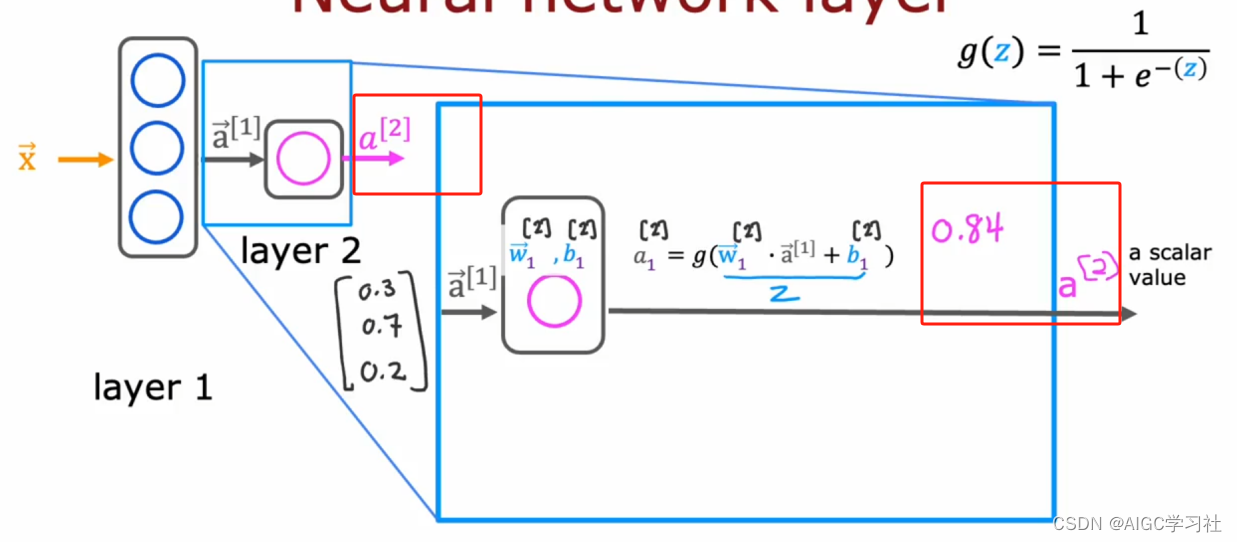
3.标识不同神经元和层数
右上角的2,表示这些参数是第2层。有下角的1,表示这些参数属于这层的第1个神经元。
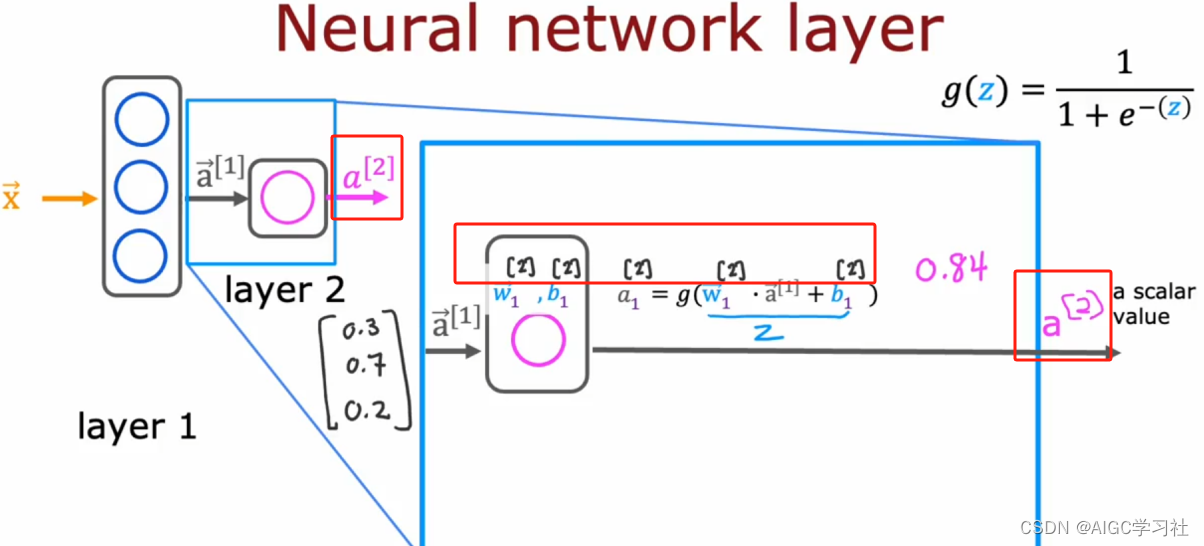
神经网络的最终预测
最终预测结果为0.84,它代表产品畅销的概率。同时可以将输出转换为二分类,使用阈值来将结果设定为是否畅销,如果大于等于0.5,则y=1表示畅销,如果小于0.5,则y=0表示不畅销。
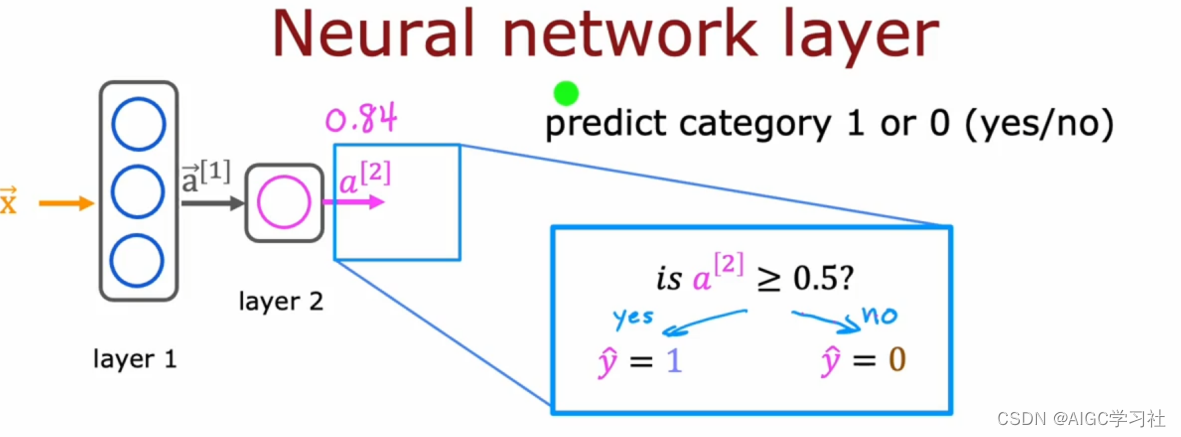
总结
神经网络会存在很多层,每一层也存在很多神经元。每一个神经元都可以作为一个逻辑回归模型,因此每个神经元都有自己的参数w,b。区别不同的神经元参数,每个参数的下标标记数字。为了区别不同的层,每个参数的上标标记数字。每一层的激活项都是下一个层的输入特征,因此每一层的输入,上标标记上一层的层数,同时每一层的激活项,上标标记本层的层数。