目录
1.二叉搜索树的概念
2.二叉搜索树的实现
2.1总体代码预览
2.2各个函数实现原理
链表结构体
二叉搜索树的成员变量
二叉搜索树的插入
二叉搜索树的查找
二叉搜索树的遍历
二叉搜索树的删除
1.二叉搜索树的概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
1.若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
2.若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
3.它的左右子树也分别为二叉搜索树
2.二叉搜索树的实现
由上面的定义,我们知道二叉搜索树的左孩子是小于父亲的,而右孩子是大于父亲的。由这个规律我们就可以实现一下这个二叉搜索树。
2.1总体代码预览
template<class k> struct BSTreeNode { BSTreeNode<k>* _left; BSTreeNode<k>* _right; k _key; BSTreeNode(const k& key) :_left(nullptr) ,_right(nullptr) ,_key(key) {} }; template<class K> class BST { typedef BSTreeNode<K> Node; public: bool Insert(const K& key) { if (_root == nullptr) { _root = new Node(key); return true; } Node* parent = nullptr; Node* cur = _root; while (cur) { if (key > cur->_key) { parent = cur; cur = cur->_right; } else if (key < cur->_key) { parent = cur; cur = cur->_left; } else { return false; } } cur = new Node(key); if (key < parent->_key) { parent->_left = cur; } else { parent->_right = cur; } return true; } bool Find(const K& key) { Node* cur = _root; while (cur) { if (key > cur->_key) { cur = cur->_right; } else if (key < cur->_key) { cur = cur->_left; } else { return true; } } return false; } bool Erase(const K& key) { Node* parent = nullptr; Node* cur = _root; while (cur) { if (key > cur->_key) { parent = cur; cur = cur->_right; } else if (key < cur->_key) { parent = cur; cur = cur->_left; } else { //删除 if (cur->_left == nullptr) { if (cur == _root) { _root = cur->_right; } else { if (parent->_left == cur) { parent->_left = cur->_right; } else if (parent->_right == cur) { parent->_right = cur->_right; } } delete cur; } else if (cur->_right == nullptr) { if (cur == _root) { _root = cur->_left; } else { if (parent->_left == cur) { parent->_left = cur->_left; } else if (parent->_right == cur) { parent->_right = cur->_left; } } delete cur; } //cur左右都不为空 else { Node* rightminparent = cur; Node* rightmin = cur->_right; while (rightmin->_left) { rightminparent = rightmin; rightmin = rightmin->_left; } swap(rightmin->_key, cur->_key); if(rightminparent->_left== rightmin) rightminparent->_left = rightmin->_right; else rightminparent->_right = rightmin->_right; delete rightmin; } return true; } } return false; } void InOrder() { _InOrder(_root); } private: void _InOrder(Node* root) { if (root == nullptr) { return; } _InOrder(root->_left); cout << root->_key << endl; _InOrder(root->_right); } Node* _root=nullptr; };2.2各个函数实现原理
链表结构体
template<class k> struct BSTreeNode { BSTreeNode<k>* _left; BSTreeNode<k>* _right; k _key; BSTreeNode(const k& key) :_left(nullptr) ,_right(nullptr) ,_key(key) {} };既然是我们的二叉树,那么链表的部分肯定是不能少的吧,这个链表里面,我们来定义左右孩子的指针,还有用来进行标识的key值,接下来就可以写一下它的构造函数,这个节点一开始肯定是没有左右孩子的,所以我们给它们赋上空指针,而key就是我们传的key。
二叉搜索树的成员变量
Node* _root=nullptr;二叉搜索树的成员变量就很简单了,我们直接定义一个结构体指针的变量的就可以了。Node类型是我们重命名链表名后的名字。
二叉搜索树的插入
bool Insert(const K& key) { if (_root == nullptr) { _root = new Node(key); return true; } Node* parent = nullptr; Node* cur = _root; while (cur) { if (key > cur->_key) { parent = cur; cur = cur->_right; } else if (key < cur->_key) { parent = cur; cur = cur->_left; } else { return false; } } cur = new Node(key); if (key < parent->_key) { parent->_left = cur; } else { parent->_right = cur; } return true; }插入的逻辑其实非常简单,如果这棵树是一棵空树,那么我们直接创个根节点就可以了,不需要后续的操作,倘若不是空树,那我们就进行接下来的操作,我们先定义一个父亲节点parent和当前节点cur,然后按照我们的性质,key比cur中的大我们就往右,小的话我们就往左走,如果这个key在树中存在,我们就放回false,因为set是有去重功能的,就是说一棵树里不能存在两个一样的值。找到了适合的位置我们就出循环,然后开始创建节点,进行连接就可以了。
二叉搜索树的查找
bool Find(const K& key) { Node* cur = _root; while (cur) { if (key > cur->_key) { cur = cur->_right; } else if (key < cur->_key) { cur = cur->_left; } else { return true; } } return false; }查找的功能就更简单了,我们只需要按照性质,左边比根小右边比根大就可以了。
二叉搜索树的遍历
void _InOrder(Node* root) { if (root == nullptr) { return; } _InOrder(root->_left); cout << root->_key << endl; _InOrder(root->_right); }我们的二叉搜索树按照中序遍历是刚好是有序的,这个是我们二叉搜索树的意义之一,所以我们这里也是实现中序遍历。
中序遍历的思想就简单的多了,使用递归对它的各个节点进行遍历就可以了。
但是我们调用中序遍历肯定不想别人传个参数,所以我们再进行封装就可以了。
二叉搜索树的删除
bool Erase(const K& key) { Node* parent = nullptr; Node* cur = _root; while (cur) { if (key > cur->_key) { parent = cur; cur = cur->_right; } else if (key < cur->_key) { parent = cur; cur = cur->_left; } else { //删除 if (cur->_left == nullptr) { if (cur == _root) { _root = cur->_right; } else { if (parent->_left == cur) { parent->_left = cur->_right; } else if (parent->_right == cur) { parent->_right = cur->_right; } } delete cur; } else if (cur->_right == nullptr) { if (cur == _root) { _root = cur->_left; } else { if (parent->_left == cur) { parent->_left = cur->_left; } else if (parent->_right == cur) { parent->_right = cur->_left; } } delete cur; } //cur左右都不为空 else { Node* rightminparent = cur; Node* rightmin = cur->_right; while (rightmin->_left) { rightminparent = rightmin; rightmin = rightmin->_left; } swap(rightmin->_key, cur->_key); if(rightminparent->_left== rightmin) rightminparent->_left = rightmin->_right; else rightminparent->_right = rightmin->_right; delete rightmin; } return true; } } return false; }二叉搜索树的删除才是我们的真正难点
我们最开始的操作还是一样的,我们要找那个被删除的节点,找到后就开始我们的操作了。我们有三种大情况:
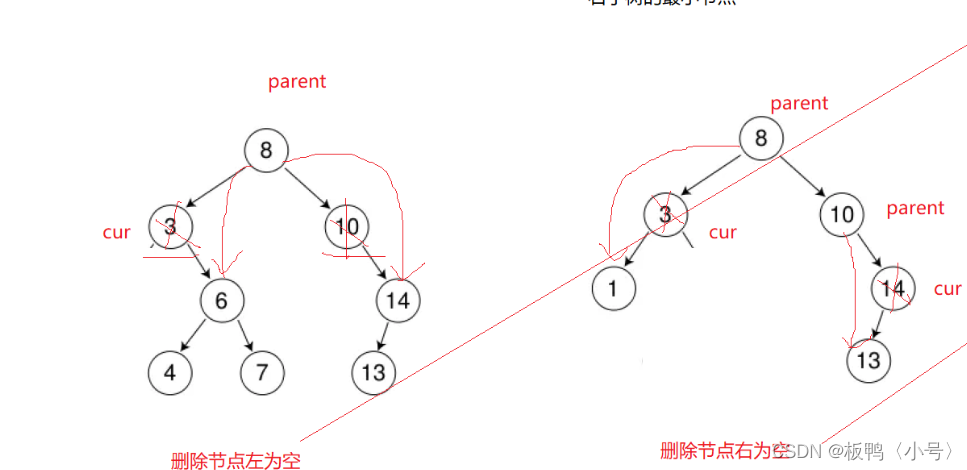
第一种是要删除的节点左孩子为空的时候:
如图所示,我们的cur只有一边是有值的,这个时候我们先判断这个cur是父亲的左孩子还是右孩子,然后再把链表指向修改就行了,但是不要忘记了,我们的cur有可能是根节点,这个时候我们的父亲节点是空,这个时候是没法去给parent修改指向的,所以我们要单独的写一个判断。
第二种自然就是右孩子为空了,思路跟左孩子是一模一样的。
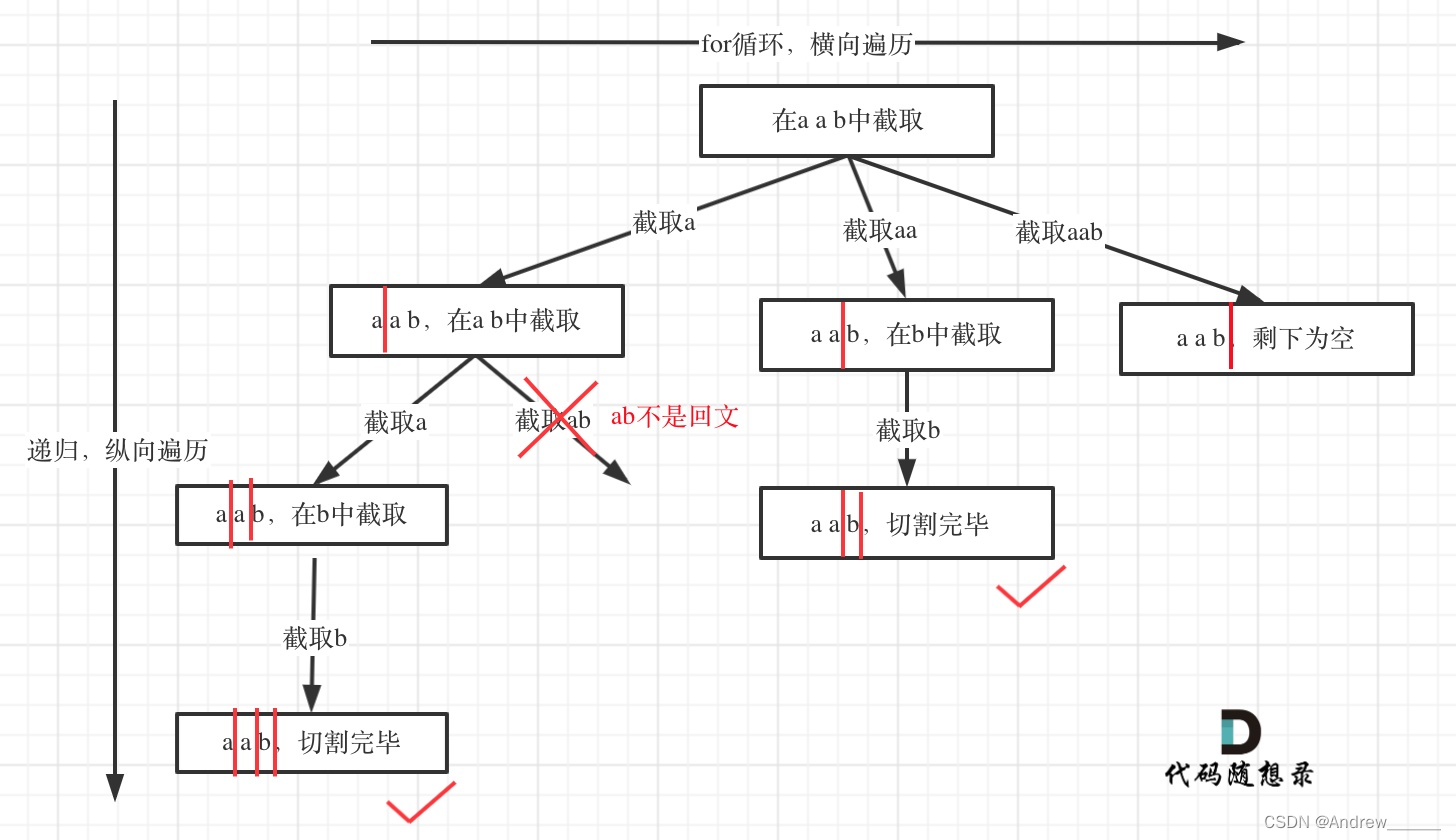
第三种就是我们的cur的左右孩子都不为空,这里的做法右两种,第一种是找cur的左子树的最大值,替换cur,然后再把cur给删除,第二种是找右子树的最小值,然后进行同样的操作,这两种做法都可以使其保持二叉搜索树该有的性质。这里我们选择第二种。
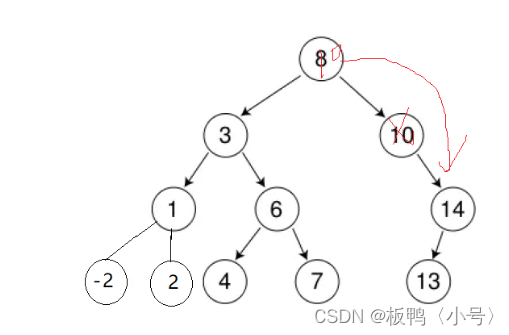
可以看到外面用循环来找到右子树的最小值,找到后交换值,我们没有直接让rightminparent的左节点直接接向rightmin的右子树是因为可能有这种情况
假如我们删的是8,这个时候右孩子是没有左节点的,这个时候我们就不可能rightminparent的左节点接向rightmin的右子树,所以我们进行了这个分类讨论,这个细节也是很难想到的。
至此我们的二叉搜索树的实现原理就讲完了,感谢大家的收看!
C++实现二叉搜索树(模型)
news2026/2/13 18:14:31
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1648543.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
python 使用 MQTT
目录结构 1、py代码
offRelay12-yixing.py
# _*_ coding: utf-8 _*_
# 须用到第三方库:paho-mqtt
# 安装命令 python3 -m pip install paho-mqttimport time
import json
import paho.mqtt.client as mqtt# 函数:关闭所有房间的12路继电器模块上指定的…
BIGRU、CNN-BIGRU、CNN-BIGRU-ATTENTION、TCN-BIGRU、TCN-BIGRU-ATTENTION合集
(BIGRU、CNN-BIGRU、CNN-BIGRU-ATTENTION、TCN-BIGRU、TCN-BIGRU-ATTENTION)时,我们可以从它们的基本结构、工作原理、应用场景以及优缺点等方面进行详细介绍和分析。 BIGRU、CNN-BIGRU、CNN-BIGRU-ATTENTION、TCN-BIGRU等(matlab…
NXP i.MX8系列平台开发讲解 - 1.1 导读前言
专栏文章目录传送门:返回专栏目录 文章目录
目录
1. 本专辑介绍
2. 学习本专辑作用
3.关于作者 1. 本专辑介绍
本专辑将会介绍Linux 驱动开发,Android BSP 驱动涉及HAL层调试,适用于嵌入式软件开发人员,和有兴趣向该方向发展…
jenkins目录下的vue3项目——pnpm install后运行报错——奇葩问题解决
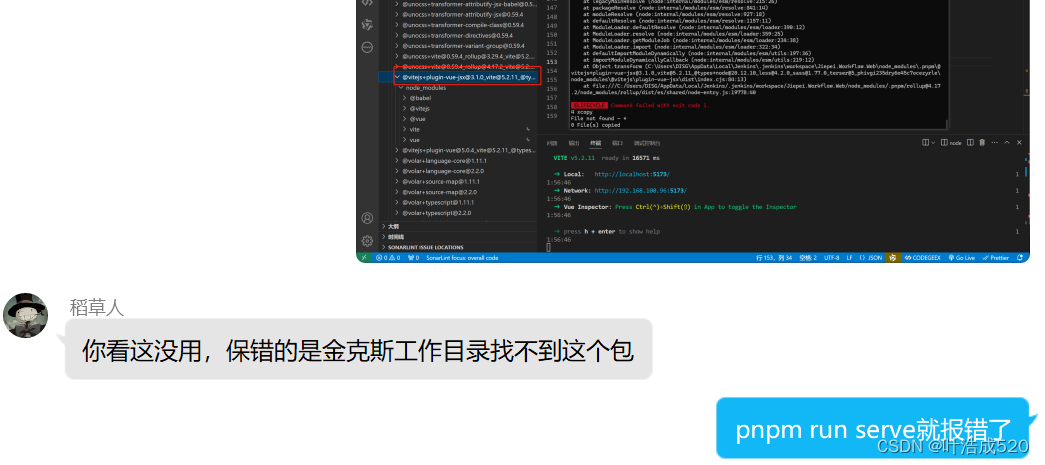
昨天到今天,同事那边遇到一个问题,就是关于vue3vite的项目,在执行了自动打包后,运行代码会提示报错的问题。
报错信息如下: 具体错误信息如下: ERROR 11:28:14 [vite] Pre-transform error: Cannot find …
零基础代码随想录【Day27】|| 39. 组合总和,40.组合总和II, 131.分割回文串
目录
DAY27
39. 组合总和
解题思路&代码
40.组合总和II
解题思路&代码
131.分割回文串
解题思路&代码 DAY27
39. 组合总和
力扣题目链接(opens new window)
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有…
【xxl-job | 第三篇】SpringBoot整合xxl-job
文章目录 3.SpringBoot整合xxl-job3.1定时任务服务配置3.1.1导入maven依赖3.1.2yml配置3.1.3XxlJobConfig配置类3.1.4定时任务类 3.2xxl-job配置3.2.1新增执行器3.2.2新增任务3.2.3执行任务3.2.4查看日志3.2.5查看任务后台日志 3.3小结 3.SpringBoot整合xxl-job
3.1定时任务服…
计划订单转采购申请的增强点和可以增强的内容
MD15 MD14 计划订单转采购申请,涉及的增强点和增强内容 对于外协的采购申请,有时候需要对组件的内容做一些特殊的处理,但是处理组件清单的增强ME_COMPONENTS_UPDATE的增强点(这个增强点对于手工创建的外协PR、外协PO,外协pr转外协…
【硬核科普】一文读懂生成对抗网络GAN
0. 前言 按照国际惯例,首先声明:本文只是我自己学习的理解,虽然参考了他人的宝贵见解及成果,但是内容可能存在不准确的地方。如果发现文中错误,希望批评指正,共同进步。 本文基于Ian在2014年发表在NIPS的论…
2024年口碑最好的游泳耳机有哪些,这四款游泳耳机值得相信!
随着科技的不断进步和人们对健康生活的追求,游泳已经成为许多人健身和放松的首选运动之一。然而,想要在游泳时享受音乐的乐趣却一直是一个挑战。传统的耳机往往无法抵御水的侵蚀,导致音质下降或者设备损坏。因此,游泳耳机的问世成…
ubuntu20部署3d高斯
3d高斯的链接:https://github.com/graphdeco-inria/gaussian-splatting
系统环境
ubuntu20的系统环境,打算只运行训练的代码,而不去进行麻烦的可视化,可视化直接在windows上用他们预编译好的exe去可视化。(因为看的很…
使用Beego创建API项目并自动化文档
最近需要使用Go写一个Web API项目,可以使用Beego与Gin来写此类项目,还是非常方便的,这里就介绍一下使用Beego来创建的Web API项目并自动化文档的方法。
使用Gin创建API项目并自动化文档参见:使用Gin编写Web API项目并自动化文档 …
Android(一)
坏境
java版本 下载 Android Studio 和应用工具 - Android 开发者 | Android Developers
进入安卓官网下载 勾选协议 next 如果本地有设置文件,选择Config or installation folder
如果本地没有设置文件,选择Do not import settings 同意两个协议 耐…
idea提示 CreateProcess error=206, 文件名或扩展名太长有哪些具体的解决方法
背景: 项目启动后提示CreateProcess error206,通常我本地是将shorten command line改成如下就可以解决,但是今天遇到一个,无论这里怎么设置都是启动提示扩展名太长,经过一番处理问题终于解决,特此记录一下。…
Leetcode—1235. 规划兼职工作【困难】(upper_bound、自定义排序规则)
2024每日刷题(125)
Leetcode—1235. 规划兼职工作 算法思想 实现代码
class Solution {
public:int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {int n startTime.size();vec…
RabbitMQ的介绍和使用
1.同步通讯和异步通讯 举个例子,同步通讯就像是在打电话,因此它时效性较强,可以立即得到结果,但如果你正在和一个MM打电话,其他MM找你的话,你们之间是不能进行消息的传递和响应的 异步通讯就像是微信&#…
基于GEE遥感影像处理和长时序土地分类以及生物量估算分析
简介 Google Earth Engine云平台是目前全球范围内测绘领域内使用最为广泛的遥感云计算平台,其凭借强大的数据存储和云计算能力,极大了提高了全球科研工作者的科研产出,每年借助GEE平台发布的各类期刊论文超1000篇,在海量遥感数据的…
鉴源实验室丨汽车入侵检测系统介绍及测试
作者 | 张诏景 上海控安可信软件创新研究院工控网络安全组
来源 | 鉴源实验室
社群 | 添加微信号“TICPShanghai”加入“上海控安51fusa安全社区” 01
入侵检测系统背景
智能网联汽车不再是一个孤立的嵌入式系统了,信息安全问题越来越被重视。国内外发布了多项标…
Jmeter 命令行压测 生成 HTML 测试报告,你真的会?
通常 Jmeter 的 GUI 模式仅用于调试,在实际的压测项目中,为了让压测机有更好的性能,多用 Jmeter 命令行来进行压测。
同时,JMeter 也支持生成 HTML 测试报告, 以便从测试计划中获得图表和统计信息。 以上定义的文件路…
无人售货机是否是下个风口?
当前,众多大中城市正逐步转变为无人零售的新兴试验场,其广阔的发展前景与潜在价值日益受到瞩目。据统计数据显示,无人零售领域已吸引超过650亿元的投资注入。未来五年内,无人零售渠道在中国快消品市场有望迎来爆发性增长ÿ…
2024智能电网与能源系统国际学术会议(ICSGES2024)
2024智能电网与能源系统国际学术会议(ICSGES2024)
会议简介
我们诚挚邀请您参加将在南京隆重举行的2024年智能电网与能源系统国际学术会议(ICSGES2024)。南京,一座历史与现代交织的城市,将为这场盛会提供独特的学术…