问题描述
限量背包问题:从m个物品中挑选出最多v个物品放入容量为n的背包。
问题分析
限量背包问题,可以用来解决许多问题,例如要求从n个物品中挑选出最多v个物品放入容量为m的背包使得背包最后的价值最大,或者总共有多少种放法使得背包满载即组合数问题,又或者排列数问题。为了更好理解限量背包问题,我们先来回顾一下物品不限量的背包问题的滚动数组是如何写的。
01背包问题(物品每个只能选一次)
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
完全背包问题(物品每个可选多次)
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j=weight[i];j<=bagWeight[i];j++){// 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
从上面我们可以知道,如果物品只能选一次,则遍历背包容量从后往前,如果物品可以选多次,则遍历背包容量从前往后。
背包求组合数问题(从n个物品中选择放满背包有多少种组合)
dp[0]=1;
for(int i=0;i<n;i++){ // 遍历物品
for(int j=w[i];j<=m;j++){// 遍历背包容量
dp[j]+=dp[j-w[i]];
}
}
背包求排列数问题(从n个物品中选择放满背包有多少种排列)
dp[0]=1;
for(int j=1;j<=m;j++){ // 遍历物品
for(int i=0;i<n;i++){// 遍历背包容量
if(j>=w[i])
dp[j]+=dp[j-w[i]];
}
}
从上面我们又能知道,如果是求组合问题则是先遍历物品再遍历背包,如果是求排列问题则是先遍历背包再遍历物品。
回顾了以上这些知识点,接下来我们开始讲解限量背包的各种问题。限量背包相较于不限量背包不过是多了一层循环,和dp数组多了一个维度。多出来的这一个维度值i,表示选了i个物品的背包。如果要求从m个物品中挑选出最多v个物品放入容量为n的背包,则将1~v的dp数组值累加即可。
限量背包的各种问题
限量背包的01背包问题(物品每个只能选一次)
vector<vector<int> > dp(bagWeight+1,vector<int>(v+1,0));//v:最多可以放入v个物品
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
for(int k=1;k<=v;k++)//遍历每一个选择数量
dp[j][k]=max(dp[j][k],dp[j - weight[i]][k-1] + value[i]);//放入该物品与不放入该物品
}
}
限量背包的完全背包问题(物品每个可选多次)
vector<vector<int> > dp(bagWeight+1,vector<int>(v+1,0));//v:最多可以放入v个物品
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j=weight[i];j<=bagWeight[i];j++){ // 遍历背包容量
for(int k=1;k<=v;k++)//遍历每一个选择数量
dp[j][k]=max(dp[j][k],dp[j - weight[i]][k-1] + value[i]);//放入该物品与不放入该物品
}
}
限量背包求组合数问题(从n个物品中选择放满背包有多少种组合,物品可选多次)
vector<vector<int> > dp(n+1,vector<int>(v+1,0));//v:最多可以放入v个物品
dp[0][0]=1;
for(int i=0;i<m;i++){//遍历每个物品
for(int j=w[i];j<=n;j++){//遍历体积,从前往后遍历
for(int k=1;k<=v;k++){//遍历每一个选择数量
dp[j][k]+=dp[j-w[i]][k-1];
}
}
}
限量背包求组合数问题(从n个物品中选择放满背包有多少种组合,物品只能选一次)
vector<vector<int> > dp(n+1,vector<int>(v+1,0));//v:最多可以放入v个物品
dp[0][0]=1;
for(int i=0;i<m;i++){//遍历每个物品
for(int j=n;j>=w[i];j--){//遍历体积,从后往前遍历
for(int k=1;k<=v;k++){//遍历每一个选择数量
dp[j][k]+=dp[j-w[i]][k-1];
}
}
}
限量背包求排列数问题(从n个物品中选择放满背包有多少种排列,物品可选多次)
vector<vector<int> > dp(n+1,vector<int>(v+1,0));//v:最多可以放入v个物品
dp[0][0]=1;
for(int j=1;j<=n;j++){//遍历体积
for(int i=0;i<m;i++){//遍历每个物品
for(int k=1;k<=v;k++){//遍历每一个选择数量
if(j>=w[i])
dp[j][k]+=dp[j-w[i]][k-1];
}
}
}
限量背包求排列数问题(从n个物品中选择放满背包有多少种排列,物品只能选一次)很多同学看到这里肯定会想,既然知道了前面限量背包求排列数问题(物品可选多次)怎么写,那么这里是不是只需要将遍历体积的顺序改为从后往前就行了呢?答案是错误的。我这里给出一个测试结果
输入
第一行输入背包容量10,物品种类3,总选物品限量10
第二行输入每个物品的体积
输出
输出10行,第i行表示选i个物品的满载背包的选法的排列数。
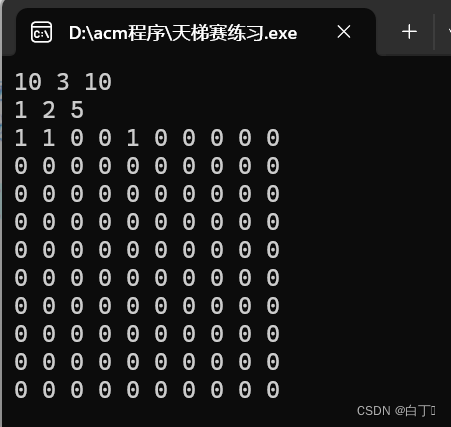
可以看到,第一行是对的,表示只选一个物品的背包的排列数,但是后面的全为0,这显然是错误的。那么应该如何解决这个问题呢?白丁暂时未能解决这个问题。如果有知道怎么写的大佬,欢迎发在评论区让我们学习学习。
限量背包的实际应用
2022——蓝桥杯十三届2022国赛大学B组真题