✨✨小新课堂开课了，欢迎欢迎~✨✨

🎈🎈养成好习惯，先赞后看哦~🎈🎈

所属专栏：http://t.csdnimg.cn/oHJAK（数据结构与算法）

小新的主页：编程版小新-CSDN博客

前言：今天我们主要从两个方面讲述环形链表，怎么判断是环形链表，以及如何如何找第一个入环的节点。

1.如何判断是否是环形链表

大家还记得如何找一个链表的中间节点吗？我们来回顾一下吧。

其中一种实现方法就是用的快慢指针，快指针每走两步，慢指针就走一步，当快指针对应的节点或者下一个节点为空时，慢指针指向该链表的中间节点。

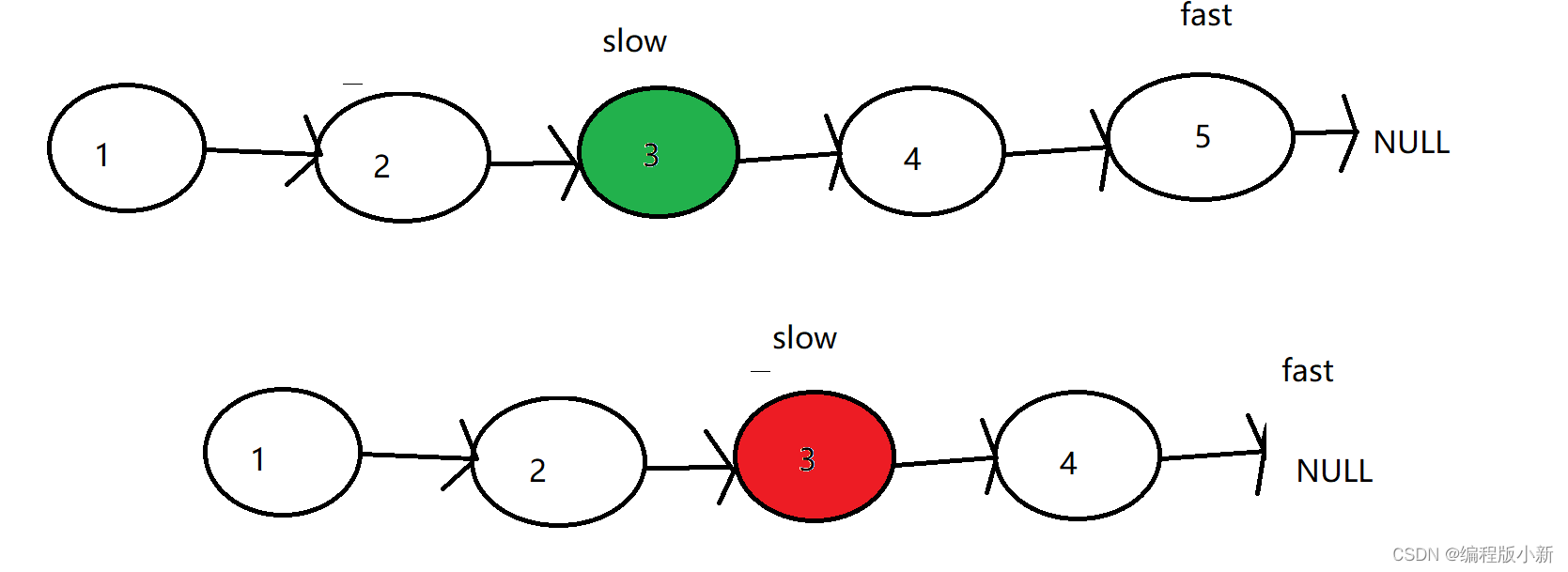
 这个是单链表的情况，如果这个链表是带环链表的话，快，慢指针都会进环。那么就会上演一场快，慢指针的追击大赛。如果追上就说明该链表带环，不然的话就像上面的单链表一样，还没有开始追就结束了。

小新：快，慢指针在环内一定会相遇吗？有没有刚好错过的可能？

           如果slow走一步，fast走3,4……n步呢，结果又会怎样？

下面我们就来解答这个疑问。

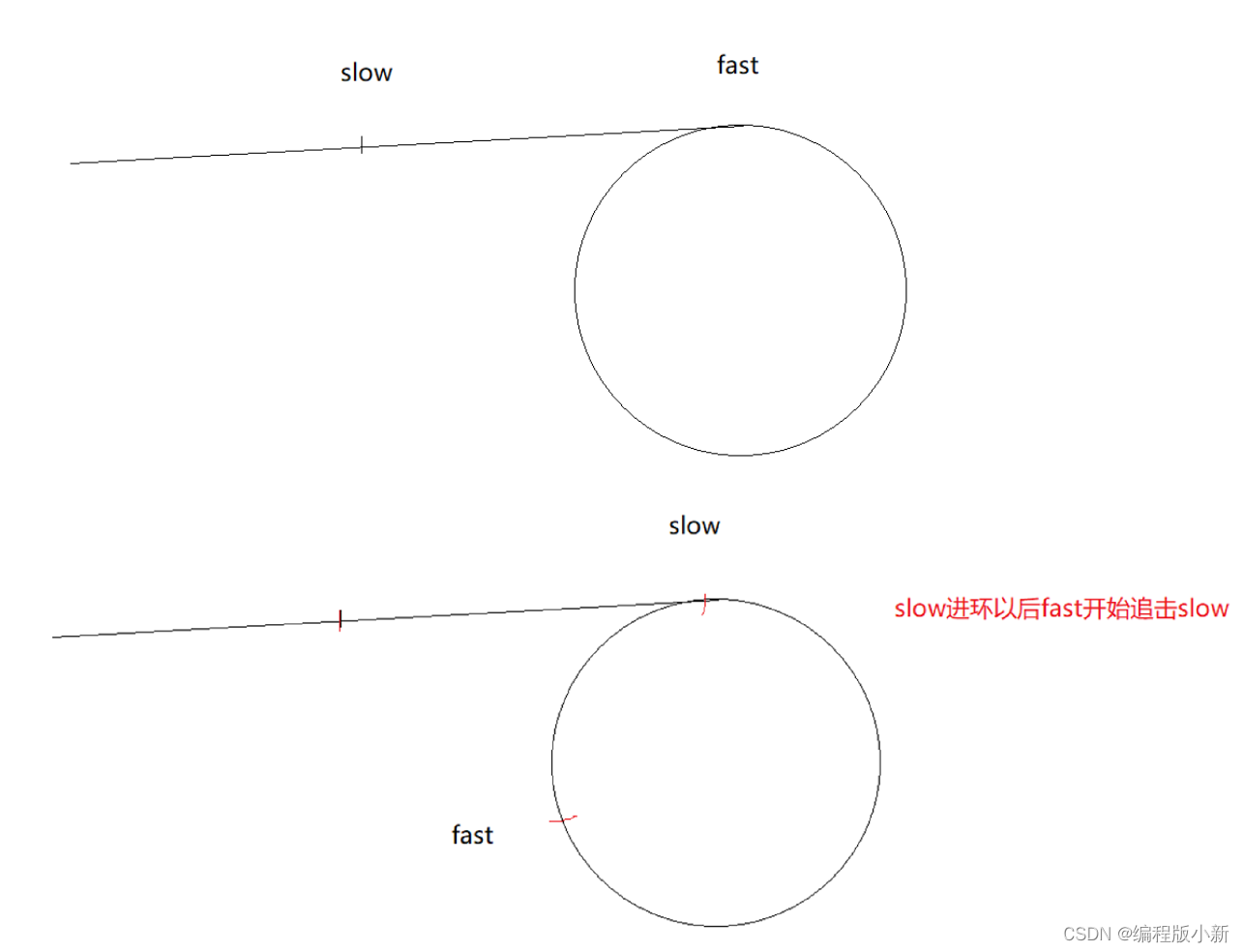
能不能追上，还需我们进一步的证明。

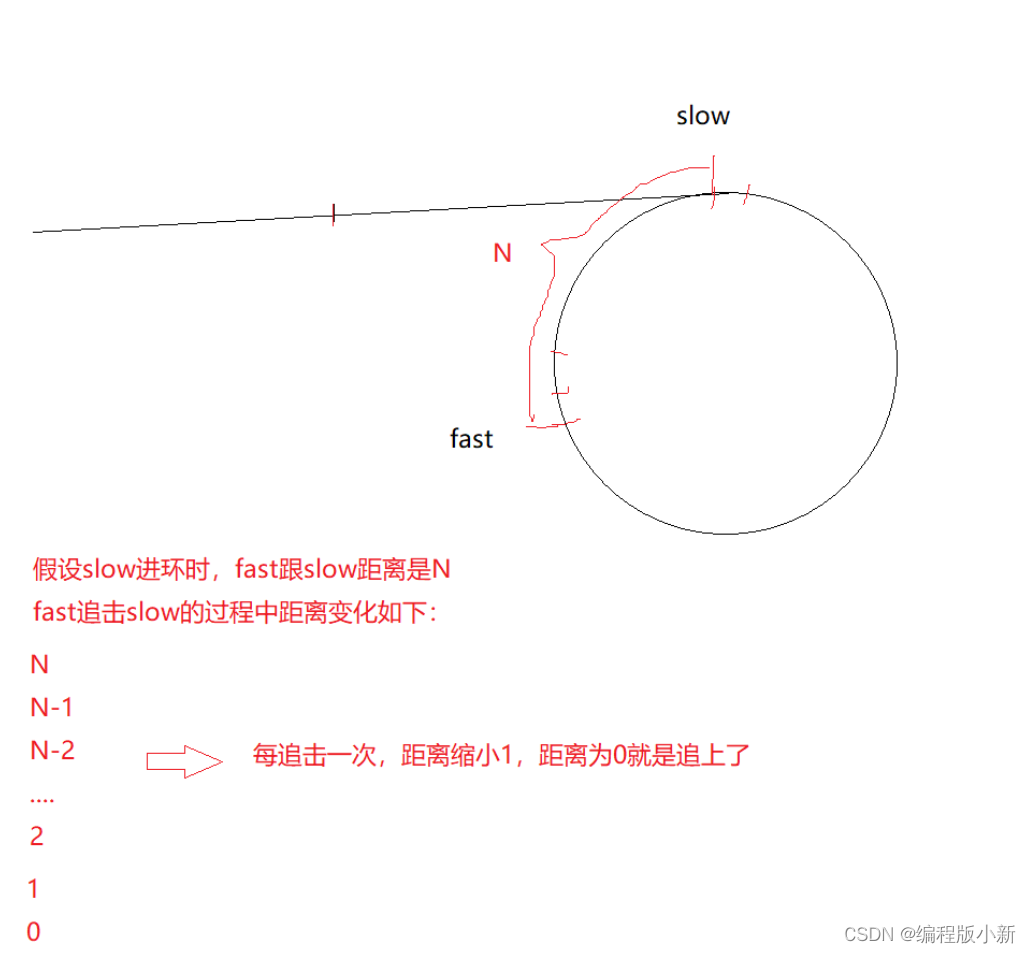
说明当fast走两步，slow走一步是能相遇的，刚好能证明该链表是一个带环链表。

那接下我们看fast走3步，slow走1步的情况。

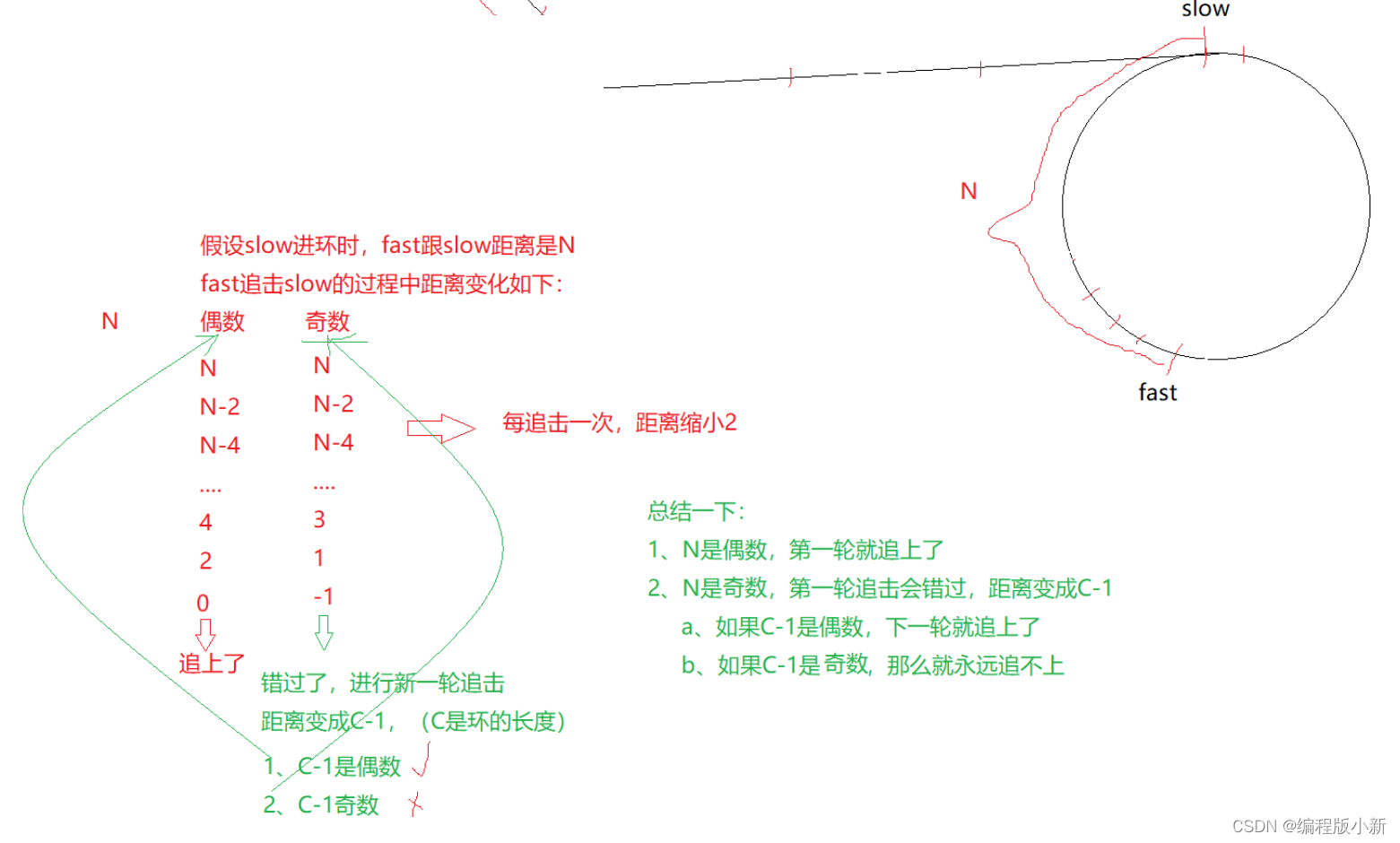 如果fast走4步，slow走一步

讨论方法还是像上面的一样，这样讨论下去是非常麻烦的。

根据上面的证明已经得出了一个结论： 当N时奇数，C是偶数时是永远追不上的，我们只需讨论有没有这种情况存在即可。

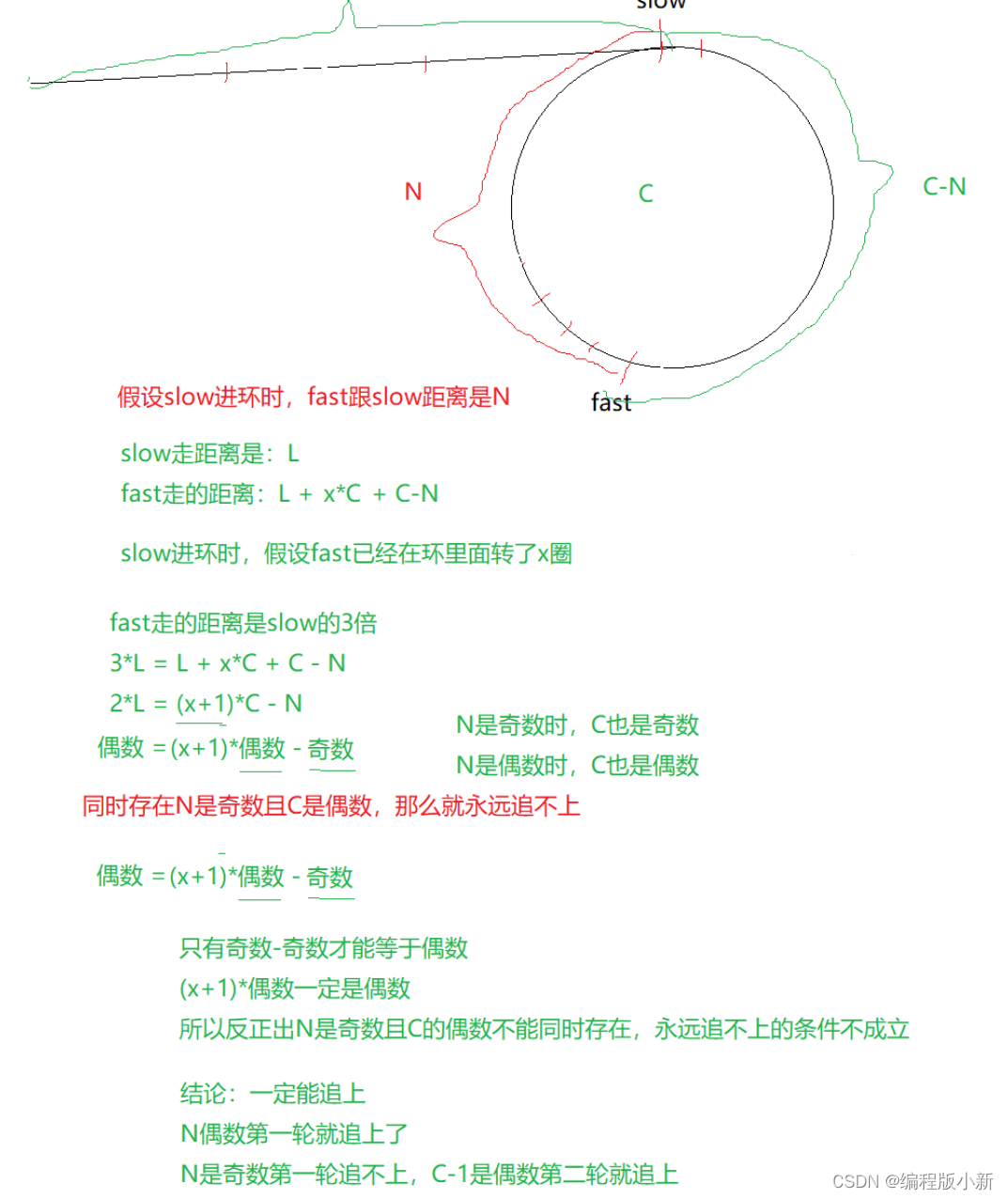
显然N是奇数，C是偶数的情况不存在 ，永远追不上的条件不成立，如果是带环链表的话是一定能追上的。

总结：当快指针走n步，慢指针走一步时，在带环链表中一定能相遇，与环的大小等其他因素有一定关系，但主要结论仍然成立。具体来说，虽然环的大小等因素会影响相遇的时间和具体过程，但由于快指针相对慢指针的速度优势，它们最终还是会在环中相遇。只是可能需要经过更多的步数或绕环更多圈才能相遇。

环形链表只需用快慢指针去证明，在环形链表中快慢指针一定会相遇。

2.如何找到第一个入环的节点 

前面我们已经知道，快慢指针会在环形链表中相遇。

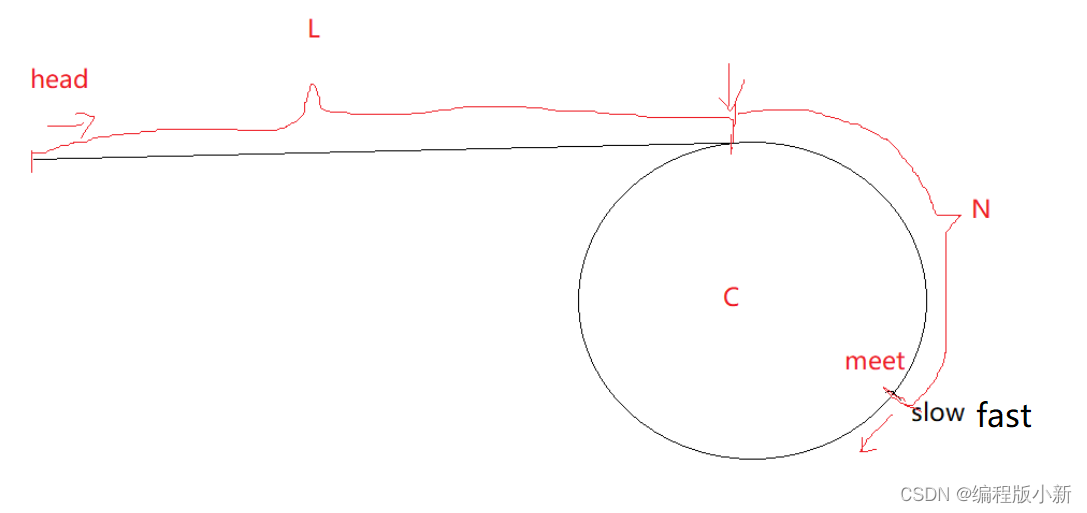
这个相遇的结论除了能证明链表是环形链表外，还能帮助找到的第一个入环的节点。

 这里以fast走2步，slow走一步为例。

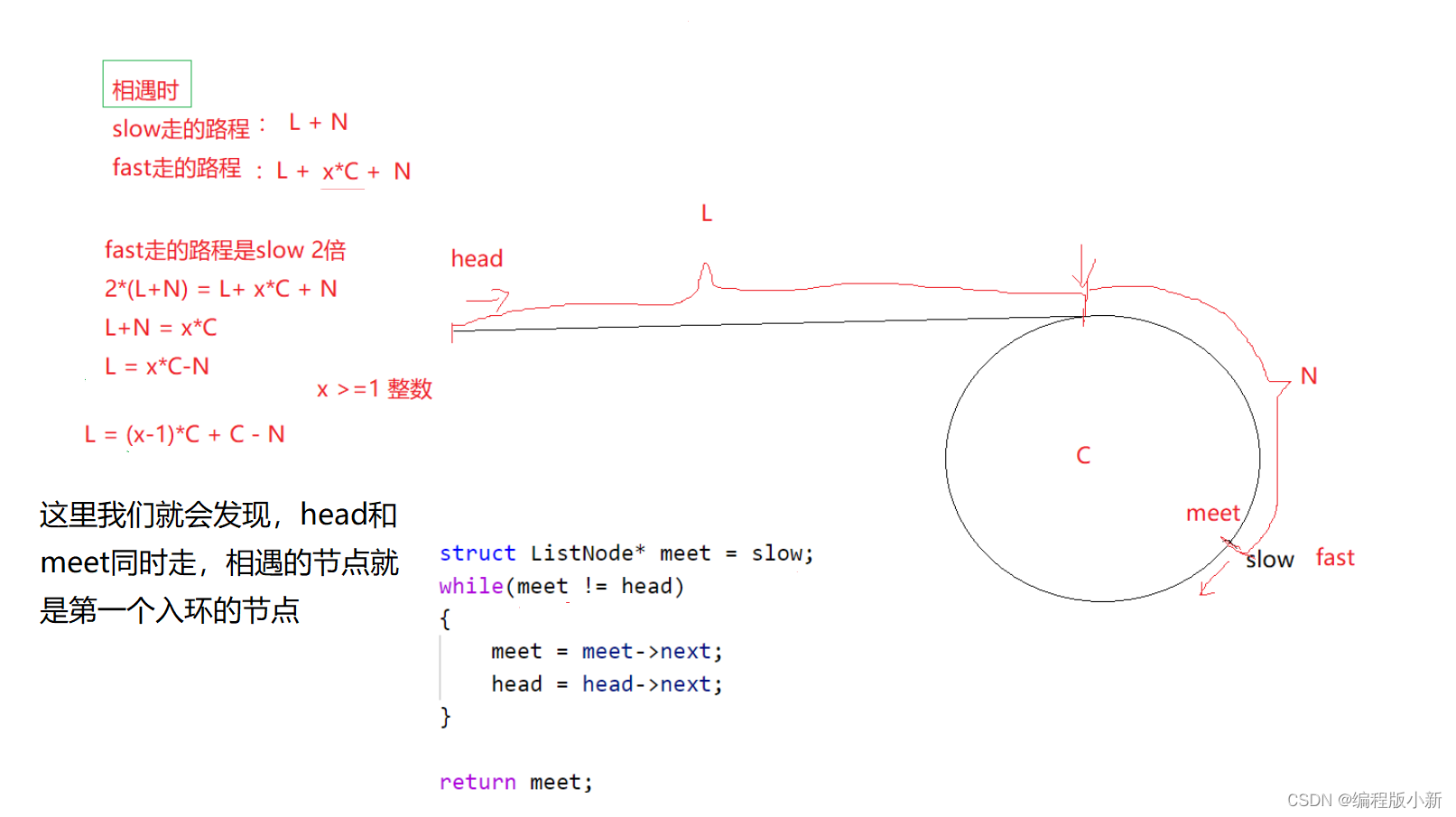
3.实战练习 

示例1：判断是否为环形链表

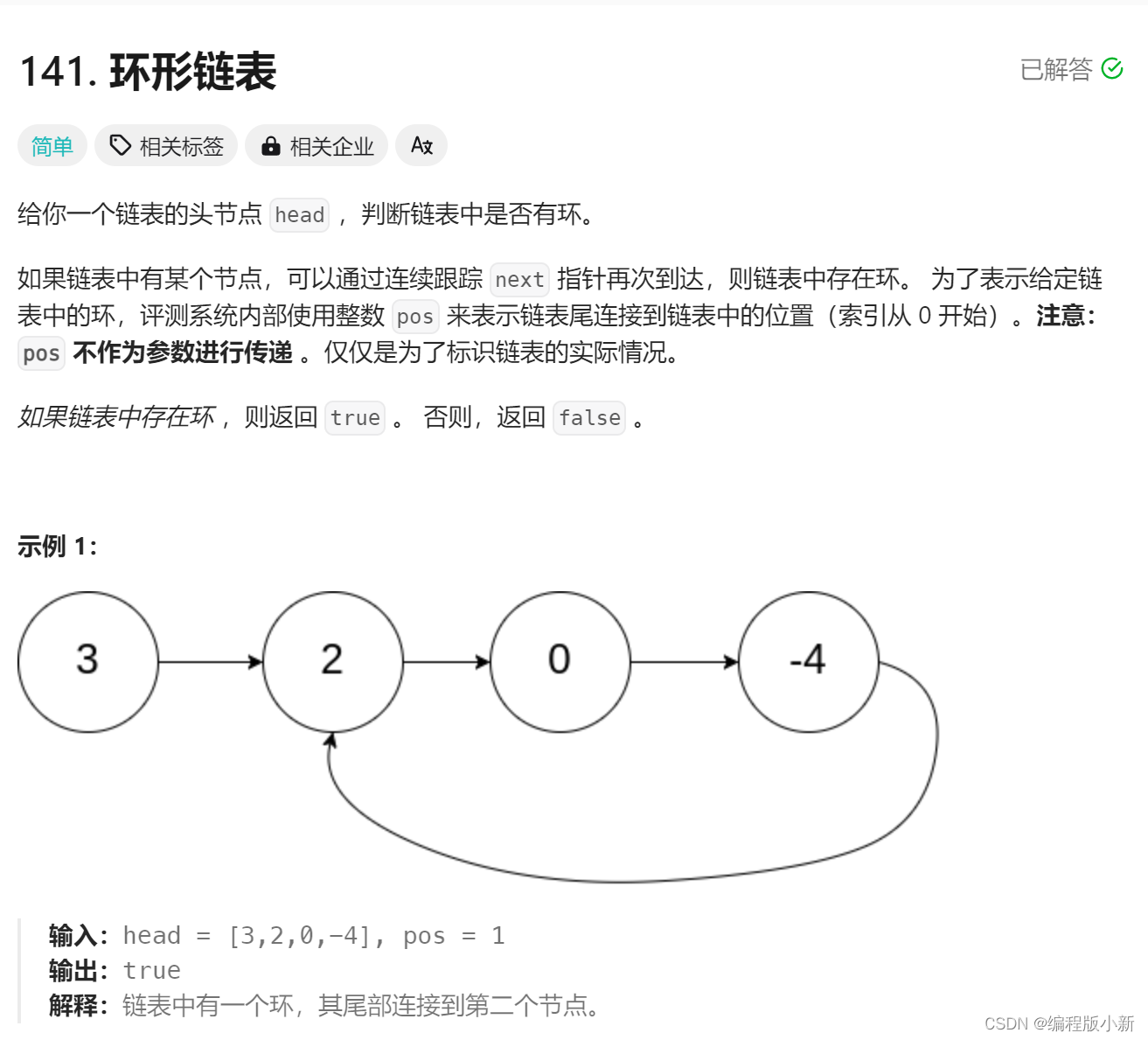
代码实现：

bool hasCycle(struct ListNode *head) {
    struct ListNode* fast,*slow;
    fast=slow=head;
    while(fast && fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(fast==slow)
        return true;
    }

    return false;
}

示例二：找第一个入环节点

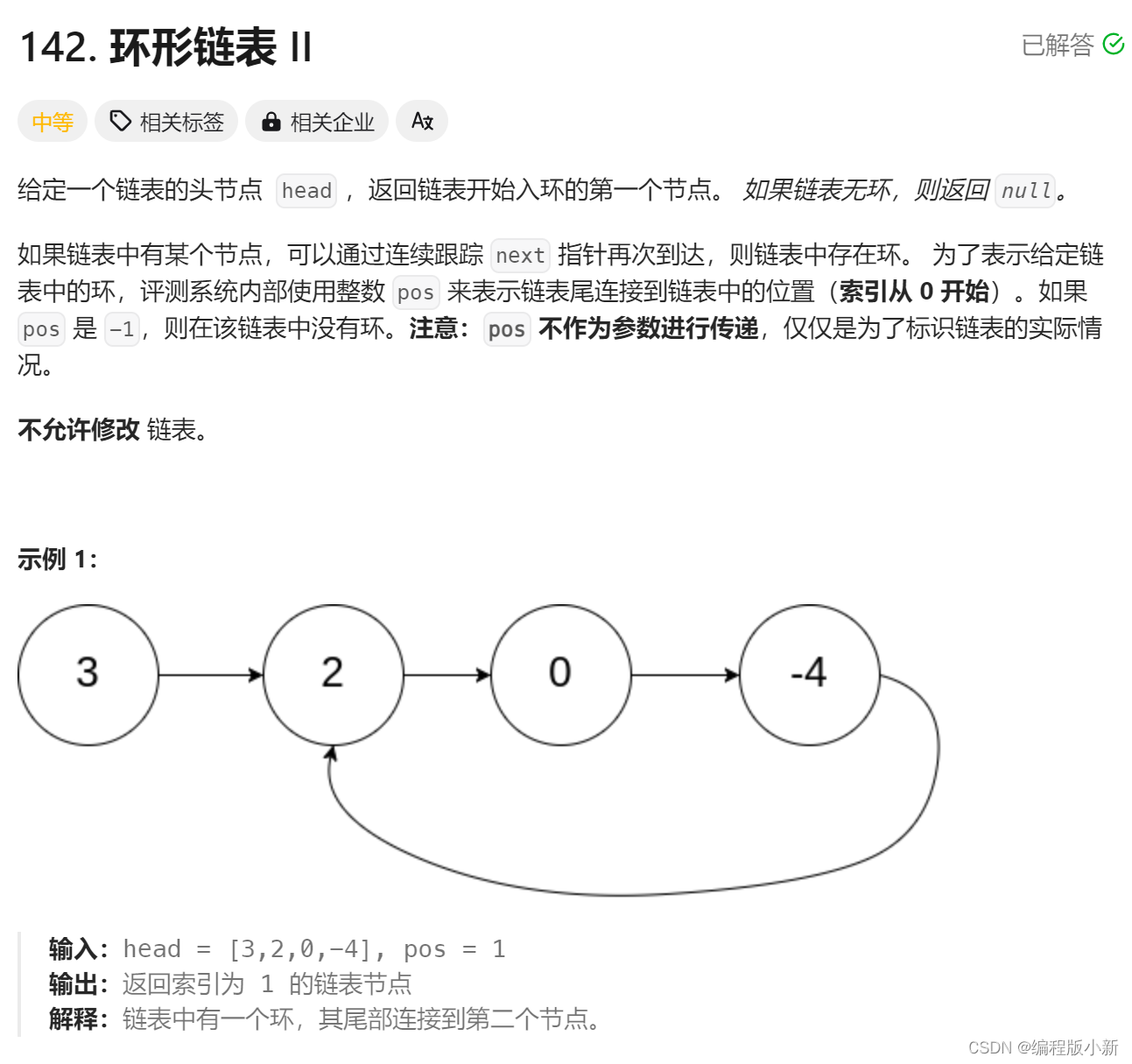
代码实现：

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode* fast, * slow;
fast = slow = head;
while (fast && fast->next)
{
    slow = slow->next;
    fast = fast->next->next;
    //相遇
    if (fast == slow)
    {
        struct ListNode* meet = slow;
        while (head != meet)
        {
            head = head->next;
            meet = meet->next;
        }
        return meet;
    }

}

return NULL;
}

 结束了~

下次还记得来哦