一、概念
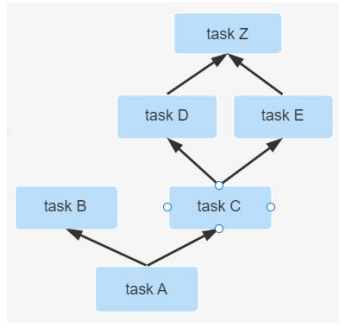
二叉搜索树也叫二叉排序树。在一颗二叉搜索树中,他的左子树二点节点值一定比根节点的值小,他的右子树节点的值一定比根节点的值大。
二、特点
他的左子树节点的值一定比根节点的值小
他的右子树节点的值一定比根节点的值大
他的每一颗子树都是一颗二叉搜索树
他的查找效率很高,类似二分查找O(logn)
三、代码实现
- 准备字段
需要准备的有二叉树的节点类跟根节点
public class BinaryTree {
static class TreeNode {
public int val; //节点的值
public TreeNode left;//左孩子地址
public TreeNode right;//右孩子地址
public TreeNode(int val) {
this.val = val;
}
}
public TreeNode root; //根节点
}2.查找
二叉搜索树里的查找很简单,我们拿要查找的值鱼根节点进行比较,如果比根节点大就去根节点的右子树查找,如果比根节点小就去根节点的左边查找,如果相等就返回根节点。
public class BinaryTree {
static class TreeNode {
public int val; //节点的值
public TreeNode left;//左孩子地址
public TreeNode right;//右孩子地址
public TreeNode(int val) {
this.val = val;
}
}
public TreeNode root; //根节点
/**
* 查找返回找到的节点
* @param key
* @return
*/
public TreeNode search(int key){
//定义一个节点代替根节点去遍历查找
TreeNode cur = root;
//循环查找
while (cur != null) {
if (cur.val < key) {
//如果key的值比根节点的值大就去右子树查找
cur = cur.right;
} else if (cur.val > key) {
//如果key的值比根节点的值大就去左子树查找
cur = cur.left;
} else {
//说明找到了,就返回节点
return cur;
}
}
//没找到返回空
return null;
}
}- 插入
我们先构造一颗二叉搜索树,然后在这棵树里分别插入元素8,9,0


插入8:比3大在右子树找合适的位置,比4的往右,比5大往右插入到5的右边
9跟0类似,我们发现每次插入的元素都会到叶子节点,于是我们只需要找到合适的叶子节点,然后再判断插入叶子节点的左边还是右边
public void insert(int val){
//创建节点
TreeNode node = new TreeNode(val);
//创建节点代替跟节点遍历找到合适位置,并记录父亲节点的位置
TreeNode parent = null;
TreeNode cur = root;
//遍历
while (cur != null){
if(cur.val < val){
//去右子树
parent = cur;
cur = cur.right;
}else if(cur.val > val){
//去左子树
parent = cur;
cur = cur.left;
}else {
//说明已经存在值了,直接返回
return;
}
}
//此时cur = null parent指向的位置就是要插入的叶子节点
if(parent.val < val) {
//说明比该叶子节点值大,插入右边
parent.right = node;
}else {
//插入左边
parent.left = node;
}
}- 删除
删除操作就需要进行分类:如果要删除的节点没有左孩子;如果要删除的节点没有右孩子;如果要删除的节点有左右孩子
- 待删节点没有左孩子
当我们找到这个节点后发现他没有左孩子,此时我们有需要进行讨论:这个节点是不是根节点;这个节点是他父亲节点的左孩子;这个节点是他父亲节点的右孩子。
- 跟节点
他是跟节点时,由于没有左孩子,所以直接让跟节点的右孩子指向跟节点的右孩子

- 是父亲的左孩子
他是父亲节点的左孩子且他没有左孩子,所以此时直接让父亲节点的左孩子指向这个节点的右孩子
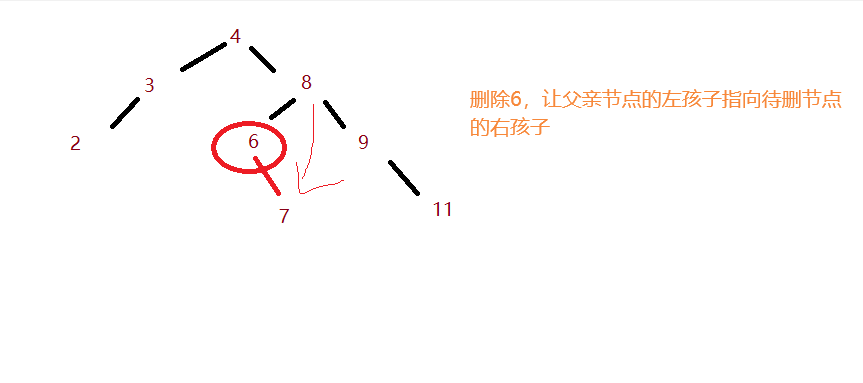
- 是父亲的右孩子
他是父亲节点的右孩子且他没有左孩子,所以此时直接让父亲节点的右孩子指向这个节点的右孩子

- 待删节点没有右孩子
当我们找到这个节点后发现他没有右孩子,此时我们有需要进行讨论:这个节点是不是根节点;这个节点是他父亲节点的左孩子;这个节点是他父亲节点的右孩子。
- 跟节点
是根节点且没有右孩子,说明只有左孩子,删除根节点只需要将根节点指向根节点的左孩子
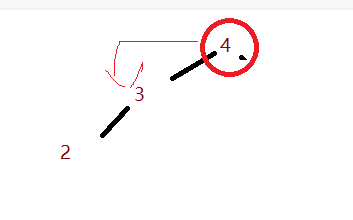
- 是父亲的左孩子
由于待删节点没有右孩子,所以直接让他的父亲的左边指向待删节点的左孩子

- 是父亲的右孩子
由于待删节点没有右孩子,所以直接让父亲的右边指向待删节点的左孩子

- 待删节点有左右孩子
当既有左孩子又有右孩子时,我们此时使用替换删除,也就是在待删节点的左子树去找最大值(左子树的最右边)或者右子树的最小值(右子树的最左边)找到后,与待删节点的值进行交换后删除找到的该节点

public void remove(int key){
//先找到该节点与其父亲节点
TreeNode cur = root;
TreeNode parent = null;
while (cur != null){
if(cur.val < key){
parent = cur;
cur = cur.right;
}else if(cur.val > key){
parent = cur;
cur = cur.left;
}else {
//找到进行删除
delete(parent,cur);
return;
}
}
}
private void delete(TreeNode parent, TreeNode cur) {
if(cur.left == null){
//没有左子树
if(cur == root){
//如果是跟节点
root = root.right;
}else if(cur == parent.left){
//是父亲的左子树
parent.left = cur.right;
}else {
//是父亲的右子树
parent.right = cur.right;
}
}else if (cur.right == null){
//没有右子树
if (cur == root){
//是根节点
root = root.left;
}else if(cur == parent.left){
//是父亲节点的左子树
parent.left = cur.left;
}else {
//是父亲节点的右子树
parent.right = cur.right;
}
}else {
//此时既有左又有右:去右边找最小值,也就是右子树的最左边
TreeNode target = cur.right;
TreeNode targetParent = cur;
while (target.left != null){
targetParent = target;
target = target.left;
}
//找到了交换值
cur.val = target.val;
//删除target:处理特殊情况下面说明
if(target == targetParent.left){
targetParent.left = target.right;
}else {
targetParent.right = target.right;
}
}
}特殊情况:当去右子树里找最小值时,每一个子树没有左子树的时候,此时待删节点的右边第一个就是最小值,这种情况删除时需要注意