极大极小游戏

难度：简单

给你一个下标从 0 开始的整数数组 nums ，其长度是 2 的幂。

对 nums 执行下述算法：

设 n 等于 nums 的长度，如果 n == 1 ，终止 算法过程。否则，创建 一个新的整数数组 newNums ，新数组长度为 n / 2 ，下标从 0 开始。
对于满足 0 <= i < n / 2 的每个 偶数 下标 i ，将 newNums[i] 赋值 为 min(nums[2 * i], nums[2 * i + 1]) 。
对于满足 0 <= i < n / 2 的每个 奇数 下标 i ，将 newNums[i] 赋值 为 max(nums[2 * i], nums[2 * i + 1]) 。
用 newNums 替换 nums 。

从步骤 1 开始 重复 整个过程。
执行算法后，返回 nums 中剩下的那个数字。

示例 1：

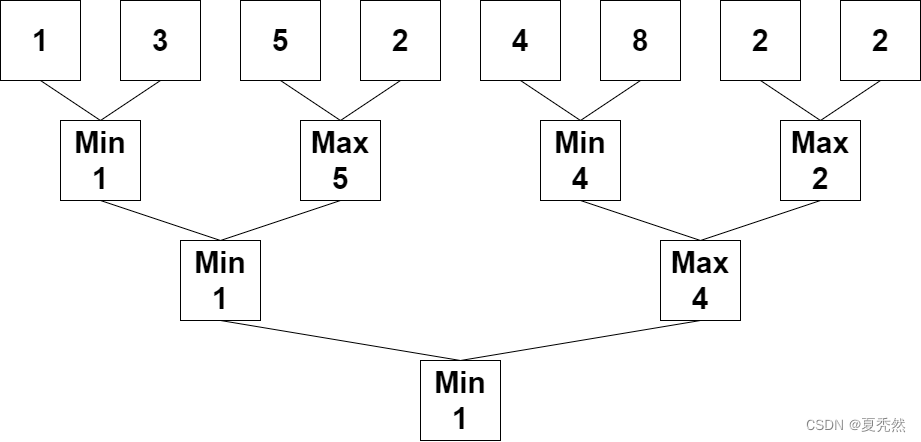
输入：nums = [1,3,5,2,4,8,2,2]
输出：1
解释：重复执行算法会得到下述数组。
第一轮：nums = [1,5,4,2]
第二轮：nums = [1,4]
第三轮：nums = [1]
1 是最后剩下的那个数字，返回 1 。

示例 2：

输入：nums = [3]
输出：3
解释：3 就是最后剩下的数字，返回 3 。

解法一、模拟

思路：

我们用一个循环来模拟整个过程，循环的条件是 $n\ne 1$，其中 $n$ 是 $\text{nums}$ 的长度。循环内，我们按照题意求出 $\text{newNums}$，然后用 $\text{newNums}$ 替换 $\text{nums}$ 即可。最后返回 $\text{nums}[0]$ 作为答案。

复杂度分析：

• 时间复杂度： $O(n)$，其中 $n$ 是数组 $\text{nums}$ 的长度。第一次循环的时间复杂度为 $O(n)$，下一次循环时问题规模减半，所以总体复杂度为 $O(n)+O(\frac{n}{2})+O(\frac{n}{4})+\cdots +O(1)=O(n)$
• 空间复杂度： $O(n)$，其中 $n$ 是数组 $\text{nums}$ 的长度。

class Solution:
    def minMaxGame(self, nums: List[int]) -> int:
        while len(nums) != 1:
            res, index = list(), 0 
            while index < len(nums):
                if int(index / 2) % 2 == 0:
                    res.append(min(nums[index], nums[index + 1]))
                else:
                    res.append(max(nums[index], nums[index + 1]))
                index += 2
            nums = res.copy()
        return nums[0]

解法二、原地修改

思路：

注意到在顺序遍历的情况下，$\text{newNums}[i]$ 的计算结果可以直接存储到 $\text{nums}[i]$ 中。这是因为 $\text{nums}[i]$ 早在计算 $\text{newNums}[\lfloor \frac{i}{2}\rfloor ]$ 时就已经被使用，而且它在未来一定不会再被使用。有一个特例是 $i=0$，但此时可以原地修改的原因是很显然的。

复杂度分析：

• 时间复杂度： $O(n)$，其中 $n$ 是数组 $\text{nums}$ 的长度。第一次循环的时间复杂度为 $O(n)$，下一次循环时问题规模减半，所以总体复杂度为 $O(n)+O(\frac{n}{2})+O(\frac{n}{4})+\cdots +O(1)=O(n)$。
• 空间复杂度： $O(1)$。

class Solution:
    def minMaxGame(self, nums: List[int]) -> int:
        length = len(nums)
        while length != 1:
            index, now = 0, 0
            while index < length:
                if int(index / 2) % 2 == 0:
                    nums[now] = min(nums[index], nums[index + 1])
                else:
                    nums[now] = max(nums[index], nums[index + 1])
                index += 2
                now += 1
            length //= 2
        return nums[0]

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/min-max-game