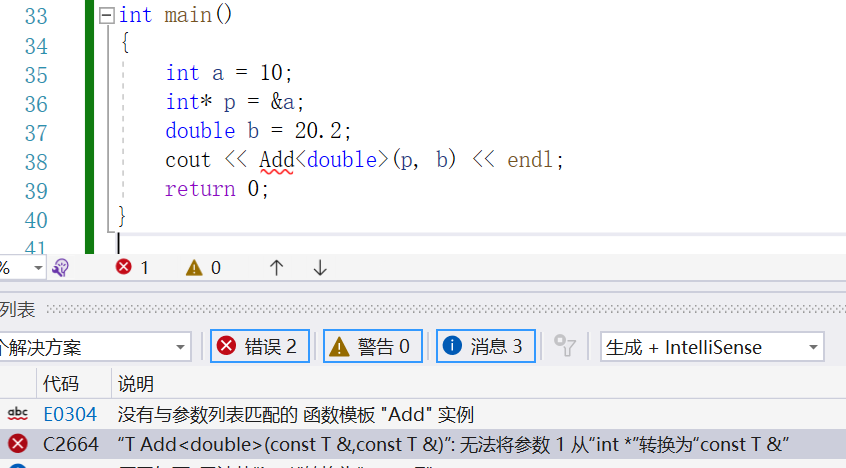
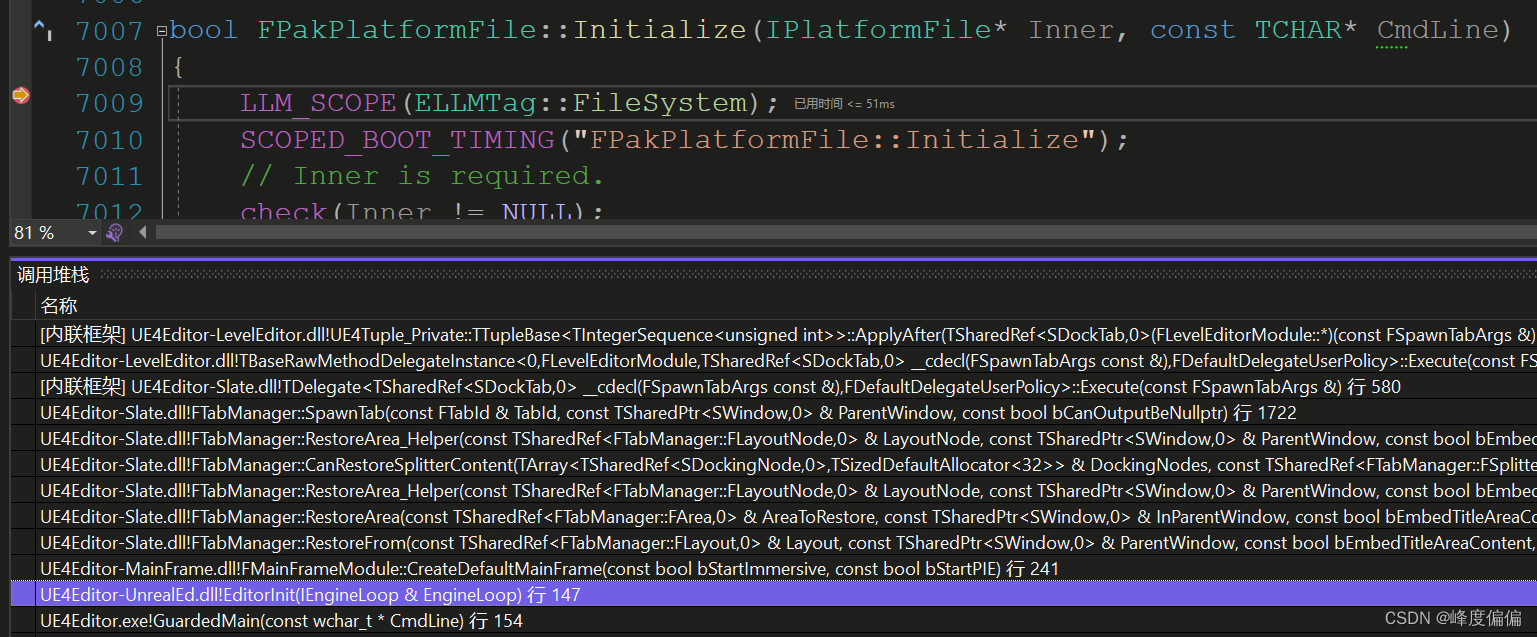
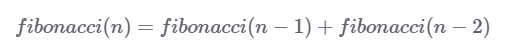使用场景

        动态规划最重要的是转移方程，而转移方程需要递归和记忆化搜索产生的表，因此直接贴出转移方程是没什么用的，不探究如何从递归到记忆化搜索再到转移方程，还是很难想到怎么去得到转移方程。下面我们将从例子中探寻如何三步走。

动态规划和递归的区别

1.递归是从上而下（从大问题到小问题），而动态规划是由下而上（先解决小问题最后到大问题）；
2.动态规划会储存每个小问题的结果，从而它的计算速度会比递归要快。（代价是动态规划的空间复杂度更高，即用空间换取的时间）。

 实例：斐波那契数列

 递归算法：

    public int Fibonacci(int n) {
       if(n == 0 || n == 1){
            return n;
       }
        return Fibonacci(n - 1) + Fibonacci(n - 2);
    }

 动态规划：

    public int Fibonacci(int n) {
        int dp[10000];        //设n最大为9999
        dp[0] = 0;
        dp[1] = 1;
        for(int i = 2;i < n;i++){
            dp[i] = dp[i - 1] + dp[i - 2];    
        }
        return dp[n - 1];        //dp[n - 1]代表n对应的值
    }

例题

（1）例一

题目：

最长递增子序列

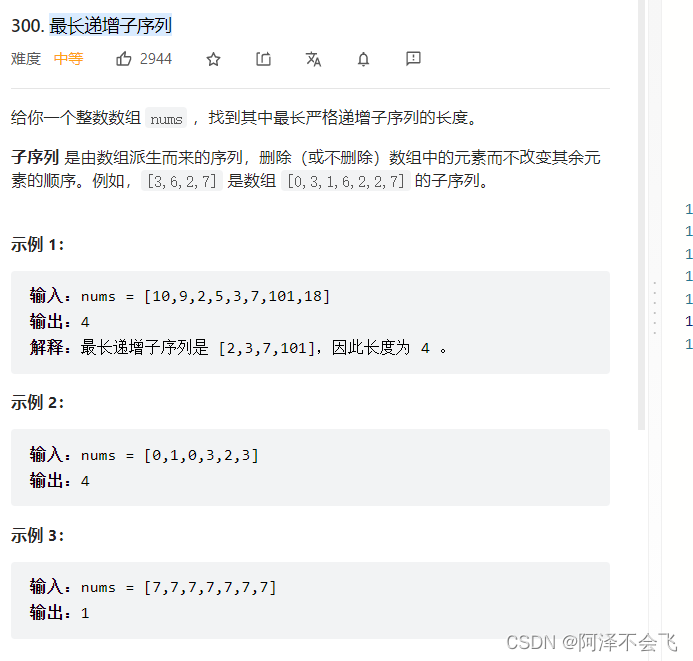
解题思想：

建立一个长度相同的数组，数组记录i之前贴合条件的最大数，用双重for循环进行查找

代码：

// Dynamic programming.
class Solution {
    public int lengthOfLIS(int[] nums) {
        if(nums.length == 0) return 0;
        int[] dp = new int[nums.length];
        int res = 0;
        Arrays.fill(dp, 1);
        for(int i = 0; i < nums.length; i++) {
            for(int j = 0; j < i; j++) {
                if(nums[j] < nums[i]) dp[i] = Math.max(dp[i], dp[j] + 1);
            }
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

 （1）例二

题目：

“蓝桥杯”练习系统（拿金币）

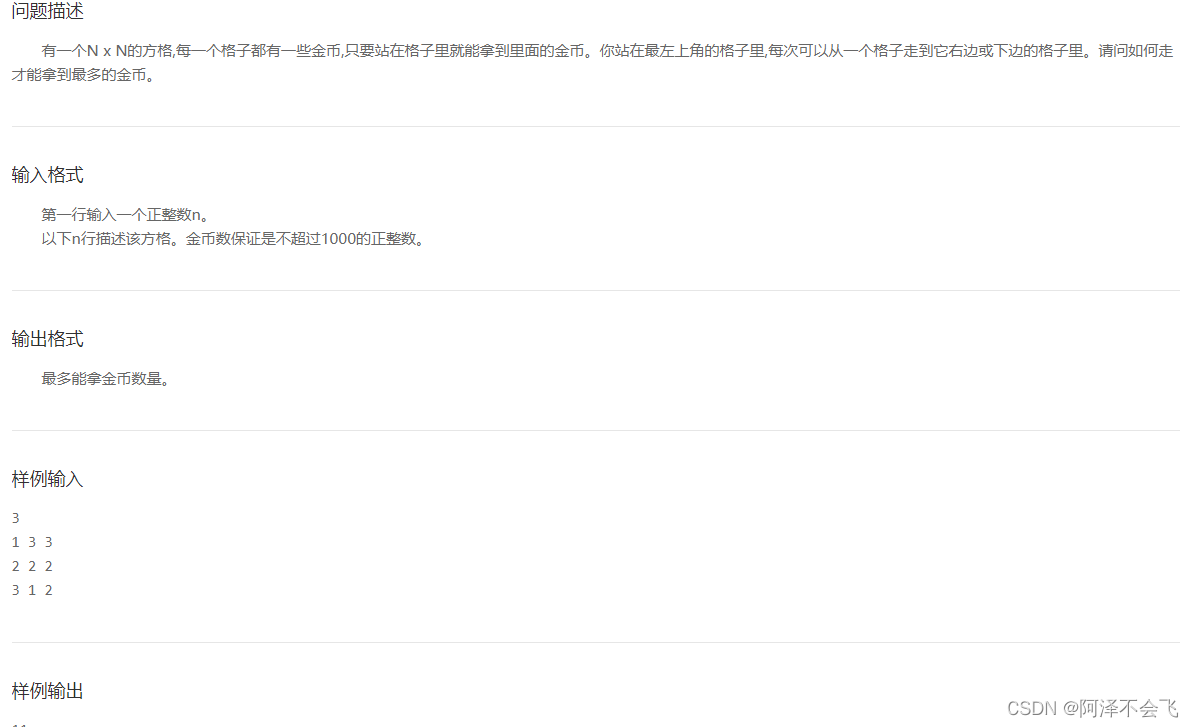
解题思想：

建立一个长高度相同的数组，数组内每个元素代表着到这个元素可采集的最大金币量，先根据题意把新数组的第一行和列遍历出来，然后动态规划，得出其他的元素

代码：

import java.util.Scanner;
class Main{
	public static void main(String[] args) {
		Scanner in=new Scanner(System.in);
		int n=in.nextInt();
		int[][] beginarr=new int[n][n];
		for(int i=0;i<n;i++) {
			for(int j=0;j<n;j++) {
				beginarr[i][j]=in.nextInt();
			}
		}
		int[][] endarr=new int[n][n];
		endarr[0][0]=beginarr[0][0];
		for(int i=1;i<n;i++) {
			endarr[0][i]=beginarr[0][i]+endarr[0][i-1];
			endarr[i][0]=beginarr[i][0]+endarr[i-1][0];
		}
		for(int i=1;i<n;i++) {
			for(int j=1;j<n;j++) {
				endarr[i][j]=beginarr[i][j]+Math.max(endarr[i-1][j], endarr[i][j-1]);
			}
		}
		System.out.println(endarr[n-1][n-1]);
	}
}