基于鸢尾花数据集的四种聚类算法（kmeans，层次聚类，DBSCAN,FCM）和学习向量量化对比

news2024/10/6 10:33:06

基于鸢尾花数据集的四种聚类算法（kmeans，层次聚类，DBSCAN,FCM）和学习向量量化对比

注：下面的代码可能需要做一点参数调整，才得到所有我的运行结果。

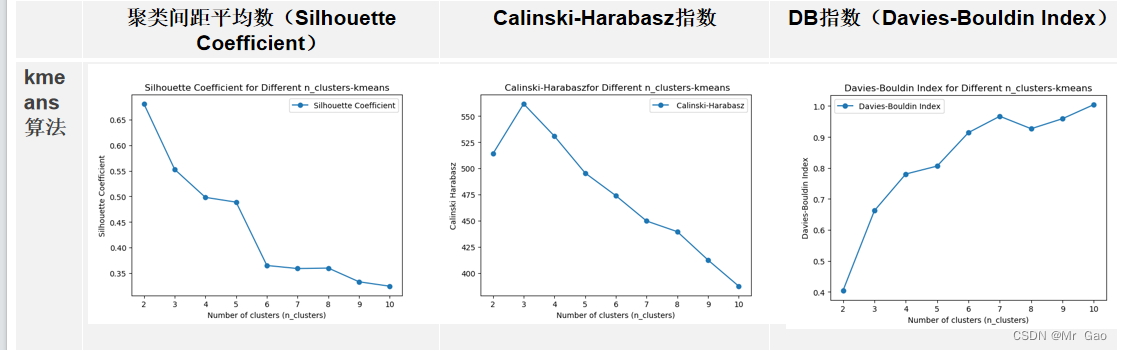
kmeans算法：

import matplotlib.pyplot as plt # 导入matplotlib的库
import numpy as np # 导入numpy的包
from sklearn import datasets #导入数据集
from sklearn.decomposition import PCA # PCA主成分分析类
from sklearn.metrics import silhouette_score
from sklearn.metrics import calinski_harabasz_score
from sklearn.metrics import davies_bouldin_score
iris = datasets.load_iris() #加载iris数据集
X = iris.data #加载特征数据
# Y = iris.target #加载标签数据
#绘制数据分布图
y = iris.target
X = iris.data
#X.shape
#调用PCA
pca = PCA(n_components=2) # 降到2维
pca = pca.fit(X) #拟合模型
X_dr = pca.transform(X) #获取新矩阵 （降维后的）
#X_dr



#也可以fit_transform一步到位
#X_dr = PCA(2).fit_transform(X)


#plt.figure()
#plt.scatter(X_dr[y==0, 0], X_dr[y==0, 1], c="red", label=iris.target_names[0]) 
#plt.scatter(X_dr[y==1, 0], X_dr[y==1, 1], c="black", label=iris.target_names[1])
#plt.scatter(X_dr[y==2, 0], X_dr[y==2, 1], c="orange", label=iris.target_names[2])
#plt.legend()
#plt.title('PCA of IRIS dataset')
#plt.show()


print("===K-means聚类===")
from sklearn.cluster import KMeans # 引入KMeans模块


estimator = KMeans(n_clusters=3).fit(X)  # 构造聚类器
label_pred = estimator.labels_  # 获取聚类标签

# 评估指标列表  
silhouette_avg_scores = []  
  
Calinski_Harabasz_scores = []  
Davies_Bouldin_scores = []  
# 遍历不同的n_clusters值  
for n_clusters in range(2, 11):  
    kmeans = KMeans(n_clusters=n_clusters)  
    kmeans.fit(X)  
    labels = kmeans.labels_  
    silhouette_avg = silhouette_score(X, kmeans.labels_)  
    print(silhouette_avg)
# 2. Calinski-Harabasz指数
    calinski_haraba=calinski_harabasz_score(X, kmeans.labels_)
    print(calinski_haraba)
 
    # 3. DB指数（Davies-Bouldin Index）
    davies_bouldin=davies_bouldin_score(X, kmeans.labels_)
    Davies_Bouldin_scores.append(davies_bouldin)
    Calinski_Harabasz_scores.append(calinski_haraba)
    silhouette_avg_scores.append(silhouette_avg)  
  
# 绘制图形  
plt.plot(range(2, 11), silhouette_avg_scores, marker='o', label='Silhouette Coefficient')  

plt.title('Silhouette Coefficient for Different n_clusters-kmeans')  
plt.xlabel('Number of clusters (n_clusters)')  
plt.ylabel('Silhouette Coefficient')  
plt.legend()
plt.show()
 
plt.plot(range(2, 11), Calinski_Harabasz_scores, marker='o', label=' Calinski-Harabasz')  
plt.title(' Calinski-Harabaszfor Different n_clusters-kmeans')  
plt.xlabel('Number of clusters (n_clusters)')  
plt.ylabel('Calinski Harabasz')  
plt.legend()
plt.show()

  
plt.plot(range(2, 11), Davies_Bouldin_scores, marker='o', label='Davies-Bouldin Index')  
plt.title('Davies-Bouldin Index for Different n_clusters-kmeans')  
plt.xlabel('Number of clusters (n_clusters)')  
plt.ylabel('Davies-Bouldin Index')  
plt.legend()
plt.show()

运行结果如下：
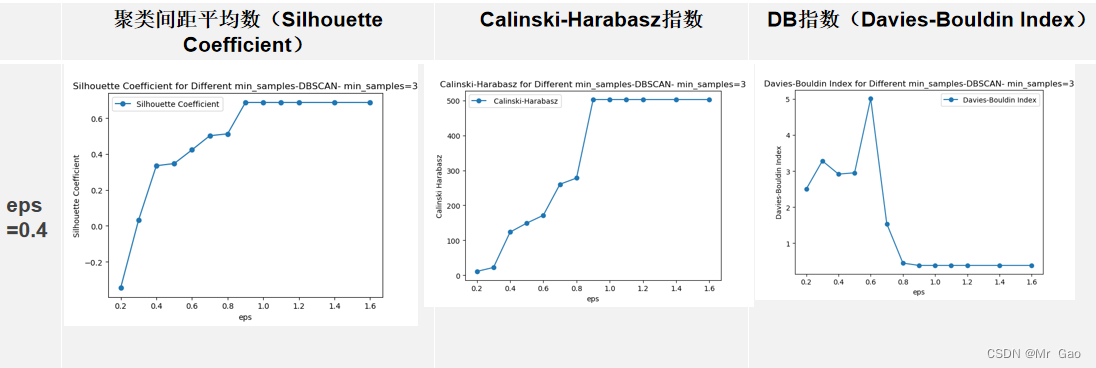
在这里插入图片描述

DBSCAN:

import matplotlib.pyplot as plt # 导入matplotlib的库
import numpy as np # 导入numpy的包
from sklearn import datasets #导入数据集
from sklearn.decomposition import PCA # PCA主成分分析类
from sklearn.metrics import silhouette_score
from sklearn.metrics import calinski_harabasz_score
from sklearn.metrics import davies_bouldin_score

from sklearn.cluster import DBSCAN # 引入DBSCAN模块

iris = datasets.load_iris() #加载iris数据集
X = iris.data #加载特征数据
# Y = iris.target #加载标签数据
#绘制数据分布图
y = iris.target
X = iris.data
#X.shape
##调用PCA
#pca = PCA(n_components=2) # 降到2维
#pca = pca.fit(X) #拟合模型
#X_dr = pca.transform(X) #获取新矩阵 （降维后的）
##X_dr



#也可以fit_transform一步到位
#X_dr = PCA(2).fit_transform(X)


#plt.figure()
#plt.scatter(X_dr[y==0, 0], X_dr[y==0, 1], c="red", label=iris.target_names[0]) 
#plt.scatter(X_dr[y==1, 0], X_dr[y==1, 1], c="black", label=iris.target_names[1])
#plt.scatter(X_dr[y==2, 0], X_dr[y==2, 1], c="orange", label=iris.target_names[2])
#plt.legend()
#plt.title('PCA of IRIS dataset')
#plt.show()


print("===DBSCAN聚类===")
from sklearn.cluster import KMeans # 引入KMeans模块


estimator = KMeans(n_clusters=3).fit(X)  # 构造聚类器
label_pred = estimator.labels_  # 获取聚类标签

# 评估指标列表  
silhouette_avg_scores = []  
  
Calinski_Harabasz_scores = []  
Davies_Bouldin_scores = []  
# 遍历不同的n_clusters值  
for n_clusters in range(2, 11):  
    dbscan = DBSCAN(eps=0.4, min_samples=n_clusters).fit(X) #导入DBSCAN模块进行训练,在一个邻域的半径内min_samples数的邻域eps被认为是一个簇。请记住，初始点包含在min_samples中。
    label_pred = dbscan.labels_ # labels为每个数据的簇标签,不在任何“高密度”集群中的“noisy”样本返回-1
    silhouette_avg = silhouette_score(X, dbscan.labels_)  
    print(silhouette_avg)

  
 
# 2. Calinski-Harabasz指数
   
    calinski_haraba=calinski_harabasz_score(X, dbscan.labels_)
    print(calinski_haraba)
 
    # 3. DB指数（Davies-Bouldin Index）
    davies_bouldin=davies_bouldin_score(X, dbscan.labels_)
    Davies_Bouldin_scores.append(davies_bouldin)
    Calinski_Harabasz_scores.append(calinski_haraba)
    silhouette_avg_scores.append(silhouette_avg)  
  
# 绘制图形  
plt.plot(range(2, 11), silhouette_avg_scores, marker='o', label='Silhouette Coefficient')  

plt.title('Silhouette Coefficient for Different min_samples-DBSCAN-eps=0.4')  
plt.xlabel('Number of min_samples (min_samples)')  
plt.ylabel('Silhouette Coefficient')  
plt.legend()
plt.show()
 
plt.plot(range(2, 11), Calinski_Harabasz_scores, marker='o', label=' Calinski-Harabasz')  
plt.title('Calinski-Harabasz for Different min_samples-DBSCAN-eps=0.4')  
plt.xlabel('Number of min_samples (min_samples)')  
plt.ylabel('Calinski Harabasz')  
plt.legend()
plt.show()

  
plt.plot(range(2, 11), Davies_Bouldin_scores, marker='o', label='Davies-Bouldin Index')  
plt.title('Davies-Bouldin Index for Different min_samples-DBSCAN-eps=0.4')  
plt.xlabel('Number of min_samples (min_samples)')  
plt.ylabel('Davies-Bouldin Index')  
plt.legend()
plt.show()



# 评估指标列表  
silhouette_avg_scores = []  
  
Calinski_Harabasz_scores = []  
Davies_Bouldin_scores = []  

xindex= [0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,1.1,1.2,1.4,1.6]
for s in xindex:  
    print(s)
    dbscan = DBSCAN(eps=s, min_samples=3).fit(X) #导入DBSCAN模块进行训练,在一个邻域的半径内min_samples数的邻域eps被认为是一个簇。请记住，初始点包含在min_samples中。
    label_pred = dbscan.labels_ # labels为每个数据的簇标签,不在任何“高密度”集群中的“noisy”样本返回-1
    silhouette_avg = silhouette_score(X, dbscan.labels_)  
    print(silhouette_avg)

  
 
# 2. Calinski-Harabasz指数
   
    calinski_haraba=calinski_harabasz_score(X, dbscan.labels_)
    print(calinski_haraba)
 
    # 3. DB指数（Davies-Bouldin Index）
    davies_bouldin=davies_bouldin_score(X, dbscan.labels_)
    Davies_Bouldin_scores.append(davies_bouldin)
    Calinski_Harabasz_scores.append(calinski_haraba)
    silhouette_avg_scores.append(silhouette_avg)  
  
# 绘制图形  
plt.plot(xindex, silhouette_avg_scores, marker='o', label='Silhouette Coefficient')  

plt.title('Silhouette Coefficient for Different min_samples-DBSCAN- min_samples=3')  
plt.xlabel('eps')  
plt.ylabel('Silhouette Coefficient')  
plt.legend()
plt.show()
 
plt.plot(xindex, Calinski_Harabasz_scores, marker='o', label=' Calinski-Harabasz')  
plt.title('Calinski-Harabasz for Different min_samples-DBSCAN- min_samples=3')  
plt.xlabel('eps')  
plt.ylabel('Calinski Harabasz')  
plt.legend()
plt.show()

  
plt.plot(xindex, Davies_Bouldin_scores, marker='o', label='Davies-Bouldin Index')  
plt.title('Davies-Bouldin Index for Different min_samples-DBSCAN- min_samples=3')  
plt.xlabel('eps')  
plt.ylabel('Davies-Bouldin Index')  
plt.legend()
plt.show()

运行结果：
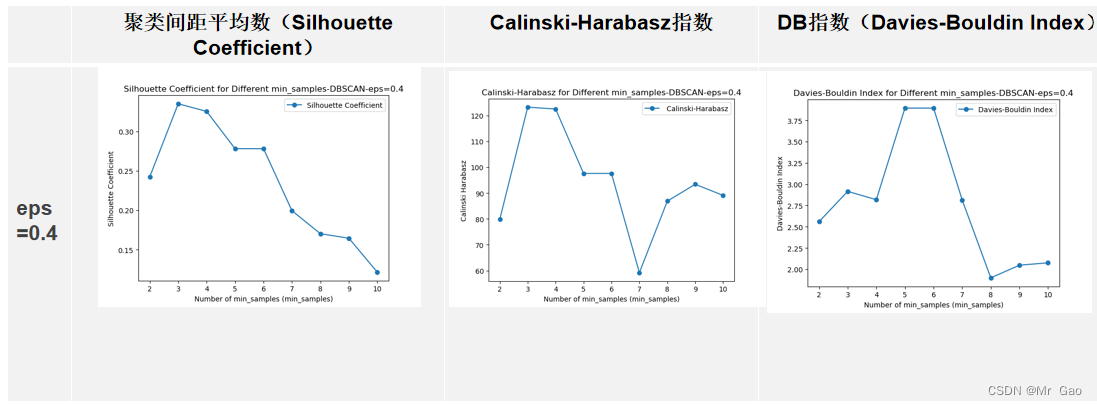在这里插入图片描述
在这里插入图片描述层次聚类：

import matplotlib.pyplot as plt # 导入matplotlib的库
import numpy as np # 导入numpy的包
from sklearn import datasets #导入数据集
from sklearn.decomposition import PCA # PCA主成分分析类
from sklearn.metrics import silhouette_score
from sklearn.metrics import calinski_harabasz_score
from sklearn.metrics import davies_bouldin_score

from sklearn.cluster import AgglomerativeClustering
iris = datasets.load_iris() #加载iris数据集
X = iris.data #加载特征数据
# Y = iris.target #加载标签数据
#绘制数据分布图
y = iris.target
X = iris.data
#X.shape
#调用PCA
pca = PCA(n_components=2) # 降到2维
pca = pca.fit(X) #拟合模型
X_dr = pca.transform(X) #获取新矩阵 （降维后的）
#X_dr



#也可以fit_transform一步到位
#X_dr = PCA(2).fit_transform(X)


#plt.figure()
#plt.scatter(X_dr[y==0, 0], X_dr[y==0, 1], c="red", label=iris.target_names[0]) 
#plt.scatter(X_dr[y==1, 0], X_dr[y==1, 1], c="black", label=iris.target_names[1])
#plt.scatter(X_dr[y==2, 0], X_dr[y==2, 1], c="orange", label=iris.target_names[2])
#plt.legend()
#plt.title('PCA of IRIS dataset')
#plt.show()


print("===K-means聚类===")
from sklearn.cluster import KMeans # 引入KMeans模块


estimator = KMeans(n_clusters=3).fit(X)  # 构造聚类器
label_pred = estimator.labels_  # 获取聚类标签

# 评估指标列表  
silhouette_avg_scores = []  
  
Calinski_Harabasz_scores = []  
Davies_Bouldin_scores = []  
# 遍历不同的n_clusters值  
for n_clusters in range(2, 11):  
    agg = AgglomerativeClustering( n_clusters=n_clusters)
    agg.fit(X)  
    labels = agg.labels_  
    silhouette_avg = silhouette_score(X, agg.labels_)  
# 2. Calinski-Harabasz指数
    calinski_haraba=calinski_harabasz_score(X, agg.labels_)
 
    # 3. DB指数（Davies-Bouldin Index）
    davies_bouldin=davies_bouldin_score(X, agg.labels_)
    Davies_Bouldin_scores.append(davies_bouldin)
    Calinski_Harabasz_scores.append(calinski_haraba)
    silhouette_avg_scores.append(silhouette_avg)  
  
# 绘制图形  
plt.plot(range(2, 11), silhouette_avg_scores, marker='o', label='Silhouette Coefficient')  

plt.title('Silhouette Coefficient for Different n_clusters-AgglomerativeClustering')  
plt.xlabel('Number of clusters (n_clusters)')  
plt.ylabel('Silhouette Coefficient')  
plt.legend()
plt.show()
 
plt.plot(range(2, 11), Calinski_Harabasz_scores, marker='o', label=' Calinski-Harabasz')  
plt.title(' Calinski-Harabaszfor Different n_clusters-AgglomerativeClustering')  
plt.xlabel('Number of clusters (n_clusters)')  
plt.ylabel('Calinski Harabasz')  
plt.legend()
plt.show()

  
plt.plot(range(2, 11), Davies_Bouldin_scores, marker='o', label='Davies-Bouldin Index')  
plt.title('Davies-Bouldin Index for Different n_clusters-AgglomerativeClustering')  
plt.xlabel('Number of clusters (n_clusters)')  
plt.ylabel('Davies-Bouldin Index')  
plt.legend()
plt.show()

运行结果：
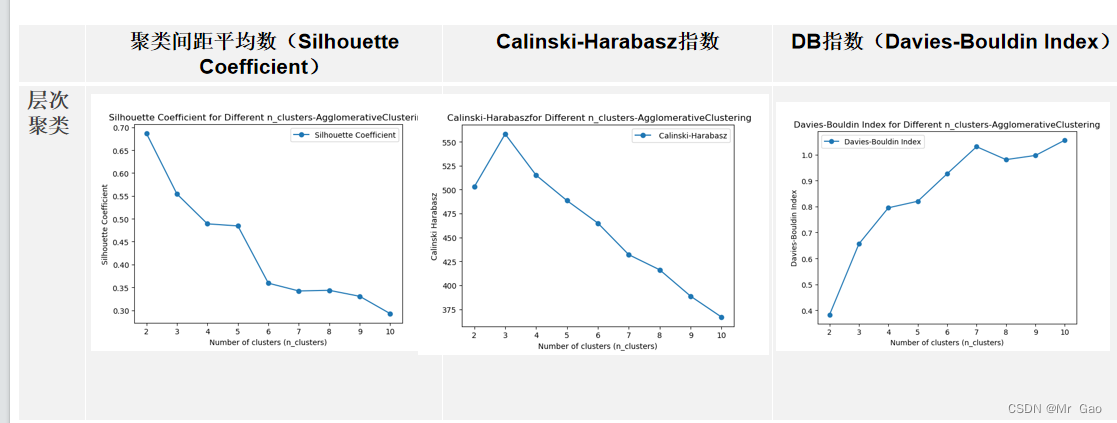
在这里插入图片描述
FCM算法：

代码：

import matplotlib.pyplot as plt # 导入matplotlib的库
import numpy as np # 导入numpy的包
from sklearn import datasets #导入数据集
from sklearn.decomposition import PCA # PCA主成分分析类
from sklearn.metrics import silhouette_score
from sklearn.metrics import calinski_harabasz_score
from sklearn.metrics import davies_bouldin_score
from sklearn.cluster import FeatureAgglomeration
from sklearn.cluster import AgglomerativeClustering
iris = datasets.load_iris() #加载iris数据集
X = iris.data #加载特征数据
# Y = iris.target #加载标签数据
#绘制数据分布图
y = iris.target
X = iris.data
#X.shape
#调用PCA
pca = PCA(n_components=2) # 降到2维
pca = pca.fit(X) #拟合模型
X_dr = pca.transform(X) #获取新矩阵 （降维后的）
#X_dr



#也可以fit_transform一步到位
#X_dr = PCA(2).fit_transform(X)


#plt.figure()
#plt.scatter(X_dr[y==0, 0], X_dr[y==0, 1], c="red", label=iris.target_names[0]) 
#plt.scatter(X_dr[y==1, 0], X_dr[y==1, 1], c="black", label=iris.target_names[1])
#plt.scatter(X_dr[y==2, 0], X_dr[y==2, 1], c="orange", label=iris.target_names[2])
#plt.legend()
#plt.title('PCA of IRIS dataset')
#plt.show()


print("===K-means聚类===")
from sklearn.cluster import KMeans # 引入KMeans模块
def FCM(X, c_clusters=3, m=2, eps=10):
    membership_mat = np.random.random((len(X), c_clusters))   # 生成随机二维数组shape(150,3)，随机初始化隶属矩阵
    # 这一步的操作是为了使Xi的隶属度总和为1
    membership_mat = np.divide(membership_mat, np.sum(membership_mat, axis=1)[:, np.newaxis])

    while True:
        working_membership_mat = membership_mat ** m   # shape->(150,3)
        # 根据公式计算聚类中心点Centroids.shape->(3,4)
        Centroids = np.divide(np.dot(working_membership_mat.T, X), np.sum(working_membership_mat.T, axis=1)[:, np.newaxis])

        # 该矩阵保存所有实点到每个聚类中心的欧式距离
        n_c_distance_mat = np.zeros((len(X), c_clusters)) # shape->(150,3)
        for i, x in enumerate(X):
            for j, c in enumerate(Centroids):
                n_c_distance_mat[i][j] = np.linalg.norm(x-c, 2)   # 计算l2范数(欧氏距离)

        new_membership_mat = np.zeros((len(X), c_clusters))

        # 根据公式计算模糊矩阵U
        for i, x in enumerate(X):
            for j, c in enumerate(Centroids):
                new_membership_mat[i][j] = 1. / np.sum((n_c_distance_mat[i][j] / n_c_distance_mat[i]) ** (2 / (m-1)))
        if np.sum(abs(new_membership_mat - membership_mat)) < eps:
            break
        membership_mat = new_membership_mat
    return np.argmax(new_membership_mat, axis=1)



# 评估指标列表  
silhouette_avg_scores = []  
  
Calinski_Harabasz_scores = []  
Davies_Bouldin_scores = []  
# 遍历不同的n_clusters值  
for n_clusters in range(2, 11):  
    print(n_clusters)
    fcm =FCM(X, c_clusters=n_clusters)
  
    print(len(fcm ))
    silhouette_avg = silhouette_score(X, fcm)  
    print(silhouette_avg)
# 2. Calinski-Harabasz指数
    calinski_haraba=calinski_harabasz_score(X, fcm)
    print(calinski_haraba)
 
    # 3. DB指数（Davies-Bouldin Index）
    davies_bouldin=davies_bouldin_score(X,fcm)
    Davies_Bouldin_scores.append(davies_bouldin)
    Calinski_Harabasz_scores.append(calinski_haraba)
    silhouette_avg_scores.append(silhouette_avg)  
  
# 绘制图形  
plt.plot(range(2, 11), silhouette_avg_scores, marker='o', label='Silhouette Coefficient')  

plt.title('Silhouette Coefficient for Different n_clusters-FCM')  
plt.xlabel('Number of clusters (n_clusters)')  
plt.ylabel('Silhouette Coefficient')  
plt.legend()
plt.show()
 
plt.plot(range(2, 11), Calinski_Harabasz_scores, marker='o', label=' Calinski-Harabasz')  
plt.title(' Calinski-Harabaszfor Different n_clusters-FCM')  
plt.xlabel('Number of clusters (n_clusters)')  
plt.ylabel('Calinski Harabasz')  
plt.legend()
plt.show()

  
plt.plot(range(2, 11), Davies_Bouldin_scores, marker='o', label='Davies-Bouldin Index')  
plt.title('Davies-Bouldin Index for Different n_clusters-FCM')  
plt.xlabel('Number of clusters (n_clusters)')  
plt.ylabel('Davies-Bouldin Index')  
plt.legend()
plt.show()

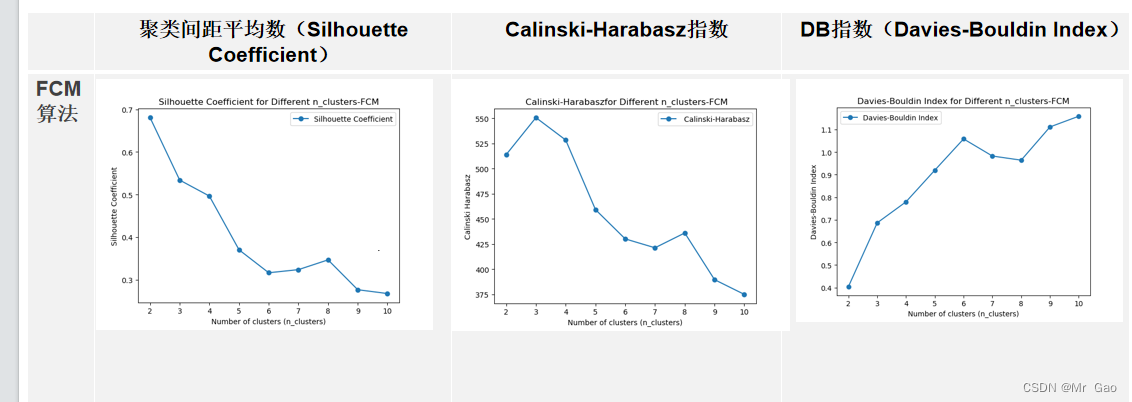
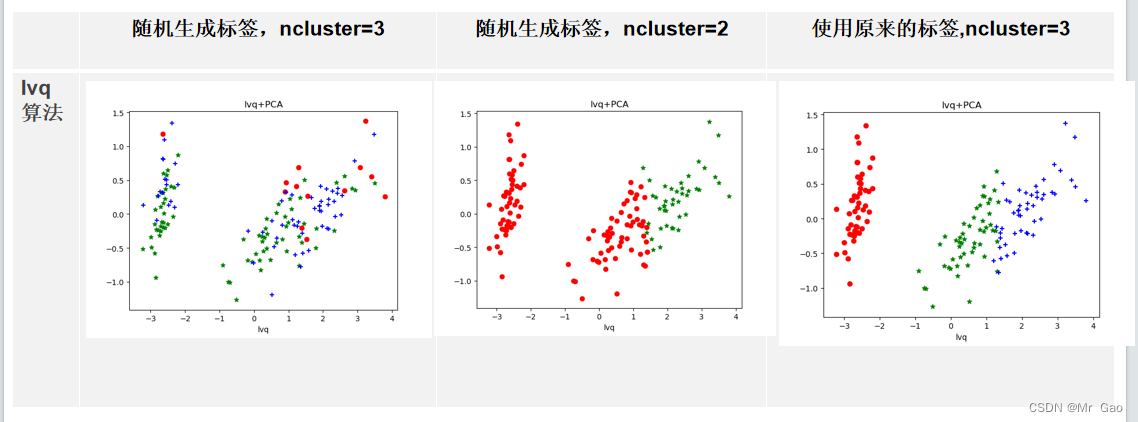
在这里插入图片描述
lvp算法：

import matplotlib.pyplot as plt # 导入matplotlib的库
import numpy as np # 导入numpy的包
from sklearn import datasets #导入数据集
from sklearn.decomposition import PCA # PCA主成分分析类
from sklearn.metrics import silhouette_score
from sklearn.metrics import calinski_harabasz_score
from sklearn.metrics import davies_bouldin_score
from sklearn.cluster import FeatureAgglomeration
from sklearn.cluster import AgglomerativeClustering

 
# 使用LVQ进行聚类
from sklearn_lvq import GlvqModel
 


iris = datasets.load_iris() #加载iris数据集
X = iris.data #加载特征数据
# Y = iris.target #加载标签数据
#绘制数据分布图
y = iris.target
X = iris.data
#X.shape
#调用PCA
pca = PCA(n_components=2) # 降到2维
pca = pca.fit(X) #拟合模型
X_dr = pca.transform(X) #获取新矩阵 （降维后的）
#X_dr



#也可以fit_transform一步到位
#X_dr = PCA(2).fit_transform(X)


#plt.figure()
#plt.scatter(X_dr[y==0, 0], X_dr[y==0, 1], c="red", label=iris.target_names[0]) 
#plt.scatter(X_dr[y==1, 0], X_dr[y==1, 1], c="black", label=iris.target_names[1])
#plt.scatter(X_dr[y==2, 0], X_dr[y==2, 1], c="orange", label=iris.target_names[2])
#plt.legend()
#plt.title('PCA of IRIS dataset')
#plt.show()
def FCM(X, c_clusters=3, m=2, eps=10):
    membership_mat = np.random.random((len(X), c_clusters))   # 生成随机二维数组shape(150,3)，随机初始化隶属矩阵
    # 这一步的操作是为了使Xi的隶属度总和为1
    membership_mat = np.divide(membership_mat, np.sum(membership_mat, axis=1)[:, np.newaxis])

    while True:
        working_membership_mat = membership_mat ** m   # shape->(150,3)
        # 根据公式计算聚类中心点Centroids.shape->(3,4)
        Centroids = np.divide(np.dot(working_membership_mat.T, X), np.sum(working_membership_mat.T, axis=1)[:, np.newaxis])

        # 该矩阵保存所有实点到每个聚类中心的欧式距离
        n_c_distance_mat = np.zeros((len(X), c_clusters)) # shape->(150,3)
        for i, x in enumerate(X):
            for j, c in enumerate(Centroids):
                n_c_distance_mat[i][j] = np.linalg.norm(x-c, 2)   # 计算l2范数(欧氏距离)

        new_membership_mat = np.zeros((len(X), c_clusters))

        # 根据公式计算模糊矩阵U
        for i, x in enumerate(X):
            for j, c in enumerate(Centroids):
                new_membership_mat[i][j] = 1. / np.sum((n_c_distance_mat[i][j] / n_c_distance_mat[i]) ** (2 / (m-1)))
        if np.sum(abs(new_membership_mat - membership_mat)) < eps:
            break
        membership_mat = new_membership_mat
    return np.argmax(new_membership_mat, axis=1)



# 评估指标列表  
silhouette_avg_scores = []  
  
Calinski_Harabasz_scores = []  
Davies_Bouldin_scores = []  
from sklearn.datasets import make_blobs

# 遍历不同的n_clusters值  
for n_clusters in range(2, 11):  
    print(n_clusters)
    zX, y_true = make_blobs(n_samples=150, centers=n_clusters, cluster_std=0.6, random_state=0)
    lvq = GlvqModel()
    lvq.fit(X, y_true)
 
    # 可视化聚类结果
    fcm = lvq.predict(X)
   
  
    print(len(fcm ))
    silhouette_avg = silhouette_score(X, fcm)  
    print(silhouette_avg)
# 2. Calinski-Harabasz指数
    calinski_haraba=calinski_harabasz_score(X, fcm)
    print(calinski_haraba)
 
    # 3. DB指数（Davies-Bouldin Index）
    davies_bouldin=davies_bouldin_score(X,fcm)
    Davies_Bouldin_scores.append(davies_bouldin)
    Calinski_Harabasz_scores.append(calinski_haraba)
    silhouette_avg_scores.append(silhouette_avg)  
  
# 绘制图形  
plt.plot(range(2, 11), silhouette_avg_scores, marker='o', label='Silhouette Coefficient')  

plt.title('Silhouette Coefficient for Different n_clusters--lvp')  
plt.xlabel('Number of clusters (n_clusters)')  
plt.ylabel('Silhouette Coefficient')  
plt.legend()
plt.show()
 
plt.plot(range(2, 11), Calinski_Harabasz_scores, marker='o', label=' Calinski-Harabasz')  
plt.title(' Calinski-Harabaszfor Different n_clusters--lvp')  
plt.xlabel('Number of clusters (n_clusters)')  
plt.ylabel('Calinski Harabasz')  
plt.legend()
plt.show()

  
plt.plot(range(2, 11), Davies_Bouldin_scores, marker='o', label='Davies-Bouldin Index')  
plt.title('Davies-Bouldin Index for Different n_clusters-lvp')  
plt.xlabel('Number of clusters (n_clusters)')  
plt.ylabel('Davies-Bouldin Index')  
plt.legend()
plt.show()

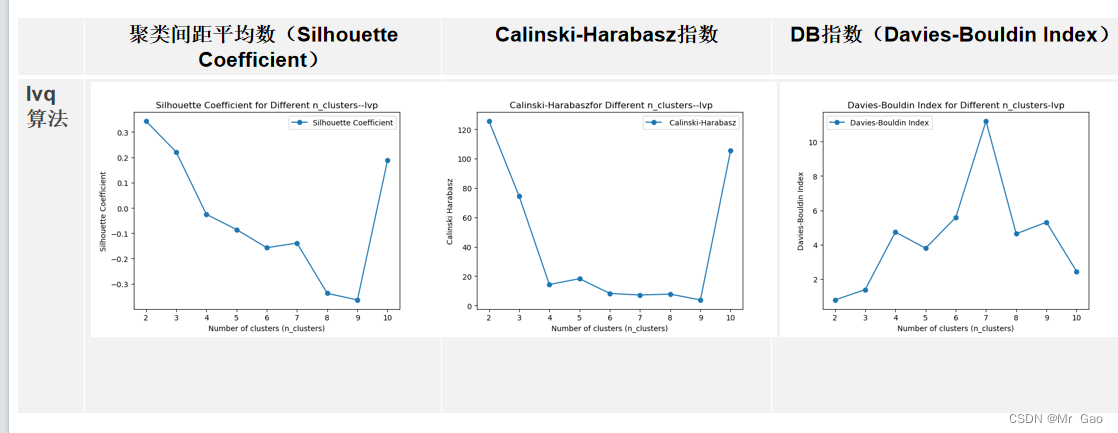
在这里插入图片描述
最后我们还做了一个所有算法最优参数汇总的代码：

import matplotlib.pyplot as plt # 导入matplotlib的库
import numpy as np # 导入numpy的包
from sklearn import datasets #导入数据集
from sklearn.decomposition import PCA # PCA主成分分析类
iris = datasets.load_iris() #加载iris数据集
X = iris.data #加载特征数据
# Y = iris.target #加载标签数据
#绘制数据分布图
y = iris.target
X = iris.data
#X.shape
#调用PCA
pca = PCA(n_components=2) # 降到2维
pca = pca.fit(X) #拟合模型
X_dr = pca.transform(X) #获取新矩阵 （降维后的）
#X_dr



#也可以fit_transform一步到位
X_dr = PCA(2).fit_transform(X)


plt.figure()
plt.scatter(X_dr[y==0, 0], X_dr[y==0, 1], c="red", label=iris.target_names[0]) 
plt.scatter(X_dr[y==1, 0], X_dr[y==1, 1], c="black", label=iris.target_names[1])
plt.scatter(X_dr[y==2, 0], X_dr[y==2, 1], c="orange", label=iris.target_names[2])
plt.legend()
plt.title('PCA of IRIS dataset')
plt.show()


print("===K-means聚类===")
from sklearn.cluster import KMeans # 引入KMeans模块
estimator = KMeans(n_clusters=3).fit(X)  # 构造聚类器
label_pred = estimator.labels_  # 获取聚类标签
#绘制k-means结果
x0 = X_dr[label_pred == 0]# 获取聚类标签等于0的话，则赋值给x0
x1 = X_dr[label_pred == 1]# 获取聚类标签等于1的话，则赋值给x1
x2 = X_dr[label_pred == 2]# 获取聚类标签等于2的话，则赋值给x2
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label 0')#画label 0的散点图
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label 1')#画label 1的散点图
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label 2')#画label 2的散点图
plt.xlabel('K-means')# 设置X轴的标签为K-means
# plt.legend(loc=2)# 设置图标在左上角
plt.title("kmeans+PCA")
plt.show()


x0 = X[label_pred == 0]# 获取聚类标签等于0的话，则赋值给x0
x1 = X[label_pred == 1]# 获取聚类标签等于1的话，则赋值给x1
x2 = X[label_pred == 2]# 获取聚类标签等于2的话，则赋值给x2
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label 0')#画la

plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label 1')#画label 1的散点图
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label 2')#画label 2的散点图
plt.xlabel('K-means')# 设置X轴的标签为K-means
# plt.legend(loc=2)# 设置图标在左上角
plt.title("kmeans-features[0:2]")
plt.show()


#密度聚类之DBSCAN算法
print("===DBSCAN聚类===")
from sklearn.cluster import DBSCAN # 引入DBSCAN模块
dbscan = DBSCAN(eps=1.0, min_samples=3).fit(X) #导入DBSCAN模块进行训练,在一个邻域的半径内min_samples数的邻域eps被认为是一个簇。请记住，初始点包含在min_samples中。
label_pred = dbscan.labels_ # labels为每个数据的簇标签,不在任何“高密度”集群中的“noisy”样本返回-1

x0 = X[label_pred == 0] # 获取聚类标签等于0的话，则赋值给x0
x1 = X[label_pred == 1] # 获取聚类标签等于1的话，则赋值给x1
x2 = X[label_pred == 2] # 获取聚类标签等于2的话，则赋值给x2
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0') # 画label 0的散点图
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1') # 画label 1的散点图
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2') # 画label 2的散点图
plt.xlabel('DBSCAN')# 设置X轴的标签为DBSCAN
plt.legend(loc=2)# 设置图标在左上角
plt.title("DBSCAN-features[0:2]")
plt.show()



x0 = X_dr[label_pred == 0]# 获取聚类标签等于0的话，则赋值给x0
x1 = X_dr[label_pred == 1]# 获取聚类标签等于1的话，则赋值给x1
x2 = X_dr[label_pred == 2]# 获取聚类标签等于2的话，则赋值给x2
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label 0')#画label 0的散点图
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label 1')#画label 1的散点图
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label 2')#画label 2的散点图
plt.xlabel('DBSCAN')# 设置X轴的标签为K-means
# plt.legend(loc=2)# 设置图标在左上角
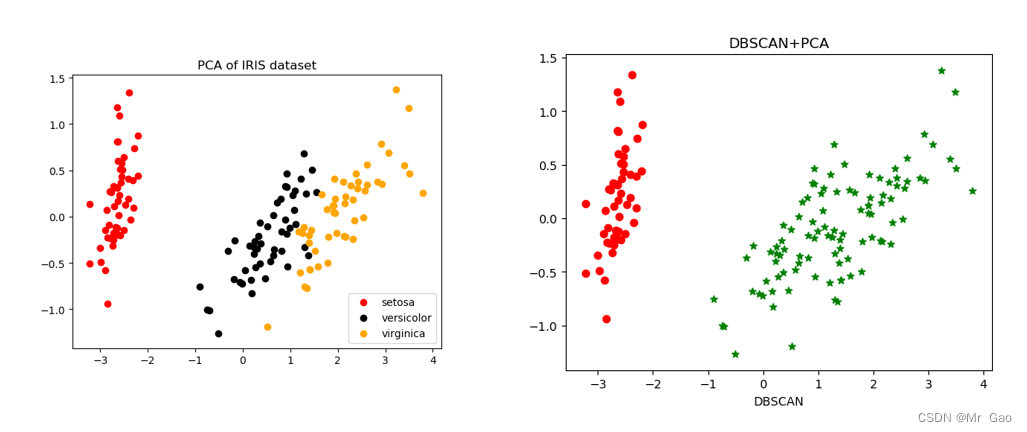
plt.title("DBSCAN+PCA")
plt.show()
from sklearn_lvq import GlvqModel

import numpy as np
from matplotlib import pyplot as plt
from scipy.cluster.hierarchy import dendrogram
from scipy.cluster.hierarchy import linkage, dendrogram
def getLinkageMat(model):
    children = model.children_
    cs = np.zeros(len(children))
    N = len(model.labels_)
    for i,child in enumerate(children):
        count = 0
        for idx in child:
            count += 1 if idx < N else cs[idx - N]
        cs[i] = count
    return np.column_stack([children, model.distances_, cs])

from sklearn.cluster import AgglomerativeClustering
from sklearn.datasets import make_blobs

model = AgglomerativeClustering( n_clusters=3)

model = model.fit(X)

label_pred = model.labels_ # labels为每个数据的簇标签,不在任何“高密度”集群中的“noisy”样本返回-1

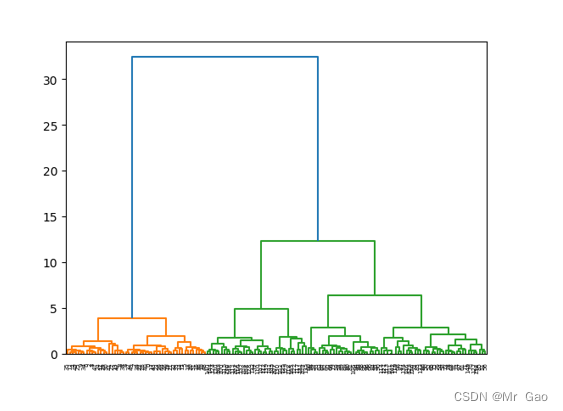
Z = linkage(X, method='ward', metric='euclidean')
p = dendrogram(Z, 0)
plt.show()



x0 = X_dr[label_pred == 0]# 获取聚类标签等于0的话，则赋值给x0
x1 = X_dr[label_pred == 1]# 获取聚类标签等于1的话，则赋值给x1
x2 = X_dr[label_pred == 2]# 获取聚类标签等于2的话，则赋值给x2
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label 0')#画label 0的散点图
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label 1')#画label 1的散点图
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label 2')#画label 2的散点图
plt.xlabel('AgglomerativeClustering')# 设置X轴的标签为K-means
# plt.legend(loc=2)# 设置图标在左上角
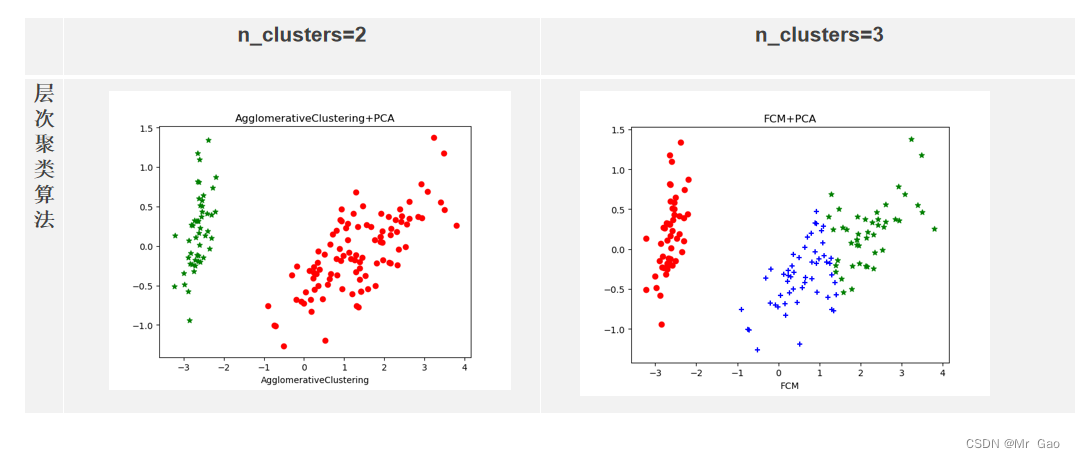
plt.title("AgglomerativeClustering+PCA")
plt.show()

def FCM(X, c_clusters=3, m=2, eps=10):
    membership_mat = np.random.random((len(X), c_clusters))   # 生成随机二维数组shape(150,3)，随机初始化隶属矩阵
    # 这一步的操作是为了使Xi的隶属度总和为1
    membership_mat = np.divide(membership_mat, np.sum(membership_mat, axis=1)[:, np.newaxis])

    while True:
        working_membership_mat = membership_mat ** m   # shape->(150,3)
        # 根据公式计算聚类中心点Centroids.shape->(3,4)
        Centroids = np.divide(np.dot(working_membership_mat.T, X), np.sum(working_membership_mat.T, axis=1)[:, np.newaxis])

        # 该矩阵保存所有实点到每个聚类中心的欧式距离
        n_c_distance_mat = np.zeros((len(X), c_clusters)) # shape->(150,3)
        for i, x in enumerate(X):
            for j, c in enumerate(Centroids):
                n_c_distance_mat[i][j] = np.linalg.norm(x-c, 2)   # 计算l2范数(欧氏距离)

        new_membership_mat = np.zeros((len(X), c_clusters))

        # 根据公式计算模糊矩阵U
        for i, x in enumerate(X):
            for j, c in enumerate(Centroids):
                new_membership_mat[i][j] = 1. / np.sum((n_c_distance_mat[i][j] / n_c_distance_mat[i]) ** (2 / (m-1)))
        if np.sum(abs(new_membership_mat - membership_mat)) < eps:
            break
        membership_mat = new_membership_mat
    return np.argmax(new_membership_mat, axis=1)

fcm =FCM(X, c_clusters=3)


x0 = X_dr[fcm == 0]# 获取聚类标签等于0的话，则赋值给x0
x1 = X_dr[fcm == 1]# 获取聚类标签等于1的话，则赋值给x1
x2 = X_dr[fcm == 2]# 获取聚类标签等于2的话，则赋值给x2
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label 0')#画label 0的散点图
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label 1')#画label 1的散点图
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label 2')#画label 2的散点图
plt.xlabel('FCM')# 设置X轴的标签为K-means
# plt.legend(loc=2)# 设置图标在左上角
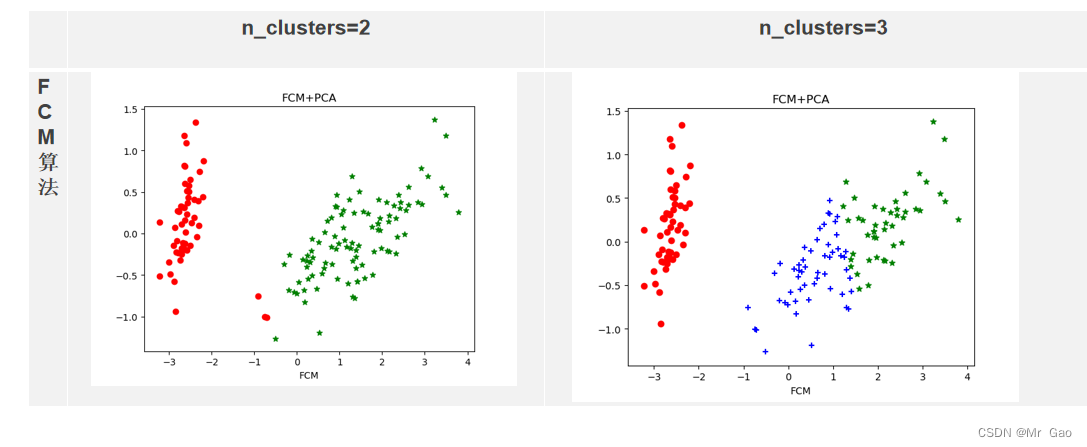
plt.title("FCM+PCA")
plt.show()

zX, y_true = make_blobs(n_samples=150, centers=2, cluster_std=0.6, random_state=0)
lvq = GlvqModel()
lvq.fit(X, y)
 
    # 可视化聚类结果
lvqp = lvq.predict(X)




x0 = X_dr[lvqp == 0]# 获取聚类标签等于0的话，则赋值给x0
x1 = X_dr[lvqp == 1]# 获取聚类标签等于1的话，则赋值给x1
x2 = X_dr[lvqp == 2]# 获取聚类标签等于2的话，则赋值给x2
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label 0')#画label 0的散点图
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label 1')#画label 1的散点图
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label 2')#画label 2的散点图
plt.xlabel('lvq')# 设置X轴的标签为K-means
# plt.legend(loc=2)# 设置图标在左上角
plt.title("lvq+PCA")
plt.show()

运行结果：
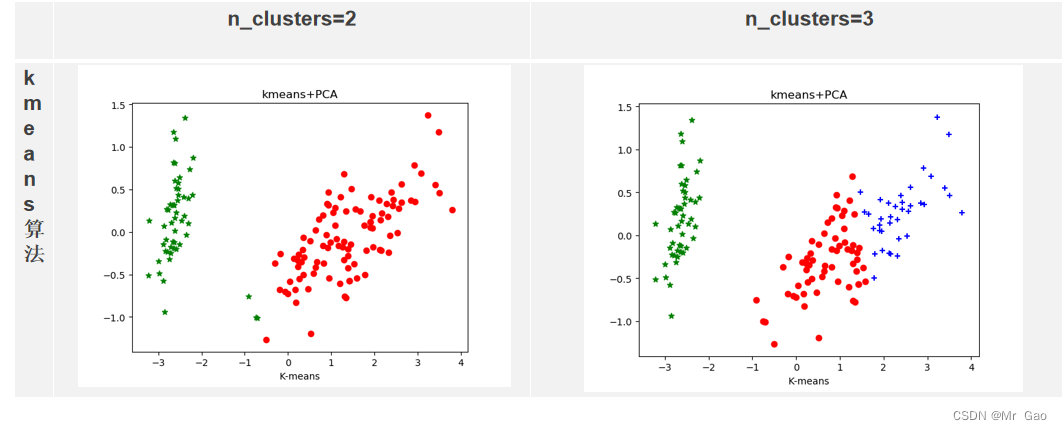
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1647077.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

JavaScript之数据类型（2）——复杂类型(object)

JavaScript之数据类型（2）——复杂类型(object)

object的介绍&#xff1a; 我对于object的理解是和C/C中的结构体一样&#xff0c;是一个自定义的数据类型&#xff0c;我们可以通过多个简单的数据类型来定义一个便于我们使用的新的数据类型。 在网上某佬对于其解释如下&#xff1a; Object类型&#xff0c;我们也称为一个对象…
阅读更多...
ubuntu 安装单节点HBase

ubuntu 安装单节点HBase

下载HBase mkdir -p /home/ellis/HBase/ cd /home/ellis/HBase/ wget https://downloads.apache.org/hbase/2.5.8/hbase-2.5.8-bin.tar.gz tar -xvf hbase-2.5.8-bin.tar.gz安装java jdk sudo apt install openjdk-11-jdksudo vim /etc/profileexport JAVA_HOME/usr/lib/jvm/…
阅读更多...
设计模式之传输对象模式

设计模式之传输对象模式

在编程江湖里&#xff0c;有一种模式&#xff0c;它如同数据的“特快专递”&#xff0c;穿梭于系统间&#xff0c;保证信息的快速准确送达&#xff0c;它就是——传输对象模式&#xff08;Data Transfer Object, DTO&#xff09;。这不仅仅是数据的搬运工&#xff0c;更是提升系…
阅读更多...
bfs之走迷宫

bfs之走迷宫

文章目录 走迷宫广度优先遍历代码Java代码打印路径 走迷宫 给定一个 nm 的二维整数数组&#xff0c;用来表示一个迷宫&#xff0c;数组中只包含 0或 1&#xff0c;其中 0表示可以走的路&#xff0c;1表示不可通过的墙壁。 最初&#xff0c;有一个人位于左上角 (1,1) 处&#…
阅读更多...
MATLAB绘制蒸汽压力和温度曲线

MATLAB绘制蒸汽压力和温度曲线

蒸汽压力与温度之间的具体关系公式一般采用安托因方程&#xff08;Antoine Equation&#xff09;&#xff0c;用于描述纯物质的蒸汽压与温度之间的关系。安托因方程的一般形式如下&#xff1a; [\log_{10} P A - \frac{B}{C T}] 其中&#xff0c; (P) 是蒸汽压&#xff08…
阅读更多...
syncGradle项目时报错Unknown Kotlin JVM target: 22

syncGradle项目时报错Unknown Kotlin JVM target: 22

解决方案1 定位到build.gradle.kts的出问题行&#xff0c;将其注释掉然后把sourceCompatibility行也注释掉重新sync. 这样会自动使用默认兼容的版本 你也可以根据文档手动解决兼容问题2 Configure a Gradle project | Kotlin Documentation (kotlinlang.org) ↩︎ Compatibil…
阅读更多...
[VulnHub靶机渗透] Hackademic: RTB1

[VulnHub靶机渗透] Hackademic: RTB1

&#x1f36c; 博主介绍&#x1f468;‍&#x1f393; 博主介绍&#xff1a;大家好&#xff0c;我是 hacker-routing &#xff0c;很高兴认识大家~ ✨主攻领域&#xff1a;【渗透领域】【应急响应】 【Java、PHP】 【VulnHub靶场复现】【面试分析】 &#x1f389;点赞➕评论➕收…
阅读更多...
一、Vagrant搭建相关环境

一、Vagrant搭建相关环境

目录 一、创建Vagrant相关环境1.下载安装VirtualBox2.在BlOS中设置CPU虚拟化3.使用Vagrant新建linux虚拟机3.1下载Vagrant3.2Vagrant官方镜像仓库3.3使用Vagrant初始化一个centos7的虚拟机 4.设置固定ip地址 二、安装docker1.按照docker 三、docker安装一些中间件1.mysql安装2.…
阅读更多...
Elasticsearch：理解人工智能相似性搜索

Elasticsearch：理解人工智能相似性搜索

理解相似性搜索&#xff08;也称为语义搜索&#xff09;的指南&#xff0c;这是人工智能最新阶段的关键发现之一。 最新阶段人工智能的关键发现之一是根据相似性搜索和查找文档的能力。相似性搜索是一种比较信息的方法&#xff0c;其基于含义而非关键字。 相似性搜索也被称为语…
阅读更多...
【隧道篇 / WAN优化】(7.4) ❀ 01. 启动WAN优化 ❀ FortiGate 防火墙

【隧道篇 / WAN优化】(7.4) ❀ 01. 启动WAN优化 ❀ FortiGate 防火墙

【简介】几乎所有的人都知道&#xff0c;防火墙自带的硬盘是用来保存日志&#xff0c;以方便在出现问题时能找到原因。但是很少的人知道&#xff0c;防火墙自带的硬盘其实还有另一个功能&#xff0c;那就是用于WAN优化。 防火墙自带的硬盘 在FortiGate防火墙A、B、C、D系列&…
阅读更多...
MWeb Pro for Mac：功能强大的Markdown博客编辑器

MWeb Pro for Mac：功能强大的Markdown博客编辑器

MWeb Pro for Mac是一款功能强大的Markdown博客编辑器&#xff0c;专为Mac用户设计&#xff0c;提供了一站式的博客写作和发布体验。这款软件不仅支持Markdown语法&#xff0c;还提供了丰富的编辑和排版功能&#xff0c;让用户能够轻松创建出精美的博客内容。 MWeb Pro的即时预…
阅读更多...
每日一题4：Pandas创建新列

每日一题4：Pandas创建新列

一、每日一题 一家公司计划为员工提供奖金。 编写一个解决方案&#xff0c;创建一个名为 bonus 的新列&#xff0c;其中包含 salary 值的 两倍。 返回结果格式如下示例所示。 解答&#xff1a; import pandas as pddef createBonusColumn(employees: pd.DataFrame) -> pd.D…
阅读更多...
Redis高级（Redis持久化，Redis主从模式，Redis哨兵模式，Redis分片集群）

Redis高级（Redis持久化，Redis主从模式，Redis哨兵模式，Redis分片集群）

目录 一、单机Redis 1. 问题说明 2. 安装Redis 1 解压安装Redis【备用】 2 配置Redis 3 启动Redis 3. 小结 二、Redis持久化 1. 持久化机制介绍 2. RDB模式 3. AOF模式 4. RDB和AOF对比 5. 小结 三、Redis主从模式 1. 介绍 2. 搭建Redis主从架构【备用】 3. 主…
阅读更多...
微服务领域的寻路者 —— Eureka深度探索与实战秘籍

微服务领域的寻路者 —— Eureka深度探索与实战秘籍

文章目录 一、引言定义目标一个接地气的例子引言小结 二、Eureka架构2.1 Eureka Server一个有趣的例子2.2 Eureka Client一段简单的代码示例架构小结 三、工作流程1. 服务注册2. 心跳检测3. 服务发现4. 健康检查与失效剔除工作流程小结 四、核心机制4.1 服务注册与续约4.2 服务…
阅读更多...
2024年03月 Scratch 图形化（三级）真题解析#中国电子学会#全国青少年软件编程等级考试

2024年03月 Scratch 图形化（三级）真题解析#中国电子学会#全国青少年软件编程等级考试

Scratch图形化等级考试（1~4级）全部真题・点这里 一、单选题（共18题，共50分） 第1题 运行程序后，角色一定不会说出的数字是？（ ） A：2 B：4 C：6 D：8 答案：A 程序中随机数的取值最小为 2，最大为 20 ，那么随机数加上 2 之后的结果的最小值为 4 ，最大值为 22 。所…
阅读更多...
设备树与/sys/bus/platform/devices与/sys/devices目录关系

设备树与/sys/bus/platform/devices与/sys/devices目录关系

设备树与sys/bus/platform/devices sysfs文件系统中/sys/bus/platform/devices下的设备是由设备树生成&#xff0c; 根节点下有compatible的子节点都会在/bus/platform/devices生成节点 总线 I2C、SPI 等控制器会在/bus/platform/devices生成节点 总线 I2C、SPI 节点下的子节点…
阅读更多...
为什么电子商务安全是速度和保护之间的平衡行为

为什么电子商务安全是速度和保护之间的平衡行为

微信搜索关注公众号网络研究观&#xff0c;获取更多信息。 电子商务世界是一把双刃剑。虽然它为企业和消费者提供了便利和可访问性&#xff0c;但它也为网络犯罪分子提供了诱人的目标。在这个不断变化的环境中&#xff0c;优先考虑安全不再是一种选择&#xff1b;而是一种选择&…
阅读更多...
Reactor Netty TCP 服务器端-响应式编程-011

Reactor Netty TCP 服务器端-响应式编程-011

🤗 ApiHug {Postman|Swagger|Api...} = 快↑ 准√ 省↓ GitHub - apihug/apihug.com: All abou the Apihug apihug.com: 有爱，有温度，有质量，有信任ApiHug - API design Copilot - IntelliJ IDEs Plugin | Marketplace The Next Generation API Development Platform…
阅读更多...
【LeetCode】环形队列实现

【LeetCode】环形队列实现

目录 前言1. 环形队列概念2. 循环队列实现设计3. 功能实现3.1 定义3.2 初始化3.3 判断队列是否为空3.4 判断队列是否为满3.5 入栈3.6 出栈3.7 获取队头数据3.8 获取队尾数据3.9 销毁 4. 总结5. 完整通过代码 前言 之前我们学习环形链表相关问题&#xff0c;现在我们来看看环形…
阅读更多...
opencv_21_直方图均衡化

opencv_21_直方图均衡化

1&#xff09;void histogram_eq_demo(Mat& image); 2&#xff09;void ColorInvert::histogram_eq_demo(Mat& image) { Mat gray; cvtColor(image, gray, COLOR_BGR2GRAY); imshow("灰度图像", gray); Mat dst; equalizeHist(gray, ds…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023