文章目录
- 走迷宫
- 广度优先遍历
- 代码
- Java代码
- 打印路径
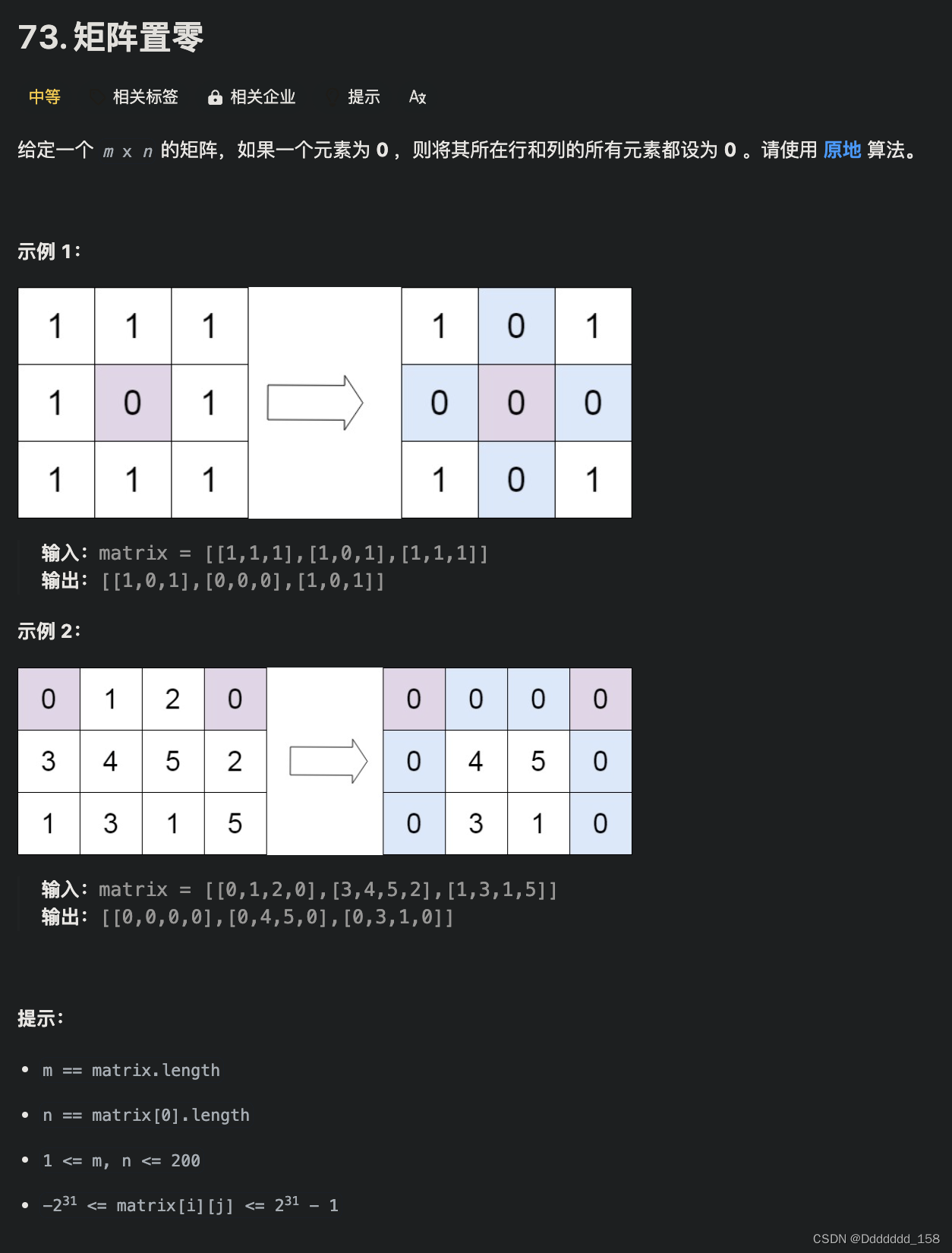
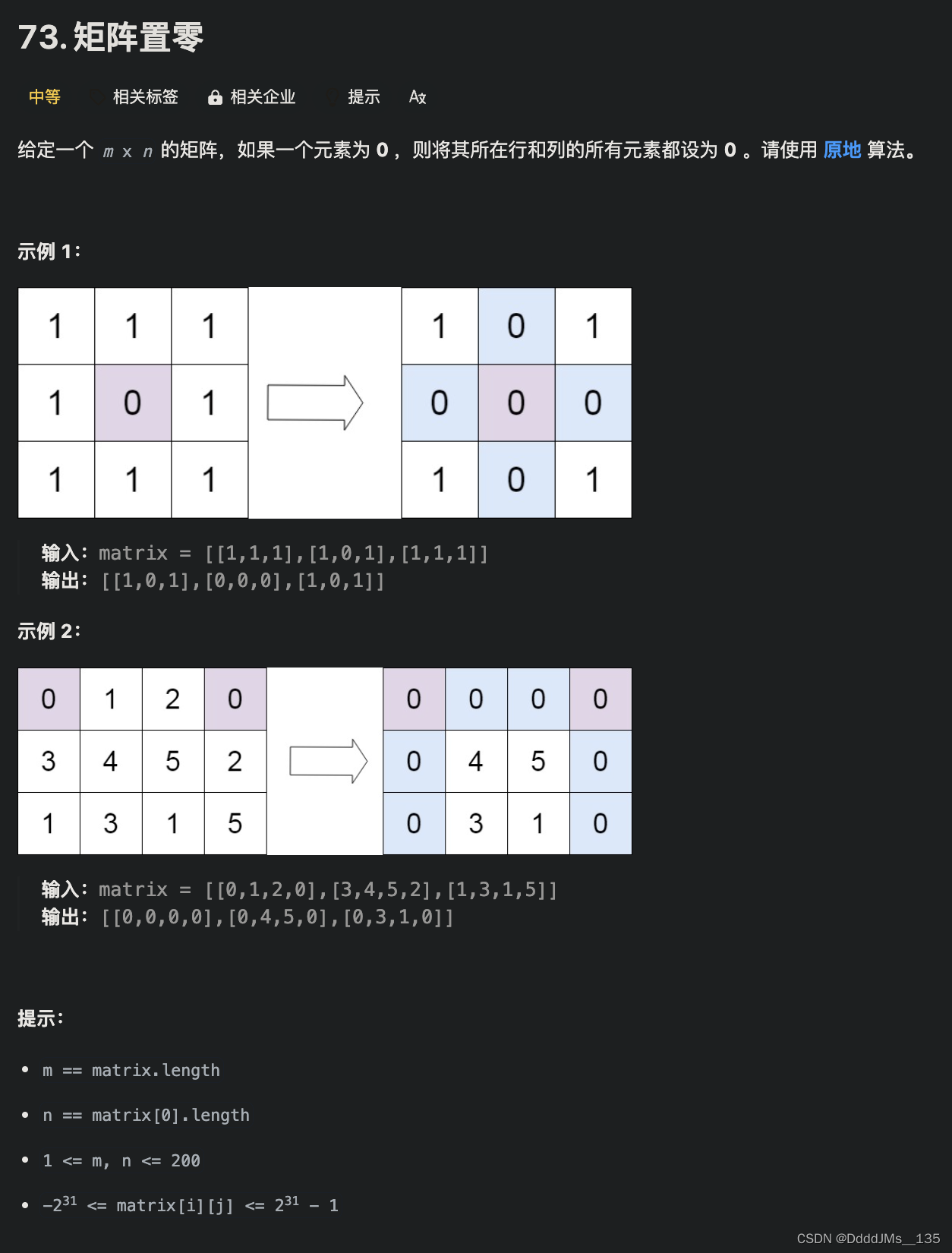
走迷宫
给定一个 n×m
的二维整数数组,用来表示一个迷宫,数组中只包含 0或 1,其中 0表示可以走的路,1表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m)处,至少需要移动多少次。
数据保证 (1,1)处和 (n,m) 处的数字为 0,且一定至少存在一条通路。
输入格式
第一行包含两个整数 n和 m。
接下来 n行,每行包含 m个整数(0或 1),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1 ≤ n,m ≤ 100
输入样例:
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样例:
8
广度优先遍历
思路:从起点开始,往前走第一步,记录下所有第一步能走到的点,然后从所第一步能走到的点开始,往前走第二步,记录下所有第二步能走到的点,重复下去,直到走到终点。输出步数即可。
这就是广度优先遍历的思路。
实现方式:广度优先遍历
-
用 g 存储地图,f存储起点到其他各个点的距离。
-
从起点开始广度优先遍历地图。
-
当地图遍历完,就求出了起点到各个点的距离,输出f[n][m]即可。

-
void bfs(int a, int b): 广度优遍历函数。输入的是起点坐标。
-
queue q;:用来存储每一步走到的点。
-
while(!q.empty())循环:循环依次取出同一步数能走到的点,再往前走一步。
-
int dx[4] = {0, 1, 0, -1}, dy[4] = {-1, 0, 1, 0};:一个点往下一步走得时候,可以往上下左右四方向走。
代码
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int g[N][N];//存储地图
int f[N][N];//存储距离
int n, m;
void bfs(int a, int b)//广度优先遍历
{
queue<PII> q;
q.push({a, b});
//初始点的距离为 0.
//可以不要这一句,因为f初始化的时候,各个点为0
f[0][0] = 0;
while(!q.empty())
{
PII start = q.front();
q.pop();
//这一句可以不要,因为入队的时候就置为了1
g[start.first][start.second] = 1;
int dx[4] = {0, 1, 0, -1}, dy[4] = {-1, 0, 1, 0};
for(int i = 0; i < 4; i++)//往四个方向走
{
//当前点能走到的点
int x = start.first + dx[i], y = start.second + dy[i];
//如果还没有走过
if(g[x][y] == 0)
{
//走到这个点,并计算距离
g[x][y] = 1;
f[x][y] = f[start.first][start.second] + 1;//从当前点走过去,则距离等于当前点的距离+1.
//这个点放入队列,用来走到和它相邻的点。
q.push({x, y});
}
}
}
cout << f[n][m];
}
int main()
{
memset(g, 1, sizeof(g));
cin >> n >>m;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
cin >> g[i][j];
}
}
bfs(1,1);
}
Java代码
/***
* 做这种题目的步骤(最短路问题)
*1.创建两个存储,一个存储值,一个存储距离
*2.然后首先将第一个点的位置存储的距离提前标注出来
*3.然后弄两个方向变量用于上下左右前进int[] dx = {-1,0,1,0}, dy = {0,1,0,-1};
*4.然后如果四个方向上的点没有超过边界,在结合实际情况有没有用过的点,
* 判断能不能够进行前进,如果可以就进行前进存储其内容g跟距离d+1
* 5.最后返回想要的最短值d;
* **/
import java.io.*;
public class Main{
static int N = 110,hh,tt,n,m;
static int[][] g = new int[N][N];//用来存储迷宫地图
static int[][] d = new int[N][N];//用来存储走的距离
static PII[] q = new PII[N*N];//用来放每个点的下标
public static int bfs(){
hh = 0 ; tt = -1; //队列的头节点=0,尾节点 = 0;
d[0][0] = 0; // 我们首先站在的是第一个点,所以值距离设置为0
q[++tt] = new PII(0,0); //然后将第一个点下标存入q队列中
//利用向量的方法进行让他上下左右判断是否能够前进
int[] dx = {-1,0,1,0};//上(-1,0) 下(1,0)
int[] dy = {0,1,0,-1};//左(0,-1) 右(0,1)
while(hh <= tt){
PII t = q[hh++]; //每一次将头结点拿出来
for(int i = 0 ; i < 4 ; i ++ ){//然后进行下一步要往哪里走,这里可能有多重选择可走
int x = t.first + dx[i]; //这里进行x轴向量判断
int y = t.second + dy[i];//这里进行y轴向量的判断
//如果x,y满足在地图中不会越界,然后地图上的点g是0(表示可以走),
//然后这里是没走过的距离d是-1;
if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1){
//将现在可以走的点(x,y)加上上一个点计数距离的点加上一,就是现在走到的点的距离
d[x][y] = d[t.first][t.second] + 1;
q[++tt] = new PII(x,y);//然后将这一个可以走的点存入队列尾
}
}
}
return d[n-1][m-1]; //最后返回的是地图走到尽头最后一个位置的位置统计的距离
}
public static void main(String[] args)throws IOException{
BufferedReader re = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter wt = new BufferedWriter(new OutputStreamWriter(System.out));
String[] s = re.readLine().split(" ");
n = Integer.parseInt(s[0]);
m = Integer.parseInt(s[1]);
for(int i = 0 ; i < n ; i ++ ){
String[] st = re.readLine().split(" ");
for(int j = 0 ; j < m ;j ++ ){
g[i][j] = Integer.parseInt(st[j]);
d[i][j] = -1;
}
}
System.out.println(bfs());
wt.close();
}
}
//这是一个用来存储两个坐标的类Pair
class PII{
int first,second;
public PII(int first,int second){
this.first = first;
this.second = second;
}
}
打印路径
#include<bits/stdc++.h>
using namespace std;
const int N = 200;
int n,m;
int d[N][N];//存储从起点到各点的最短距离,初始化为-1,表示未访问过。
int g[N][N];//存储地图信息,0表示可以通过的点,非0表示有障碍物的点。
queue<pair<int,int>> q; //用于BFS搜索的队列,存储点的坐标。
pair<int, int> prevNode[N][N]; //存储每个点的前一个点的坐标,用于追踪路径
int bfs(){
memset(d,-1,sizeof d);// 初始化所有点的最短距离为-1
d[1][1] = 0; //首先将起点(1, 1)的最短距离设置为0,表示从起点到起点的距离为0,
q.push({1,1}); //把起点放入队列中。
int dx[4] ={0,0,-1,1},dy[4] = {1,-1,0,0};//上下左右
while(q.size()){//当队列中还有坐标
auto t = q.front(); // 获取队列前端元素,即当前处理的点
q.pop(); // 弹出当前处理的点
for(int i = 0;i < 4;i++){
int x = t.first + dx[i],y = t.second + dy[i];//遍历四个方向
//如果这个相邻点有效(在网格范围内)、未被访问过(d[x][y] == -1)、且没有障碍物(g[x][y] == 0),
if(x >= 1 && y >= 1 && x <= n && y <= m && d[x][y] == - 1 && g[x][y] == 0){//记住是y <= m不是y <= n
d[x][y] = d[t.first][t.second] + 1; //更新这个点的最短距离为d[t.first][t.second] + 1
prevNode[x][y] = t; // 记录前驱点,是由t来到(x,y)的。
q.push({x,y}); //将其坐标加入队列中。
}
}
}
//循环结束后,d[n][m]中存储的就是从起点(1, 1)到终点(n, m)的最短距离。
//如果终点不可达,结果将保持为初始化时的-1。
return d[n][m];
}
void print_path() {
if (d[n][m] == -1) {
cout << "终点不可达。" << endl;
return;
}
vector<pair<int, int>> path;
// 从终点开始逆向追踪到起点
//这里为什么逆向追踪呢?因为我们储存的是前驱节点,我们只知道到达了终点(n,m),所以要先找(n,m)的前驱节点a,
//再找a的前驱节点b,直到到达(1,1)
//这个过程就像是沿着一条线索,从故事的结局逐步回溯到开头一样。
//make_pair(1, 1) 创建了一个包含两个整数的 pair
for (pair<int, int> at = {n, m}; at != make_pair(1, 1); at = prevNode[at.first][at.second]) {
path.push_back(at);
}
path.push_back({1, 1}); // 加入起点
reverse(path.begin(), path.end()); // 将路径逆序,因为我们是逆向追踪的
for (auto p : path) {
cout << "(" << p.first << ", " << p.second << ")" << " -> ";
}
cout << "End" << endl;
}
int main() {
cin >> n >> m;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
cin >> g[i][j];
}
}
cout << bfs() << endl; // 执行BFS搜索并输出从起点到终点的最短距离
print_path(); // 打印找到的路径
return 0;
}

![[VulnHub靶机渗透] Hackademic: RTB1](https://img-blog.csdnimg.cn/direct/85926679e44140de8d1d2fc264b1736c.png)