🔥 引言

在现代计算机科学与软件工程的实践中，高效数据检索是众多应用程序的核心需求之一。二分查找算法，作为解决有序序列查询问题的高效策略，凭借其对数时间复杂度的优越性能，占据着算法领域里举足轻重的地位。本篇内容旨在全面剖析二分查找算法的内在机制、实施步骤、性能特点及其在实际应用中的考量，为深入理解和有效应用此算法提供坚实的基础。📚

---

🌐 基础概念入门

什么是二分查找❓

想象一下，你站在一列整齐排列的书架前，想要找到某本书。

传统的做法是从头开始一本本地找，但如果你知道书架上的书是按字母顺序排列的，聪明的做法是直接走到中间，如果目标书在中间就找到了，不在的话根据书名比较判断是在左边还是右边的书架继续寻找。这就是二分查找的基本思想。🔍

如何工作❓

• 有序数组：二分查找的前提是数组必须是有序的，无论是升序还是降序。
• 分而治之：算法每次都将搜索区间缩小一半，通过比较中间元素来决定是在左半部分还是右半部分继续查找。
• 递归或迭代：二分查找可以递归或迭代实现，选择哪种方式取决于个人偏好和具体应用场景。

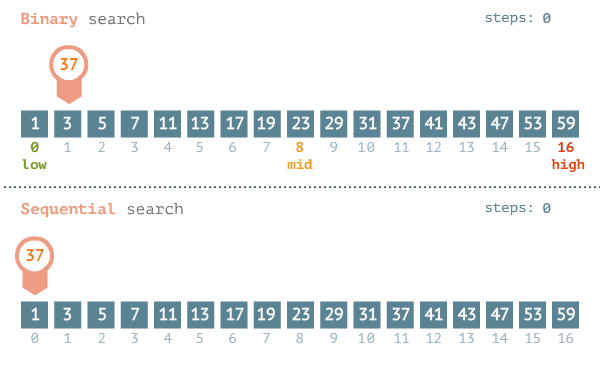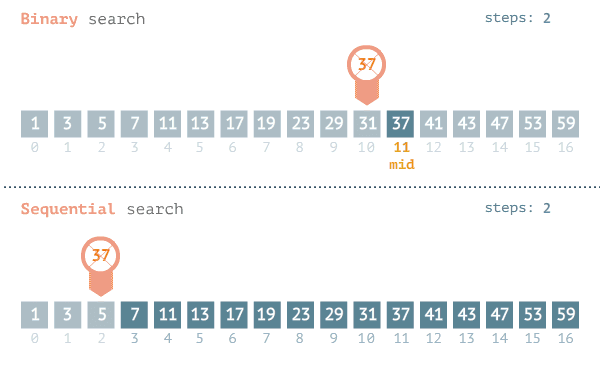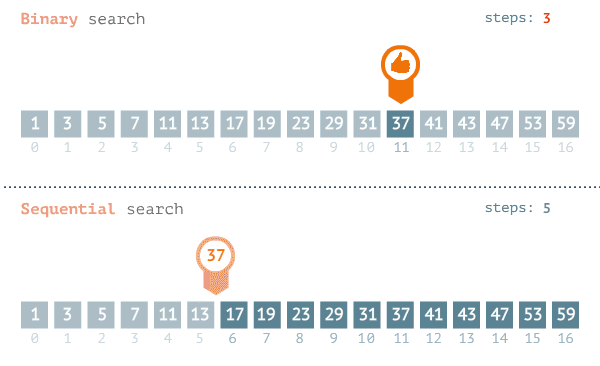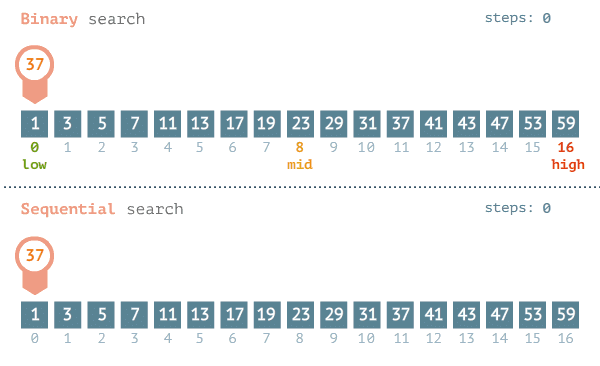
工作示例：

下面的示例说明了二分查找的工作原理。我随便想一个 1～100 的数字。你的目标是以最少的次数猜到这个数字。你每次猜测后，我会说小了、大了或对了。假设你从 1 开始依次往上猜，猜测过程会是这样。

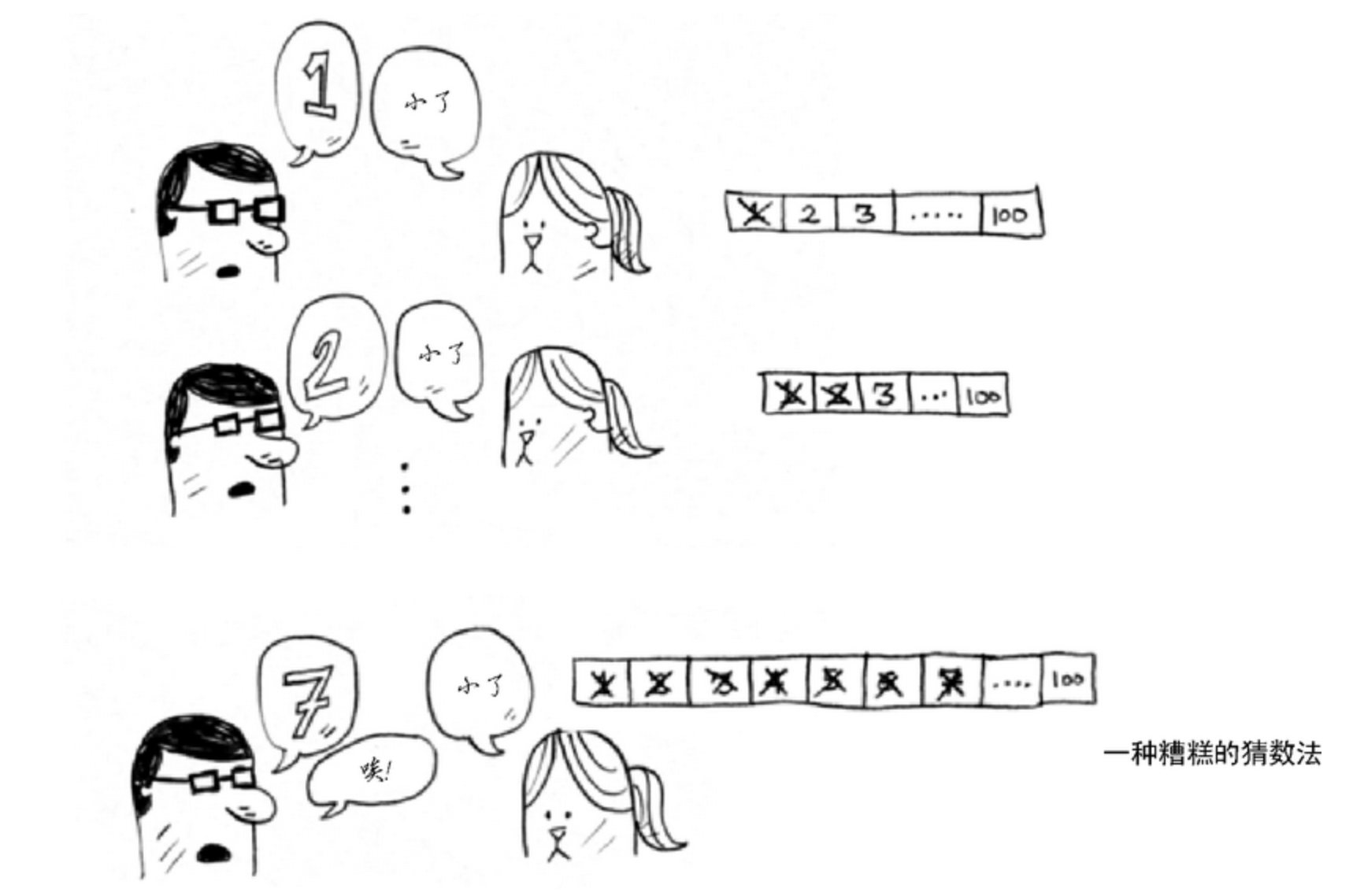
这是 简单查找，更准确的说法是傻找。每次猜测都只能排除一个数字，在最糟糕的情况下需要100次才能够找到这个数字。

而二分查找直接从有序列表的中间开始，一次就将排除一半的数字：

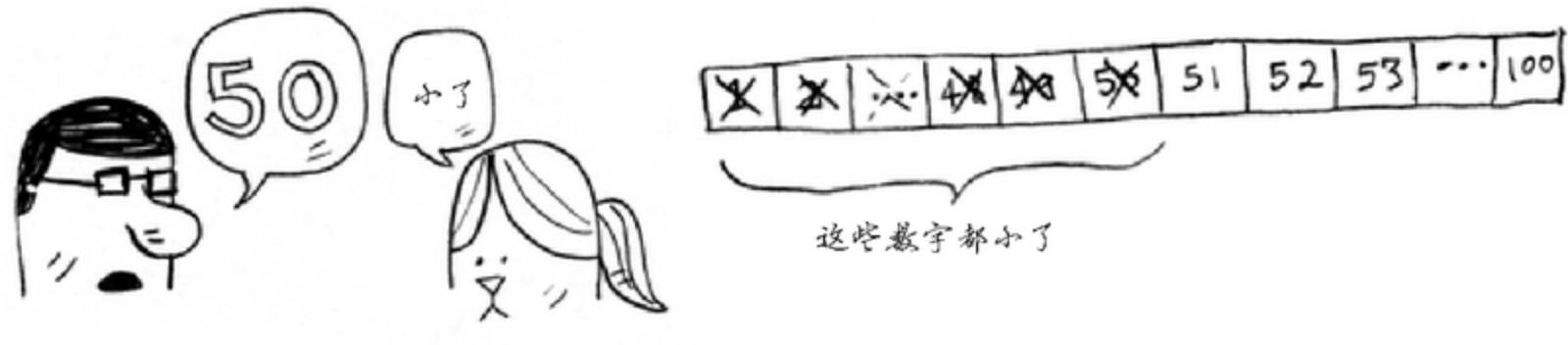
随后再从剩下的数字(50-100)的中间数(75)进行判断，又将排除掉一半的数字：

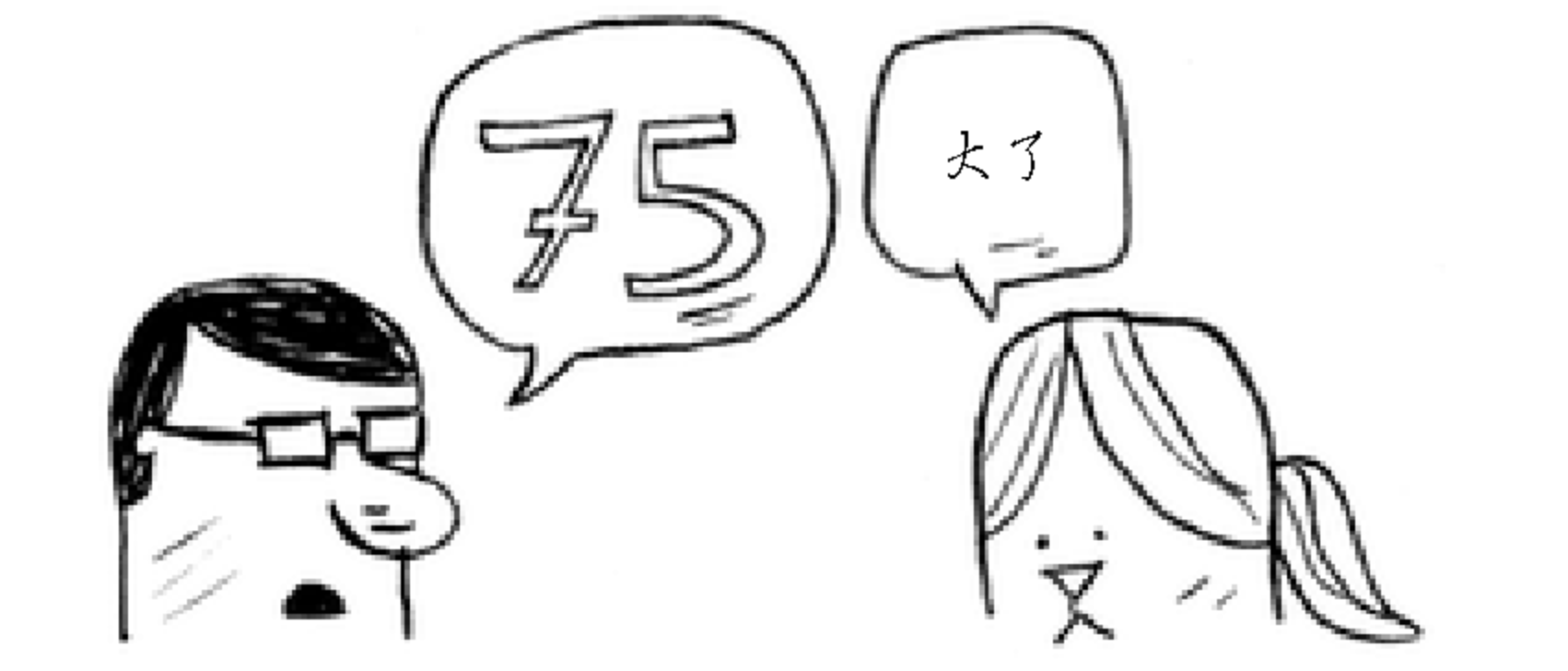
随后再从数字(50-75)的中间数进行判断，以此类推：找到最后的数：

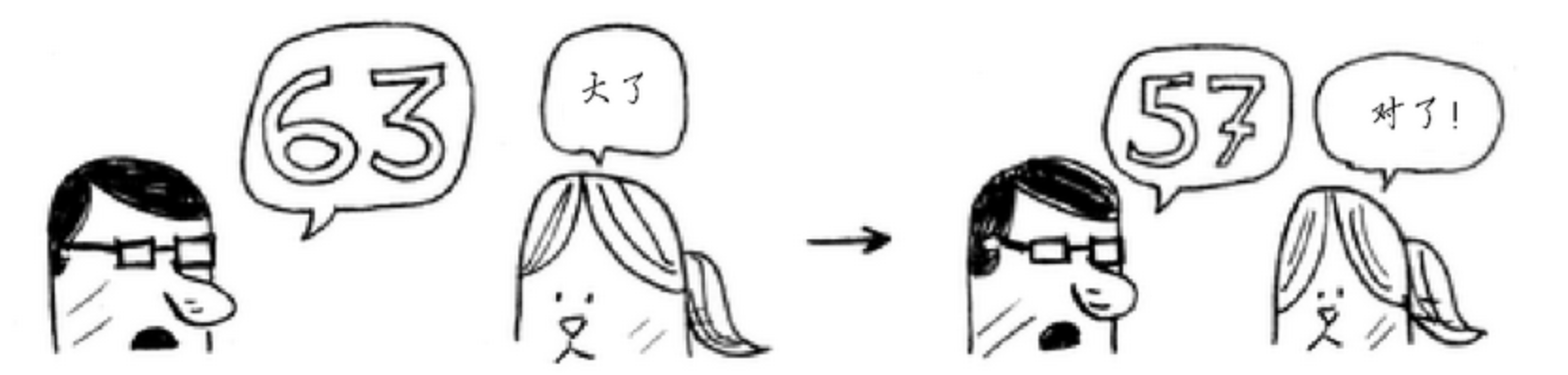
也就是说，100个元素的情况，使用二分查找最糟糕的情况也只需要7步就可以查找到相应的数字，比简单查找要少多了！

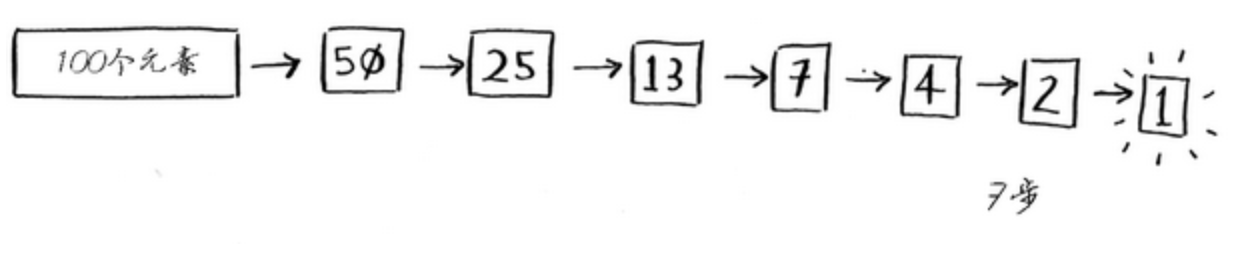
上述示例来自 力扣——算法图解

🔍 算法步骤详述

1. 初始化指针：设置两个指针，left初始为0，表示数组起始位置；right初始为数组最后一个元素的索引。

2. 计算中间索引：为了避免整数溢出，通常采用mid = left + (right - left) / 2。

3. 比较并调整区间：

   • 若array[mid] == target，直接返回mid。
   • 若array[mid] < target，说明目标在右半部分，更新left = mid + 1。
   • 若array[mid] > target，则目标在左半部分，更新right = mid - 1。

4. 重复步骤2和3，直到left > right，此时说明数组中不存在目标值，返回-1或其他表示未找到的值。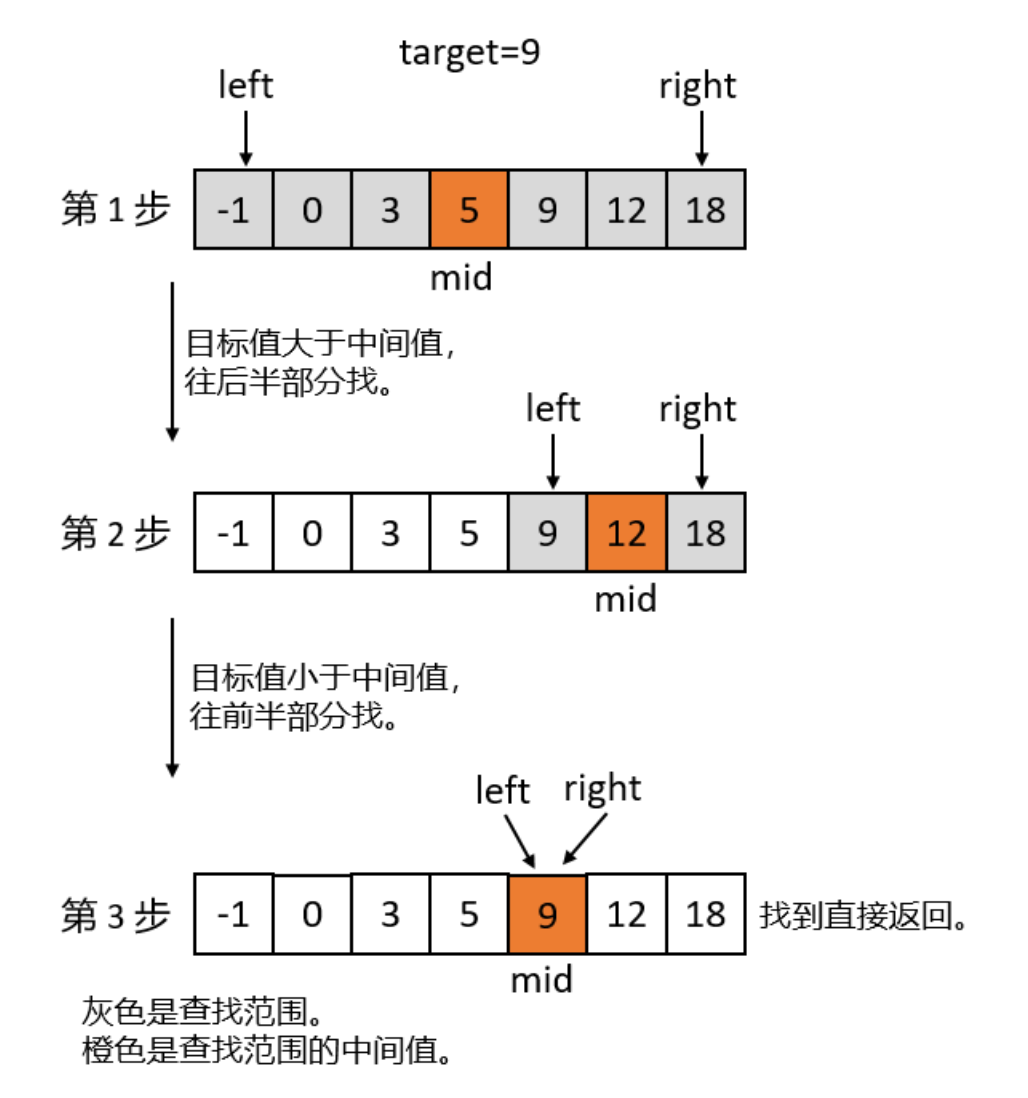

   

🧩 进阶理解

📌 大O表示法与时间复杂度分析

在深入探讨二分查找之前，了解大O表示法这一衡量算法效率的重要工具是不可或缺的。大O表示法用于描述算法在最坏情况下的时间复杂度，即随着输入数据量增长，算法执行时间增长的速度。它关注的是上界分析，帮助我们理解算法在大规模数据处理时的性能表现。

🍭 大O表示法简介

• 符号意义：“O”表示“Order of”，用来描述算法运行时间的增长率。
• 重点在于增速：它并不精确测量算法执行的确切时间，而是关注于当输入大小（通常用n表示）增加时，算法执行时间增长的速率。
• 简化原则：忽略常数因子和低阶项，专注于最高阶项，因为当n足够大时，这些因素对整体趋势影响不大。

大 O 表示法指出了算法有多快。例如，假设列表包含n个元素。简单查找需要检查每个元素，因此需要执行n次操作。使用大 O 表示法，这个运行时间为 𝑂(𝑛)。单位秒呢？没有——大 O 表示法指的并非以秒为单位的速度。大 O 表示法让你能够比较操作数，它指出了算法运行时间的增速。

🍭 二分查找的时间复杂度

对于二分查找算法，每次迭代都将搜索区间减半，这意味着查找次数与输入数据的对数成正比。因此，二分查找的时间复杂度为O(log n)。

🍭 与简单查找对比

为了更好地理解二分查找的效率，我们可以将其与简单（顺序/线性）查找进行对比：

• 简单查找（也称顺序/线性查找）：在无序或有序列表中从头到尾遍历，直到找到目标值或遍历完整个列表。其时间复杂度为𝑂(𝑛)，意味着随着数据量的增加，查找时间线性增长。

• 二分查找：在有序列表中通过不断缩小搜索范围来查找目标值。时间复杂度为𝑂(log 𝑛)，表明当数据量翻倍时，所需查找步骤仅增加log(𝑛)次，这是一种远低于线性增长的速度。

🍭 时间增速对比

• 简单查找的时间增速与数据量成正比，直观理解就是数据每增加一倍，查找时间大致也增加一倍。在大数据集上，这种增长速度很快变得不可承受。

• 二分查找的时间增速则要慢得多，因为它基于对数函数。例如，即使数据量从1000增加到100万，二分查找所需的步骤只增加大约从10增加到20（基于2为底的对数），这种增长速率在处理大量数据时显得极为高效。

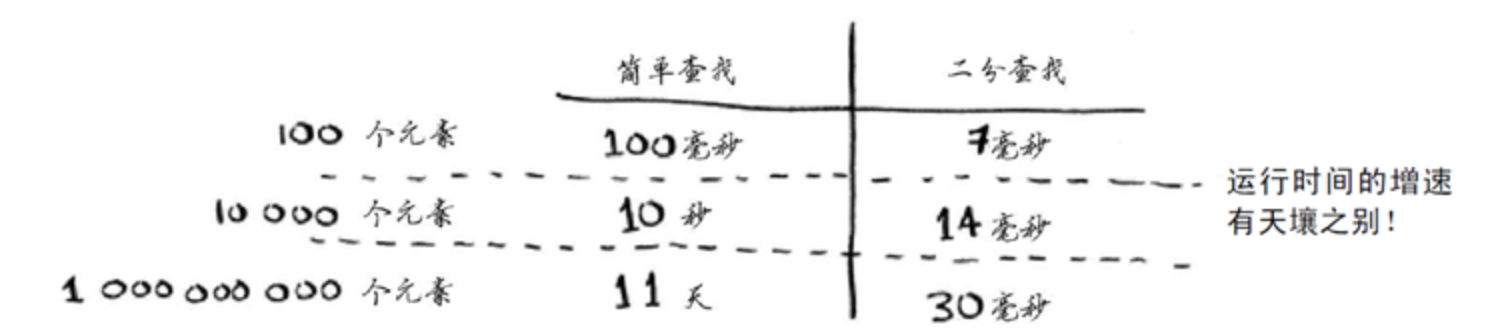
如图所示：假如查找100个元素使用简单查找需要100毫秒，使用二分查找需要7毫秒，可能这个差距可以让人接受。当数据增多时，查找1000000000个元素需要11天才可以查找完毕，而使用二分查找仅仅只需要30毫秒，比使用简单查找查询100个元素还要快的多！

简单查找（也称为顺序查找）的时间复杂度为𝑂(𝑛)，这意味着如果数据量增加，查找所需的时间也会直接线性地增加:

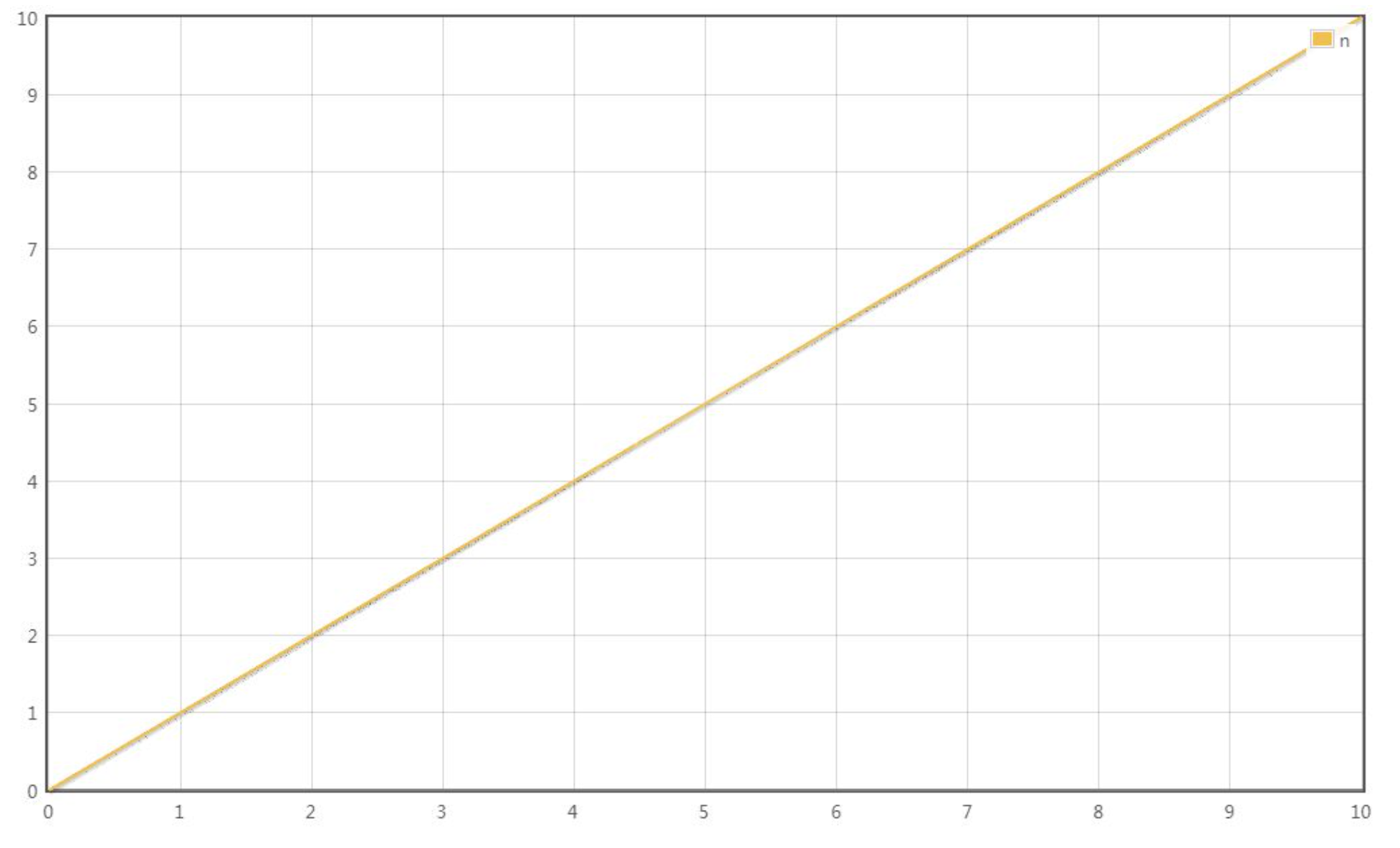
二分查找的时间复杂度为𝑂(log 𝑛)，这意味着随着数据量n的增大，二分查找所需时间的增速远低于线性查找,它与数据量的对数成正比，而非与数据量本身成正比:

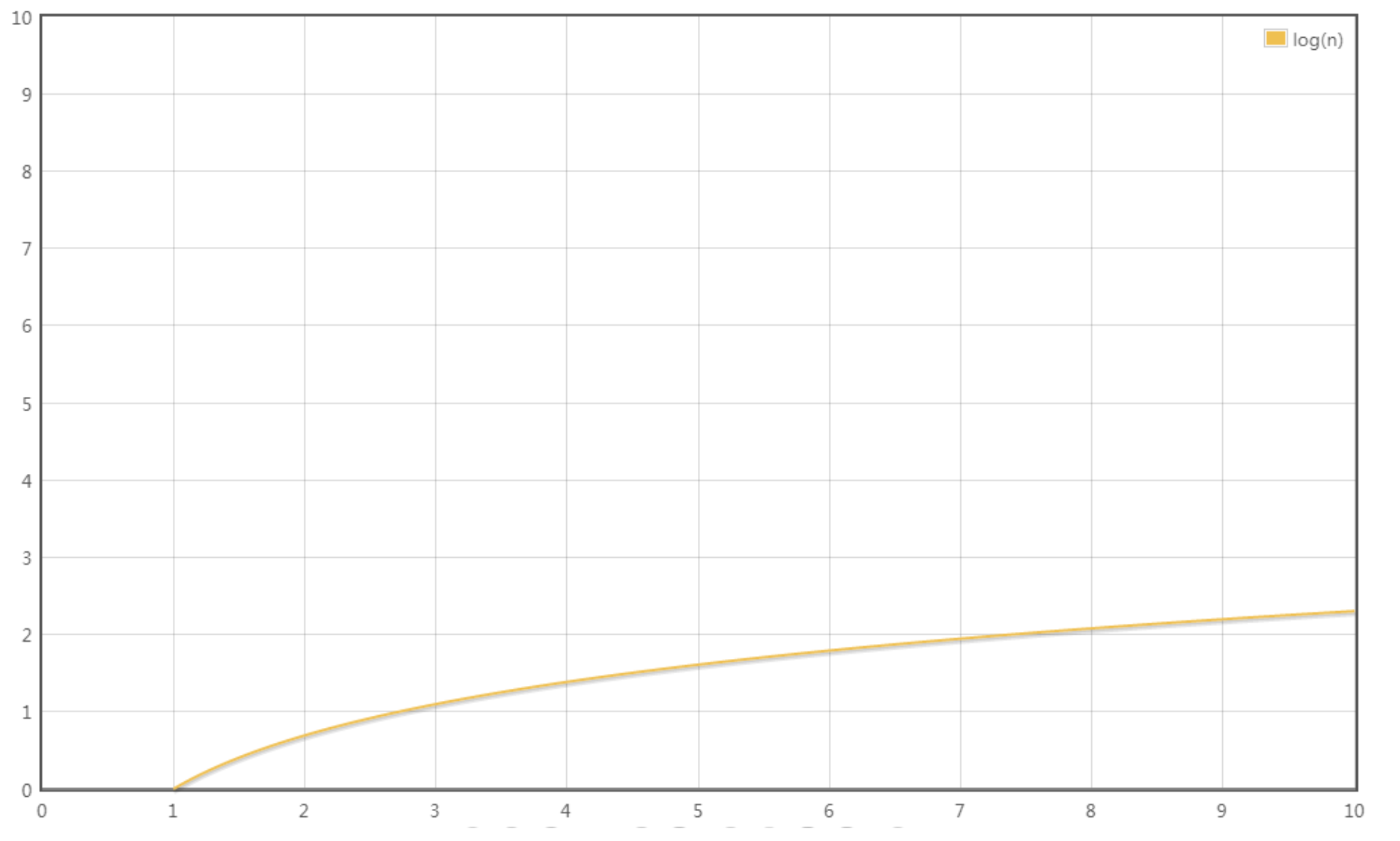
综上所述，二分查找由于其对数级的时间复杂度，在处理大规模有序数据集时，相比线性查找有着显著的性能优势，特别是在数据规模庞大的情况下，这种优势体现得更为明显。

---

📈 实践案例：JavaScript代码示例

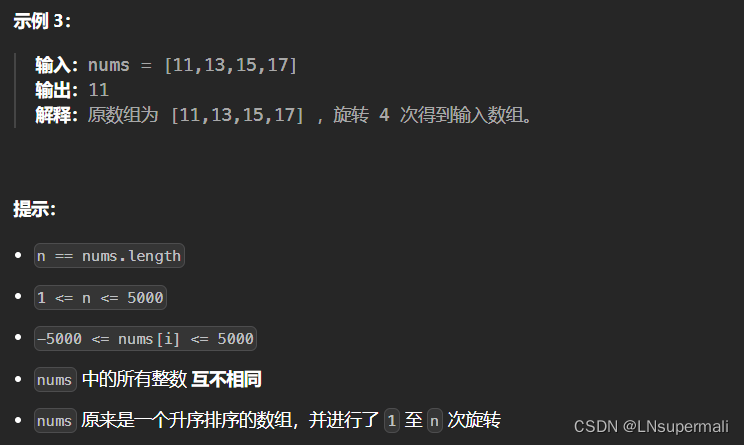
给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

/**
 * @param {number[]} nums  // 传入一个有序的整型数组nums
 * @param {number} target  // 需要查找的目标值target
 * @return {number}         // 返回目标值在数组中的索引，如果未找到则返回-1
 */
const search = function (nums, target) {
	let left = 0, right = nums.length - 1;  // 初始化左右边界，left为数组起始索引，right为数组结束索引
	let result = -1;  // 初始化结果变量result为-1，表示目标值未找到

	// 当左边界小于等于右边界时，继续循环
	while (left <= right) {
		let mid = left + Math.floor((right - left) / 2);  // 计算中间索引mid，使用Math.floor向下取整保证mid为整数

		// 如果中间元素等于目标值
		if (nums[mid] === target) {
			result = mid;  // 更新result为找到的目标值索引
			right = mid - 1;  // 调整右边界继续在左半部分查找（若需查找重复值应调整此处逻辑）
		}
		// 如果中间元素小于目标值
		else if (nums[mid] < target) {
			left = mid + 1;  // 缩小查找范围至右半部分，更新左边界
		}
		// 如果中间元素大于目标值
		else {
			right = mid - 1;  // 缩小查找范围至左半部分，更新右边界
		}
	}

	return result;  // 循环结束，返回最终查找结果
};

// 示例使用
const sortedArray = [-1,0,3,5,9,12];  // 定义一个已排序的数组
console.log(search(sortedArray, 9));  // 在数组中查找数字9，并打印查找结果为 4

---

📌 总结

二分查找算法是针对有序数组高效查找特定元素的方法。其核心机制在于每次比较数组中间元素，根据比较结果将查找范围减半，直至找到目标或确定目标不存在。这一过程展现了𝑂(log 𝑛)的时间复杂度，意味着数据量每翻一倍，查找操作的次数只需增加一个固定比例（基于对数增长），而非线性增长。相比之下，线性查找的时间复杂度为𝑂(𝑛)，数据量增长时效率下降明显。

大O表示法作为衡量算法效率的标准，帮助我们抽象理解算法随输入规模变化的性能表现，关注上界分析，忽略了常数项和低阶项，专注于影响最大的部分。在算法设计与分析中，它是评估和比较不同方案效率的有力工具。

总之，二分查找凭借其对数时间复杂度，在处理大规模有序数据时表现出色，是算法工具箱中不可或缺的高效利器。而对于任何算法的学习，理解大O表示法都是基础且关键的一步，它让我们能够科学地预测和优化程序的执行效率。