推文作者信息:杨春苇,香港城市大学系统工程系在读博士生,研究方向: 专注于线上平台的服务运营管理,涵盖匹配、定价、调度和路径规划等问题。通过将数据科学与运筹优化相结合,提供高效实用的决策支持系统。
编者按:
电子商务和现代零售近些年迅速发展,送货上门成为一种重要的服务模式。消费者需求的多样化和即时满足期望的上升对送货上门服务的质和量都有新的要求。因此,送货上门服务中优化问题的研究也日益增多,这些研究试图分析和改进配送过程中的各个环节,从而提高效率、降低成本,并提升客户满意度。虽然不同研究的具体焦点可能有所不同,但它们共同关注的是如何在保证服务质量的前提下,优化物流配送的效率和提高企业的收益。
本期我们重点推荐三篇相关文章,内容涵盖从宏观的消费者偏好分析到运营层面的不确定性处理,以及更具体的车辆调度和配送路线优化等多个方面。
1.我们分享的第一篇论文来自Management Science,该文探讨了如何更好地设计送货时间以提高顾客满意度并增加收入。作者构建了离散选择模型,通过分析在线数据研究顾客对于不同送货时间属性的偏好,从而为零售商提供针对性的配送策略,以此提升服务质量和经济效益。
2.我们分享的第二篇论文来自Transportation Science,针对外卖配送问题中顾客下单时间和餐厅备餐时间的不确定性,该文构建了基于路径的马尔可夫决策模型,据此优化送餐时间和路线以减少配送延误,提高服务效率和顾客满意度。
3.我们分享的第三篇论文同样来自Transportation Science,该文研究了在线购物的同日达配送问题,作者建立了马尔可夫决策模型,通过对车辆调度和路线的优化,帮助物流公司更有效地处理配送服务中遇到的动态和不确定性问题。
Customer Preferences for Delivery Service Attributes in Attended Home Delivery
Reference: Amorim, Pedro, et al. “Customer preferences for delivery service attributes in attended home delivery.” Management science (2024).
原文链接: https://pubsonline.informs.org/doi/full/10.1287/mnsc.2020.01274
Problem:
零售商需要研究如何更好地将线上购买的商品交付给顾客,从而提高顾客满意度。作者通过实证研究方法,利用欧洲一家大型杂货零售商的在线顾客订单数据,探究顾客对于送货上门时间属性的偏好(包括配送速度speed、送货时间精确度precision和可选时间timing)。
Method:
基础模型
作者采用了条件逻辑回归模型 (conditional logit model)来分析消费者在多个送货上门选项中的你不同选择,这实际上与选品问题类似。在选品问题中,消费者需要在多个产品或服务中选择一个,而在这里,消费者的选择对象是不同的送货时间段。这一模型基于效用最大化原理(utility maximizing),假设顾客会从各个可用的时间段中选择一个时段最大化其效用。
模型的形式通常为:
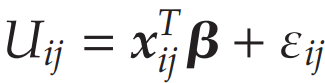
其中, U是消费者对于选择项效用,𝑥 是与选择项相关的属性向量,β 是属性参数的向量,而 ϵ 是误差项
在作者的模型设置中,每个送货上门选择项都有特定的属性,例如送货速度(LEADTIME)、时间窗大小(SLOTSIZE)、时间段(TIME-OF-DAY)和星期几(DAY-OF-WEEK),这些属性被包括在 𝑥 向量中。
本文的基础模型如下:
U
i
j
=
β
1
PRICE
i
j
+
β
2
LEADTIME
i
j
+
β
3
SLOTSIZE
j
+
∑
h
β
h
TIME-OF-DAY
i
j
h
+
∑
d
β
d
D
A
Y
−
O
F
−
W
E
E
K
i
j
d
+
λ
μ
i
j
+
η
i
j
+
ε
~
i
j
\begin{aligned} U_{i j}= & \beta_1 \text { PRICE }_{i j}+\beta_2 \text { LEADTIME }_{i j}+\beta_3 \text { SLOTSIZE }_j \\ & +\sum_h \beta_h \text { TIME-OF-DAY }{ }_{i j}^h+\sum_d \beta_d D A Y-O F-W E E K_{i j}^d \\ & +\lambda \mu_{i j}+\eta_{i j}+\tilde{\varepsilon}_{i j} \end{aligned}
Uij=β1 PRICE ij+β2 LEADTIME ij+β3 SLOTSIZE j+h∑βh TIME-OF-DAY ijh+d∑βdDAY−OF−WEEKijd+λμij+ηij+ε~ij
其中,U代表顾客 i 从选择时间段 j 中获得的效用;PRICE代表时段的价格。
模型的调整
基础模型面临价格内生性的问题,这通常是由于价格变量受到未观察因素的影响。若未进行适当处理,这可能导致模型参数估计出现偏差。为了解决价格内生性问题,文章选择了由 Petrin 和 Train (2010) 提出的控制函数方法(control function approach)。这种方法在处理价格内生性时提供了很大的灵活性,对于大型数据集,其计算也需求相对较低。具体来讲,该方法首先通过回归分析计算价格与潜在影响因素之间的关系,从而得到价格的残差。随后,将这些残差作为控制变量引入到主效用模型中,以校正潜在的内生性偏差。调整后的模型更为精确,能够有效地反映价格对消费者选择行为的真实影响。
本文的最终模型如下:
U
i
j
=
β
1
PRICE
i
j
+
β
2
LEADTIME
i
j
+
β
3
SLOTSIZE
j
+
∑
h
β
h
TIME-OF-DAY
i
j
h
+
∑
d
β
d
D
A
Y
−
O
F
−
W
E
E
K
i
j
d
+
λ
μ
i
j
+
η
i
j
+
ε
~
i
j
\begin{aligned} U_{i j}= & \beta_1 \text { PRICE }_{i j}+\beta_2 \text { LEADTIME }_{i j}+\beta_3 \text { SLOTSIZE }_j \\ & +\sum_h \beta_h \text { TIME-OF-DAY }{ }_{i j}^h+\sum_d \beta_d D A Y-O F-W E E K_{i j}^d \\ & +\lambda \mu_{i j}+\eta_{i j}+\tilde{\varepsilon}_{i j} \end{aligned}
Uij=β1 PRICE ij+β2 LEADTIME ij+β3 SLOTSIZE j+h∑βh TIME-OF-DAY ijh+d∑βdDAY−OF−WEEKijd+λμij+ηij+ε~ij
其中,λμ是用来调整价格内生性的控制函数,η是指标准的独立同分布正态分布误差项,其期望值为零。
Main results:
- 首先,顾客平均愿意为减少一小时的配送时间支付€0.04;其次,顾客对送货时间精确度(即更窄的配送时间窗)的偏好更为强烈,愿意为缩窄一小时的配送时间窗支付€0.45。此外,顾客对于配送的时间段也有显著的偏好,一般更倾向于在早晨或晚间接收配送,并且尤其偏好周五,而对周日的配送偏好最低。
- 结果还表明,高价值订单的顾客对送货上门时间属性的支付意愿明显高于平均水平,例如,对于价值超过€200的订单,顾客愿意为减少一小时配送时间支付近€1;订单中含有新鲜商品的顾客对配送速度和送货时间精确度的支付意愿更高;顾客忠诚度(如购买频率和总购买金额)也是影响支付意愿的重要因素。
Why recommends?
该研究通过采用条件逻辑回归模型和控制函数等计量经济学方法,有效处理了价格内生性问题,并深入探讨了顾客偏好的异质性。利用大规模实证数据分析,揭示了顾客对配送时间属性的具体偏好和支付意愿。通过分析顾客的订单特征和偏好异质性,丰富了对顾客行为理解的深度,还为零售商提出了如何根据顾客需求优化配送时间的管理建议,指导零售商实施个性化服务和细分市场策略。研究紧贴当前电商快速发展和消费者购物习惯变化的背景,具有理论创新和实际应用价值。
The Restaurant Meal Delivery Problem: Dynamic Pickup and Delivery with Deadlines and Random Ready Times
Reference: Ulmer, Marlin W., et al. “The restaurant meal delivery problem: Dynamic pickup and delivery with deadlines and random ready times.” Transportation Science 55.1 (2021): 75-100.
原文链接: https://pubsonline.informs.org/doi/10.1287/trsc.2020.1000
Problem:
文章讨论了餐厅送餐问题(restaurant meal delivery problem,RMDP),该问题中一组司机需要从多个餐馆取餐并送至顾客处,每个订单有截止时间,并且餐厅的出餐时间是随机的。文章在考虑随机准备时间和截止时间的情况下,决策是否接受新订单以及如何调整送餐路线以最小化配送延误。
Method:
文章将RMDP建模为基于路线的马尔可夫决策过程(Route-Based Markov Decision Process),并通过预期客户分配策略(Anticipatory Customer Assignment,ACA) 进行求解。ACA策略主要通过推迟分配(Postponement)、时间缓冲(Time Buffer)和启发式分配方法(Assignment Heuristic)三个部分来RMDP问题中的不确定性和动态性。
- 决策时刻(Decision Points):新顾客订单到达或特定的推迟时间结束时。
- 状态空间(State Space):由当前时间、已接订单的集合、每辆车的位置和每辆车的路线计划组成。每个订单包括订单时间、餐馆位置、指派的司机和装载状态。
- 决策空间(Action Space):在每个决策点,决策包括是否将新订单分配给某个司机或推迟分配,以及如何更新司机的路线计划。
- 目标函数(Objective Function): 找到一个最优策略,该策略能最小化期望延迟,即所有订单的交付时间和截止时间之间差值绝对值的总和。
文章中的预期客户分配策略包含以下几个方面:
- 推迟分配(Postponement):
允许某些订单的分配决策被推迟,以待更多信息变得可用,从而提高分配的灵活性和效率。 - 时间缓冲(Time Buffer):
通过在计划到达时间上增加一个缓冲时间,来减少因准备时间不确定性或新订单插入导致的延误风险,提高对未来不确定性的抵抗力。 - 分配启发式(Assignment Heuristic):
该方法通过评估所有未分配订单可能的序列和每个序列下的车辆分配,寻找导致最小预期延迟增加的订单分配方案。这一过程中,考虑了各种分配方案对整体延迟的影响,以选择最优的订单分配序列。
Main results:
作者将ACA策略与立即配送策略(每当有订单产生时,系统立即将订单分配司机)对比,结果表明,ACA策略能够显著提高各方利益相关者的满意度,具体包括:
- 对顾客而言,ACA策略在所有实验设置中,与立即策略相比,都能显著降低客户的平均最大延迟。例如,在订单量为300的实验设置中,客户每天经历的平均最大延迟不超过15分钟,而最快策略下超过24分钟 。
- 对餐馆而言,ACA策略避免了食物送达时间过长导致的品质下降问题,有助于提升顾客满意度和未来订单量。
- 对司机而言,ACA策略通过优化订单分配和路线规划,有助于减少司机的空驶时间和等待时间,从而提升司机的工作效率。
Why recommends?
文章的一个亮点在于同时考虑了客户请求的随机性和订单准备时间的不确定性。这两个因素增加了调度的复杂度,对餐饮送餐服务的运营管理构成了挑战。
- 对于随机客户请求:文章建模并分析了客户订单的动态请求,这些请求随时间变化且位置分布不定,使得送餐服务需要动态调整以应对这种变化。这种动态性要求送餐服务在不完全信息下做出快速有效的决策。
- 对于随机准备时间:除了处理客户订单的不确定性外,文章还考虑了订单准备时间的随机性。即订单从餐馆准备到可以送餐的时间不是固定的。
文章另一个亮点在于引入了一种基于预期和策略性推迟的处理机制,即通过推迟分配策略和时间缓冲来应对订单的不确定性。这种处理机制允许在收集到更多信息后再做决策,从而提高送餐效率。
The Same-Day Delivery Problem for Online Purchases
Reference: Voccia, Stacy A., Ann Melissa Campbell, and Barrett W. Thomas. “The same-day delivery problem for online purchases.” Transportation Science 53.1 (2019): 167-184.
原文链接: https://pubsonline.informs.org/doi/epdf/10.1287/trsc.2016.0732
Problem:
文章解决的是在线购物同日送达问题(Same-Day Delivery Problem for Online Purchases, SDDP)。SDDP是指在线零售商承诺在顾客下单的同一天内完成订单的配送。具体来说,SDDP被定义为一个多车辆动态取送货问题(Multi-vehicle Dynamic Pickup and Delivery Problem, MDPDP),在该问题中,配送请求在服务当天动态出现,每个请求都有与之相关的送货截止时间或时间窗口。这些请求由一个或多个配送中心(仓库或实体店铺)中的车队来完成,车辆在完成配送后必须返回配送中心。决策包括每个配送请求分配的车辆、车辆的路线规划以及车辆出发的时刻,以确保每个请求都能在规定的时间窗内得到满足。决策目标是最大化给定时间内完成的请求数量,同时考虑到成本的最小化
Method:
作者通过马尔可夫决策过程对问题进行了建模:
- 决策时刻(Decision Points): 当新的请求到达或车辆完成任务返回仓库时。
- 状态空间(State Space):描述了决策时刻所有必要信息,包括当前时间、请求的位置与时间窗口、车辆的到达时间及其是否在仓库等待的指标。
- 决策空间(Action Space):每个决策时刻,对于集合中的每个请求,都需要决定将其分配给车队中的某辆车、等待分配或分配给第三方服务。
- 目标函数(Objective Function):找到一个最优策略,最大化在给定时间约束内能够通过现有车队完成服务的预期请求数量。
为了解决MDP模型中维度灾难问题,作者采取了前向动态规划和样本场景规划方法
5. 前向动态规划(Forward Dynamic Programming):由于MDP的状态空间和动作空间非常大,使得传统的后向动态规划方法不可行,因此作者采用了前向动态规划的方法。这种方法不直接求解Bellman方程,而是通过逐步前进的方式,在每个决策时刻选择动作,并利用样本场景来指导这些选择。
6. 样本场景规划方法(Sample-Scenario Planning Approach):在每个决策时刻,根据当前状态和随机样本构建不同的未来情景,对于每个情景,使用启发式方法(如变邻域搜索,VNS)来生成路线规划,通过对所有情景规划的分析,选择一个最佳方案作为指导当前决策的“杰出计划”(distinguished plan)。
Main results:
研究针对不同地理分布和时间约束下的当日送达问题(Same-Day Delivery Problem, SDDP)进行了一系列计算实验。实验基于修改的Solomon (1987)和Gehring与Homberger (1999)的VRPTW(Vehicle Routing Problem with Time Windows)数据集,主要关注客户位置信息。实验探讨了五种时间窗口类型:1小时和2小时的截止时间(TW.d1和TW.d2),以及基于请求到达时间的三种1小时时间窗口(TW.f、TW.h、TW.r)。通过对比带延迟和不带延迟,以及采用和不采用样本场景规划的方案,评估各种策略对服务效率的影响。参数设置选择了半小时的采样时间范围和10个场景样本。
- 采样的价值:在所有情况下,使用采样相比不使用采样,平均填充率更高。对于TW.h和TW.r类型,采样平均提供了9.86%的改进;对于TW.d1、TW.d2和TW.f类型,采样提供了平均1.99%的改进。
- 车辆数量的影响:为达到95%的服务水平,TW.d2和TW.f类型需要11辆车。而对于TW.h和TW.r类型,达到同等服务水平所需的车辆数显著更多,证明了时间窗口分布对服务效率的重要影响。
- 到达率的影响:当到达率提高时(例如,从0.001到0.004请求/分钟),可服务请求的比例随之下降。这说明,在有限的资源下优化路线的重要性。
- CPU时间:使用采样和延迟策略的平均CPU时间(across all time window types)为272.78秒,而仅使用采样的平均CPU时间为96.69秒。这表明虽然采样策略在提高服务水平方面有效,但也需要考虑其计算开销。
Why recommends?
SDDP问题的挑战在于,顾客请求是动态到达的,这要求配送决策必须即时做出,同时考虑到未来可能出现的新请求。在解决现实场景的大规模问题时,很容易遇到“维数灾难”的问题。文章提出了一个实际可行的解决方案,能够在考虑未来不确定性的情况下,为同日配送问题生成高效的路线规划。这种方法虽然不能保证找到绝对的最优解,但能够在实际应用中提供满意的解决方案。另外,文章所提出的策略和方法不仅适用于解决SDDP问题,也为其他需要动态决策和调度的问题提供了参考。



![[Unity常见小问题]打包ios后无法修改模型透明度](https://img-blog.csdnimg.cn/direct/99a63fd3c84040c5ba841a02c2714f30.png)