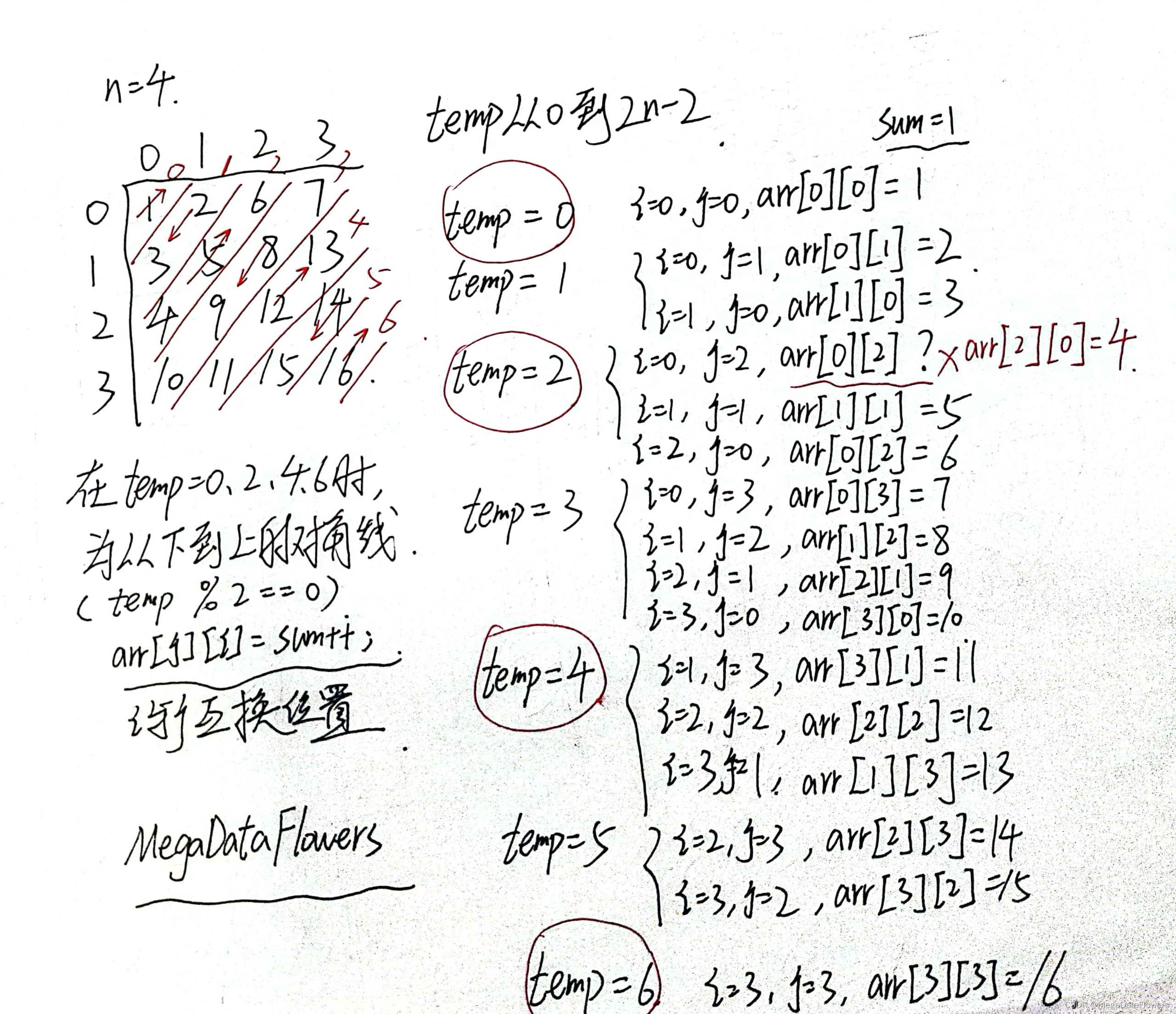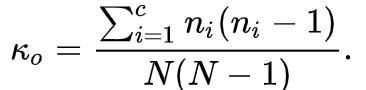T112524 【数组2】蛇形矩阵

题目来源

AC代码

#include<stdio.h>

int main()
{
    int arr[111][111];
    int n = 0;
    scanf("%d",&n);
    int temp = 0;
    int sum = 1;
    while(temp<=(2*n-2))
    {
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<n;j++)
            {
                if((i+j) == temp)
                {
                    if(temp%2 == 0){
                        arr[j][i] = sum++;       
                    }else{
                        arr[i][j] = sum++;
                    }
                }
            }
        }
        temp++;
    }
    
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            printf("%d ",arr[i][j]);
        }
        printf("\n");
    }
    return 0;
}

算法

**根据样例来分析**
输入：
4
输出：
1 2 6 7
3 5 8 13
4 9 12 14
10 11 15 16  

由7 8 9 10这条斜对角线可以得知：i+j=(n-1)
下面我就称这条对角线为中心对角线

---

在中心对角线前面的对角线分别为：
i+j=(n-2)、i+j=(n-3)…
在中心对角线后面的对角线分别为：
i+j=n、i+j=(n+1)…

---

设定一个temp变量，并且temp = i+j
让temp从0开始加到2*n-2

---

为什么是2*n-2呢？

因为数组的下标是从0开始的，所以说i+j最小为0，最大为2*n-2

---

因为最后要打印数字，所以说定义一个sum变量从1开始，不断累加，赋值给数组

---

因为以中心对角线为基准的左右两边的对角线：分为从上到下和从下到上两种，其中，从下到上的对应的(i+j)是偶数

---

过程推导：