本文为【intro】图卷积神经网络（GCN）-CSDN博客后续（因为经验告诉我超过2w字编辑器就会卡……）
第一部分还是进一步再看看GCN
图卷积神经网络GCN_哔哩哔哩_bilibili
回顾
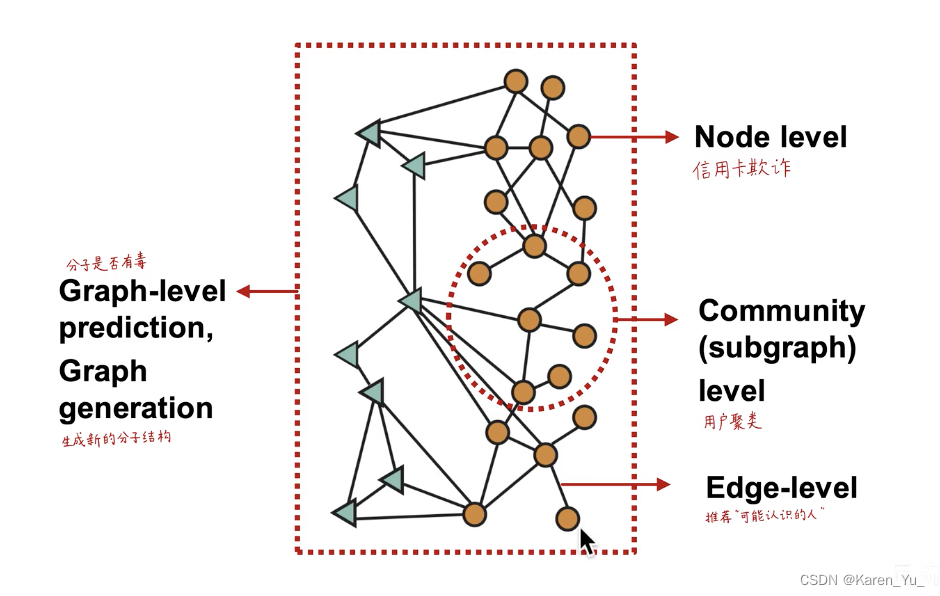
图神经网络的基本原理就是把图中的节点编码映射成一个低维、连续、稠密的d维向量。这里的d比如128、256。把图中的每一个节点编码成128（or256）维的向量，而这个向量是一维连续稠密的，能够反映这个节点在原图的连接和属性关系。两个节点对应的两个向量在d维空间的相似度，可以反映这两个向量（节点）在原图的相似度
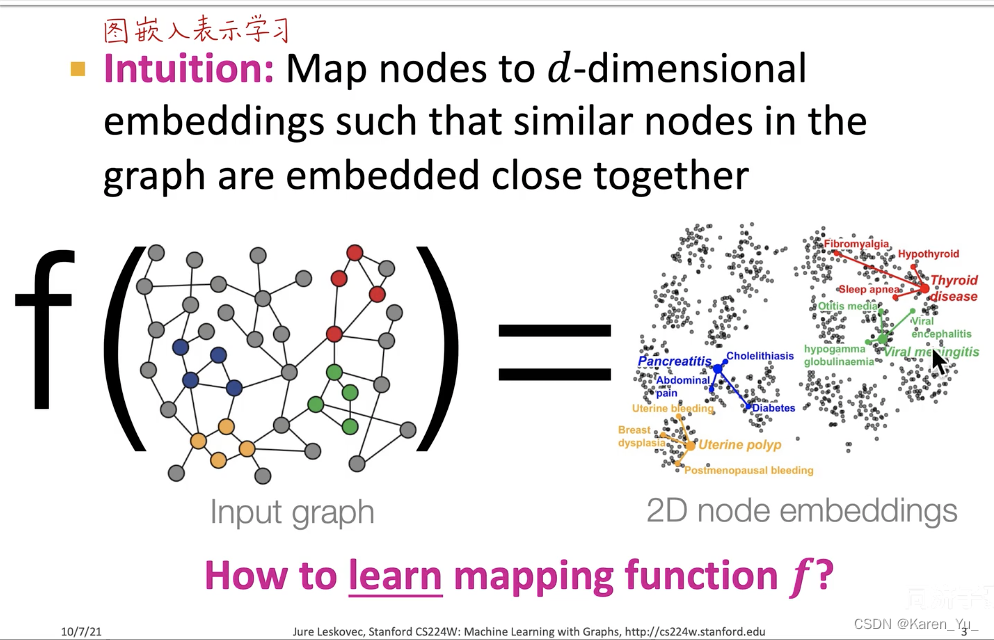
我们要学习的就是这个f函数，我们把图输入给这个函数，会输出每一个节点的embedding（嵌入）。在d维空间的嵌入，向量之间的距离就可以表示节点在原图中的距离和关系。
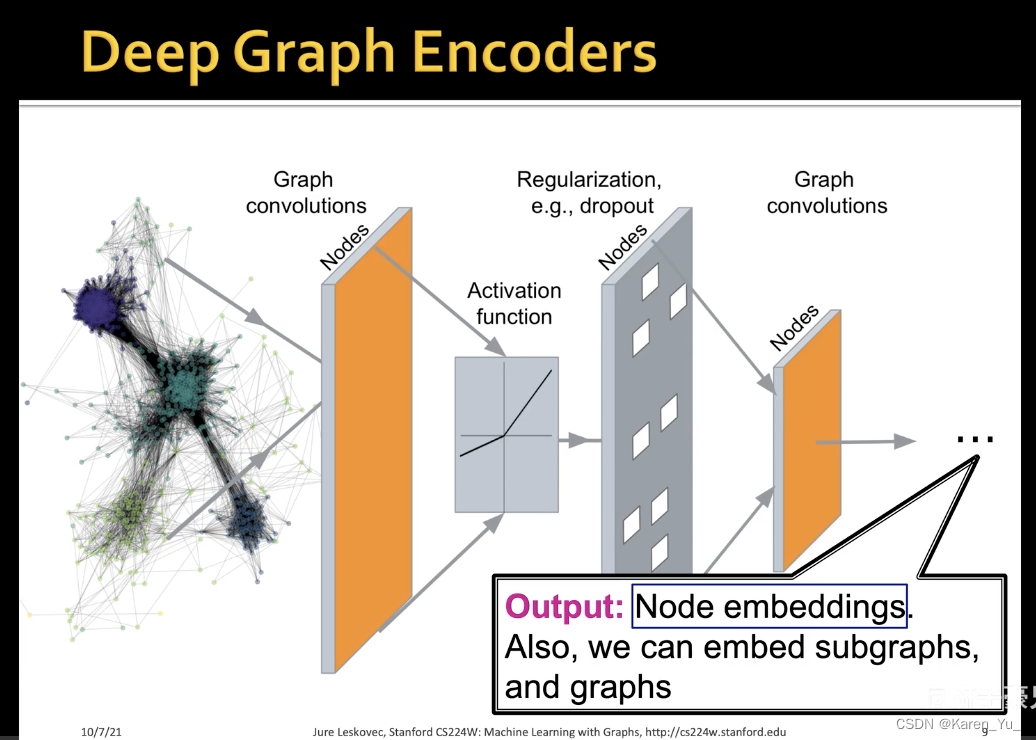
当然，我们也可以获得子图或者整张图的embedding，来解决各种各样的问题（都可以通过节点embedding向量加一个预测头解决，但是前提是这个节点embedding的d维向量的质量要足够高，足够能反映信息和语义）
图卷积神经网络
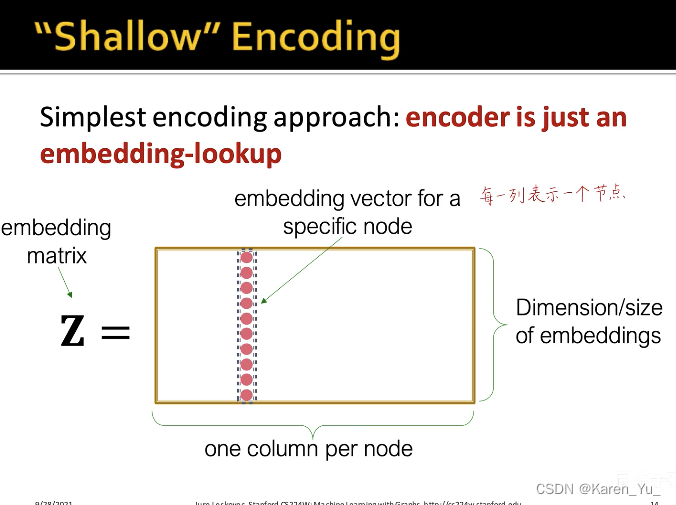
计算图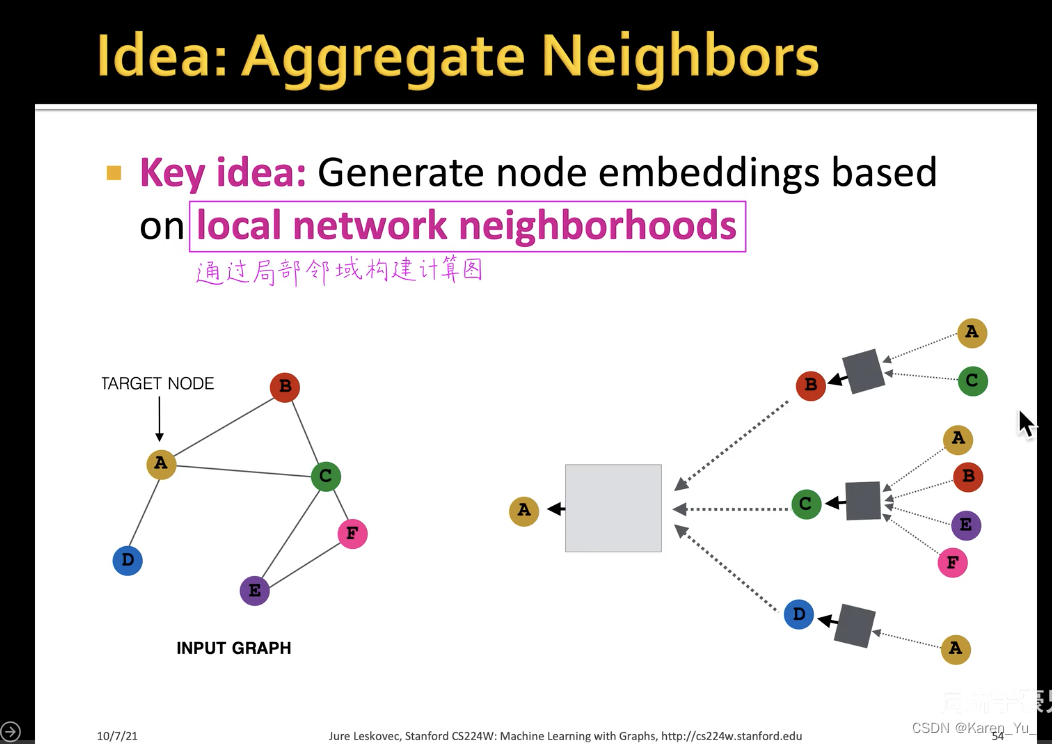
对于图这种没有顺序、参考点而言，我们不能直接把图输入神经网络中，更遑论卷积神经网络了。而是需要通过消息传递的框架去构建局部领域的计算图。
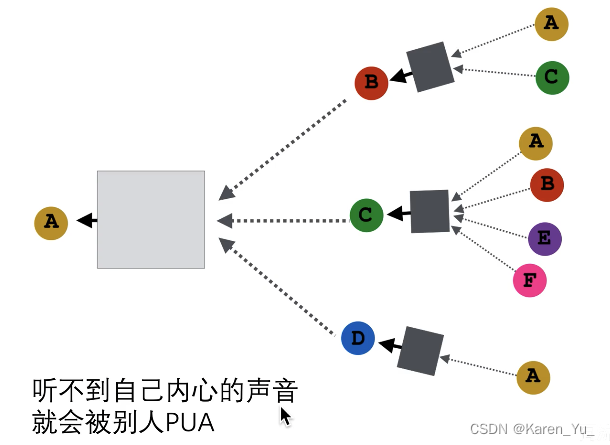
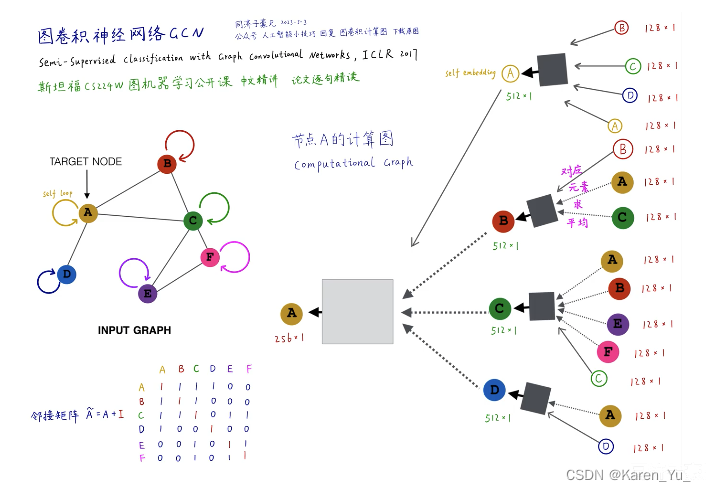
上图左侧为原图，A节点的计算图就是它的一阶邻域（B、C、D三个节点），再看一阶邻域的邻居，B就是A和C，C节点就是ABEF，D就是A。->构建A点的两层神经网络的消息传递的计算图
图中黑色的矩形就是第一层神经网络，灰色的矩形是第二层神经网络->也就是三个黑色矩形共享同一套权重（同一个神经网络）
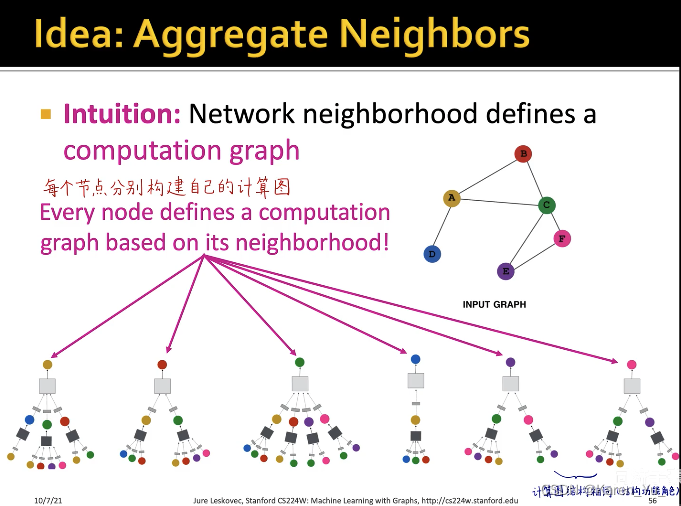
每个节点可以分别构建出自己的计算图，训练图神经网络的时候，每一个计算图就是一个样本->如果batch size=8，那就是8个这样的计算图输入到网络中去
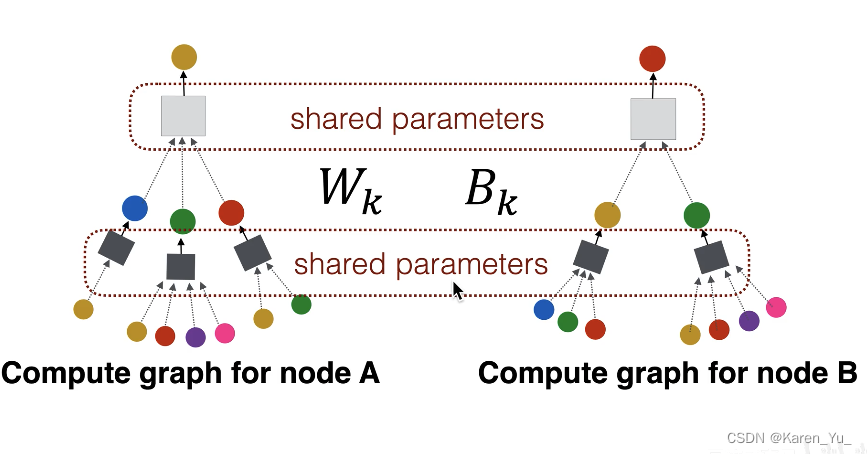
其实，在两层神经网络中只有两个神经网络。
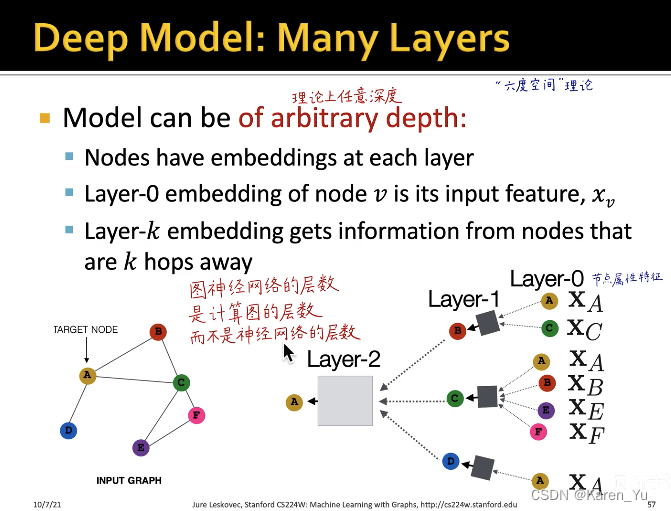
图神经网络的层数并非神经网络的层数，而是指计算图的层数。而这个黑色矩形中具体神经网络的层数可以有很多。
在第0层输入到图神经网络中的是节点的属性特征（样本自带的属性）不需要学习，比如用户的年龄、学历、婚姻状况、收入etc。我们的目标是输入所有节点的属性特征，通过层层的消息传递、信息汇聚，得到这个节点最终的embedding 向量。
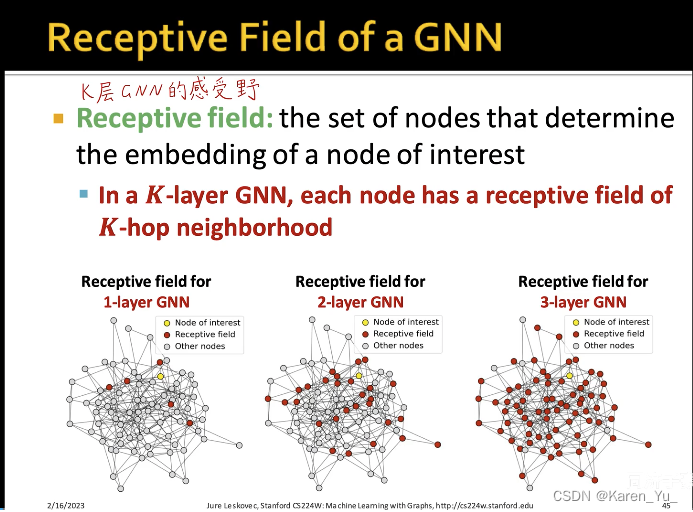
一层神经网络就对应了一个hop的neighborhood，k层就对应了k-hop neighborhood->层数越多，邻居的个数就越多->感受野就越大（覆盖的节点就越大）
不能让图神经网络无限深，if深++，then所有节点的计算图最后都很类似->会产生过平滑（over smoothing）->所有节点的embedding最后都会收敛到同一个值（所有节点的embedding都一样）
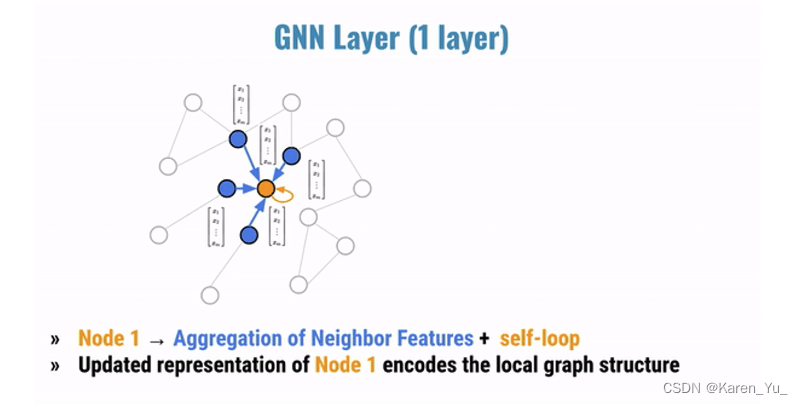
通过层层的消息传递，得到节点最终的embedding
以GCN为例。假设每个节点都有128维的属性特征。计算B节点的embedding，就是A和C两个节点的属性特征逐元素求平均，得到一个新的128维的向量，输入到黑色矩形中，输入128维，输出512维，得到B节点的向量，对于C节点就是四个节点ABEF的属性特征逐元素求平均，输入，得到C节点的向量。D节点就是直接输入A节点的属性（128维的embedding）->GCN的第一层
（弹幕：这里输入大小不同，那不就说明神经网络是不一样的吗？
噢噢，我知道了，是逐元素求平均得到128维，所以神经网络是输入128维，输出512维，共享参数没毛病）
那么第二层就是把BCD这三个512维的向量逐元素的求平均，得到一个新的512维向量，输入白色矩形中，输出一个256维的向量，此向量为A节点最终的embedding，作为A节点的输出。
逐元素求平均与顺序无关（order invariant/permutation invariant），当然不仅仅只能用求平均，也可以采用取最大值、求和等操作。这些操作都与顺序无关。
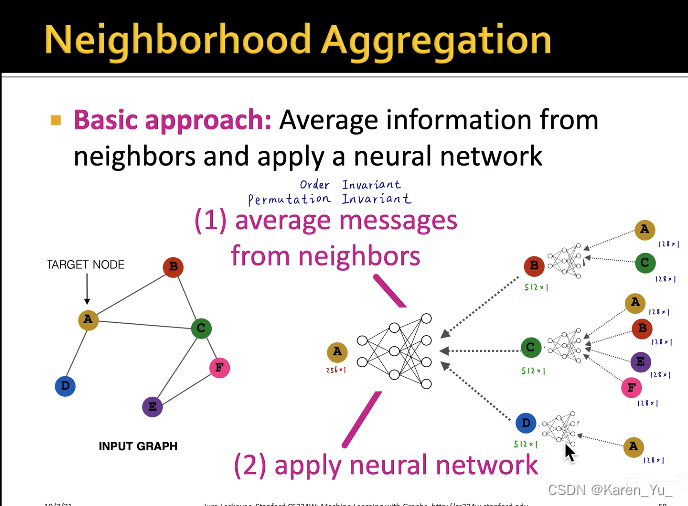
在计算图中的矩形是什么呢？可以是多层感知器、全连接神经网络etc
我们要做的就是训练两个神经网络的权重（白色和黑色矩形）
当我们训练完之后，我们就直接把各个节点的属性特征输入进去，跑一下神经网络，就能得到最终A节点的embedding了。
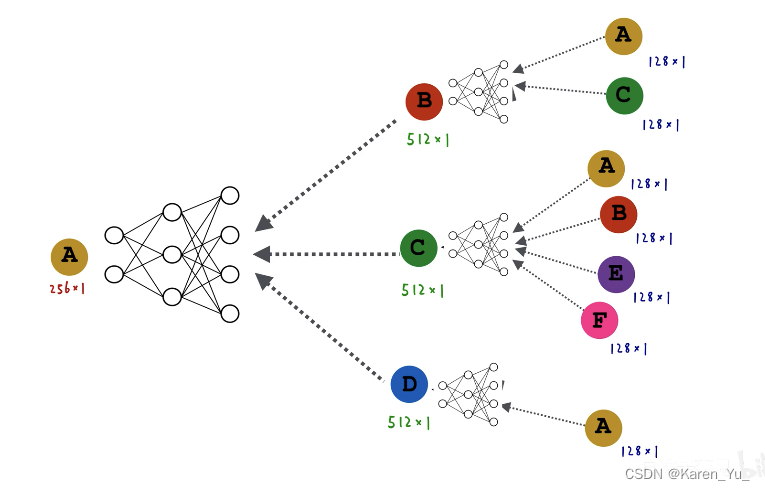
⬆️小结
数学形式
可以调整输入输出神经元的维度（前面的例子128 512 256）
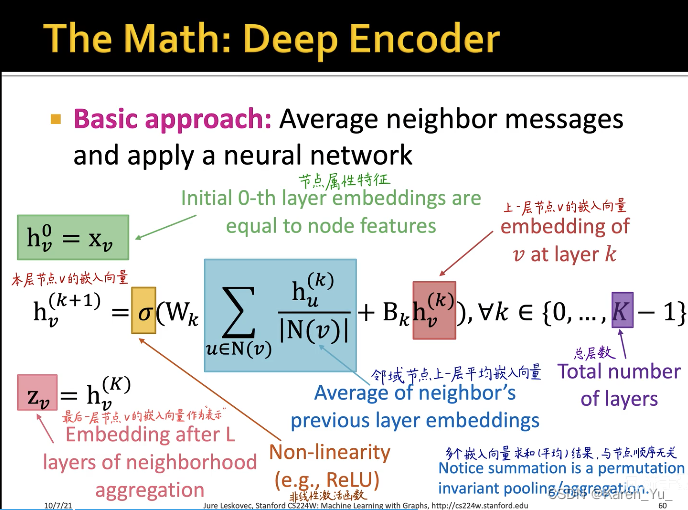
：v节点在第0层的embedding（即属性特征）
如果一个节点没有属性特征，可以强行全部设为1，或者设置成one-hot的形式
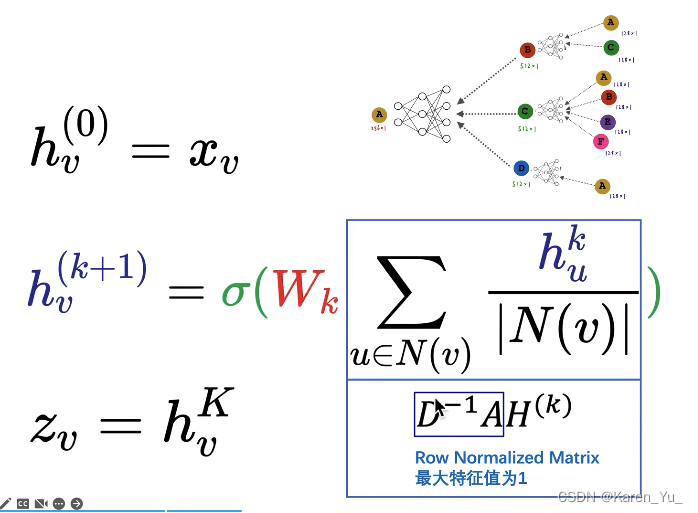
第k+1层，v节点的embedding是由第k层v节点的邻域节点u算出来的。先找到v节点的所有邻居节点，以C节点为例，u就是ABEF四个节点，把k层u的embedding加起来求和，再除以C节点的连接数（4）->就是求平均
将得到的新的向量输入到nn中，再经过一个激活函数->得到k+1层v节点的embedding
：v节点最后输出的embedding。比如图中的例子，这里的K表示总共有几层（这里K=2）
这里，我们将第K层每一个节点的embedding都写成矩阵中的一行，给这个
左乘一个邻接矩阵A的第v行，就相当于把v节点的邻域节点的embedding向量挑出来了。
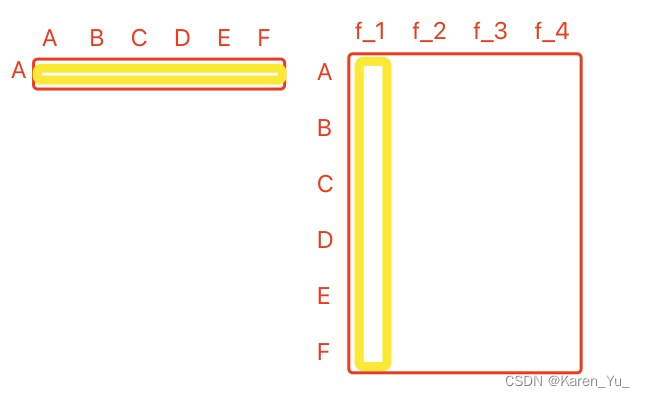
只要邻接矩阵是1（两个节点相连），自然就把对应的特征挑出来了
OK，求和搞定了，下一个就是怎么求平均：
设置矩阵D（度矩阵），是一个对角阵，对D矩阵求逆（就是对角线上的值变成倒数）
求平均
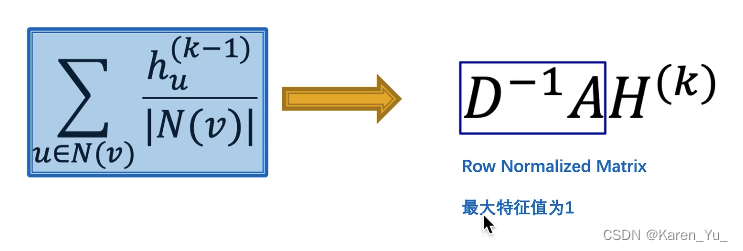
OK，现在我们拿到了矩阵的表示形式
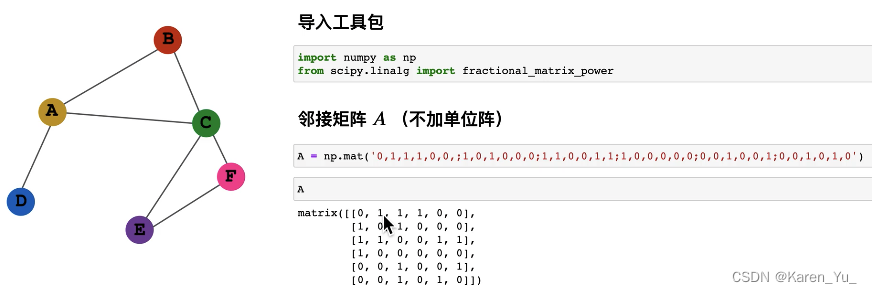
按照这种方式，是暴力求平均，而没有考虑不同的节点的情况，比如这个例子里舔狗D明显纯舔，舔狗C都脚踏不知道多少条船了，当然A感受到的是不一样的。
解释一下这个幅值变小（相当于对向量做线性变换，本来长度是1，在-1到1之间就是长度变短了）
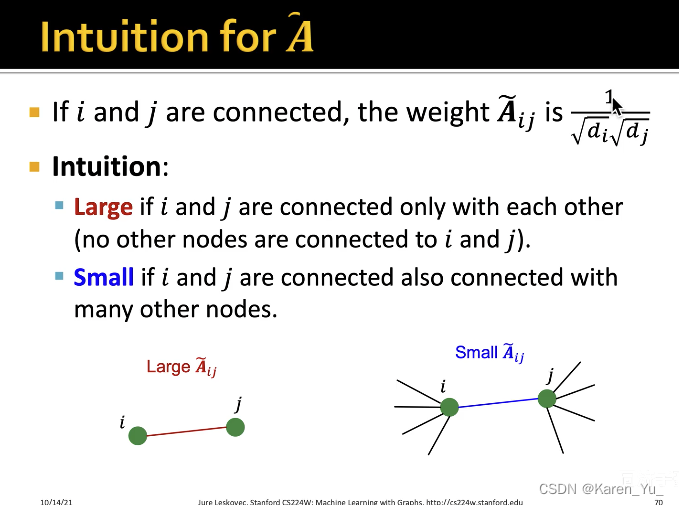
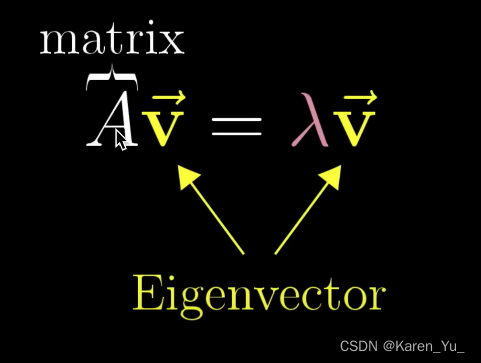
如果一个向量左乘了A矩阵，代表对这个向量进行线性变换，线性变换后向量的方向没变，长度变为原来的倍
OK，现在的数学表示变成：
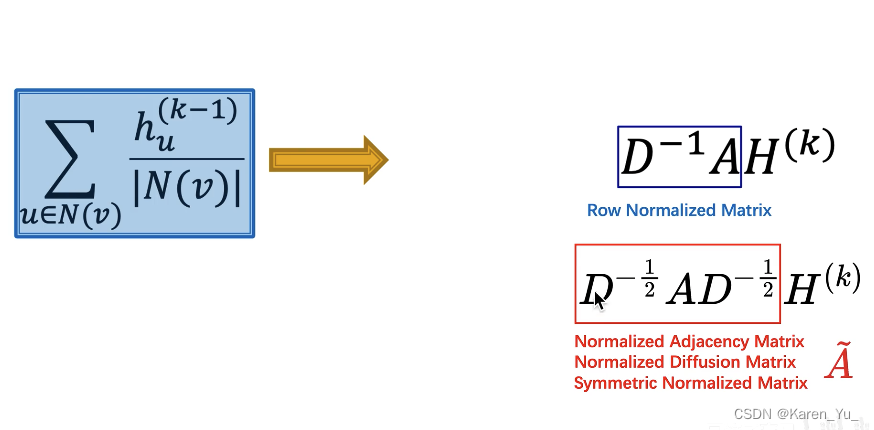
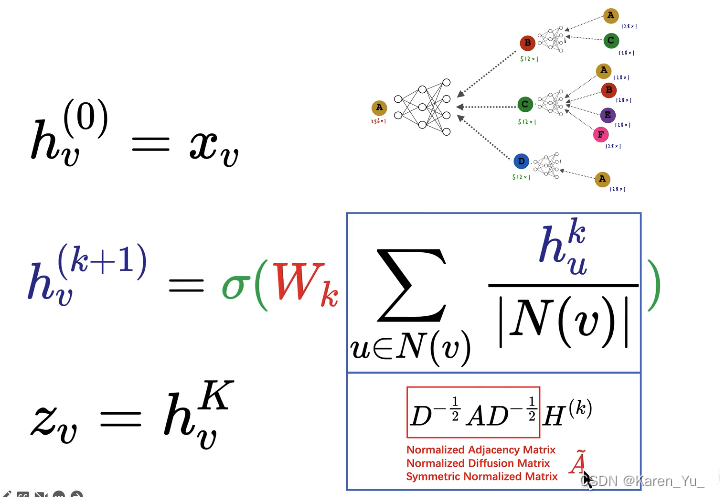
这里可学习的参数是，权重矩阵
改进
那么此时，我们给每个节点都加一个引向自己的连接
进一步扩展，邻域和self embedding使用不同的权重：
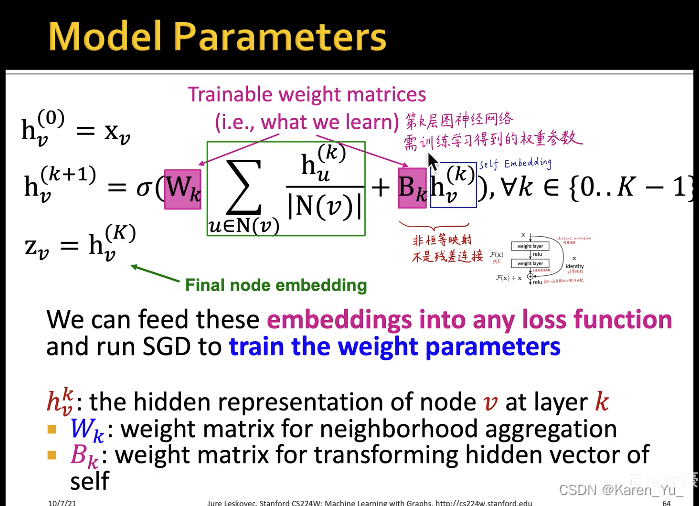
讨论
怎样训练
如果采用监督学习的方式，通过最小化损失函数进行训练（比如交叉熵损失函数）
如果是无监督，使用图自身的结构，类似DeepWalk、Node2Vec，让原图中直接向量的两个点学到的向量更接近。
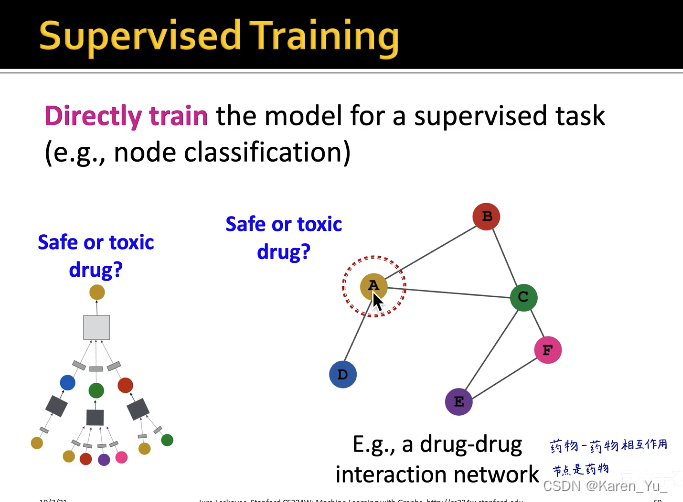
对于无监督，把两个节点分别输入GNN，得到两个d维向量，直接算这两个d维向量的点乘（其实就是余弦相似度）->希望余弦相似度能直接反映两个节点在原图中的关系。->越接近1（大）越好
优点
GNN可以泛化到新节点
直推式学习的缺点
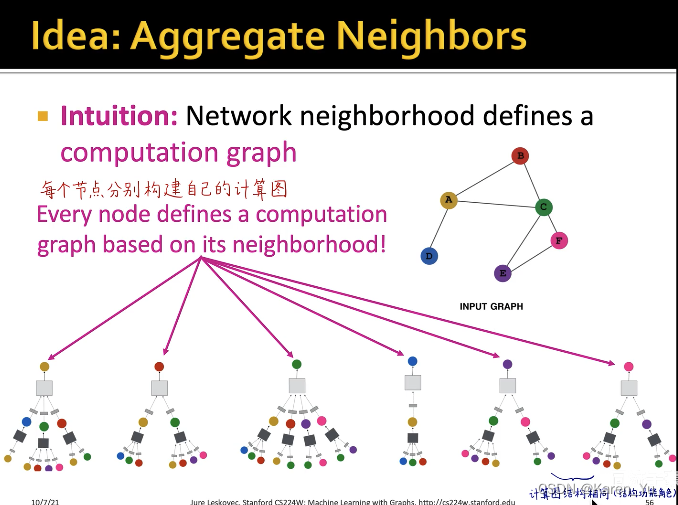
EF节点的计算图像->这两个节点的结构、功能、角色特征相似
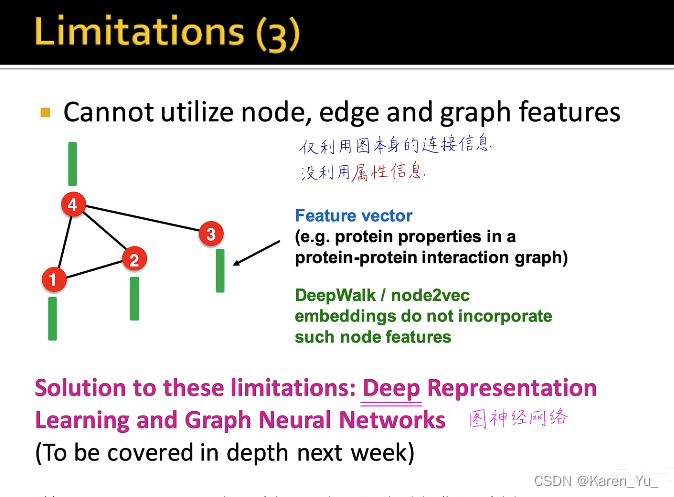
小结：
这些缺点GNN都可以弥补：
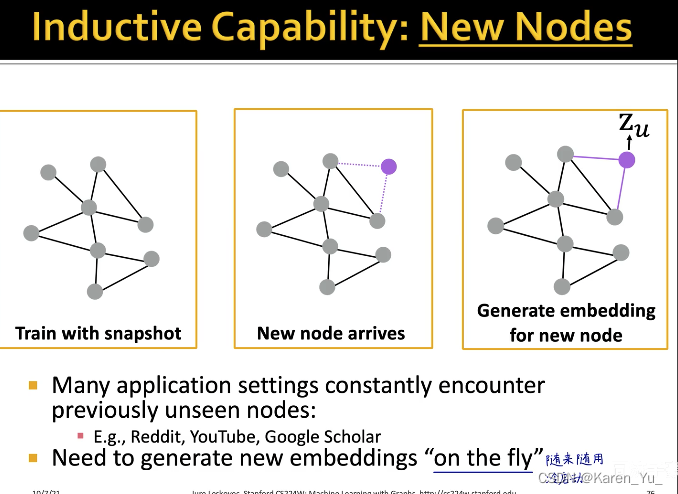
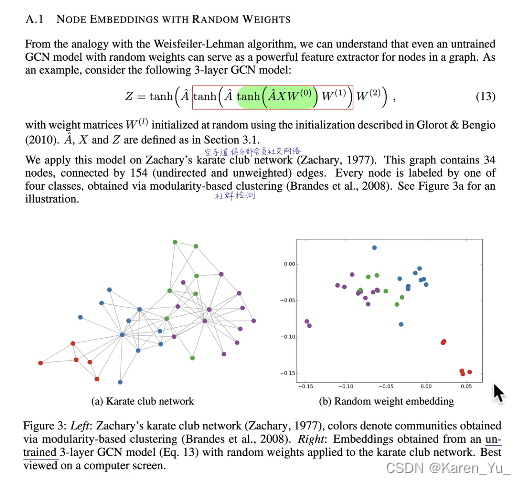
表示能力很赞哦（没有经过训练的nn就可以做到区分）
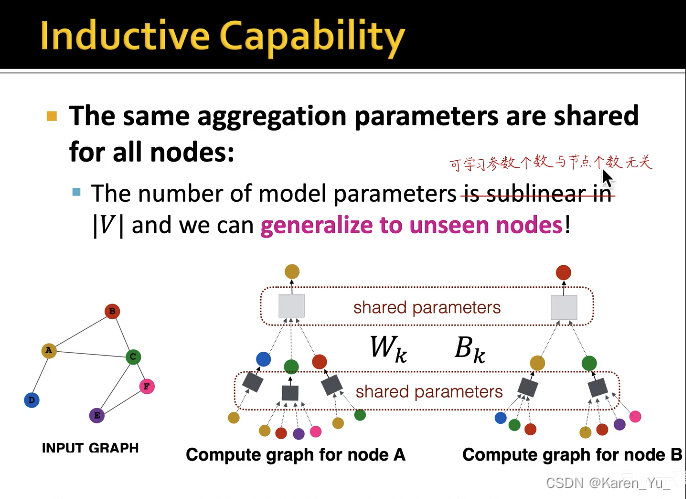
参数是共享的，可学习参数是固定的（参数是共享的）
总结
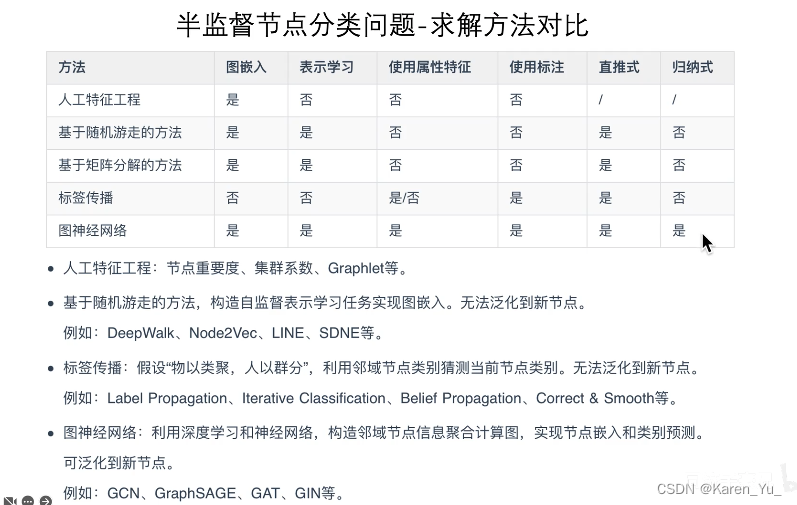
GNN与其他NN的关系
CNN
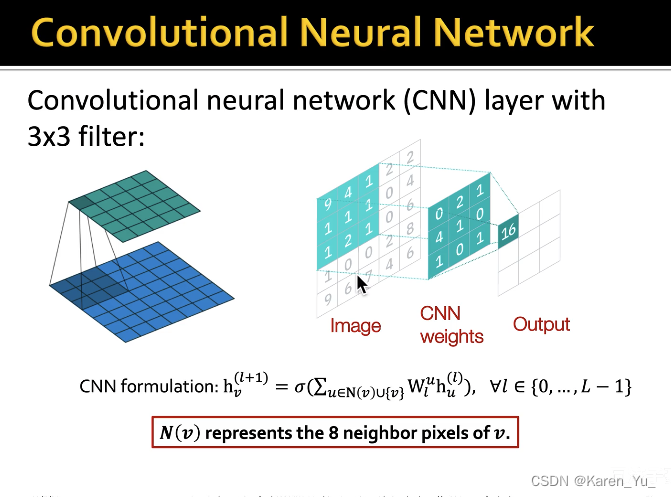
卷积神经网络也可以被看作是一个图神经网络。每个像素都有自己的邻居，比如上图最中间的1有8个邻居，CNN其实就是对这个8-邻域的信息进行汇总
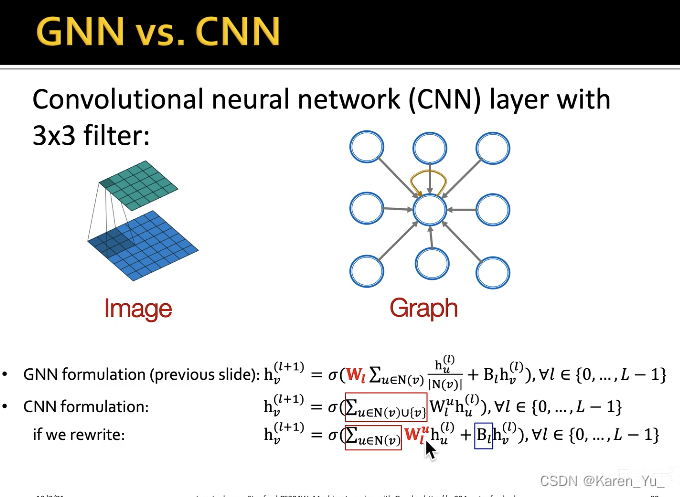
区别在于CNN中，卷积核是需要学习的，但是在GCN中，是由normalized adjacency matrix预定义好的（不用学）
并且CNN不能调换像素位置
Transformer
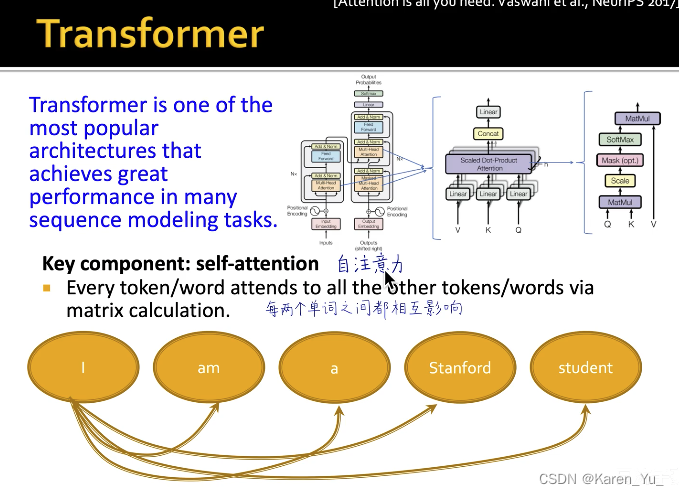transformer的本质是自注意力 ，使得每两个单词之间可以互相影响（可以抽象看作是一个全连接图）
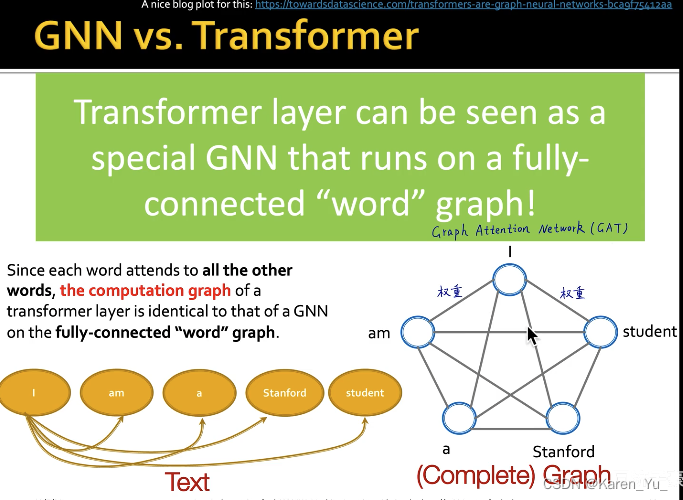
->GAT（这个可以学权重）
这里权重是预先定义好的，不需要学
论文
https://arxiv.org/pdf/1609.02907
看了一下论文内容，前面基本上都cover了，这里略。
深入浅出了解GCN原理（公式+代码）_gcn公式-CSDN博客
![[leetcode] 64. 最小路径和](https://img-blog.csdnimg.cn/direct/a36c1b59f2eb48eebd27dc7ba26116ca.png)
