一、前言
论文: Deformable DETR: Deformable Transformers for End-to-End Object Detection
作者: SenseTime Research
代码: Deformable DETR
特点: 提出多尺度可变形注意力 (Multi-scale Deformable Attention) 解决DETR收敛速度慢、特征图尺度单一等问题。
二、框架
下图为DETR(左)和Deformable DETR(右)的结构图:
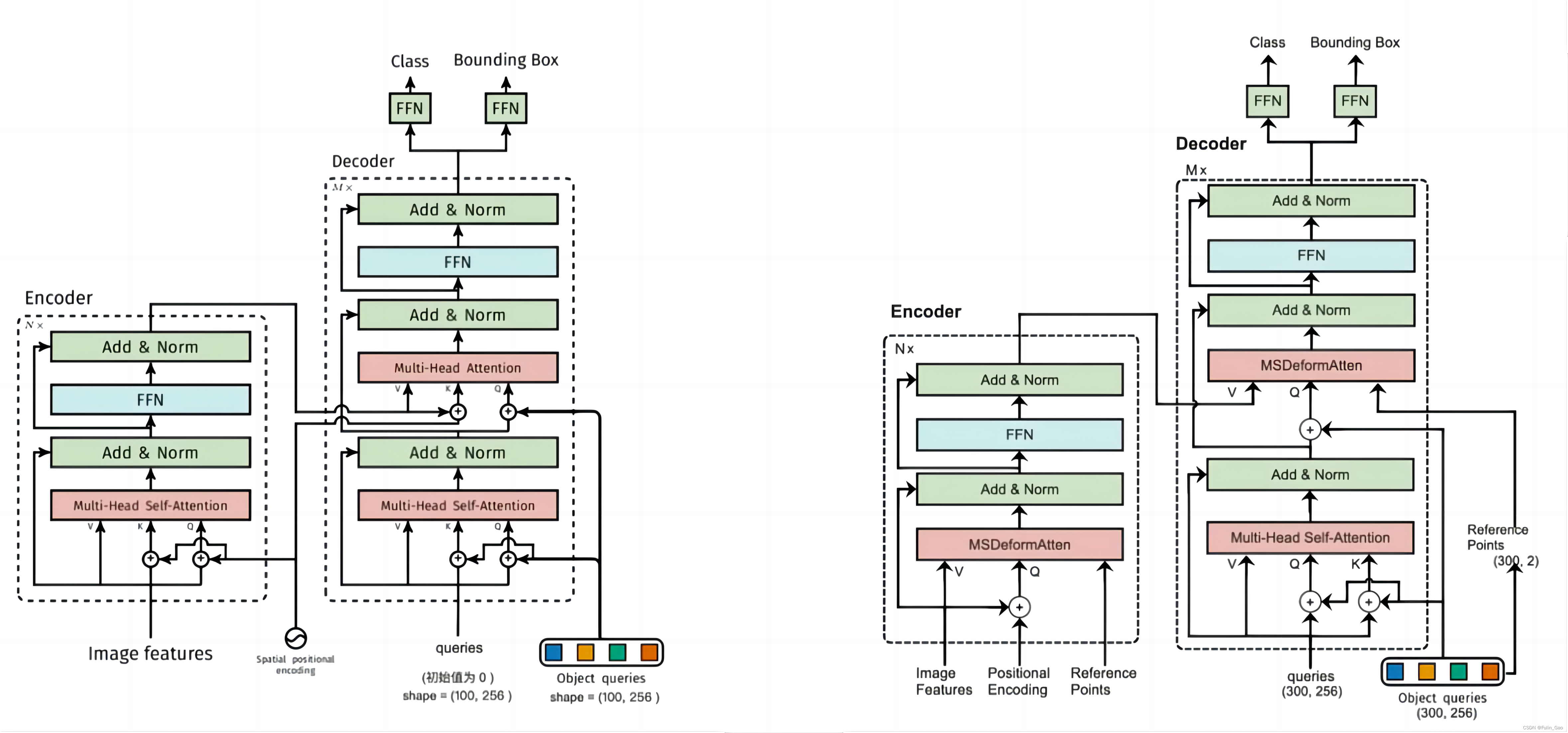
可见,二者的总体结构类似,主要区别在于注意力模块和相应的输入不同。所以,我们按照之前介绍DETR时的顺序依次介绍Deformable DETR与DETR在Backbone、Encoder、Decoder、Prediction Heads中的不同之处。
1. Backbone
保留尺寸小的特征图有利于检测大目标,保留尺寸大的特征图善于检测小目标。 为此,Deformable DETR提取4个尺寸下的特征图(DETR仅1个尺寸),特征提取过程如下图:
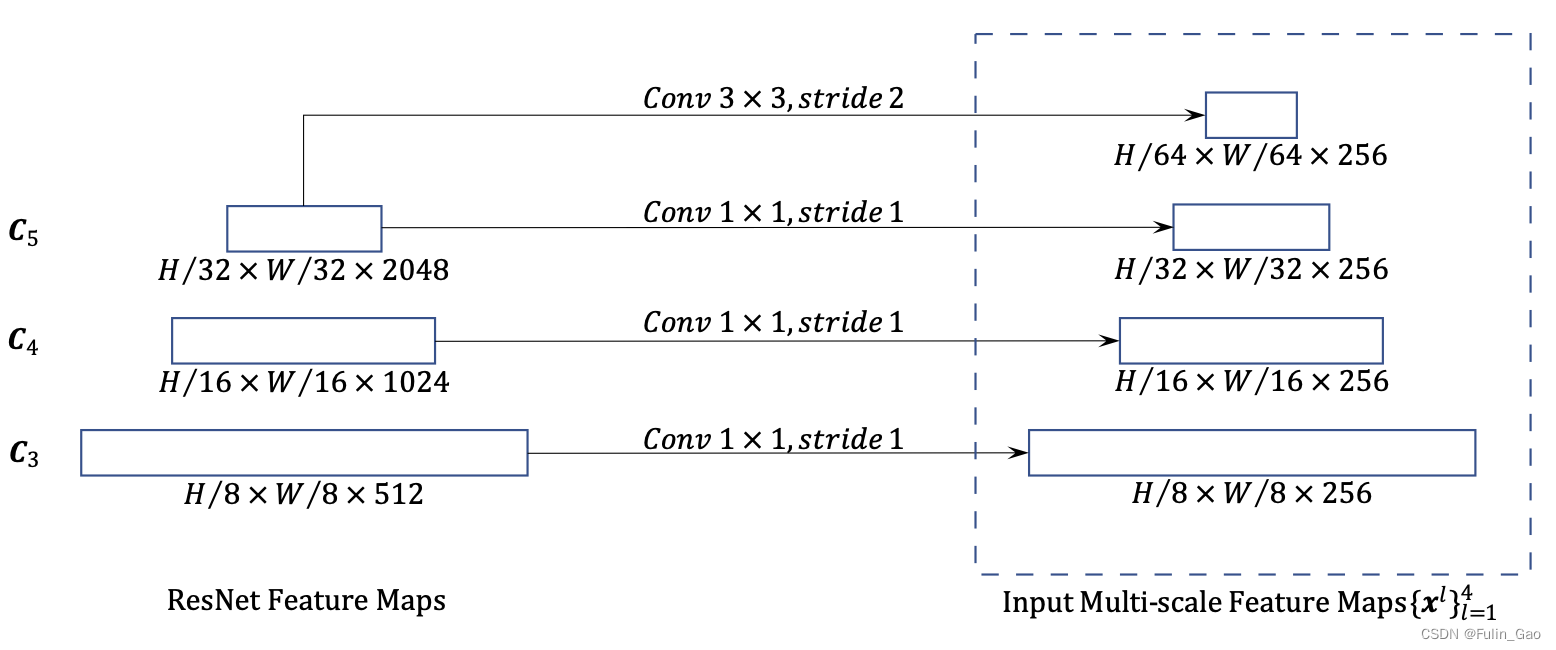
首先,Deformable DETR通过ResNet-50输出3个尺寸的特征图,分别为原图高宽的 1 8 \frac{1}{8} 81、 1 16 \frac{1}{16} 161、 1 32 \frac{1}{32} 321。3个特征图后接核为 1 ∗ 1 1*1 1∗1、步长为1的卷积层统一通道数为256。其次,在最后一层 1 32 \frac{1}{32} 321的特征图后跟一个核为3*3、步长为2的卷积层实现降采样和通道数统一,得到1个原图高宽 1 64 \frac{1}{64} 641通道数为256的特征图。于是共得到4个不同尺寸下( 1 8 \frac{1}{8} 81、 1 16 \frac{1}{16} 161、 1 32 \frac{1}{32} 321、 1 64 \frac{1}{64} 641)通道数均为256的特征图。
每个用于统一通道数的卷积层后都跟了一个GroupNorm层,Group的大小(32)与token向量长度(256)和多头注意力的头数(8)有关( 32 = 256 ÷ 8 32=256\div 8 32=256÷8)。此外,每个特征图都有对应的mask(表示padding情况,同一批次的图像尺寸会被统一以方便计算)和位置编码(与DETR中的Spatial positional encoding相同)。
不过,Spatial positional encoding无法区分不同层同一像素位置的位置编码向量,即小的特征图的位置编码是大的特征图的位置编码的子集。例如,第一个特征图在(2,4)像素点上的位置编码向量与另外三个特征图在(2,4)像素点上位置编码向量是相同的;只是大的特征图的位置编码向量数量更多,第一个特征图有(70,100)这个像素点,但其他特征图可能没有这个像素点。为此,Deformable DETR为不同特征图的位置编码加上了不同的可学习参数(nn.Parameter(特征图数量, 256)),同一特征图的所有像素点的位置编码加上的参数是相同的。
2. Encoder
Deformable DETR与DETR在Encoder部分的主要区别在下图的左下角部分:
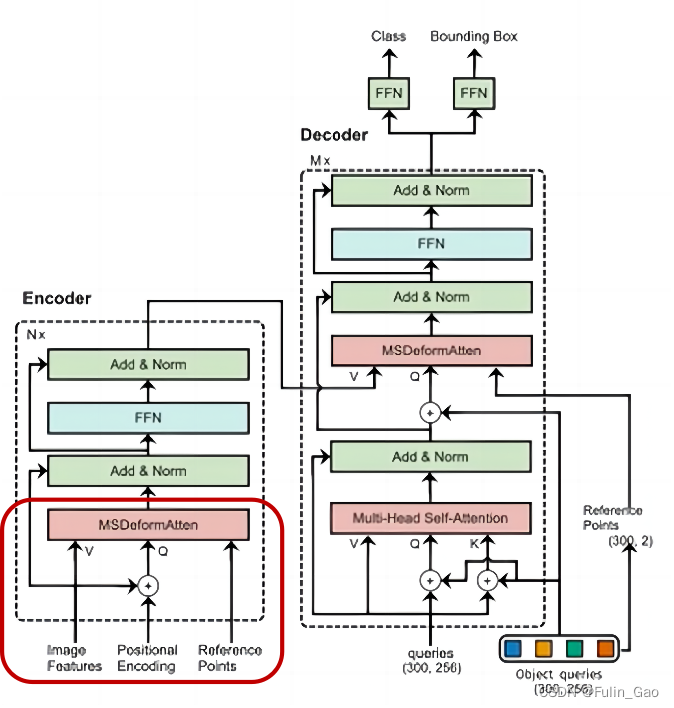
其中,Image Features为Backbone输出的4个不同尺寸下的特征图;Positional Encoding为各特征图的Spatial positional encoding+各自的可学习参数;Reference Points为各个特征图像素点的归一化坐标。
2.1 参考点
Deformable DETR的注意力模块需要参考点 (Reference Points) 作为基准来定位用于加权的像素点。注意力我们在后面讲,这里先理解参考点。
之前我们说参考点是各个特征图像素点的归一化坐标,其实不完全正确。一般来说,每个特征图都有且只有自己的像素点(如下图左侧两个子图):
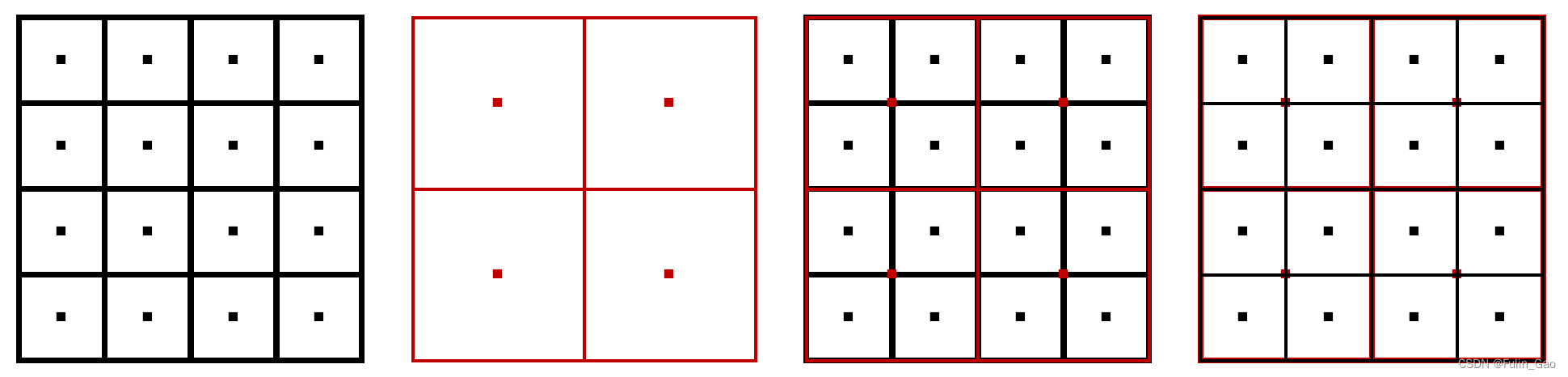
Deformable DETR用 (x,y) 表达各特征图的像素点。x和y均从0.5开始,分别从宽-0.5和高-0.5结束。具体来说,第一个特征图,宽为4,则各列x的坐标为 0.5 , 1.5 , 2.5 , 3.5 0.5,1.5,2.5,3.5 0.5,1.5,2.5,3.5,高为4,则各行y的坐标为 0.5 , 1.5 , 2.5 , 3.5 0.5,1.5,2.5,3.5 0.5,1.5,2.5,3.5;第二个特征图,宽为2,则各列x的坐标为 0.5 , 1.5 0.5,1.5 0.5,1.5,高为2,则各行y的坐标为 0.5 , 1.5 0.5,1.5 0.5,1.5。
为了增加像素点的数量,Deformable DETR将各个特征图的像素点坐标映射到了其它特征图上(如上图右侧两个子图)。映射前需要通过 (x/宽,y/高) 将不同特征图下单像素点坐标归一化(如果不归一化,小的特征图能映射到大的特征图上,但大的特征图无法映射到小的特征图上)。
原本4个尺度下的特征图共有 h e i g h t / 64 ∗ w i d t h / 64 + h e i g h t / 32 ∗ w i d t h / 32 + h e i g h t / 16 ∗ w i d t h / 16 + h e i g h t / 8 ∗ w i d t h / 8 height/64*width/64+height/32*width/32+height/16*width/16+height/8*width/8 height/64∗width/64+height/32∗width/32+height/16∗width/16+height/8∗width/8 个像素点,归一化+映射后每个特征图都有这么多个像素点。所以,参考点是各个特征图本身的像素点和其它特征图映射至此的像素点的归一化坐标。
2.2 注意力
要理解多尺度可变形自注意力,我们需要从单尺度的单头自注意力、多头自注意力、可变形多头自注意力逐步深入。
2.2.1 单尺度多头自注意力
我们熟悉的单尺度单头自注意力公式如下:

其中, Q , K , V Q,K,V Q,K,V是 x \boldsymbol{x} x经不同的全连接层得到的映射, d k d_k dk是 K K K的维度。
单尺度多头自注意力就是将单头的 Q , K , V Q,K,V Q,K,V平均拆分,然后分别执行单头自注意力(详情请参考之前的博客Attention、Self-Attention、Multi-Head Self-Attention)。
Deformable DETR中的单尺度多头自注意力的公式如下:

该公式仅表达 x \boldsymbol{x} x中一个像素点 z q \boldsymbol{z}_q zq的注意力计算过程。其中, x \boldsymbol{x} x是一张图像的全部token; z = x \boldsymbol{z}=\boldsymbol{x} z=x表示 x \boldsymbol{x} x的查询状态, z q \boldsymbol{z}_q zq表示 z \boldsymbol{z} z中的第 q q q个token( z \boldsymbol{z} z加上位置编码后形成 Q Q Q); W ′ x \boldsymbol{W}^{\prime}\boldsymbol{x} W′x表示经全连接映射后的 V V V, W m ′ x \boldsymbol{W}^{\prime}_m\boldsymbol{x} Wm′x表示将 V V V拆分为多头后的第 m m m个头, W m ′ x k \boldsymbol{W}^{\prime}_m\boldsymbol{x}_k Wm′xk表示 V V V的第 m m m个头中的第 k k k个token; A A A表示注意力权重,对应 softmax ( Q K T d k ) \text{softmax}(\frac{QK^T}{\sqrt{d_k}}) softmax(dkQKT)(这里不需要计算,而是通过全连接层映射 Q Q Q得到的), A m q k A_{mqk} Amqk表示对 z q \boldsymbol{z}_q zq执行注意力时,学习到的第 m m m个头中第 k k k个token的注意力权重; ∑ k ∈ Ω k \sum_{k\in\Omega_k} ∑k∈Ωk表示需要对所有token进行加权才能得到 z q \boldsymbol{z}_q zq的对应输出; ∑ m = 1 M W m \sum_{m=1}^{M}\boldsymbol{W}_m ∑m=1MWm表示将各头输出拼接后做一次全连接映射(其实这种表述与公式并不对应,但与源码对应,公式表示先映射后相加,但源码中是先拼接后映射)。
总结下来,Deformable DETR的单尺度多头自注意力与常规单尺度多头自注意力有如下不同:
(1)
Q
Q
Q未经全连接映射,也没有
K
K
K。
(2) 注意力权重不是计算得来,而是经全连接层映射
Q
Q
Q得到的。
此时,Deformable DETR将原本的 softmax ( Q K T d k ) \text{softmax}(\frac{QK^T}{\sqrt{d_k}}) softmax(dkQKT)替换成了全连接,已经降低了计算复杂度。
2.2.2 单尺度可变形多头自注意力
为了进一步降低复杂度,Deformable DETR引入可变形概念。直白来说,上面对 z q \boldsymbol{z}_q zq执行注意力时需要加权所有token(如下图有 10 × 10 10\times 10 10×10个),引入可变形概念后只需要加权 K K K个token(下图中 K = 3 K=3 K=3, 3 ≪ 10 × 10 3\ll 10\times 10 3≪10×10)。

Deformable DETR中单尺度可变形多头自注意力的公式如下:
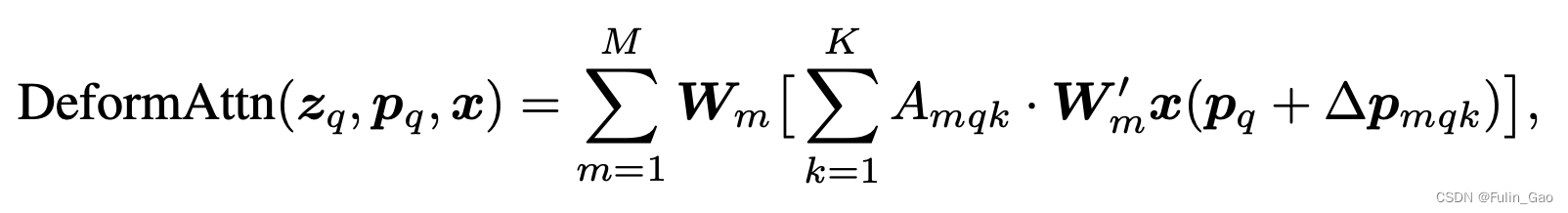
其中, p q \boldsymbol{p}_q pq表示 z q \boldsymbol{z}_q zq的坐标(不需要归一化); Δ p m q k \Delta\boldsymbol{p}_{mqk} Δpmqk是 z q \boldsymbol{z}_q zq经全连接学习到的坐标偏移量; W m ′ x ( p q + Δ p m q k ) \boldsymbol{W}^{\prime}_m\boldsymbol{x}(\boldsymbol{p}_q+\Delta\boldsymbol{p}_{mqk}) Wm′x(pq+Δpmqk)就是在 V V V的第 m m m个头上坐标位置为 p q + Δ p m q k \boldsymbol{p}_q+\Delta\boldsymbol{p}_{mqk} pq+Δpmqk的token。
与单尺度多头自注意力对比可知,有以下不同:
(1)
∑
k
∈
Ω
k
\sum_{k\in\Omega_k}
∑k∈Ωk变成了
∑
k
=
1
K
\sum_{k=1}^{K}
∑k=1K。与
z
q
\boldsymbol{z}_q
zq相关的注意力仅需加权
K
K
K个token,而不再是
∣
Ω
k
∣
=
H
×
W
|\Omega_k|=H\times W
∣Ωk∣=H×W个。
(2)
x
k
\boldsymbol{x}_k
xk变成了
x
(
p
q
+
Δ
p
m
q
k
)
\boldsymbol{x}(\boldsymbol{p}_q+\Delta\boldsymbol{p}_{mqk})
x(pq+Δpmqk)。
p
q
\boldsymbol{p}_q
pq位置的像素点有确定的token,但
Δ
p
m
q
k
\Delta\boldsymbol{p}_{mqk}
Δpmqk是浮点型的,
p
q
+
Δ
p
m
q
k
\boldsymbol{p}_q+\Delta\boldsymbol{p}_{mqk}
pq+Δpmqk位置的像素点可能无明确的token,Deformable DETR中使用双线性插值计算对应token。
为帮助理解,我们看下图(该图为单尺度可变形单头自注意力的部分流程):
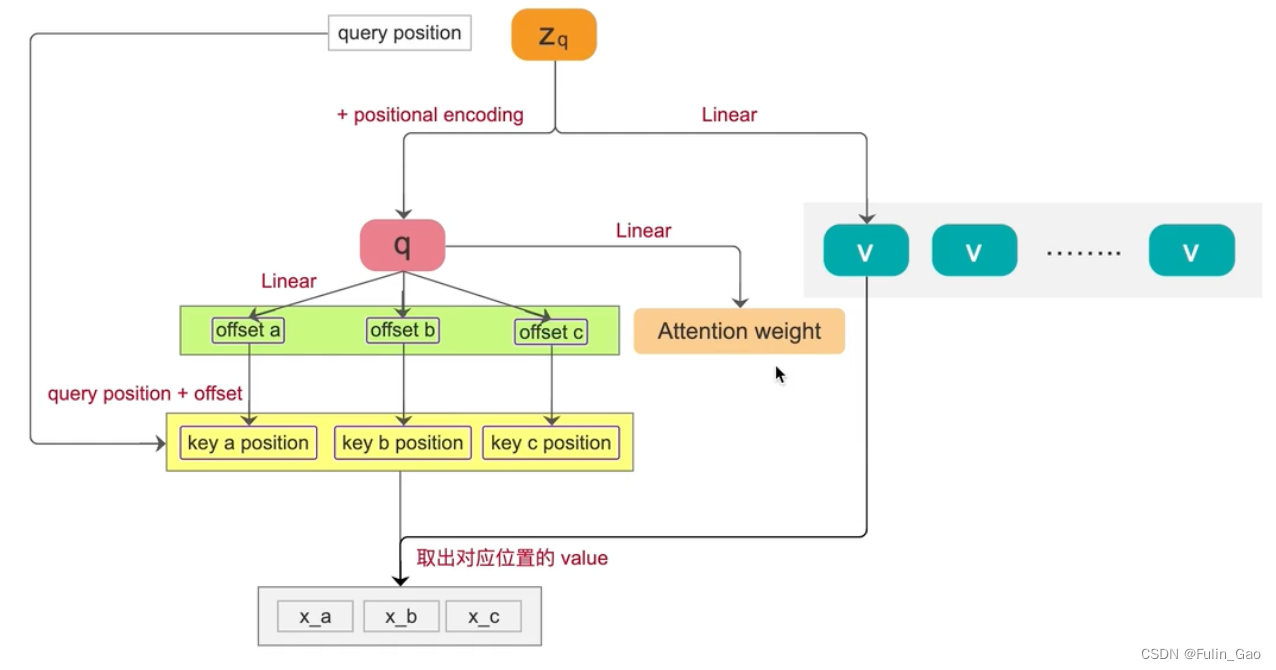
z q \boldsymbol{z}_q zq加上位置编码形成q( z \boldsymbol{z} z加上位置编码形成 Q Q Q); z q \boldsymbol{z}_q zq经全连接线性映射形成v( z \boldsymbol{z} z经全连接线性映射形成 V V V);q经全连接线性映射得到坐标偏移量, z q \boldsymbol{z}_q zq的参考点坐标加上坐标偏移量得到用于加权的token的坐标,从 V V V中经双线性插值可以取出对应坐标的token;q经全连接线性映射得到注意力权重,将权重乘在取出的token上求和即可得到与 z q \boldsymbol{z}_q zq对应的注意力输出。多头则是将q拆分后再分别经全连接映射得到坐标偏移量和注意力权重以及后续各个操作,最后将各头输出拼接再经全连接映射获得最终输出。
此时,Deformable DETR选取 K K K个token做加权进一步降低了计算复杂度,模型已经能够接受大尺度的特征图。
2.2.3 多尺度可变形多头自注意力
为提升小目标检测能力,Deformable DETR引入了多尺度特征图。
Deformable DETR中多尺度可变形多头自注意力的公式如下:
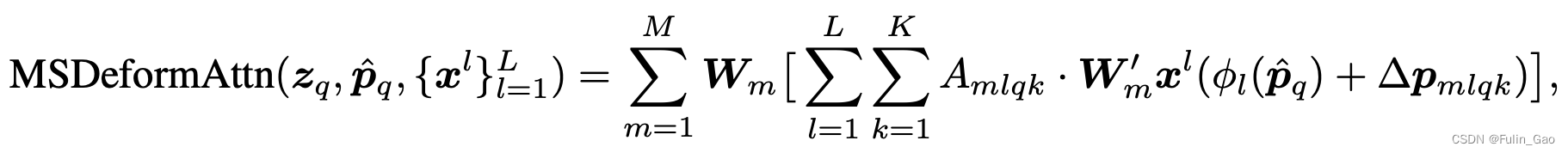
其中, p ^ q \hat{\boldsymbol{p}}_q p^q表示归一化后的坐标(就是上面提到的参考点); { x l } l = 1 L \{x^l\}_{l=1}^L {xl}l=1L表示 L L L个特征图输入(原文中 L = 4 L=4 L=4); ϕ l ( p ^ q ) \phi_{l}(\hat{\boldsymbol{p}}_q) ϕl(p^q)表示将 p ^ q \hat{\boldsymbol{p}}_q p^q映射为归一化前的坐标。
与单尺度可变形多头自注意力对比可知,有以下不同:
(1) 增加了输入特征图数量。尺寸小的特征图善于检测大目标,尺寸大的特征图善于检测小目标。
(2) 增加了单个特征图的像素点数量(在公式中没有体现)。在产生参考点时,每个特征图除自身像素点外还扩充了其它特征图的像素点,所以执行注意力的
z
q
\boldsymbol{z}_q
zq数量也增加了。
(3) 增加了坐标的映射
ϕ
l
(
⋅
)
\phi_{l}(\cdot)
ϕl(⋅)。将特征图的像素点扩充到其它特征图上需要将坐标归一化后才方便进行,所以需要先归一化再映射回原图坐标。
3. Decoder
Deformable DETR与DETR在Decoder部分的主要区别在下图的右侧两个部分:
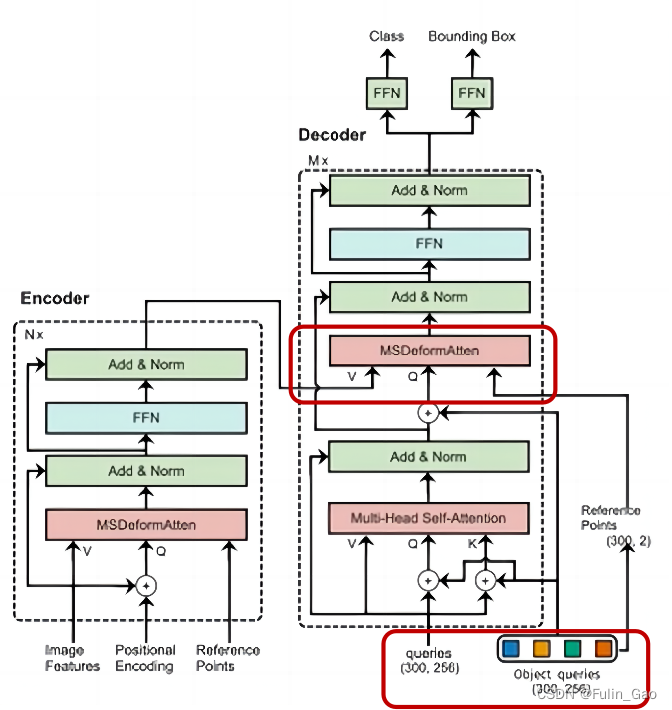
可见,区别在于Decoder的输入、注意力模块及其输入。
对于Decoder的输入部分,详情如下:
(1) Deformable DETR的Decoder可检测目标最大数量变为300(DETR中为100)。
(2) queries和位置编码由nn.Embedding(300, 256)随机初始化(DETR中queries初始化为0)。
(3) 参考点由随机初始化的位置编码经全连接+Sigmoid映射得到。
对于注意力模块及其输入部分,详情如下:
(1) Deformable DETR采用多尺度可变形多头交叉注意力(DETR中为单尺度多头交叉注意力)。
(2)
V
V
V由Encoder提供,
Q
Q
Q为queries经多头自注意力后的输出加上位置编码,参考点为位置编码经全连接+Sigmoid的输出。
4. Prediction Heads
与DETR一样预测目标类别和框坐标,不过目标数上限从100提升至300。
致谢:
本博客仅做记录使用,无任何商业用途,参考内容如下:
Deformable DETR | 1、Abstract 算法概述
Deformable DETR 论文+源码解读
DeformableDetr算法解读