LearnOpenGL（七）之摄像机

news2024/9/22 10:16:00

一、摄像机/观察空间

当我们讨论摄像机/观察空间(Camera/View Space)的时候，是在讨论以摄像机（人）的视角作为场景原点时场景中所有的顶点坐标：观察矩阵把所有的世界坐标变换为相对于摄像机位置与方向的观察坐标。要定义一个摄像机，我们需要它在世界空间中的位置、观察的方向、一个指向它右侧的向量以及一个指向它上方的向量。

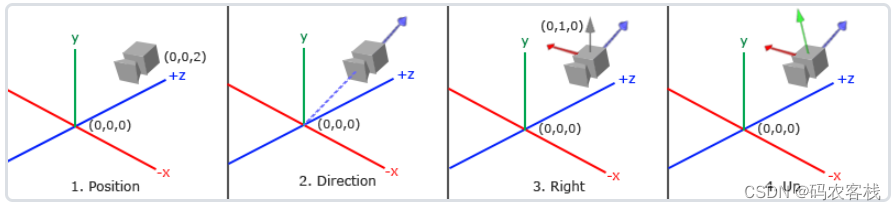
1. 摄像机位置

摄像机位置简单来说就是世界空间中一个指向摄像机位置的向量：

glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f);

2. 摄像机方向

用场景原点向量减去摄像机位置向量的结果就是摄像机的指向向量。由于我们知道摄像机指向z轴负方向，但我们希望方向向量(Direction Vector)指向摄像机的z轴正方向。如果我们交换相减的顺序，我们就会获得一个指向摄像机正z轴方向的向量：

glm::vec3 cameraTarget = glm::vec3(0.0f, 0.0f, 0.0f);
glm::vec3 cameraDirection = glm::normalize(cameraPos - cameraTarget);

3. 右向量

右向量(Right Vector)，它代表摄像机空间的x轴的正方向。

为获取右向量，可以先定义一个上向量，接下来把上向量和第二步得到的方向向量进行叉乘。两个向量叉乘的结果会同时垂直于两向量，因此我们会得到指向x轴正方向的那个向量：

glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f); 
glm::vec3 cameraRight = glm::normalize(glm::cross(up, cameraDirection));

4. 上向量

把右向量和方向向量进行叉乘就可以获取一个指向摄像机的正y轴向量：

glm::vec3 cameraUp = glm::cross(cameraDirection, cameraRight);

5、观察矩阵

观察矩阵需要一个位置、目标和上向量，如下：

glm::mat4 view;
view = glm::lookAt(glm::vec3(0.0f, 0.0f, 3.0f), 
           glm::vec3(0.0f, 0.0f, 0.0f), 
           glm::vec3(0.0f, 1.0f, 0.0f));

二、视角移动

1、欧拉角

欧拉角(Euler Angle)是可以表示3D空间中任何旋转的3个值。

一共有3种欧拉角：俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll)，如下图：

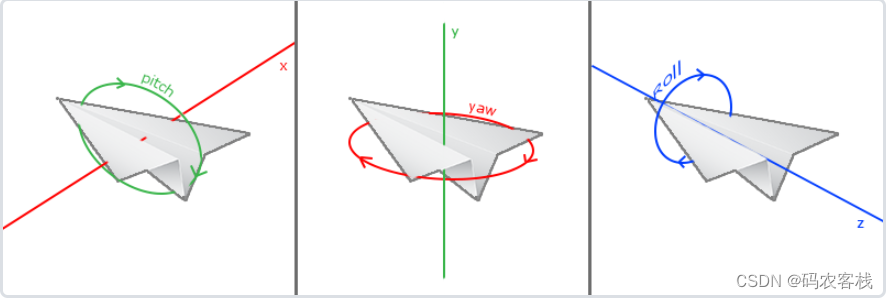
从俯仰角得到的分量：

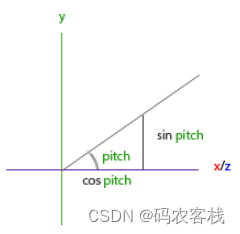
direction.y = sin(glm::radians(pitch)); // 注意先把角度转为弧度
direction.x = cos(glm::radians(pitch));
direction.z = cos(glm::radians(pitch));

从偏航角得到的分量：

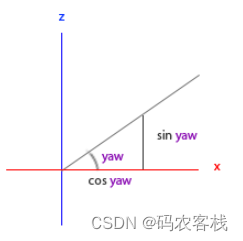
direction.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw)); // direction代表摄像机的前轴(Front)
direction.y = sin(glm::radians(pitch));
direction.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));

通过以上两步，可以把俯仰角和偏航角转化为用来自由旋转视角的摄像机的3维方向向量了（很少会倒转摄像机，暂不讨论）。

demo下载：点击跳转

效果如下：