A. Maximize?
Problem - A - Codeforces
给定x求出使这个式子最大的y:
不用想复杂直接循环枚举即可。
#include<bits/stdc++.h>
using ll=long long;
ll n,m;
void solve()
{
int x;
std::cin>>x;
ll ans=0,y;
for(int i=1;i<x;i++)
{
if(std::__gcd(i,x)+i>ans){
ans=std::__gcd(i,x)+i;
y=i;
}
}
std::cout<<y<<'\n';
}
signed main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t=1;
std::cin>>t;
while(t--)
{
solve();
}
return 0;
}B. Prefiquence
Problem - B - Codeforces
看了一会感觉是二分4min就过了,感觉之前在洛谷刷二分还是蛮大作用的,从只会板子到看得出用得上。
#include<bits/stdc++.h>
using ll=long long;
ll n,m;
std::string a,b;
bool check(int x)
{
int l=0;
for(int i=0;i<m;i++)
{
if(b[i]==a[l])
{
l++;
if(l>=x) return 1;
}
}
return 0;
}
void solve()
{
std::cin>>n>>m;
std::cin>>a>>b;
int l=0,r=n,res=0;
while(l<=r)
{
int mid=l+r>>1;
if(check(mid)){
l=mid+1;
res=mid;
}else r=mid-1;
}
std::cout<<res<<'\n';
}
signed main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t=1;
std::cin>>t;
while(t--)
{
solve();
}
return 0;
}C. Assembly via Remainders
Problem - C - Codeforces
模拟一下样例即可推结论,本质是模拟。
#include<bits/stdc++.h>
using ll=long long;
const int N=510;
int a[N],b[N];
ll n,m;
void solve()
{
std::cin>>n;
for(int i=2;i<=n;i++)
{
std::cin>>a[i];
}
//a[i]=x[i]%x[i-1]
b[1]=a[2]+1;
for(int i=2;i<=n;i++)
{
if(a[i]<b[i-1]){
b[i]=a[i]+b[i-1];
while(b[i]<=a[i+1])
{
b[i]+=b[i-1];
}
}
}
for(int i=1;i<=n;i++)
{
std::cout<<b[i]<<" ";
}
std::cout<<'\n';
}
signed main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t=1;
std::cin>>t;
while(t--)
{
solve();
}
return 0;
}D. Permutation Game
Problem - D - Codeforces
这个题想法就是,走的走法一定是一直往下走,要么停在一个点,不可能出现走停走的情况。然后我们直接把停在每一个点的情况全都考虑一下就好,比较两个人得分的最大值。
#include<bits/stdc++.h>
using ll=long long;
const int N=2e5+10;
ll a[N],p[N];
ll n,k,pb,ps;
bool st[N];
void solve()
{
memset(st,0,sizeof st);
std::cin>>n>>k>>pb>>ps;
for(int i=1;i<=n;i++)
{
std::cin>>p[i];
}
for(int i=1;i<=n;i++)
{
std::cin>>a[i];
}
ll l=0,r=0;
ll now=pb;
ll nsum=0;
for(ll i=1;i<=std::min(n,k);i++)
{
if(st[now]) break;
st[now]= true;
l=std::max(l,nsum+a[now]*(k-i+1));
nsum+=a[now];
now=p[now];
}
nsum=0,now=ps;
memset(st,0,sizeof st);
for(ll i=1;i<=std::min(n,k);i++)
{
if(st[now]) break;
st[now]= true;
r=std::max(r,nsum+a[now]*(k-i+1));
nsum+=a[now];
now=p[now];
}
//std::cout<<l<<" "<<r<<'\n';
if(l>r) std::cout<<"Bodya"<<'\n';
else if(l<r) std::cout<<"Sasha"<<'\n';
else std::cout<<"Draw"<<'\n';
}
signed main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t=1;
std::cin>>t;
while(t--)
{
solve();
}
return 0;
}E. Cells Arrangement
Problem - E - Codeforces
这题我看的讲解,结论很简单,但是自己考场上想出来确实不那么容易。
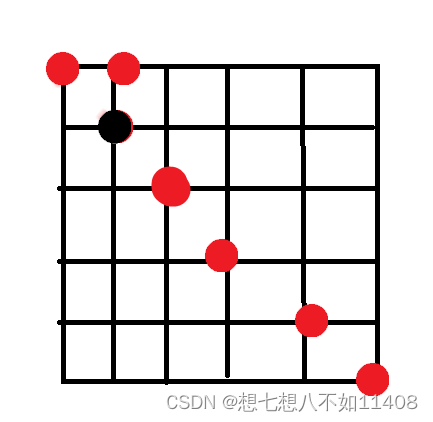
就是一个n*n的棋盘,最多点数也就是从0~2*(n-1),如果能构造出一种方法把这几种情况全都覆盖那么毫无疑问就是最优解。
然后手捏一下会发现n个点全在对角线上的情况,能构造出0、2、4、6,我们只要能构造出一个1就可以了。然后会发现把第二个点移到第一个点旁边就能构造出1了,然后我们就能得到0~2*(n-1)的所有情况。
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
typedef pair<int, int> PII;
void solve()
{
int n;
cin >> n;
cout << "1 1" << endl;
cout << "1 2" << endl;
for (int i = 3; i <= n; i ++ ) {
cout << i << ' ' << i << endl;
}
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int tt; cin >> tt;
while (tt -- ) solve();
return 0;
}