有一个无序整型数组,求该数组排序后的任意两个相邻元素的最大差值;要求时间复杂度和空间复杂度尽可能低。
(1)任意一种时间复杂度为O (nlogn)的排序算法(如快速排序)给原数组排序,然后遍历排好序的数组,并对每两个相邻元素求差,最终得到最大差值。 该解法的时间复杂度是O (nlogn),在不改变原数组的情况下,空间复杂度是O (n)。
(2)计数排序的思想,先找出原数组中最大值和最小值的差。但如果原数组只有3个元素:2,3,1000000,这样就要创建1000000个数组,不可行!
优化方法:使用桶排序的思想(不直接进行桶排序),可以做到时间复杂度O(N),空间复杂度O(N)。

class Bucket:
def __init__(self):
self.max=None
self.min=None
def get_max_sub2(ll):
#1.获取最大值和最小值
max_v=max(ll)
min_v=min(ll)
d=max_v-min_v
# print(max_v,min_v)
#如果等于0,则返回0
if d==0:
return 0
#2.初始化桶
bucket_len=len(ll)
buckets=[]
for i in range(bucket_len):
buckets.append(Bucket())
print(buckets[i].max,buckets[i].min)
#3.循环原数列,确定每个桶的最大值和最小值
for i in range(len(ll)):
#确定数组元素桶的下标
index=int((ll[i]-min_v)*(bucket_len-1)/d)
#判断最大值为空或桶的最大值小于原数列
if buckets[index].max is None or buckets[index].max<ll[i]:
buckets[index].max=ll[i]
if buckets[index].min is None or buckets[index].min>ll[i]:
buckets[index].min=ll[i]
print(index,buckets[index].max,buckets[index].min)
#4.循环桶,找最大差值
#默认左边的第一个最大
leftMax=buckets[0].max
# 最大差
dis_max=0
#循环从第2个开始
for i in range(1,len(buckets)):
#如果最小值为空,继续循环
if buckets[i].min is None:
continue
#如果最小值-第1个最大值大于最大差
if buckets[i].min-leftMax>dis_max:
dis_max=buckets[i].min-leftMax
#获取到最大值
leftMax=buckets[i].max
return dis_max
if __name__ == '__main__':
ll=[22,26,25,21,28,20,34]
print(ll)
print('-'*20)
print("最大差值:",get_max_sub2(ll)) 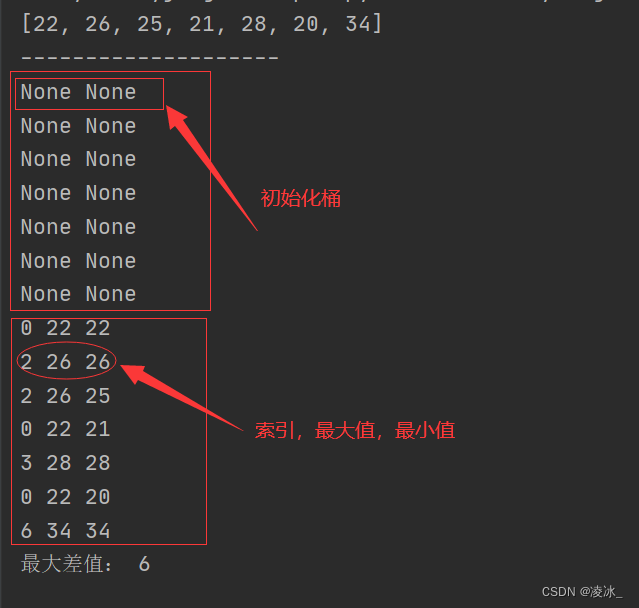






![Linux主机重启后报错:[FAILED] Failed to start Switch Root.](https://img-blog.csdnimg.cn/direct/9ef41a9007ac4c759147649a72270f8d.png)