目录

力扣LCR 130. 衣橱整理（原剑指Offer13机器人的运动范围）

解析代码

---

力扣LCR 130. 衣橱整理（原剑指Offer13机器人的运动范围）

LCR 130. 衣橱整理

难度 中等

家居整理师将待整理衣橱划分为 m x n 的二维矩阵 grid，其中 grid[i][j] 代表一个需要整理的格子。整理师自 grid[0][0] 开始 逐行逐列 地整理每个格子。

整理规则为：在整理过程中，可以选择 向右移动一格 或 向下移动一格，但不能移动到衣柜之外。同时，不需要整理 digit(i) + digit(j) > cnt 的格子，其中 digit(x) 表示数字 x 的各数位之和。

请返回整理师 总共需要整理多少个格子。

示例 1：

输入：m = 4, n = 7, cnt = 5
输出：18

提示：

• 1 <= n, m <= 100
• 0 <= cnt <= 20

class Solution {
public:
    int wardrobeFinishing(int m, int n, int cnt) {

    }
};

---

解析代码

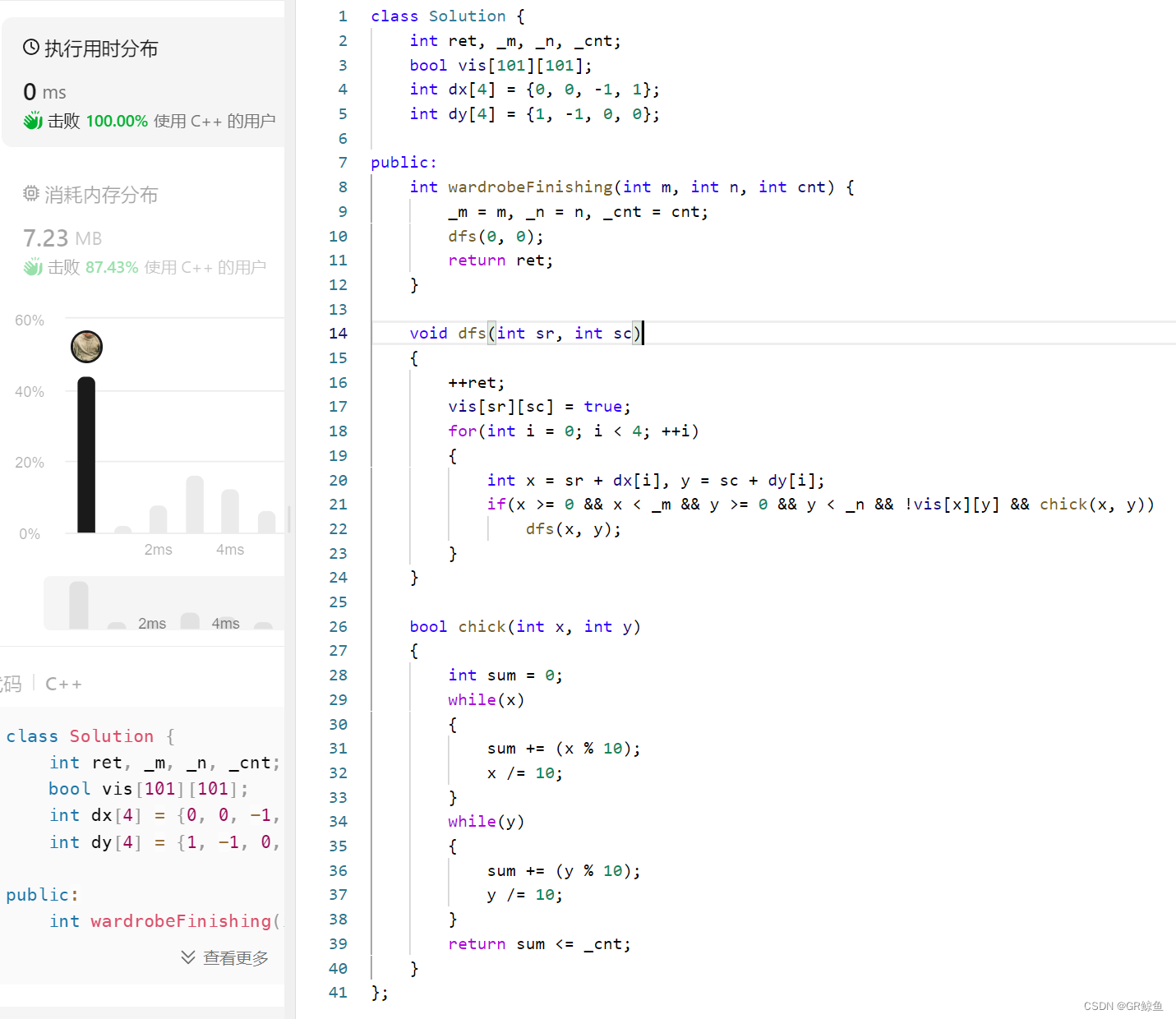
        一道非常典型的搜索类问题。 可以通过深搜或者宽搜，从 [0, 0] 点出发，按照题目的规则一直往 [m - 1, n - 1] 位置走。 同时设置一个全局变量。每次走到一个合法位置，就将全局变量加一。当我们把所有能走到的路都走完之后，全局变量里面存的就是最终答案。下面是深搜的代码：

class Solution {
    int ret, _m, _n, _cnt;
    bool vis[101][101];
    int dx[4] = {0, 0, -1, 1};
    int dy[4] = {1, -1, 0, 0};

public:
    int wardrobeFinishing(int m, int n, int cnt) {
        _m = m, _n = n, _cnt = cnt;
        dfs(0, 0);
        return ret;
    }

    void dfs(int sr, int sc)
    {
        ++ret;
        vis[sr][sc] = true;
        for(int i = 0; i < 4; ++i)
        {
            int x = sr + dx[i], y = sc + dy[i];
            if(x >= 0 && x < _m && y >= 0 && y < _n && !vis[x][y] && chick(x, y))
                dfs(x, y);
        }
    }

    bool chick(int x, int y)
    {
        int sum = 0;
        while(x)
        {
            sum += (x % 10);
            x /= 10;
        }
        while(y)
        {
            sum += (y % 10);
            y /= 10;
        }
        return sum <= _cnt;
    }
};