931. 下降路径最小和

给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：

输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径

示例 2：

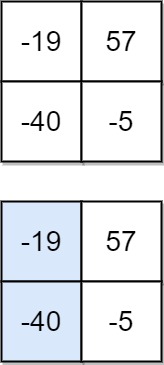
输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：如图所示，为和最小的下降路径

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 100
• -100 <= matrix[i][j] <= 100

class Solution {
    public int minFallingPathSum(int[][] ma) {
        int n = ma.length;
        int[][] dp = new int[n][n];
        for(int i = 0;i < n;i++){
            dp[0][i] = ma[0][i];
        }
        int min = Integer.MAX_VALUE;
        if(n==1){
            for(int i = 0;i < n;i++){
                min = Math.min(min,dp[0][i]);//排除行为1的情况
            }
            return min;
        }
        for(int i = 1;i < n;i++){
            for(int j = 0;j < n;j++){
                if(j==0){//左直边
                    dp[i][j] = Math.min(dp[i-1][j],dp[i-1][j+1]) + ma[i][j];//由上方和右上方推导
                }else if(j==n-1){//右直边
                    dp[i][j] = Math.min(dp[i-1][j],dp[i-1][j-1]) + ma[i][j];//由上方和左上方推导
                }else{
                    dp[i][j] = Math.min(dp[i-1][j],Math.min(dp[i-1][j-1],dp[i-1][j+1])) + ma[i][j];//由上方和左上方和右上方推导
                }
            }
        }
        for(int i = 0;i < n;i++){//找到最小的值
            min = Math.min(min,dp[n-1][i]);
        }
        return min;
    }
}