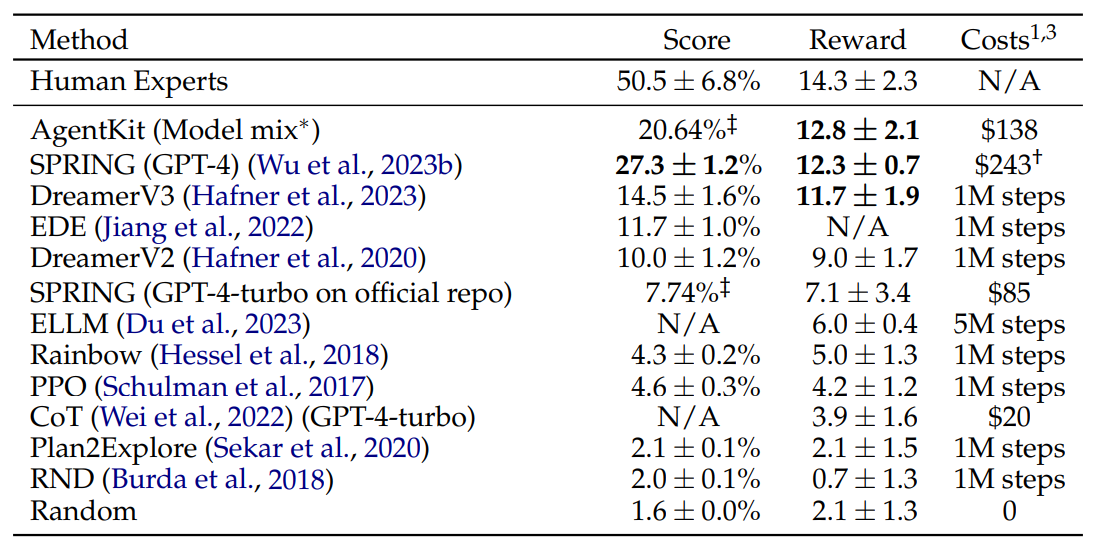
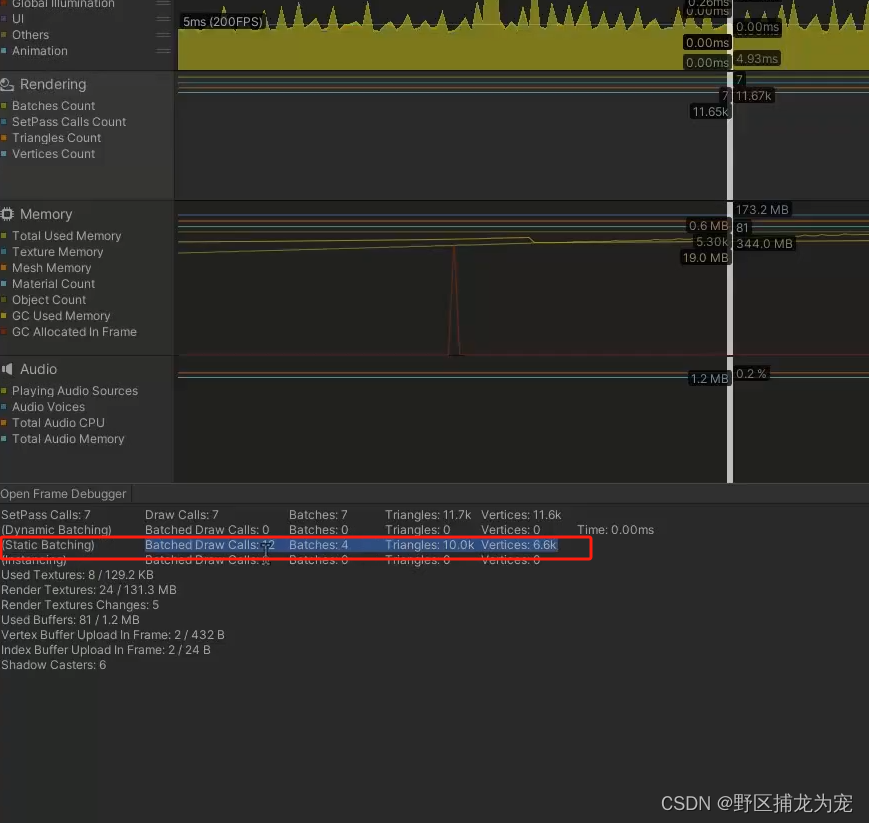
白话特征向量

一个方阵 $A$ 与列向量 $v$ 的乘积会生成一个新的列向量。这个新向量通常与原向量有着不同的方向，矩阵在这里代表一个线性变换。然而，某些向量会保持其原始方向。我们称这种向量为矩阵 $A$ 的特征向量（eigenvector）。

在本文中，我们将探讨特征向量、特征值和矩阵的特征方程。并且以 2 维方阵为例，教大家如何计算矩阵的特征向量和特征值。

举个例子

考虑矩阵 $T$:
$$T=\left(\begin{array}{cc}1& 3\\ 2& 2\end{array}\right)$$
如果将矩阵 $T$ 乘以向量 $(2,0)$ 会得到一个新的向量 $(2,4)$:
$$\left(\begin{array}{cc}1& 3\\ 2& 2\end{array}\right)\left(\begin{array}{c}2\\ 0\end{array}\right)=\left(\begin{array}{c}2\\ 4\end{array}\right)$$
如下图所示。左图中原始向量 $(2,0)$ 用青色表示。它还显示了其他几个不同颜色的向量。右图展示了由上述矩阵 $T$​ 变换后的同一组向量：

一般来讲，右边每个变换后的向量与左边的原始向量相比，其大小和方向都有所不同。

有两个特殊的向量在经过 $T$ 矩阵变换后方向不变，这两个向量是 $(1,1)$ 和 $(-3,2)$​：

这些向量被称为 $T$ 的特征向量。青色向量 $(1,1)$ 被变换为向量 $(4,4)$。变换后的向量与原始向量指向相同的方向，但长度是原来的 $4$ 倍。我们说向量 $(1,1)$ 是 $T$ 的一个特征向量，其特征值为 $4$。

橙色向量 $(-3,2)$ 被变换为向量 $(3,-2)$。它指向与原始向量方向完全相反的方向，换种说法是说它具有相同的方向但长度为负。向量 $(3,-2)$ 等于 $(-3,2)$ 乘以 $-1$，因此我们说这个向量也是 $T$ 的一个特征向量，其特征值为 $-1$。

特征向量的定义

我们用下列方程定义特征向量：
$$Av=\lambda v$$
其中 $A$ 是一个 $n$ 阶方阵（上述示例中是一个 $2$ 阶方阵），$v$ 是一个 $n$ 阶向量，而 $\lambda$ 是一个标量常数。

如果 $v$ 是 $A$ 的一个特征向量，则 $\lambda$ 是对应 $A$ 的特征向量 $v$ 的一个特征值。

通常，特征值的个数等于矩阵的阶数（因此在前面的示例中，有两个特征值，因为它是一个 $2$ 阶矩阵）。每个特征值都与一个特征向量相关联，但请记住，如果 $v$ 是一个特征向量，那么 $v$ 的任何标量倍数也是一个特征向量。重要的只是向量的方向。

此外，有时也可能出现合并情况。例如，一个 $2$ 阶矩阵可能只有一个特征值，对应于两个不共线的不同特征向量。

特征方程

根据上面定义的特征向量的方程 $Av=\lambda v$，我们可以利用单位矩阵来寻找特征值。

单位矩阵是一个方阵，其中主对角线上的每个元素都是 $1$，所有其他元素都是 $0$。如果我们用同阶的单位矩阵乘以任何向量 $v$，它会使向量保持不变：
$$Iv=v$$
因此，我们可以将原方程右侧的 $v$ 替换为 $Ix$，方程仍然成立：
$$Av=\lambda Iv$$
然后将两项都移到方程的左侧并提取公因子 $v$ ，整理后得到下面的方程。
$$(A-\lambda I)v=0$$
注意，上面方程中，$0$ 代表零向量，而不是标量值 $0$。例如，如果 $v$ 是 $2$ 阶向量，则 $0$ 表示 $(0,0)$。

这表明矩阵 $(A-\lambda I)$ 总能将向量 $v$ 变换为 $0$，这意味着其行列式必须为 $0$。因此：
$$|A-\lambda I|=0$$
这便是矩阵 $A$ 的特征方程。我们在这里不进行证明，但这个方程的解就是 $A$ 的特征值，从这些特征值我们可以找到对应的特征向量。

求 $2\times 2$ 矩阵的特征值

让我们用上面介绍的特征方程来求矩阵 $A=\left(\begin{array}{cc}1& 3\\ 2& 2\end{array}\right)$ 的特征向量。其特征方程如下：
$$\begin{array}{rl}|A-\lambda I|& =|\left(\begin{array}{cc}1& 3\\ 2& 2\end{array}\right)-\lambda \left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)|\\ & =|\left(\begin{array}{cc}1& 3\\ 2& 2\end{array}\right)-\left(\begin{array}{cc}\lambda & 0\\ 1& \lambda \end{array}\right)|\\ & =\left|\left(\begin{array}{cc}1-\lambda & 3\\ 2& 2-\lambda \end{array}\right)\right|\end{array}$$
根据 $2$ 阶矩阵的行列式计算公式 $\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|=ad-bc$，可得
$$\begin{array}{rl}|A-\lambda I|=& (1-\lambda )(2-\lambda )-2\cdot 3\\ =& {\lambda }^2-3\lambda -4\end{array}$$
解二次方程 ${\lambda }^2-3\lambda -4=0$ 得，
$$\lambda =-1\lambda =4$$
这就是矩阵 $A$ 都特征值。

利用特征值求特征向量

我们利用 $(A-\lambda I)v=0$ 求特征向量。

上面我们已经推导出 $A-\lambda I=\left(\begin{array}{cc}1-\lambda & 3\\ 2& 2-\lambda \end{array}\right)$ 。代入上面公式可得：
$$(A-\lambda I)v=\left(\begin{array}{cc}1-\lambda & 3\\ 2& 2-\lambda \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=0$$
将上一步求得的特征值 $\lambda =-1,\lambda =4$ 分别代入可得:

• 当 $\lambda =-1$ 时，$\left(\begin{array}{cc}2& 3\\ 2& 2\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=0$，得到如下二元一次方程组
  $$\{\begin{array}{l}2x+3y=0\\ 2x+3y=0\end{array}$$
  这个两个方程是线性相关的（共线的），因此有无数组解，我们只能得到一个关系 $x=-\frac{2}{3}y$​。

  这是一条过原点，斜率为 $-\frac{2}{3}$ 的直线方程。我们的特征向量可以是该线上的任何向量。

  在一开始，我们通过图形的方式展示了向量 $(-3,2)$ 是一个特征向量，这个向量在此直线上。但我们也看到，任何具有相同斜率的向量也是特征向量。因此，例如，$(-6,4)$​ 也是一个特征向量（并且它也满足相同的关系）。存在无数具有不同长度但相同斜率的向量。我们可以选择任何向量，但通常选择具有整数分量的最小向量（如果存在这样的向量）。

• 当 $\lambda =4$ 时，$\left(\begin{array}{cc}-3& 3\\ 2& -2\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=0$​，得到如下二元一次方程组
  $$\{\begin{array}{l}-3x+3y=0\\ 2x-2y=0\end{array}$$
  这个两个方程也是线性相关的（共线的），因此有无数组解，我们得到关系 $x=y$​。

  这同样是一条通原点，斜率为 $1$ 的直线。因此，$(1,1)$ 是一个特征向量，$(2,2)$ 等也是特征向量。