前言
先讲讲我对于这个问题的理解吧
当谈到解决子数组问题时,动态规划(DP)是一个强大的工具,它在处理各种算法挑战时发挥着重要作用。动态规划是一种思想,它通过将问题分解成更小的子问题并以一种递归的方式解决它们,然后利用这些解决方案来构建原始问题的解。在动态规划中,我们经常会遇到两种状态:一种是单独成一段,另一种是以 i 结尾的子数组。
通过枚举和动态规划,我们可以有效地解决子数组问题。枚举法需要考虑所有可能的子数组组合,然后比较它们以找到最优解。这种方法通常需要较多的时间和空间,因为它需要枚举所有可能性。而动态规划则更加智能化,它通过保存历史记录来避免不必要的重复计算。这样,下次遍历时,我们可以利用之前的计算结果,从而大大提高了效率。
动态规划的一个常见技巧是前缀和,它可以帮助我们快速求出数组中任意子数组的和。前缀和的核心思想是将原始数组中每个位置的值累加起来,形成一个新的数组,然后利用这个新数组来快速计算子数组的和。这种方法在处理求子数组和的问题时非常实用,因为它将复杂度降低到了单一状态的动态规划。
另外,预处理也是动态规划中常用的技巧之一。通过将经常使用的数据存储起来,我们可以在需要时快速获取,从而减少计算时间。预处理的思想是在问题出现之前就对数据进行处理,以便在需要时能够迅速获取所需的信息。
综上所述,动态规划是一种强大的解决子数组问题的方法,通过合理利用枚举、动态规划、前缀和和预处理等技巧,我们可以高效地解决各种复杂的算法挑战,为问题提供简单明了的解决方案。
这是我记得笔记

我准备了五道例题都是这些解决方案
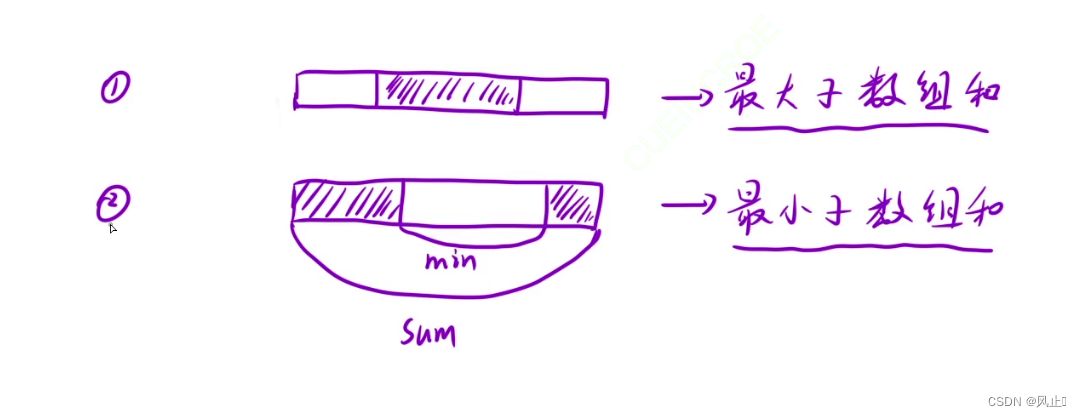
1.求最大子数组的和
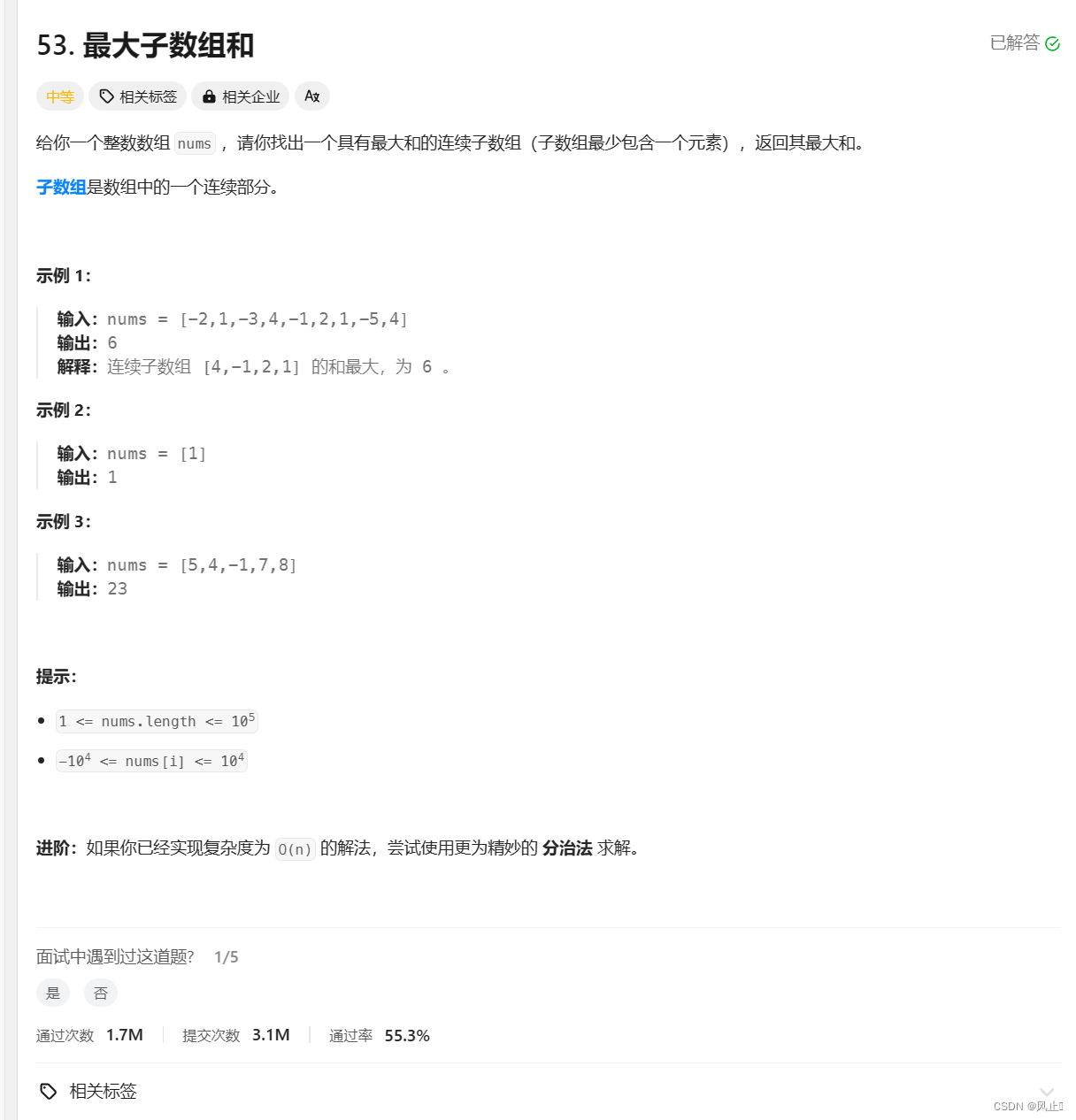
. - 力扣(LeetCode)
思路分析:这一题主要是使用动态规划,也可以使用前缀和,动态规划也是求子数组的普遍思路,有两种状态,1自己组成子数组 和 前面的组成子数组,所以状态转移方程也就是Max(nums[i],dp[i - 1] + nums[i])
代码实现
public int maxSubArray(int[] nums) {
int n = nums.length;
int[] dp = new int[n + 1];//以i位置为结尾的最大子数组和 (多状态 前面i - 1的子数组要 和 不要)
// 初始化 (因为存在负数)
dp[0] = -0x3f3f3f3f;
//前面子数组都是以i - 1位置为结尾 或者 i位置自己构成一个数组
for (int i = 1; i <= nums.length; i++) {
dp[i] = Math.max(nums[i - 1], dp[i - 1] + nums[i - 1]);
}
int max = -0x3f3f3f3f;
for (int i = 0; i < dp.length; i++) {
max = Math.max(dp[i], max);
}
return max;
}2.求最大环形子数组

. - 力扣(LeetCode)
思路分析:
中间的是连续的所以求内部最小子数组和就好了, 或者中间成最大子数组和 //f[]表示以i位置为结尾的所有子数组中的最大值 //g[]表示以i位置为结尾的所有子数组中的最小值 //g[]就是为了处理边界。他通过计算中间部分的最小值来结算环的最大值
public int maxSubarraySumCircular(int[] nums) {
int sum = 0;//用来处理最小值
int n = nums.length;
//1.状态表示
int[] f = new int[n + 1],g = new int[n + 1];
//2.状态转移方程 自己组成子数组 和 自己加上以 i-1位置结尾 的最大子数组
//3.初始化 = 0 即可
for (int i = 1; i <= n; i++) {
f[i] = Math.max(f[i - 1] + nums[i - 1], nums[i - 1]);
g[i] = Math.min(g[i - 1] + nums[i - 1], nums[i - 1]);
sum += nums[i - 1];
}
int maxF = -0x3f3f3f3f;//统计结果
int minG = 0x3f3f3f3f;//统计结果
//可以和上面统一合并,一个循环就够了
for (int i = 1; i <= n; i++) {
maxF = Math.max(maxF,f[i]);
minG = Math.min(minG,g[i]);
}
//为了防止全是负数返回0,所以sum - minG要和0做判断
//因为 -8 - (-8) = 0;全是负数sum = -8 minG = -8 所以要返回maxF
return Math.max(maxF,sum - minG == 0 ? maxF : sum - minG);
}3.和为k的子数组个数
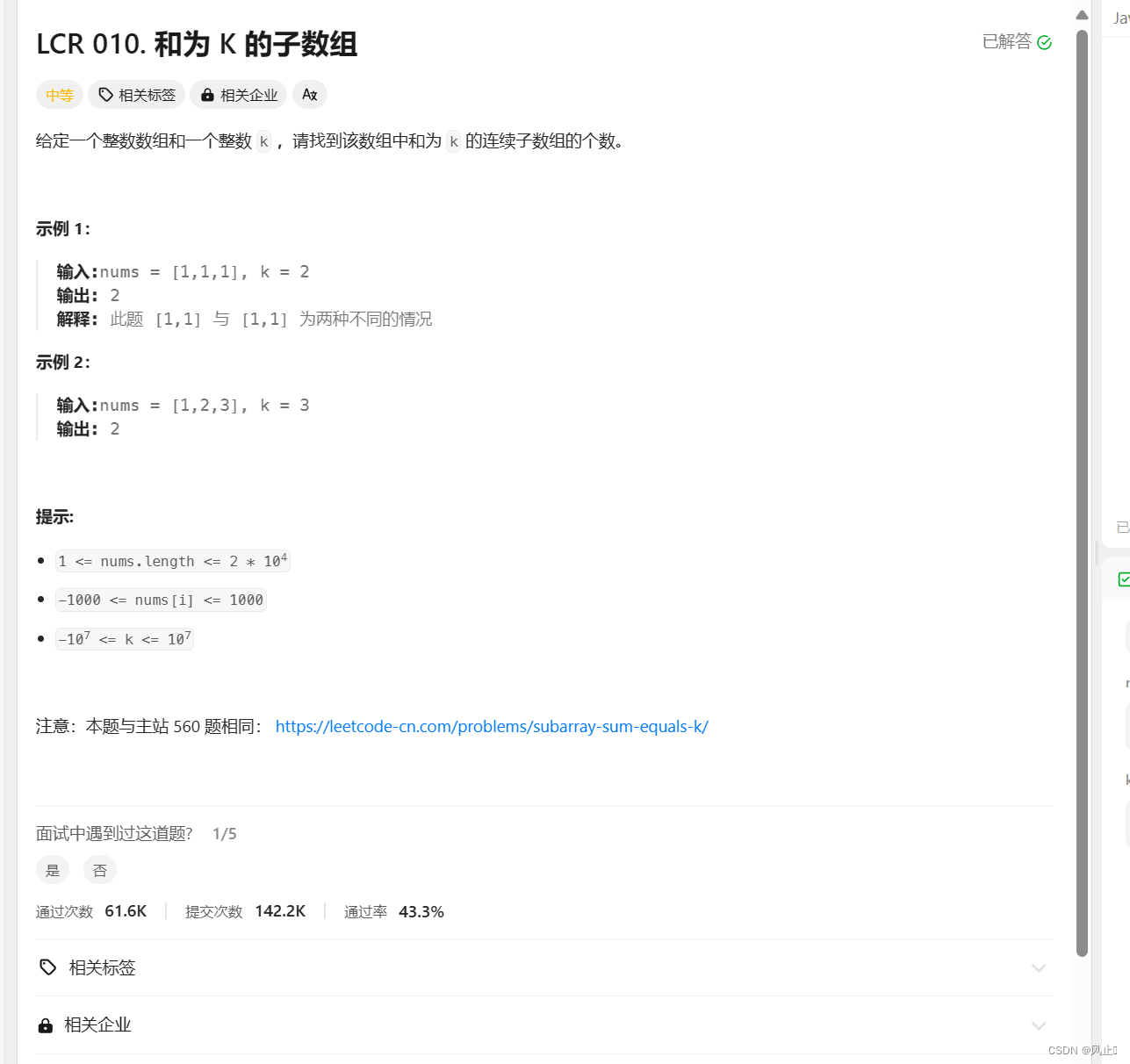
. - 力扣(LeetCode)
思路分析:
//解法 动态规划 + hash表 k == pre[i](i位置的前缀和) - pre[j - 1] //此时 [j,i]的子数组为k
public int subarraySum(int[] nums, int k) {
int count = 0;//统计出现了多少次
int n = nums.length;
HashMap < Integer, Integer > hash = new HashMap<>();//当词典使用,存储所有前缀和
hash.put(0,1);//记录0出现了1次,防止前缀和单独构成答案
//1.状态表示 以i位置为结尾的区间和
int[] pre = new int[n + 1];
//2.状态转移方程 pre[i] = pre[i - 1] + nums[i]
//3.初始化 防止j - 1 越界 pre[0] = 0
for (int i = 1; i <= n; i++) {
pre[i] = pre[i - 1] + nums[i - 1];//下标映射,因为我的pre[0]是虚拟节点
if (hash.containsKey(pre[i] - k)){
count += hash.get(pre[i] - k);
}
hash.put(pre[i],hash.getOrDefault(pre[i],0) + 1);//键为前缀和的值 ,值为出现的次数
}
return count;
}滚动数组优化形成前缀和
//因为上述我们只使用了,pre[i - 1] 和 pre[i] 这两种状态,所以可以使用滚动数组进行优化,设置两个变量即可
//也就是我们熟知的前缀和
public int subarraySum1(int[] nums, int k) {
int count = 0;//统计出现了多少次
int n = nums.length;
HashMap < Integer, Integer > hash = new HashMap<>();//当词典使用,存储所有前缀和
int pre = 0;
hash.put(0,1);//记录0出现了1次,防止前缀和单独构成答案
for (int i = 0; i < n; i++) {
pre += nums[i];
if (hash.containsKey(pre - k)){
count += hash.get(pre - k);
}
hash.put(pre,hash.getOrDefault(pre,0) + 1);//键为前缀和的值 ,值为出现的次数
}
return count;
}4.乘积为k的最大子数组
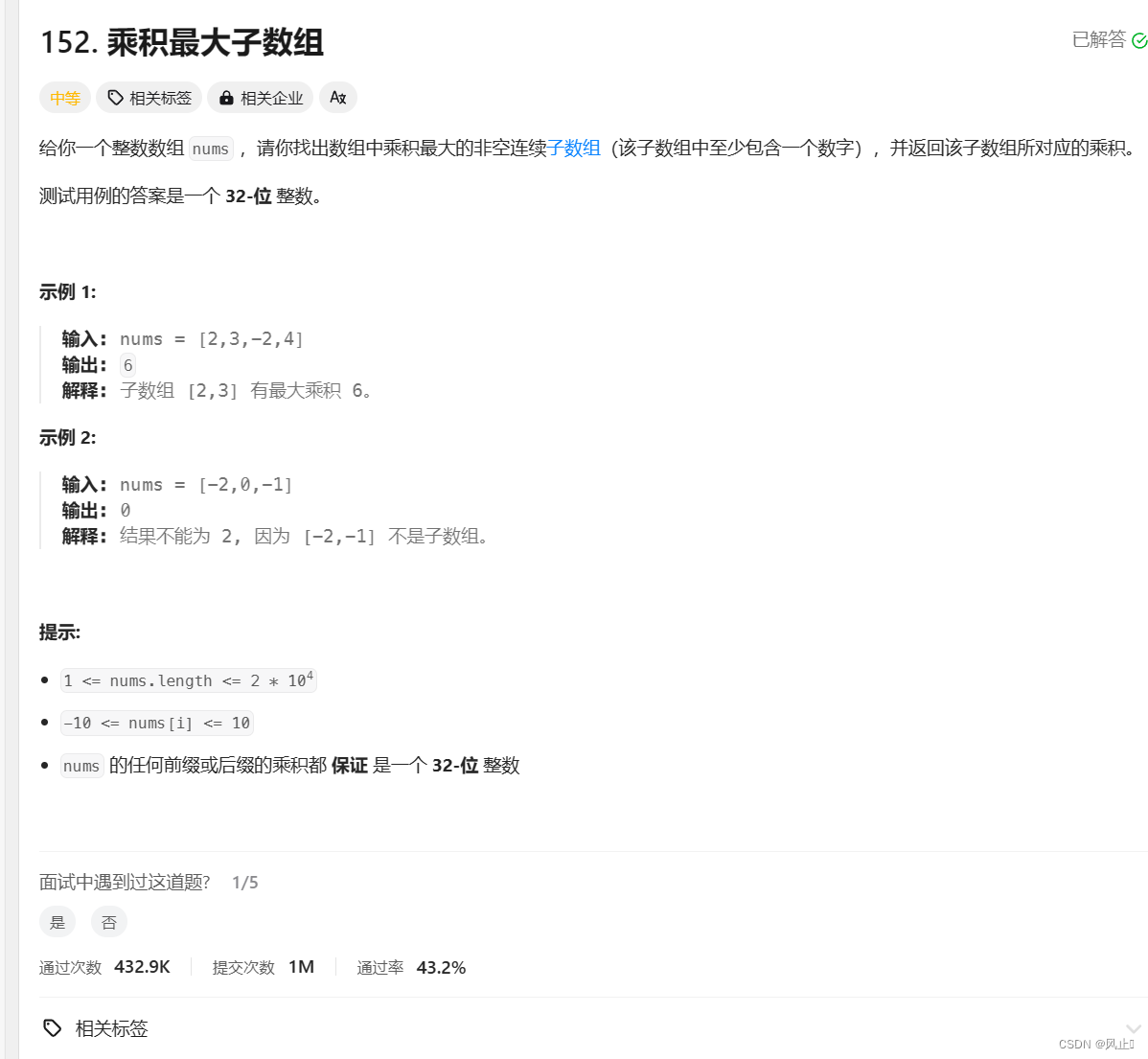
. - 力扣(LeetCode)
思路分析:注释都有明确标注状态表示和转移方程
public int maxProduct(int[] nums) {
int n = nums.length;
//1.定义状态表示
int[] f = new int[n + 1];//以i位置为结尾 所有子数组中 乘积的最大值 遇到正数我要你
int[] g = new int[n + 1];//以i位置为结尾 所有子数组中 乘积的最小值 遇到负数我要你
//2.状态转移方程 遇到正数我要最大值(f[i - 1]) 遇到负数我要最小值(g[i - 1])
//3.初始化 防止i - 1越界但不可保存0,因为初始化的初衷就是保证后续的位置不受影响
f[0] = g[0] = 1;//注意多次赋值是从右往左进行的
int ret = -0x3f3f3f3f;
for (int i = 1; i <= n; i++) {
if (nums[i - 1] > 0){
f[i] = Math.max(f[i - 1] * nums[i - 1],nums[i - 1]);
g[i] = Math.min(g[i - 1] * nums[i - 1],nums[i - 1]);
}else {
f[i] = Math.max(g[i - 1] * nums[i - 1],nums[i - 1]);
g[i] = Math.min(f[i - 1] * nums[i - 1],nums[i - 1]);
}
ret = Math.max(ret,f[i]);
}
return ret;
}5.乘积为正数的最长子数组长度

. - 力扣(LeetCode)
public int getMaxLen(int[] nums) {
int n = nums.length;
int ret = 0;//统计
//1.状态表示
int[] f = new int[n + 1];//以i位置为结尾中的 所有子数组中的 乘积为正数的最大长度
int[] g = new int[n + 1];//以i位置为结尾中的 所有子数组中的 乘积为负数的最大长度
//2.状态转移方程 f[i]如果i位置为正数为 f[i - 1] + 1 负数 g[i - 1] + 1
// g[i]同理正数g[i - 1] + 1 负数 f[i - 1] + 1
//3.初始化 默认长度为0不影响后续结果
for (int i = 1; i <= n; i++) {
if (nums[i - 1] > 0){
f[i] = f[i - 1] + 1;
//当最后一个元素为正数的时候,并且g[i - 1] = 0表示前面没有负数,所以不可能组成负数
g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;
}else if (nums[i - 1] < 0){
//当最后一个元素为负数的时候,并且g[i - 1] = 0表示前面没有负数,所以不可能组成正数
f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;
g[i] = f[i - 1] + 1;
}else {//处理为0的情况
f[i] = 0;
g[i] = 0;
}
ret = Math.max(ret,f[i]);
}
return ret;
}总结
当解决子数组问题时,动态规划是一个强大而智能的工具。通过将问题分解成更小的子问题并以递归的方式解决它们,动态规划可以高效地找到原始问题的解。在动态规划中,我们常常会遇到两种状态:一种是单独成一段,另一种是以 i 结尾的子数组。
枚举和动态规划是解决子数组问题的两种主要方法。枚举法需要考虑所有可能的子数组组合,然后比较它们以找到最优解。而动态规划则通过保存历史记录来避免不必要的重复计算,从而提高效率。
在动态规划中,常用的技巧包括前缀和和预处理。前缀和可以帮助我们快速求出数组中任意子数组的和,而预处理则可以在问题出现之前就对数据进行处理,以提高计算效率。
综上所述,动态规划是解决子数组问题的一种强大工具,通过合理利用枚举、动态规划、前缀和和预处理等技巧,我们可以高效地解决各种复杂的算法挑战,为问题提供简单明了的解决方案。