一、前言

变分自编码器（Variational Auto-Encoder，VAE）是以自编码器结构为基础的深度生成模型。

自编码器（ Auto-Encoder，AE）在降维和特征提取等领域应用广泛, 基本结构是通过编码 (Encoder) 过程将样本映射到低维空间的隐变量, 然后通过解码 (Decoder) 过程将隐变量还原为重构样本。

其中，对于编码层：

图中的输入数据$x$与对应的连接权重$W$相乘，再加上偏置$b$，经过激活函数$f(\cdot )$变换后，得到$y$。具体公式如下：

$$y=f(Wx+b)$$

对于解码层：

中间层和重构层之间的连接权重及偏置分为记作$\tilde{W}$和$\tilde{b}$，激活函数为$\tilde{f}(\cdot )$，重构结果记作$\tilde{x}$。

$$\tilde{x}=\tilde{f}\left(\tilde{W}y+\tilde{b}\right)$$

因此，自编码器总的过程可以表示为：

$$\tilde{x}=\tilde{f}(\tilde{W}f(Wx+b)+\tilde{b})$$

损失函数（Loss函数）$L$可以使用最小二乘法差函数或者交叉熵代价函数。

$$\begin{gathered} L=\sum _{n=1}^N\Vert x_n-\widetilde{x_n}{\Vert }^2 \\ L=-\sum _{n=1}^N(x_{i}log{\tilde{x}}_i+(1-x_i)log(1-{\tilde{x}}_i)) \end{gathered}$$

二、变分自编码器

1、VAE的目标

VAE的目标是先假设一个隐变量$Z$的分布，构建一个从$Z$到目标数据$X$的模型，即构建$X=g(Z)$，使得学出来的目标数据与真实数据的概率分布相近。与GAN基本一致，GAN学的也是概率分布。

图1 VAE示意图

2、理论推导

首先我们有一批数据样本 { X 1 , … , X n } \{X_1,…,X_n\} {X1​,…,Xn​}，其整体用$X$来描述，我们本想根据 { X 1 , … , X n } \{X_1,…,X_n\} {X1​,…,Xn​}得到$X$的分布$P(x)$，如果能得到的话，那我直接根据$P(x)$来采样，就可以得到所有可能的$X$了（包括 { X 1 , … , X n } \{X_1,…,X_n\} {X1​,…,Xn​}+ { X 1 , … , X n } \{X_1,…,X_n\} {X1​,…,Xn​}以外的），这是一个终极理想的生成模型了。当然，这个理想很难实现，于是我们将分布改一改，就变成了

原始的样本数据$x$的概率分布：

$$P(x)={\int }_{z}P(z)P(x|z)dz$$

假设$z$服从标准高斯分布，则$P(x)$就是在积分域上所有高斯分布的累加。

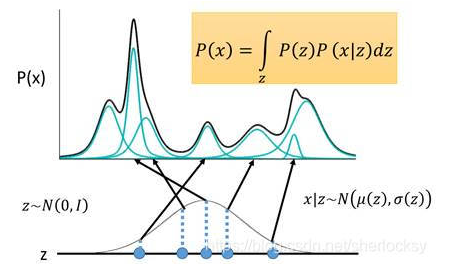
图2 $P(x)$分布累加

由于$P(z)$是已知的，$P(x|z)$未知。我们最开始的目标是求解$P(x)$，且我们希望$P(x)$越大越好，这等价于求解关于$x$最大对数似然：

$$L=\sum _{x}logP(x)$$

而$logP(x)$可变换为：

$$\begin{array}{rl}logP(x)& ={\int }_{z}Q(z|x)logP(x)dz\\ & ={\int }_{z}Q(z|x)log\frac{P(z,x)}{P(z|x)}dz\\ & ={\int }_{z}Q(z|x)log(\frac{P(z,x)}{Q(z|x)}\frac{Q(z|x)}{P(z|x)})dz\\ & ={\int }_{z}Q(z|x)log(\frac{P(z,x)}{Q(z|x)})dz+{\int }_{z}Q(z|x)log(\frac{Q(z|x)}{P(z|x)})dz\\ & ={\int }_{z}Q(z|x)log(\frac{P(x|z)P(z)}{Q(z|x)})dz+{\int }_{z}Q(z|x)log(\frac{Q(z|x)}{P(z|x)})dz\\ & ={\int }_{z}Q(z|x)log(\frac{P(x|z)P(z)}{Q(z|x)})dz+KL(Q(z|x)||P(z|x))\end{array}$$

注：
${\int }_{z}Q(z|x)log(\frac{Q(z|x)}{P(z|x)})dz=KL(Q(z|x)||P(z|x)$

因为KL散度是大于等于0的，可以进一步得到：

$$logP(x)⩾{\int }_{z}Q(z|x)log(\frac{P(x|z)P(z)}{Q(z|x)})dz$$

这样我们就找到了一个下界（lower bound），也就是式子的右项，即

$$L_b={\int }_{z}Q(z|x)log(\frac{P(x|z)P(z)}{q(z|x)})dz$$

原式也可表示成：

$$logP\left(x\right)=L_b+KL(Q(z|x)||P(z|x))$$

实际上，因为后验分布$P(z|x)$很难求，所以才用$Q(z|x)$来逼近这个后验分布。在优化的过程中我们发现，首先$Q(z|x)$跟$logP\left(x\right)$是完全没有关系的，$logP\left(x\right)$只跟$P(z|x)$有关，调节$Q(z|x)$是不会影响似然，也就是$logP\left(x\right)$的。所以，当我们固定住$P(z|x)$时，调节$Q(z|x)$，从而最大化下界$L_b$，KL则越小。当$Q(z|x)$与不断逼近后验分布$P(z|x)$时，KL散度趋于为0，$logP\left(x\right)$就和$L_b$等价，所以最大化$logP\left(x\right)$就等价于最大化$L_b$。

因为由前边的推导可以知道

$$\begin{array}{rl}{L}_b& ={\int }_{z}Q(z|x)log(\frac{P(x|z)P(z)}{Q(z|x)})dz\\ & ={\int }_{z}Q(z|x)log(\frac{P(z)}{Q(z|x)})dz+{\int }_{z}Q(z|x)log(P(x|z))dz\\ & =-KL(Q(z|x)||P(z))+{\int }_{z}Q(z|x)log(P(x|z))dz\\ & =-KL(Q(z|x)||P(z))+E_{q(x|z)}[log(P(x|z))]\end{array}$$

显然，最大化$L_b$等价于最小化$-KL(Q(z|x)||P(z))$和最大化$E_{q(x|z)}[log(P(x|z))]$。

假设$P(z)$服从标准正态分布，且$Q(z|x)$服从高斯分布$N(\mu ,{\sigma }^2)$，于是代入计算可得：

$$\begin{array}{rl}KL(Q(z|x)||P(z))& =KL(N(\mu ,{\sigma }^2)||N(0,I))\\ & =\int \frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{\frac{-(x-\mu {)}^2}{2{\sigma }^2}}\left(log\frac{e^{\frac{-(x-\mu {)}^2}{2{\sigma }^2}}/\sqrt{2\pi {\sigma }^2}}{e^{\frac{-x^2}{2}}/\sqrt{2\pi }}\right)dx\\ & =\frac{1}{2}\frac{1}{\sqrt{2\pi {\sigma }^2}}\int e^{\frac{-(x-\mu {)}^2}{2{\sigma }^2}}(-log{\sigma }^2+x^2-\frac{(x-\mu {)}^2}{{\sigma }^2})dx\\ & =\frac{1}{2}\int \frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{\frac{-(x-\mu {)}^2}{2{\sigma }^2}}(-log{\sigma }^2+x^2-\frac{(x-\mu {)}^2}{{\sigma }^2})dx\end{array}$$

对上式中的积分进一步求解：

（1）$\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{\frac{-(x-\mu {)}^2}{2{\sigma }^2}}$实际就是概率密度$f(x)$，而概率密度的积分为$1$，所以积分第一项等于$-log{\sigma }^2$。

（2）而又因为高斯分布的二阶矩就是$E(x^2)=\int x^{2}f(x)dx={\mu }^2+{\sigma }^2$，正好是对应积分第二项。

（3）根据方差的定义可知${\sigma }^2=\int (x-\mu {)}^{2}dx$，所以积分第三项为$-1$。

最终结果为：

$$\begin{array}{rl}KL(Q(z|x)||P(z))& =KL(N(\mu ,{\sigma }^2)||N(0,1))\\ & =\frac{1}{2}(-log{\sigma }^2+{\mu }^2+{\sigma }^2-1)\end{array}$$

也就是表明在给定$Q(z|x)$（编码器输出）的情况下$P(x|z)$（解码器）输出的值尽可能高。具体来讲：

（1）利用encoder的神经网络计算出均值与方差，从中采样得到$z$，这一过程就对应式子中的$Q(z|x)$。

（2）利用decoder的NN计算$z$的均值方差，让均值（或也考虑方差）越接近$z$，则产生$x$的几率$log(P(x|z))$越大，对应于式子中的最大化$log(P(x|z))$这一部分。

3、补充

其实，在整个VAE模型中，我们并没有去使用$P(Z)$（隐变量空间的分布）是正态分布的假设，我们用的是假设$Q(Z|X)$（后验分布）是正态分布。

具体来说，给定一个真实样本$X_k$，我们假设存在一个专属于$X_k$的分布$Q(Z|X_k)$（学名叫后验分布），并进一步假设这个分布是（独立的、多元的）正态分布。

为什么要强调“专属”呢？

因为我们后面要训练一个生成器$X=g(Z)$，希望能够把从分布$Q(Z|X_k)$采样出来的一个$Z_k$还原为$X_k$。如果假设$P(Z)$是正态分布，然后从$P(Z)$中采样一个$Z$，那么我们怎么知道这个$Z$对应于哪个真实的$X$呢？现在$p(Z|X_k)$专属于$X_k$，我们有理由说从这个分布采样出来的$Z$应该要还原到$X_k$中去。

这时候每一个$X_k$都配上了一个专属的正态分布，才方便后面的生成器做还原。但这样有多少个$X$就有多少个正态分布了。我们知道正态分布有两组参数：均值$\mu$和方差${\sigma }^2$（多元的话，它们都是向量），那我怎么找出专属于$X_k$的正态分布$Q(Z|X_k)$的均值和方差呢？

用神经网络来拟合！

于是我们构建两个神经网络${\mu }_k=f_1(X_k)$，$log{\sigma }_k^2=f_2(X_k)$来算它们了。

我们选择拟合$log{\sigma }_k^2$而不是直接拟合${\sigma }_k^2$，是因为${\sigma }_k^2$总是非负的，需要加激活函数处理，而拟合$log{\sigma }_k^2$不需要加激活函数，因为它可正可负。

到这里，就能知道专属于$X_k$的均值和方差了，也就知道它的正态分布长什么样了，然后从这个专属分布中采样一个$Z_k$出来，然后经过一个生成器得到$X_k=g(Z_k)$，现在我们可以放心地最小化$D({\hat{X}}_k,X_k{)}^2$，因为$Z_k$是从专属$X_k$的分布中采样出来的，这个生成器应该要把开始的$X_k$还原回来。示意图如图1所示。

根据上边图1描述的过程，首先，我们希望重构$X$，也就是最小化$D({\hat{X}}_k,X_k{)}^2$，但是这个重构过程受到噪声的影响，因为$Z_k$是通过重新采样过的，不是直接由encoder算出来的。显然噪声会增加重构的难度，不过好在这个噪声强度（也就是方差）通过一个神经网络算出来的，所以最终模型为了重构得更好，肯定会想尽办法让方差为0。而方差为0的话，也就没有随机性了，所以不管怎么采样其实都只是得到确定的结果（也就是均值），只拟合一个当然比拟合多个要容易，而均值是通过另外一个神经网络算出来的。

这样的话，模型会慢慢退化成普通的AutoEncoder，噪声不再起作用。

其实VAE还让所有的$Q(Z|X)$都向标准正态分布看齐，这样就防止了噪声为零，同时保证了模型具有生成能力。怎么理解“保证了生成能力”呢？如果所有的$Q(Z|X)$都很接近标准正态分布$N(0,I)$，那么根据定义

$$\begin{array}{rl}P(Z)& =\sum _{X}Q(Z|X)P(X)\\ & =\sum _X\mathcal{N}(0,I)P(X)\\ & =\mathcal{N}(0,I)\sum _{X}P(X)\\ & =\mathcal{N}(0,I)\end{array}$$

这样我们就能达到我们的先验假设：$P(Z)$是标准正态分布。此时，原始的示意图1变为了下边的形式。

图3 分布标准化后的VAE示意图

那怎么让所有的$Q(Z|X)$都向$N(0,I)$看齐呢？如果没有外部知识的话，其实最直接的方法应该是在重构误差的基础上中加入额外的$loss$：

$$\begin{array}{rl}{\mathcal{L}}_{\mu }& =\Vert f_1(X_k){\Vert }^2\\ {\mathcal{L}}_{{\sigma }^2}& =\Vert f_2(X_k){\Vert }^2\end{array}$$

因为它们分别代表了均值${\mu }_k$和方差的对数$log{\sigma }_k^2$，达到$N(0,I)$就是希望二者尽量接近于$0$了。不过，这又会面临着这两个损失的比例要怎么选取的问题，选取得不好，生成的图像会比较模糊。所以，原论文直接算了一般（各分量独立的）正态分布与标准正态分布的KL散度$KL(N(\mu ,{\sigma }^2)\Vert \Vert N(0,I))$作为这个额外的$loss$，计算结果为

$$KL(N(\mu ,{\sigma }^2)\Vert N(0,1))=\frac{1}{2}(-\log {\sigma }^2+{\mu }^2+{\sigma }^2-1)$$

与之前的结果一致。

4、重参数技巧

要从$Q(Z|X_k)$中采样一个$Z_k$出来，尽管我们知道了$Q(Z|X_k)$是正态分布，但是均值方差都是靠模型算出来的，我们要靠这个过程反过来优化均值方差的模型，但是“采样”这个操作是不可导的，而采样的结果是可导的。我们利用

$$\begin{array}{rl}& \frac{1}{\sqrt{2\pi {\sigma }^2}}\exp (-\frac{(z-\mu {)}^2}{2{\sigma }^2})dz\\ =& \frac{1}{\sqrt{2\pi }}\exp \left[-\frac{1}{2}{\left(\frac{z-\mu }{\sigma }\right)}^2\right]d\left(\frac{z-\mu }{\sigma }\right)\end{array}$$

这说明$(z-\mu )/\sigma =\epsilon$是服从均值为$0$、方差为$1$的标准正态分布的，要同时把$dz$考虑进去，是因为乘上$dz$才算是概率，去掉$dz$是概率密度而不是概率。这时候我们得到：

从$N(\mu ,{\sigma }^2)$中采样一个$Z$，相当于从$N(0,I)$中采样一个$\epsilon$，然后让$Z=\mu +\epsilon \times \sigma$。

于是，我们将从$N(\mu ,{\sigma }^2)$采样变成了从$N(0,I)$中采样，然后通过参数变换得到从$N(\mu ,{\sigma }^2)$中采样的结果。这样一来，“采样”这个操作就不用参与梯度下降了，改为采样的结果参与，使得整个模型可训练了。

参考：
1、详解VAE（变分自编码器）
2、变分自编码器（一）：原来是这么一回事