图像压缩问题的bilibil讲解

1.问题引入

首先，图像是由像素组合成的，每个像素都有灰度值，灰度值是体现像素的颜色的。灰度值从0~255，灰度值占用的位数就是像素占用的位数。我们要存储一个图像就要存储它的所有像素。现在的问题是我们如何存储，使得存储空间最小？

思路：我们需要将图像分成m段，每段中有L[t]个像素，每个要占用b[t]个比特位，每个段都有一个端头，段头是固定的需要占用11位。因此总共需要如下存储空间。

一段像素个数最多有256个，这是题目要求的已知条件。一个像素要最少要占用多少位哩？设第t个像素的灰度值为n，b[t]（每个像素占用的位数）要考虑到2种情况，第一种，n是2的整数次方，这时b[t]就是logn；第二种情况，a<logn<b(a,b为整数），这时要保证能表示灰度值，要加一再向上取整。综上，我们要满足这两种情况的并集，b[t]=log(n+1)向上取整，注意不能是log(n)+1向上取整，因为如果（n=2的x次方-1）时，这两种值就不一样了。例如，灰度值为1，我们需要一位来存储。再如，n=7,我们需要3位来存储。第t段最大的像素所占位数为max pk,得到如下图所示：

一个例子：

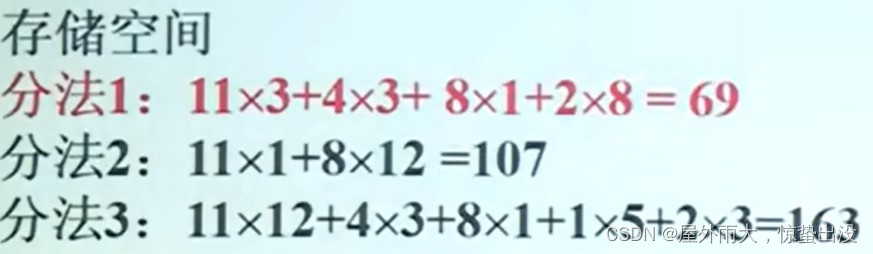
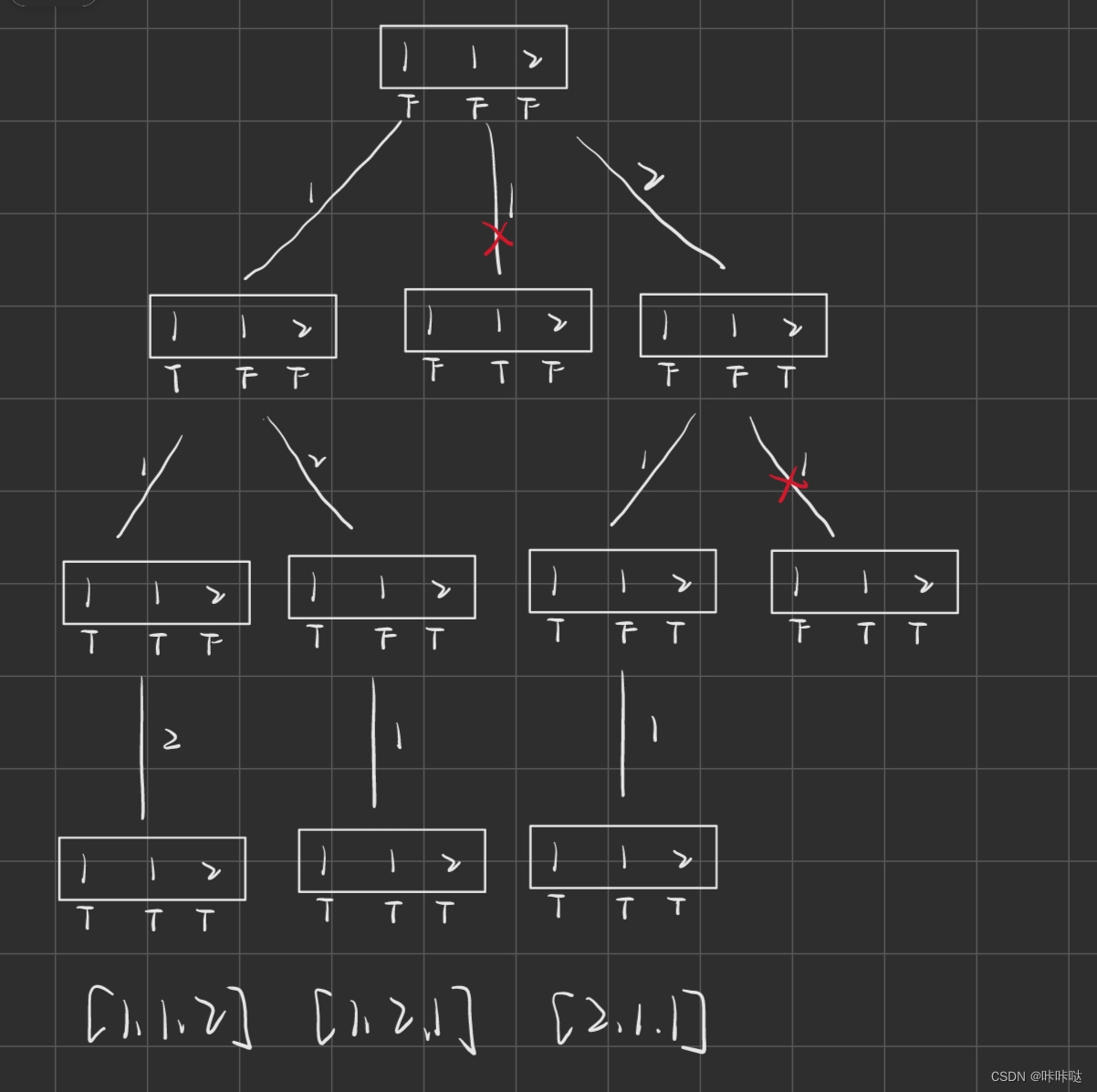
对于这个问题就转变成了如何分段问题。如果要用暴力求解法，我们要遍历多少种分段方法哩？

假设一共有n个像素，那么就有n-1个分割点，每个分割点可以选择分或不分，一共有2的n-1次方种分段方法

显然，比较浪费时间。

2.用动态规划算法可以减少时间复杂度，那么动态归划算法怎么划分子问题呢？

我们只用一个变量i来表示第i个像素的位置，找到第i个位置的最优解，每次增加一个像素，最终变成规模为n的像素问题。

例子：

上面例子种S[1]=4+11=15

S[2]的最优解在这两种划分方法中（1）分2段：S[1]+4+11=30  (2)分1段：S[0]+4*2+11=19

S[3]的最优解在这三种划分方法中（1）S[1]+4*2+11=34  (2)S[2]+4+11=34 (3)S[0]+4*3+11=23

S[4]的最优解在这四种划分方法中（1）S[3]+8+11=42 (2)S[2]+8*2+11 (3)S[1]+8*3+11 (4)S[0]+8*4+11

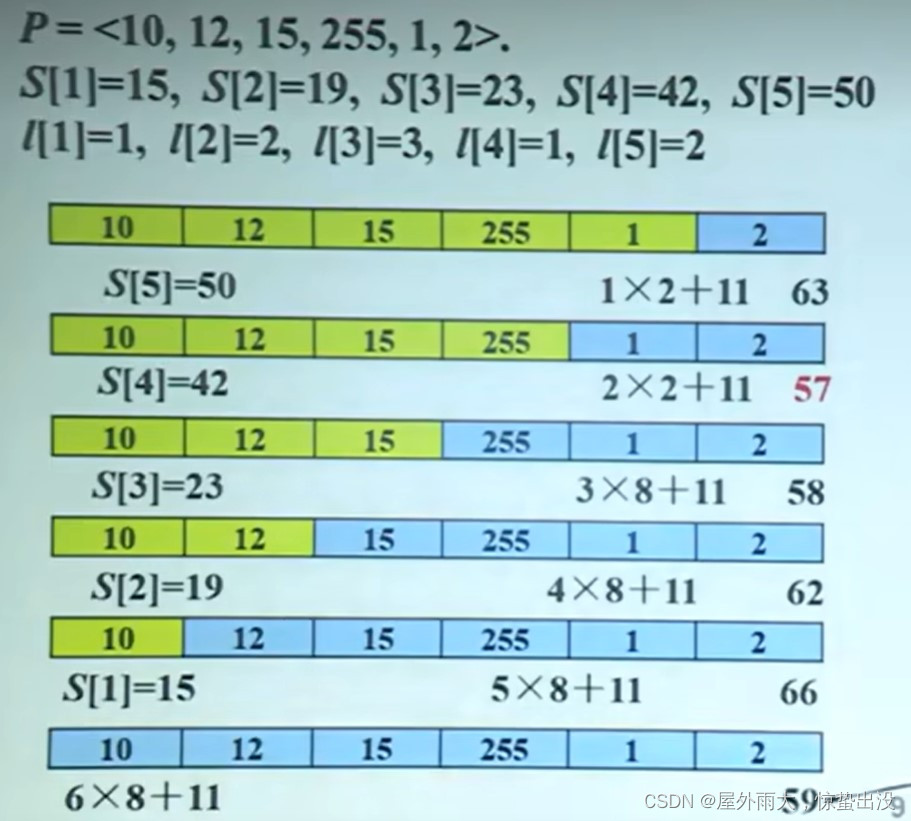
依次类推，S[6]的最优解在如上图所示这六种划分算法中。

（1）S[5]+1*2+11 (2)S[4]+2*2+11 (3) S[3]+3*8+11 (4)S[2]+4*8+11

(5)S[1]+5*8+11 (6) S[0]+6*8+11

红色部分对应代码

s[i] = s[i - 1] + bmax;//整个数组从1到i-1的最优解加i单独一段

  s[i] += header;

黄色部分对应代码

//在s[i]+j*bmax中找最好的存储方法
        for (int j = 2; j <= i && j <= Lmax; j++)
        {
            if (bmax < b[i - j + 1])//下标前移，找最大的像素
            {
                bmax = b[i - j + 1];
            }

            if (s[i] > s[i - j] + j * bmax)
            {
                s[i] = s[i - j] + j * bmax;
                l[i] = j;
            }
        }
        s[i] += header;

其中，L[i]记录S[i]的划分段数。

3.接下来，我们看看递推方程怎么表示

从j-i+1到i个像素中占用位数最大的像素记为b[i-j+1,i]

S[i]表示从第一个像素到第i个像素的最小存储总位数。

4.伪代码实现

s[i]来记录前i个数字的最优处理方式得到的最优解，即最小存储位数
l[i]来记录当前第i个数所在段中有多少个数，
b[i]中存放前i个像素点的最后一段中最大像素位数。

5.代码实现

#include <iostream>   
using namespace std;

const int N = 8;

int length(int i);
void Compress(int n, int p[], int s[], int l[], int b[]);
void Tracebace(int n, int& i, int s[], int l[]);
void Output(int s[], int l[], int b[], int n);

int main()
{
    int p[] = { 0,10,12,15,255,1,2,0 };//图像灰度数组 下标从1开始计数  
    int s[N], l[N], b[N];
/**s[i]来记录前i个数字的最优处理方式得到的最优解，即最小存储位数
l[i]来记录当前第i个数所在段中有多少个数，
b[i]中存放前i个像素点的最后一段中最大像素位数。**/

    cout << "图像的灰度序列为：" << endl;

    for (int i = 1; i < N; i++) //输出原灰度序列 
    {
        cout << p[i] << " ";
    }
    cout << endl;

    Compress(N - 1, p, s, l, b);
    Output(s, l, b, N - 1);
    return 0;
}

void Compress(int n, int p[], int s[], int l[], int b[])
{
    int Lmax = 256, header = 11;
    s[0] = 0;
    for (int i = 1; i <= n; i++)
    {
        b[i] = length(p[i]); //计算像素点p需要的存储位数  
        int bmax = b[i];
        s[i] = s[i - 1] + bmax;//整个数组从1到i-1的最优解加i单独一段
        l[i] = 1;
//在s[i]+j*bmax中找最好的存储方法
        for (int j = 2; j <= i && j <= Lmax; j++)
        {
            if (bmax < b[i - j + 1])//下标前移，找最大的像素
            {
                bmax = b[i - j + 1];
            }

            if (s[i] > s[i - j] + j * bmax)
            {
                s[i] = s[i - j] + j * bmax;
                l[i] = j;
            }
        }
        s[i] += header;
    }
}
/***求数组中的元素用多少位二进制表示***/
int length(int i) //i表示p数组中元素的值 
{
    int k = 1;
    i = i / 2;
    while (i > 0)
    {
        k++;
        i = i / 2;
    }
    return k;
}
/**s[i]来记录前i个数字的最优处理方式得到的最优解，即最小存储位数
l[i]来记录当前第i个数所在段中有多少个数，
b[i]中存放前i个像素点的最后一段中最大像素位数。**/
/*递归找寻分段的位置*/
void Traceback(int n, int& i, int s[], int l[])
{
    if (n == 0)
        return;
    Traceback(n - l[n], i, s, l);
    s[i++] = n - l[n];//重新为s[]数组赋值，用来存储分段位置  
}

void Output(int s[], int l[], int b[], int n)
{
    //在输出s[n]存储位数后，s[]数组则被重新赋值，用来存储分段的位置  
    cout << "图像压缩后的最小空间为：" << s[n] << endl;
    int m = 0;
    Traceback(n, m, s, l);
    s[m] = n;
    cout << "将原灰度序列分成" << m << "段序列段" << endl;
    for (int j = 1; j <= m; j++)
    {
        l[j] = l[s[j]];//在下标为s[j]的地方划分
        b[j] = b[s[j]];
    }
    for (int j = 1; j <= m; j++)
    {
        cout << "段长度：" << l[j] << ",所需存储位数:" << b[j] << endl;
    }
}