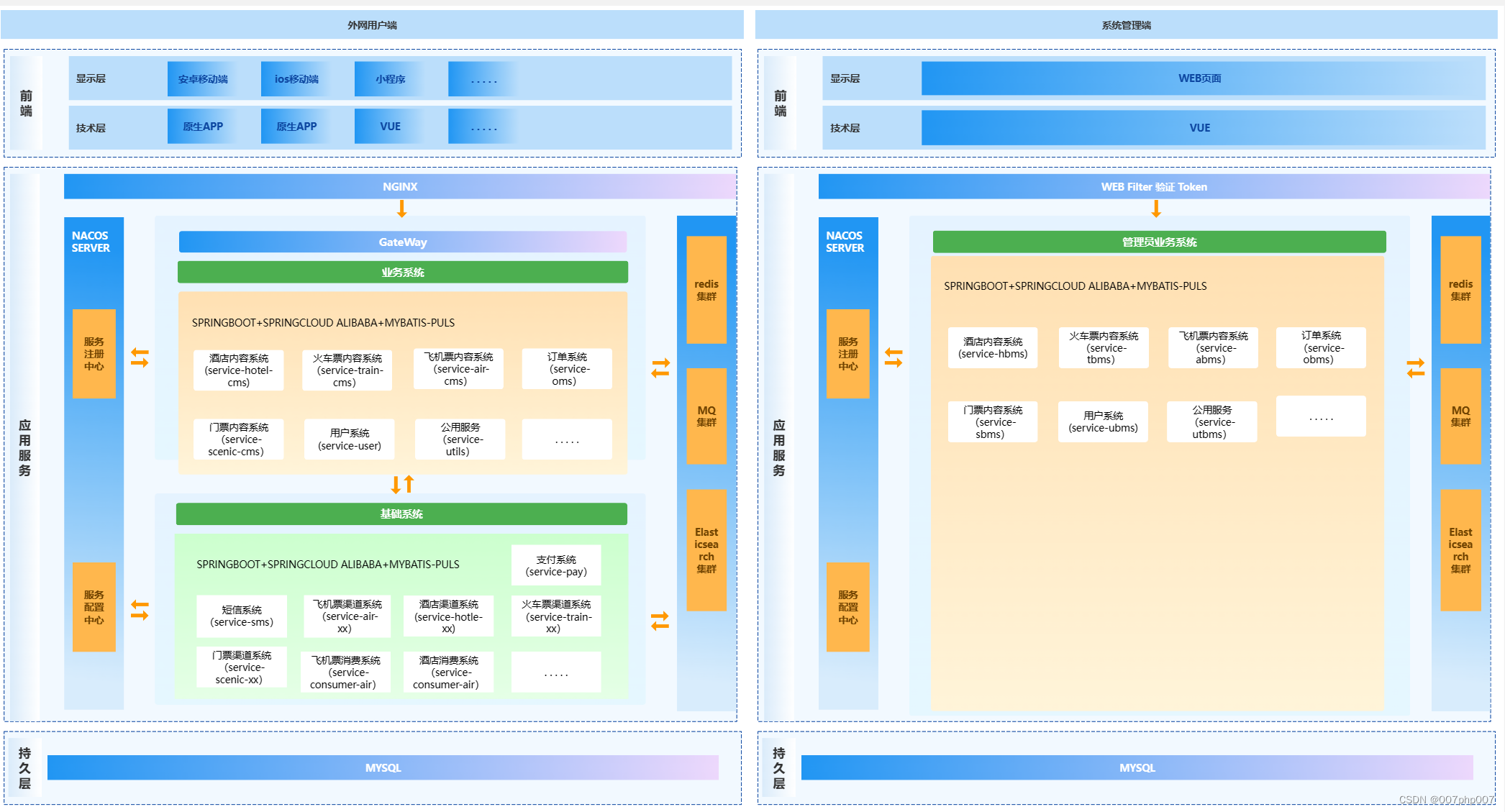
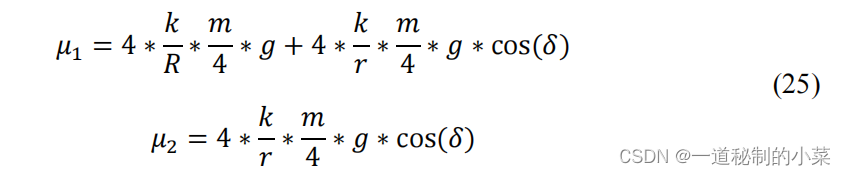目录
一、简介
二、运动学模型分析
1. 逆运动学方程
2. 正运动学方程
三、动力学模型
四、广泛运动学模型
一、简介
参考文献https://www.geometrie.tugraz.at/gfrerrer/publications/MecanumWheel.pdf
移动机器人的运动学模型是为了解决小车的正向运动学和逆向运动学问题,即我们需要知道小车的移动平台与其移动装置之间的关系,对于Mecanum模型,运动学模型表示平台速度与每个轮子旋转速度之间的关系。
移动机器人的动态模型可估算外力因素对移动平台运动的影响,并可计算出移动平台运动所需的推力和电机扭矩。
二、运动学模型分析
由上述文献我们得到下面的公式,该公式可以推导任何矩形多轮全方位平台的运动学模型
其中: - 为移动小车第n个全向轮的角速度 rad/s;
- R- 为车轮半径,米;
- 𝛿 - 全方位滚轮辊筒的倾角,度;
- 𝛼 - 车轮相对于平台的倾斜角,度;
- 𝑎𝑥,𝑎𝑦 - 车轮中心相对于平台几何中心的坐标,米;
- 𝑣𝑥, 𝑣𝑦 - 移动小车的线速度,米/秒;
- 𝜔 – 移动小车的角速度,弧度/秒。
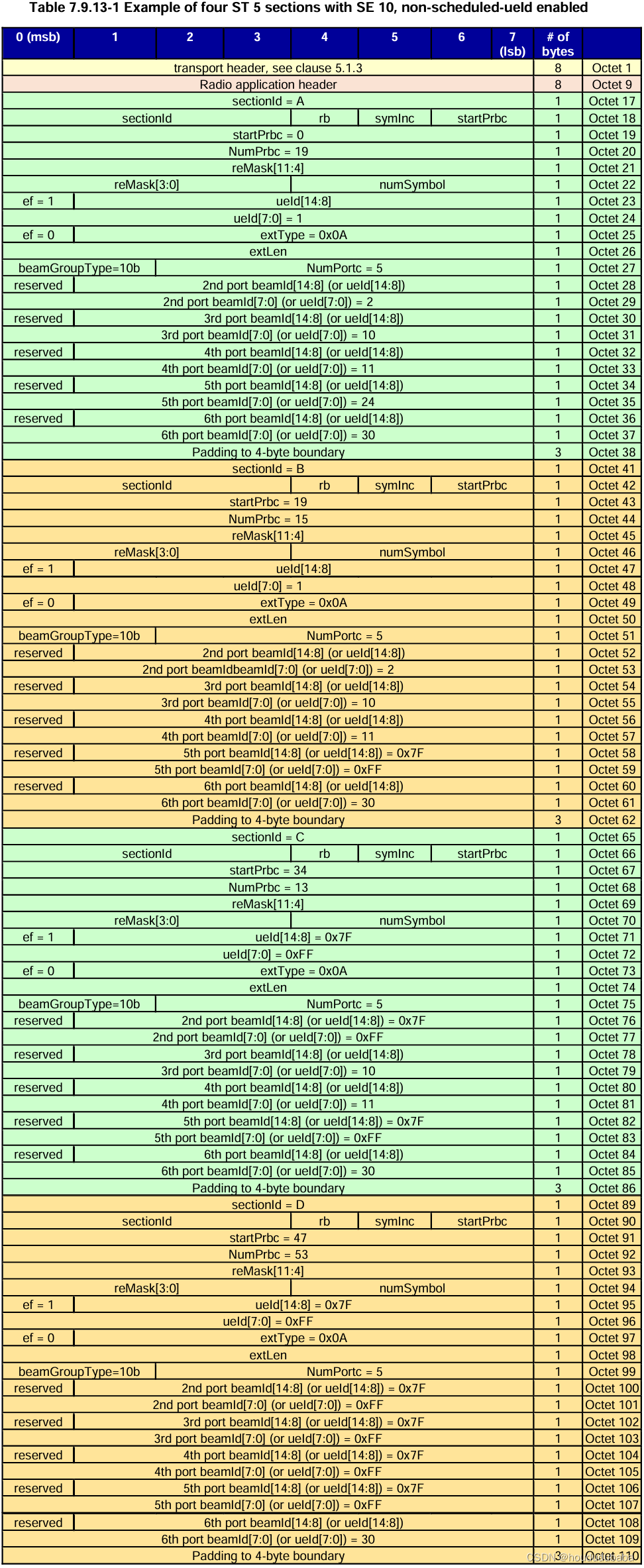
一般的麦克纳姆轮移动机器人的车轮倾斜参数,即 𝛼 = 0,将式 (1) 转化为式 (2),方法是将 sin(𝛿) 放入普通括号中。将 sin(𝛿) 插入公共括号。
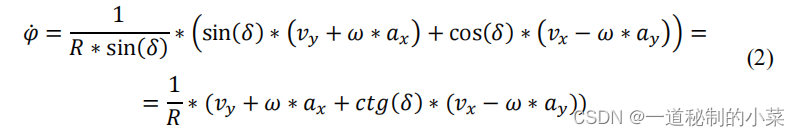
为了方便起见,我们将放入括号内,最终得到(3)
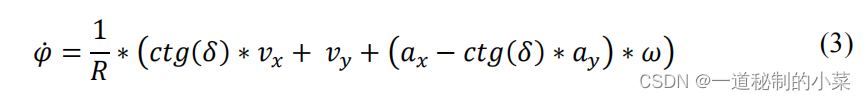 下图表示移动小车的平台 ,其中L和I分别表示小车平台尺寸的一半;轮子则表示滚轮与底面接触的斜度。
下图表示移动小车的平台 ,其中L和I分别表示小车平台尺寸的一半;轮子则表示滚轮与底面接触的斜度。
接下来我们指定万向轮中心的坐标及其滚轮的角度
- 轮1:𝑎𝑥 = -l ; 𝑎y = L ; 𝛿 = 45°
- 轮2:𝑎𝑥 = -l ; 𝑎y = L ; 𝛿 = 45°
- 轮3:𝑎𝑥 = -l ; 𝑎y = L ; 𝛿 = 45°
- 轮4:𝑎𝑥 = -l ; 𝑎y = L ; 𝛿 = 45°
将上述数值代入公式 (3),我们可以得到由每个车轮的角速度组成的方程组 (4)。
即为所求得的逆运动学模型
1. 逆运动学方程
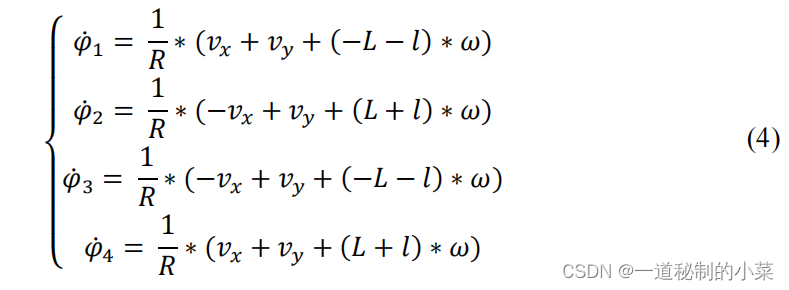
让我们将得到的方程以矩阵形式写成 (5),其中 K 是系数矩阵,行是系统 (4) 中每个车轮的系数,列是相应的速度𝑣𝑥、𝑣𝑦 和 𝜔。
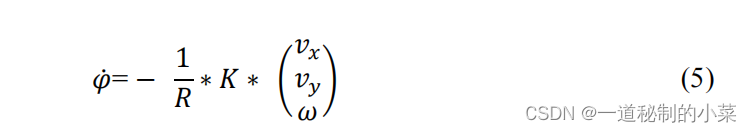
其中矩阵K如下所示:
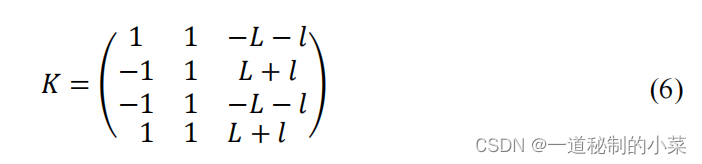
将方程 (4) 的所有方程相加,并按照相应变量进行分组,我们可以写出方程 (7),这就是该移动小车正运动学问题的解。
2. 正运动学方程
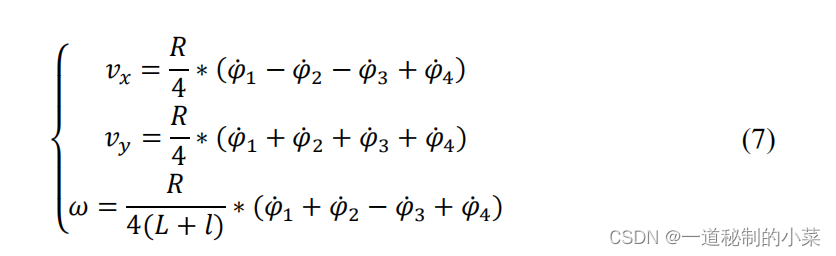
三、动力学模型
根据之前我们推导的运动学模型,我们来考虑移动小车沿 OY 轴的运动。根据方程 (7) ,为了使平台沿 OY 轴运动,四个车轮的旋转方向必须相同,并且必须是顺时针方向。
为了建立简化动态模型,将考虑作用在每个车轮上的以下力:牵引力、车轮滚动摩擦力、滚筒滚动摩擦力。这些力的矢量排列如下图所示。
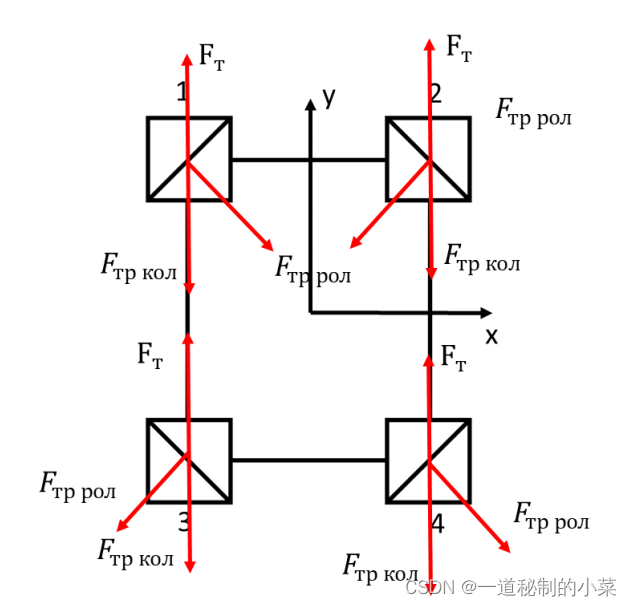
- Fт – 电机牵引力;(牵引力的方向与小车运动方向相同)
- Fтр кол– 车轮滚动摩擦力(车轮的滚动摩擦力与小车运动方向相反);
- Fтр рол– 滚轮滚动摩擦力(滚轮的滚动摩擦力与滚筒垂直,且方向与旋转方向相反);
在上图的基础上,让我们根据牛顿第二定律在 OY 轴上的投影建立一个方程(9)。
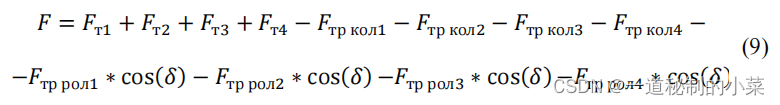
根据公式(7),对于沿OY轴的运动,轮子的转速必须相同,并且还假设整个移动平台的质量分布均匀地发生在每个轮子上,可以说,每个车轮考虑的所有力都是相等的,即:
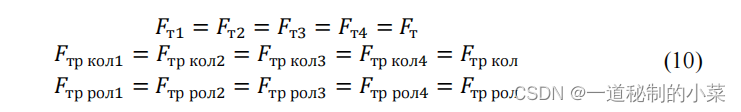
因此,通过牛顿第二定律我们可以得到公式(11)

接下来有移动小车受力公式和滚动摩擦力公式(12):

- m 是移动小车的质量,千克;
- a - 移动平台的加速度,m/c2;
- k - 滚动摩擦系数;
- N - 反作用力
反作用力由下列公式确定:

- 𝑚1为平台每一个轮子的质量,kg;
- 𝑔——自由落体加速度,m/s2。
假设小车的质量均匀分布在轮子之间,那么我们可以假设: 𝑚1 =𝑚/4,则滚动摩擦力的公式由(12)转换为(14)。

考虑到上述所有公式,我们写出完整的牛顿第二定律方程(15)。
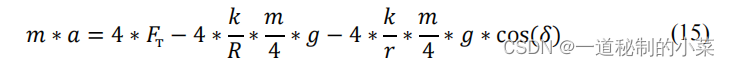
其中r是滚轮的半径,m。
通过上述方程,我们可以通过方程(16)来表达发动机的牵引力:
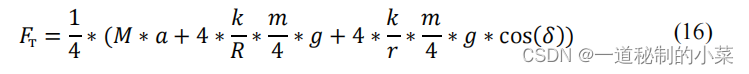
现在我们用公式(17)计算每个电机轴上的扭矩:

四、广泛运动学模型
为了推导轮子扭矩与机器人速度之间的关系,我们推导了移动小车沿 X 轴和 Y 轴移动时的广义牵引力的公式。
为此,我们用公式(17)表示牵引力的值,并根据运动学模型的公式(7)取总力矩与车轮的转速成正比。

其中𝑀𝑖是平台第i个轮子的转动力矩,N*m。
将沿OY轴移动时的广义牵引力的结果代入式(15)中进行变换。 结果我们有(Ftx = 0):
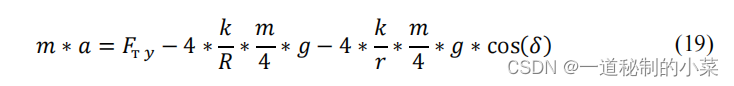
让我们对所得公式进行变换,将加速度视为沿 OY 轴运动速度的导数。
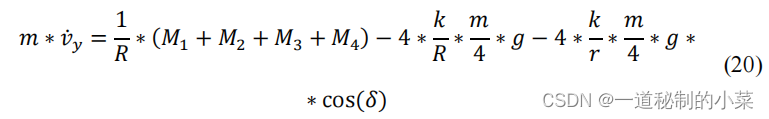
用常数系数 𝜇1 表示滚动摩擦力的影响,由式(20)得到移动平台速度对轮子扭矩的关系:
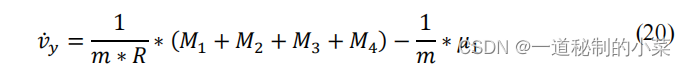
接下来我们可以类似的表达沿着X轴运动之间的关系 (下图为小车沿着X轴进行的运动分析)
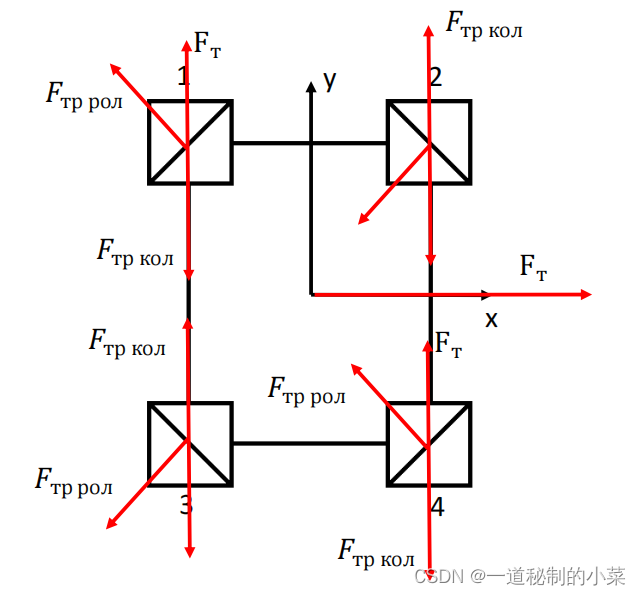
从图中可以看出,车轮的摩擦力不影响沿OX轴的运动,因此,对于该运动,方程(15)采用(21)的形式。
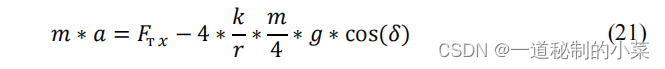
我们对所得公式(21)进行变换,将加速度设为沿 OX 轴运动速度的导数。
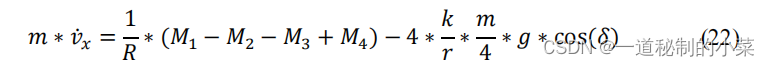
用常数系数 𝜇2 表示滚动摩擦力的影响,我们得到了移动小车速度对车轮扭矩的依赖关系。
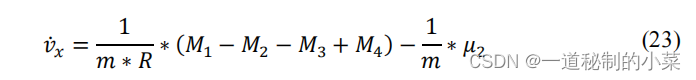
因此,一般动态模型采用形式如下公式(24)
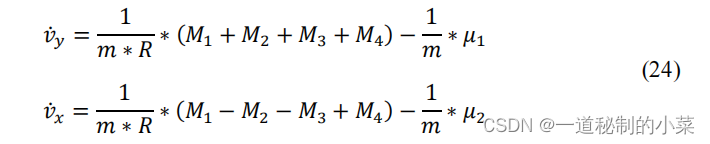
系数𝜇1和𝜇2由公式(25)确定。