文章目录

• 1、一和零
• 2、盈利计划
• 3、组合总和 Ⅳ
• 4、不同的二叉搜索树(卡特兰数)

1、一和零

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int len=strs.size();
        vector<vector<int>> dp(m+1,vector<int>(n+1));

        for(int i=1;i<len+1;i++)
        {
            int a=0,b=0;
            for(auto &e:strs[i-1])
            {
                if(e=='0')
                    a++;
                else
                    b++;
            }
            for(int j=m;j>=a;j--)//从大往小，原因是他是需要上一层的数据
            {
                for(int k=n;k>=b;k--)
                    dp[j][k]=max(dp[j][k],dp[j-a][k-b]+1);
            }
        }
        return dp[m][n];
    }
};

2、盈利计划

集团里有 n 名员工，他们可以完成各种各样的工作创造利润。
第 i 种工作会产生 profit[i] 的利润，它要求 group[i] 名成员共同参与。如果成员参与了其中一项工作，就不能参与另一项工作。
工作的任何至少产生 minProfit 利润的子集称为 盈利计划 。并且工作的成员总数最多为 n 。
有多少种计划可以选择？因为答案很大，所以 返回结果模 10^9 + 7 的值。

class Solution {
public:
    int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {
        const int MOD=1e9+7;
        int len=group.size();
        vector<vector<int>> dp(n+1,vector<int>(minProfit+1));

        for(int i=0;i<=n;i++)
            dp[i][0]=1;
        
        for(int i=1;i<len+1;i++)
        {
            for(int j=n;j>=group[i-1];j--)
            {
                for(int k=minProfit;k>=0;k--)
                {
                    dp[j][k]+=dp[j-group[i-1]][max(0,k-profit[i-1])];
                    dp[j][k]%=MOD;
                }
            }
        }
        return dp[n][minProfit];
    }
};

3、组合总和 Ⅳ

给定一个由 不同 正整数组成的数组 nums ，和一个目标整数 target 。请从 nums 中找出并返回总和为 target 的元素组合的个数。数组中的数字可以在一次排列中出现任意次，但是顺序不同的序列被视作不同的组合。
题目数据保证答案符合 32 位整数范围

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        vector<double> dp(target+1);
        dp[0]=1;
        for(int i=1;i<target+1;i++)
        {
            for(auto& e:nums)
            {
                if(i>=e)
                    dp[i]+=dp[i-e];
            }
        }
        return dp[target];
    }
};

4、不同的二叉搜索树(卡特兰数)

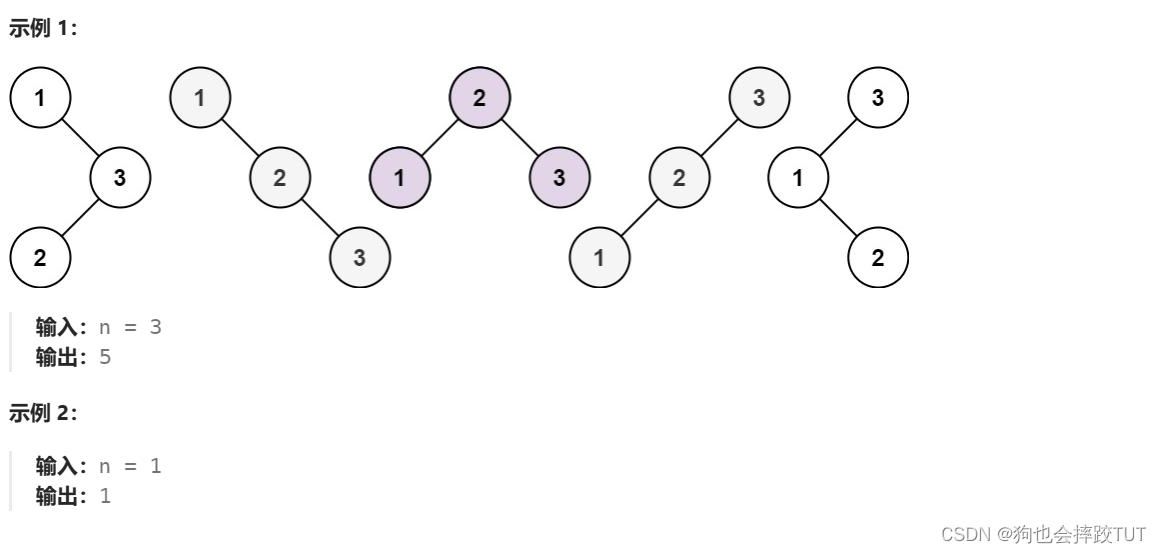
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n+1);
        dp[0]=1;
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=i;j++)
                dp[i]+=dp[j-1]*dp[i-j];
        }
        return dp[n];
    }
};