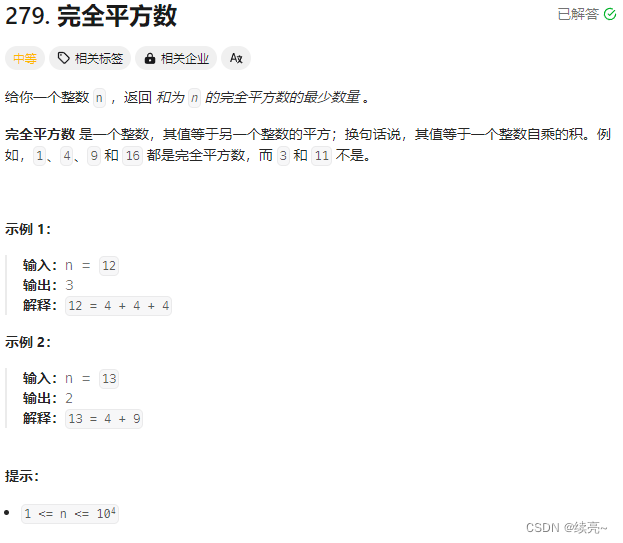
思路 

第一种递归方式：

 public static int numSquares3(int n) {
        if (n<=2){
            return n;
        }
        return process(n);
    }

    private static int process(int rest) {
       if (rest<=0){
           return 0;
       }
        int min=rest;
        for (int i = 2; i*i <=rest ; i++) {
            int count=rest/(i*i);
            for (int j = 1; j <=count; j++) {
                min=Math.min(j+process(rest-i*i),min);
            }
        }
       return min;
    }

第二种动态规划：依照递归方式我们可以知道状态转移方程

动态规划思路

1. 定义DP数组：dp[i] 表示整数 i 最少可以由多少个完全平方数相加组成。
2. 初始化：对于任意整数 i，最坏的情况是 i 由 i 个 1 组成，因此 dp[i] 初始化为 i。
3. 状态转移：对于每个 i，遍历所有可能的完全平方数 j*j（j*j <= i），更新 dp[i] 为 dp[i] 和 dp[i-j*j] + 1 中的较小值。其中 +1 是因为 j*j 是参与组成 i 的一个完全平方数。
4. 边界条件：dp[0] 应为 0，因为0不需要任何数字就能表示。

代码如下：

 public static int numSquares(int n) {
        if (n<=2){
            return n;
        }
        int[] dp = new int[n + 1];
        dp[1]=1;
        dp[2]=2;
        for (int i =3; i <=n; i++) {
            //最坏情况下 都是1 组成
            dp[i]=i;
            for (int j = 2; j*j <=i ; j++) {
                //直接给 j*j 赋值
                dp[j*j]=1;
                //两个部分组成 dp[i-j*j]和dp[j*j]=>dp[i-j*j]+1
                dp[i]=Math.min(dp[i],dp[i-j*j]+dp[j*j]);
            }
        }
        return dp[n];
    }