LLaMA详细解读

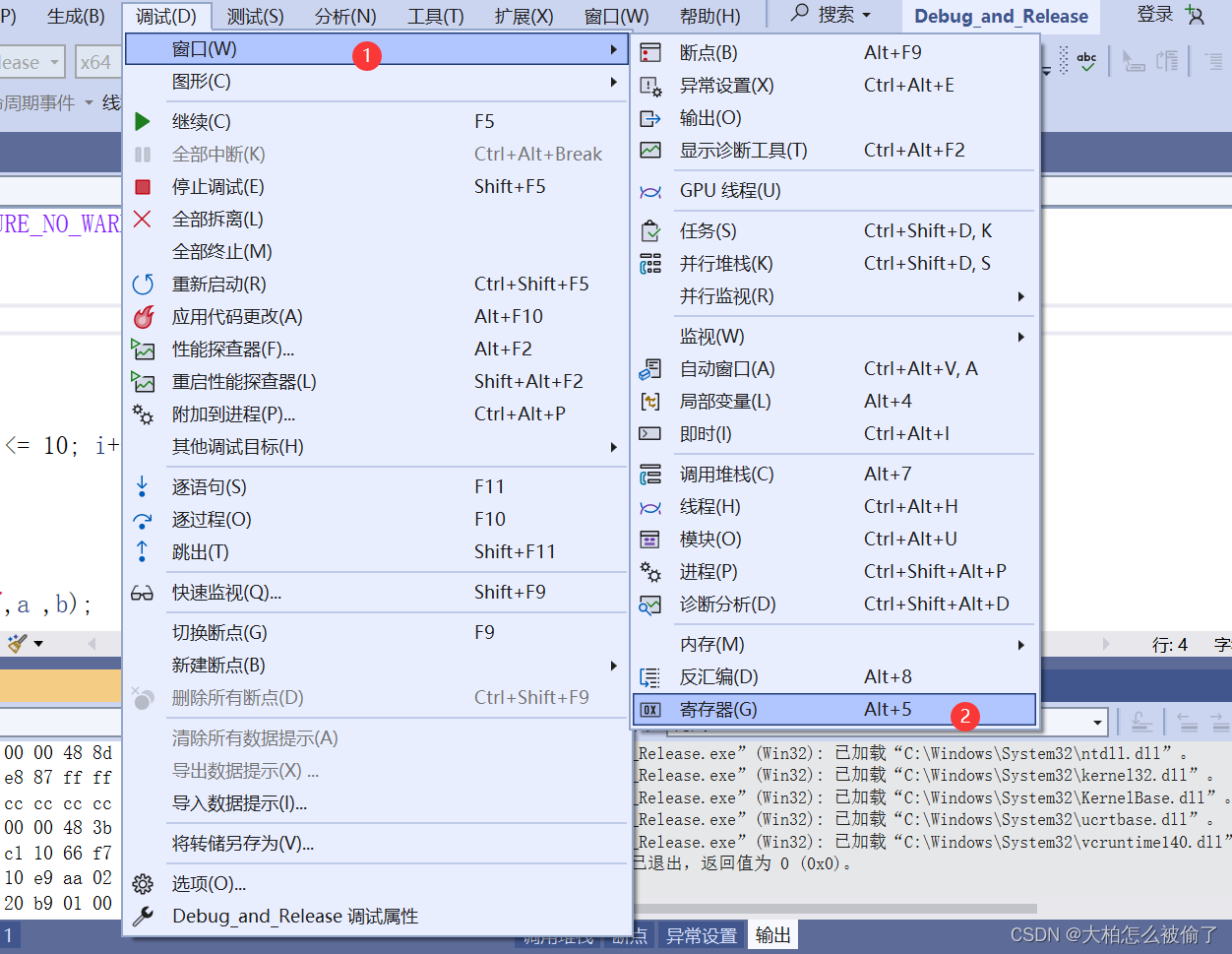
LLaMA 是目前为止，效果最好的开源 LLM 之一。精读 LLaMA 的论文及代码，可以很好的了解 LLM 的内部原理。本文对 LLaMA 论文进行了介绍，同时附上了关键部分的代码，并对代码做了注释。

摘要

LLaMA是一个系列模型，模型参数量从7B到65B。在大部分的任务上，LLaMA-13B强于GPT-3(175B)。LLaMA-65B的性能，可以和最好的LM相媲美，如Chinchilla-70B 和 PaLM-540B。

一、引言

一般而言，模型越大，效果越好。然而有文献指出[1]，当给定计算量的预算之后，最好的performance，并不是最大的模型，而是在一个小模型上用更多的数据进行训练。针对给定的计算量预算，scaling laws可以计算如何选择数据量的大小和模型的大小。然而这忽略了inference的预算，而这一点在模型推理时非常关键。当给定一个模型performance目标之后，最好的模型不是训练最快的模型，而是推理最快的模型。尽管在这种情况下，训练一个更大的模型成本会更低。

文献[2]中推荐，训练一个 10B 的模型，需要 200B 的 tokens，而本文的实验发现，一个7B的模型，经过 1T tokens 训练之后，performance 仍然在增加。本文的目标在于，通过在超大规模的数据上训练，给出一系列可能最好 performance 的 LLM。

二、预训练数据

2.1 数据集

一共有1.4T的tokens，大部分的训练数据都只用了一次，除了Wikipedia 和 Books 使用了大概2个epochs。

Pre-training data

2.2 tokenizer

使用byte pair encoding (BPE) 算法，使用的是Sentence-Piece的实现。所有数字被拆分为单独的digit，所有未知的UTF-8 字符，回退到字节来进行分解。因此，LLaMA 可以通过byte 的方式，构造出很多不在 vocab 中的字符，从而也具有较好的多语言能力。

三、网络结构改进

使用了基于transformer的架构，并做了如下3点改进：

3.1 Pre-normalization

为了提高训练的稳定性，对每个transformer层的输入进行归一化，而不是输出进行归一化。

同时，使用 RMS Norm 归一化函数。RMS Norm 的全称为 Root Mean Square layer normalization。与 layer Norm 相比，RMS Norm的主要区别在于去掉了减去均值的部分，计算公式为：

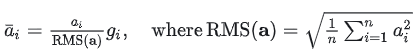
RMS Norm 的作者认为这种模式在简化了Layer Norm 的计算，可以在减少约 7%∼64% 的计算时间[3]。

class LlamaRMSNorm(nn.Module):
    def __init__(self, hidden_size, eps=1e-6):
        """
        LlamaRMSNorm is equivalent to T5LayerNorm
        """
        super().__init__()
        self.weight = nn.Parameter(torch.ones(hidden_size))
        self.variance_epsilon = eps

    def forward(self, hidden_states):
        input_dtype = hidden_states.dtype
        variance = hidden_states.to(torch.float32).pow(2).mean(-1, keepdim=True)
        hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon)

        return (self.weight * hidden_states).to(input_dtype)

3.2 SwiGLU

使用SwiGLU替代了ReLU作为激活函数。和PaLM中不同，维度采用而不是 4𝑑 。

SwiGLU 在论文[4] 中提出，相比于其他的激活函数变体，可以取得 log-perplexity 的最优值（和 GEGLU 并列）。

GLU Variants Improve Transformer

SwiGLU 及几种类似变体的计算公式如下：

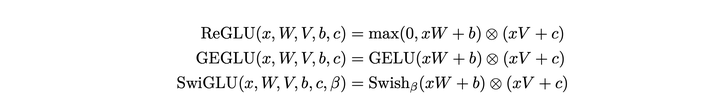
其中，。代码如下：

class LlamaMLP(nn.Module):
    def __init__(
        self,
        hidden_size: int,
        intermediate_size: int,
        hidden_act: str,
    ):
        super().__init__()
        self.gate_proj = nn.Linear(hidden_size, intermediate_size, bias=False)
        self.down_proj = nn.Linear(intermediate_size, hidden_size, bias=False)
        self.up_proj = nn.Linear(hidden_size, intermediate_size, bias=False)
        # config 中 hidden_act = 'silu'
        # 'silu' 和 'swish' 对应的激活函数均为：SiLUActivation 
        # https://github.com/huggingface/transformers/blob/717dadc6f36be9f50abc66adfd918f9b0e6e3502/src/transformers/activations.py#L229
        self.act_fn = ACT2FN[hidden_act]

    def forward(self, x):
        # 对应上述公式的 SwiGLU
        return self.down_proj(self.act_fn(self.gate_proj(x)) * self.up_proj(x))

从代码可以看到 LlamaMLP 中一共有 3 个 Linear 层，原因就在于 SwiGLU 激活函数比类似 ReLU 的激活函数，需要多一个 Linear 层进行门控。

3.3 RoPE

RoPE 的核心思想是“通过绝对位置编码的方式实现相对位置编码”，可以说是具备了绝对位置编码的方便性，同时可以表示不同 token 之间的相对位置关系。[5] 不同于原始 Transformers 论文中，将 pos embedding 和 token embedding 进行相加，RoPE 是将位置编码和 query （或者 key）进行相乘。具体如下：

Rotary Position Embedding

其中，左侧的矩阵 𝑅𝑚 表示位置第 𝑚 个位置的位置编码，右侧的向量 𝑞𝑖 表示对应位置的 query 向量。两者相乘，即可得到增加了位置信息的 query （或者 key）。由于 𝑅𝑚 的稀疏性，上述矩阵乘法可以等价于：

Rotary Position Embedding 的简化实现

其中 ⊗ 是逐位对应相乘，。

RoPE的代码实现如下[6]：

# 代码增加了注释，可以看到和原始公式的对应关系。
class LlamaRotaryEmbedding(torch.nn.Module):
    def __init__(self, dim, max_position_embeddings=2048, base=10000, device=None):
        super().__init__()
        # 此处 inv_freq 对应公式中的 theta
        inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2).float().to(device) / dim))
        self.register_buffer("inv_freq", inv_freq)

        self.max_seq_len_cached = max_position_embeddings
        t = torch.arange(self.max_seq_len_cached, device=self.inv_freq.device, dtype=self.inv_freq.dtype)
        # 此处 freqs 对应公式中的 m * theta, t 对应公式中的 m，表示位置
        freqs = torch.einsum("i,j->ij", t, self.inv_freq)
        # Different from paper, but it uses a different permutation in order to obtain the same calculation
        # 此处和原始公式不同，theta_0 和 theta_0 不再相邻
        # 而是分在向量的前半部分和后半部分
        emb = torch.cat((freqs, freqs), dim=-1)
        dtype = torch.get_default_dtype()
        self.register_buffer("cos_cached", emb.cos()[None, None, :, :].to(dtype), persistent=False)
        self.register_buffer("sin_cached", emb.sin()[None, None, :, :].to(dtype), persistent=False)

    def forward(self, x, seq_len=None):
        # x: [bs, num_attention_heads, seq_len, head_size]
        if seq_len > self.max_seq_len_cached:
            self.max_seq_len_cached = seq_len
            t = torch.arange(self.max_seq_len_cached, device=x.device, dtype=self.inv_freq.dtype)
            freqs = torch.einsum("i,j->ij", t, self.inv_freq)
            # Different from paper, but it uses a different permutation in order to obtain the same calculation
            emb = torch.cat((freqs, freqs), dim=-1).to(x.device)
            self.register_buffer("cos_cached", emb.cos()[None, None, :, :].to(x.dtype), persistent=False)
            self.register_buffer("sin_cached", emb.sin()[None, None, :, :].to(x.dtype), persistent=False)
        # 大部分情况下，直接从这里返回
        return (
            self.cos_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
            self.sin_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
        )


def rotate_half(x):
    """Rotates half the hidden dims of the input."""
    # 此次和原始推导中不同，正负号不是间隔的，而是分前半部分和后半部分。但对于结果没有影响
    x1 = x[..., : x.shape[-1] // 2]
    x2 = x[..., x.shape[-1] // 2 :]
    return torch.cat((-x2, x1), dim=-1)


def apply_rotary_pos_emb(q, k, cos, sin, position_ids):
    # The first two dimensions of cos and sin are always 1, so we can `squeeze` them.
    cos = cos.squeeze(1).squeeze(0)  # [seq_len, dim]
    sin = sin.squeeze(1).squeeze(0)  # [seq_len, dim]
    cos = cos[position_ids].unsqueeze(1)  # [bs, 1, seq_len, dim]
    sin = sin[position_ids].unsqueeze(1)  # [bs, 1, seq_len, dim]
    # 对应上图中 RoPE 的简化计算
    q_embed = (q * cos) + (rotate_half(q) * sin)
    k_embed = (k * cos) + (rotate_half(k) * sin)
    return q_embed, k_embed

四、高效实现

加速训练：

使用了xformers库。
减少了activation checkpointing 中，重新计算 activation 的计算量。手动实现 transformer 层的反向传递函数，保存了计算成本高的 activations，例如线性层的输出。
通过使用 model parallelism 和 sequence parallelism 来减少显存的使用量。
尽可能地将 activations 的计算和GPU之间的通讯进行并行。

加速效果：

65B的模型，在2048个80G的A100 GPU上，可以达到380 tokens/sec/GPU的速度。训练1.4T tokens需要21天。

五、主要结果与结论

Massive Multitask LanguageUnderstanding

LLaMA-13B 优于 GPT-3，尽管只有1/10大小。 LLaMA-65B 是可以与 Chinchilla-70B 和 PaLM-540B 这种最佳的LLM相竞争的模型。经过微调之后，LLaMA的效果有显著的提升。

未来打算发布在更大的语料上预训练上的更大的模型，因为随着数据和模型的增大，可以看到 performance 的稳定提升。

优化器

LLaMA使用了AdamW优化器进行训练，优化器的超参数为 =0.9, =0.95

(关于AdamW这个大模型训练的优化器，可参考当前训练神经网络最快的方式：AdamW优化算法+超级收敛 | 机器之心[6])

下表为LLaMA不同参数大小模型的具体设置：

表2: LLaMA不同参数大小模型的具体设置

参数	维度（dim）	head个数	layer层数	学习率	batch size	token数量
6.7B	4096	32	32	3.0e−4	4M	1.0T
13.0B	5120	40	40	3.0e−4	4M	1.0T
32.5B	6656	52	60	1.5e−4	4M	1.4T
65.2B	8192	64	80	1.5e−4	4M	1.4T

训练结果

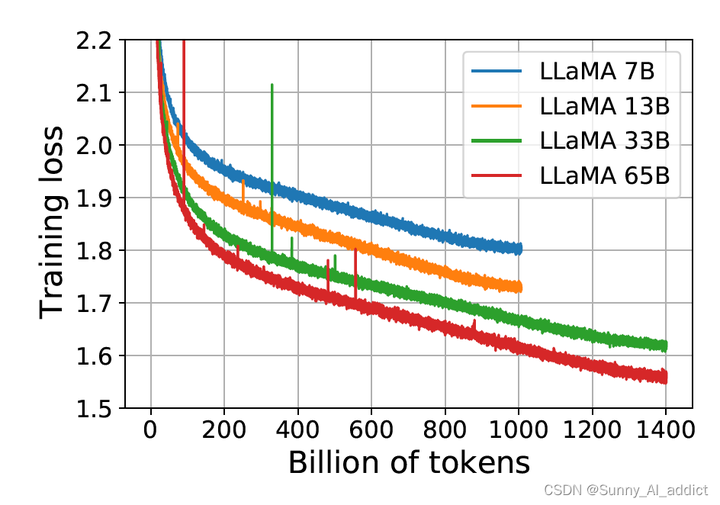
如下图所示，7B、13B、33B和65模型的训练损失均呈下降趋势，且在所有token上训练完后，loss仍没有收敛的趋势。因此，在此时，增加训练的token数量，仍然可以使模型继续学习。

（LLaMA2就是在此结论的基础上，使用了更多的token进行训练）

高效部署

研究团队做了一些优化来提高模型的训练速度：

因果多头注意的有效实现：使用因果多头注意的有效实现来减少内存使用和运行时间。该实现可在xformers库中获得，其灵感来自于固定激活值显存优化和FlashAttention。这是通过不存储注意力权重和不计算由于语言建模任务的因果性质而被掩盖的key/query分数来实现的。
激活重计算：为了进一步提高训练效率，通过检查点减少了在向后传递过程中重新计算的激活量。更准确地说，节省了计算成本高的激活，比如线性层的输出。这是通过手动实现transformer层的backward函数来实现的，而不是依赖于PyTorch的autograd。
模型并行和序列并行：为了从这种优化中充分受益，需要通过使用模型和序列并行来减少模型的内存使用。此外，还尽可能地重叠激活的计算和gpu之间通过网络的通信。

笔者NOTE：LLM的高效训练是LLM工程实现的基础，对于这部分，各位小伙伴还是需要深入地了解一下各种并行策略、因果多头注意的有效实现、激活重计算、混合精度训练。

参考

^Training Compute-Optimal Large Language Models https://arxiv.org/abs/2203.15556
^Training Compute-Optimal Large Language Models https://arxiv.org/abs/2203.15556
^Root Mean Square Layer Normalization https://arxiv.org/pdf/1910.07467.pdf
^GLU Variants Improve Transformer https://arxiv.org/pdf/2002.05202.pdf
^Transformer升级之路：2、博采众长的旋转式位置编码 Transformer升级之路：2、博采众长的旋转式位置编码 - 科学空间|Scientific Spaces
^transformers/src/transformers/models/llama/modeling_llama.py at main · huggingface/transformers · GitHub