前言
有人问过我,C++里的函数是否跟我们数学里的函数一样?于是,我就写下了这篇文章。
一、数学函数
1、一次函数
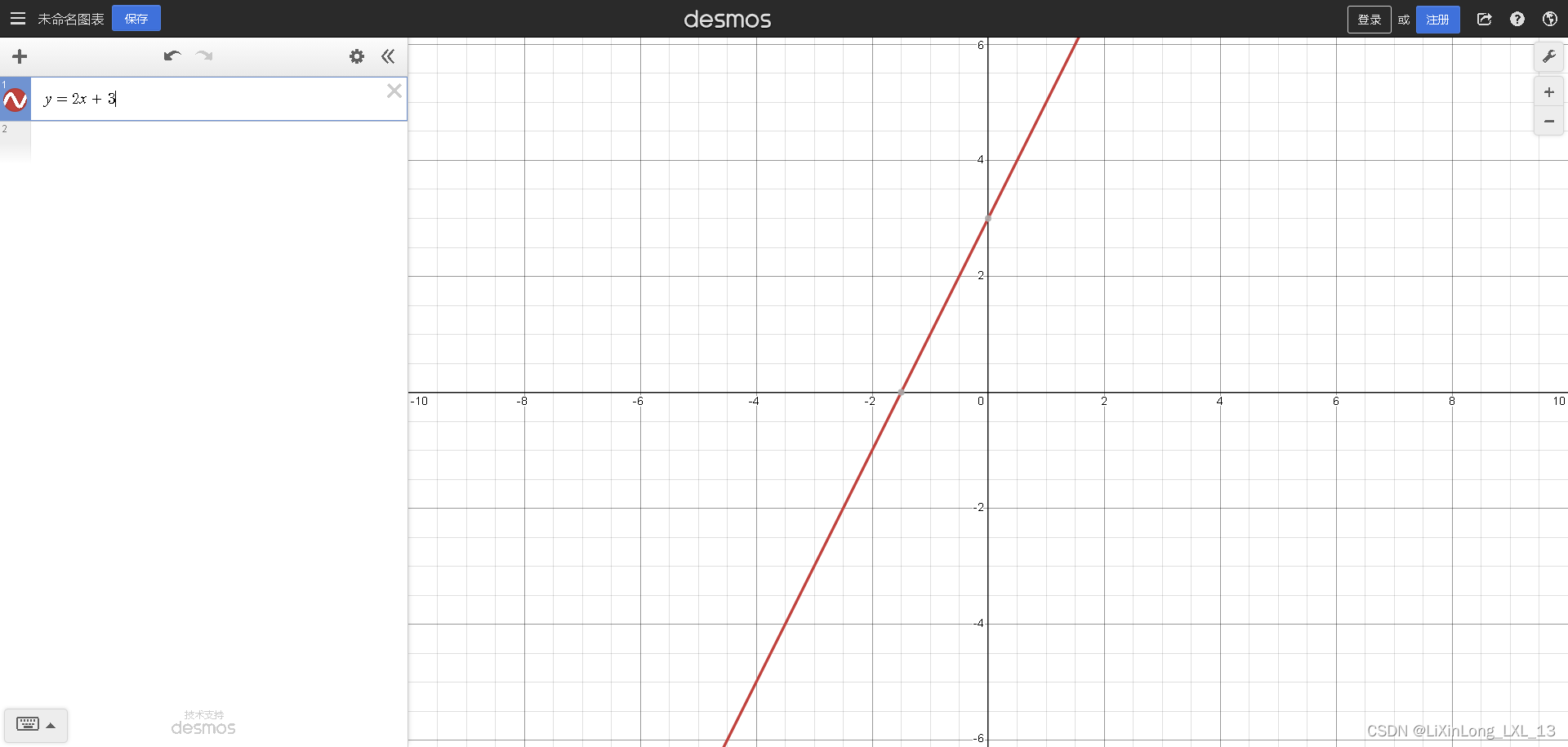
一次函数,也称为线性函数,是数学中函数的一种,通常表示为y=kx+b(其中k和b是常数,且k≠0),x是自变量,y是因变量。
一次函数的图像是一条直线,k决定了直线的斜率,即倾斜程度,b是直线与y轴的截距。当b=0时,一次函数简化为y=kx,此时称为正比例函数。一次函数在数学和现实生活中有广泛的应用,它可以描述许多随时间或其他因素均匀变化的现象。
比如下图,是一个一次函数。
2、二次函数
二次函数(quadratic function)的基本表示形式为y=ax²+bx+c(a≠0)。二次函数最高次必须为二次, 二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。
二次函数表达式为y=ax²+bx+c(且a≠0),它的定义是一个二次多项式(或单项式)。
如果令y值等于零,则可得一个二次函数。该方程的解称为方程的根或函数的零点。
比如下图:
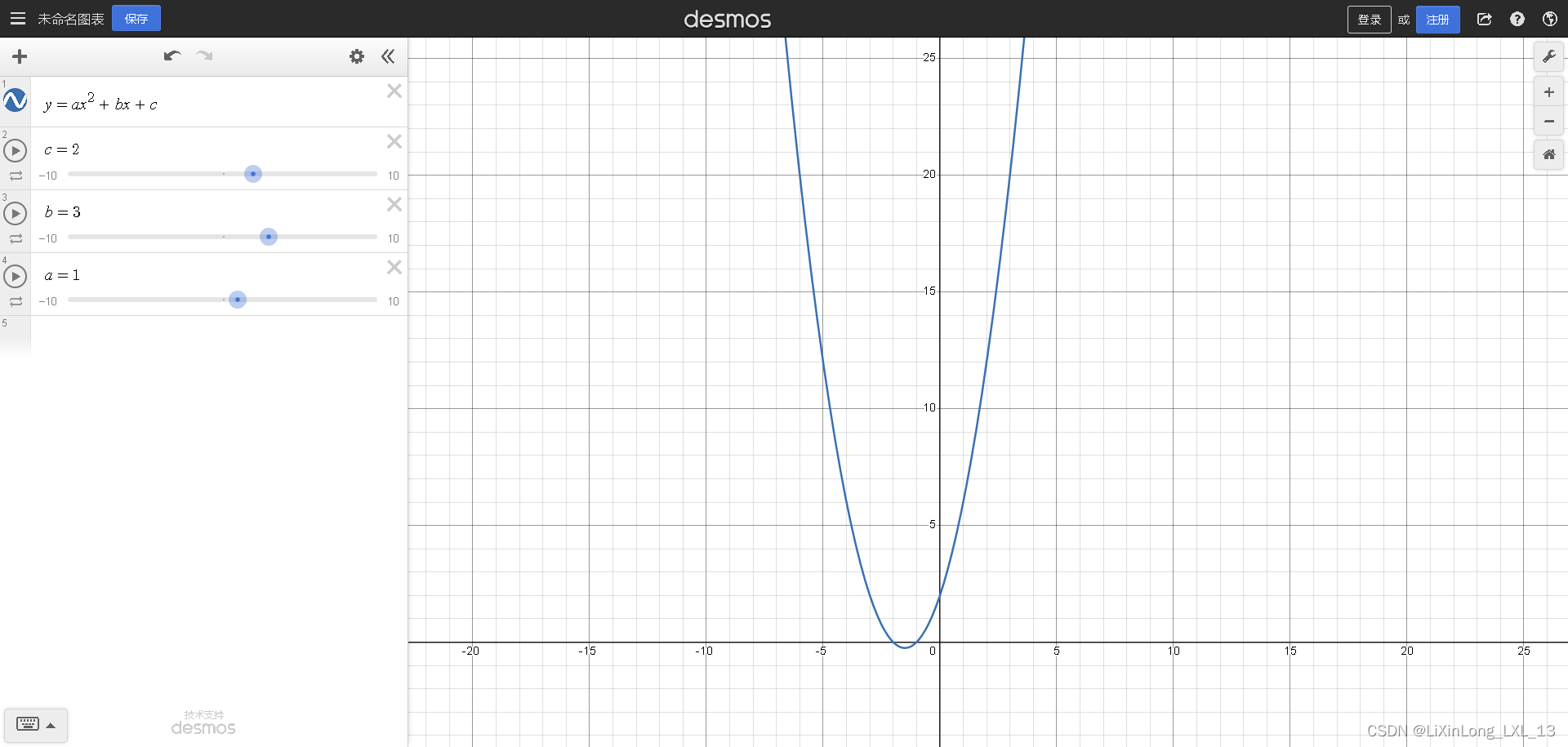
二次函数具有对称性、单调性。
a>0,开口向上;a<0,开口向下。a的绝对值越大,抛物线越小。
a>0,x>h时,y随着x的值增大而增大;a<0,x>h时,y随着x的增大而减小。
3、指数函数
指数函数是一类重要的数学函数,其形式为 f(x) = a^x,其中 a 是底数,x 是指数。指数函数定义在实数范围内,底数 a 必须是正数且不等于 1。
当底数 a 大于 1 时(例如 a = 2, 3, e 等),函数 f(x) = a^x 随着 x 的增大而增大,即函数图像在实数轴上是上升的。
当底数 a 在 0 和 1 之间时(例如 a = 1/2, 1/3 等),函数 f(x) = a^x 随着 x 的增大而减小,即函数图像在实数轴上是下降的。
特别地,当底数 a 等于自然对数的底数 e(约等于 2.71828)时,该函数称为自然指数函数,通常表示为 exp(x) 或 e^x。
指数函数在数学、物理、工程、经济等领域有广泛的应用。例如,在复利计算、细菌生长、放射性衰变等情境中,指数函数都是重要的数学模型。
指数函数如下

4、对数函数
对数函数是一类重要的数学函数,它描述了指数函数的反操作。对数函数以幂的形式定义,即如果 (a^x = N)(其中 (a) 是底数,(x) 是指数,(N) 是真数),那么对数函数表示为。
对数函数的一般形式为,其中 (a) 是底数,(x) 是真数。对数函数定义在 (x > 0) 的范围内,底数 (a) 必须是正数且
。对数函数和指数函数是互逆的,即
和
。
对数函数有一些重要的性质,例如:
- 换底公式:
,其中 (c) 是另一个正数且
。
- 对数的乘积转化为加法:
。
- 对数的商转化为减法:
。
- 对数的幂转化为乘法:
。
对数函数在数学、科学、工程等领域有广泛的应用。例如,在物理学中,对数函数用于描述声音的响度级别(分贝);在经济学和金融学中,对数函数用于复利计算和资产增长率的描述;在生物学和生态学中,对数函数用于描述种群增长等。
对数函数有两种特殊情况:
- 自然对数:当底数 (a) 为自然常数 (e)(约等于 2.71828)时,对数函数称为自然对数,记作
或
。
- 常用对数:在科学和工程中,以 10 为底的对数称为常用对数,记作
或
。
对数函数和对数表在历史上曾被广泛使用,尤其是在没有电子计算器的时候,人们使用对数表来执行乘法和除法运算。现在,对数函数在计算机科学和数学软件中也扮演着重要角色。
二、编程(C++)函数
1、电脑自带函数
我在《用C++求绝对值的几种方法》 这一篇文章中就有提到过,如swap(x,y)、min(x,y)、max(x,y) ......
这些我们是可以直接使用的。它给我们带来了巨大的方便。
比如说swap()函数吧,按照原理,我们交换两个数要通过第三方变量进行交换。
int a = 2 , b = 3;
int temp = a;
a = b;
b = temp;那么,是用swap()就比较方便了
int a = 2 , b = 3;
swap (a , b);有时候也可以套用函数,如:我们要求出三个数的最大值。那使用max()是最好不过了。
#include<bits/stdc++.h>
using namespace std;
int main(){
int a, b, c;
cin >> a >> b >> c;
cout<< max(a, max(b, c));
return 0;
}
2、非电脑自带函数
这些函数需要我们自己写,有些函数可直接使用。以下是函数的基本框架。
在C++中,函数的定义是指创建一个函数的具体实现,包括函数名、返回类型、参数列表以及函数体。函数的定义必须在一个源文件中,而不能在声明中进行。
函数定义的一般形式如下:
返回类型 函数名(参数列表) {
// 函数体
// 执行的代码
return 返回值;
}(一)有返回值函数
有返回值的函数是将某个数进行一些处理所得到的结果。
下面是一个简单的C++函数定义示例:
// 函数定义:计算两个整数的和
int add(int a, int b) {
return a + b;
} 在这个例子中,add 是函数名,它接受两个 int 类型的参数,返回它们的和。函数的定义以关键字 int 开始,后面是函数名 add 和参数列表 (int a, int b),接着是函数体,最后是返回语句 return a + b;。
递推(与函数息息相关)
在C++编程中,递推(Recursion)是一种解决问题的方法,它涉及到函数直接或间接地调用自身来解决较小规模的子问题,然后将这些子问题的解组合起来以解决原问题。递推通常用于解决可以分解为相似子问题的问题,这些子问题的解决方案是构建原问题解决方案的基础。
递推与迭代不同,迭代使用循环来逐步逼近解,而递推则是通过函数调用栈来逐步求解。递推通常更加简洁和易于理解,但也可能导致更高的计算复杂性和内存消耗,因为它需要维护函数调用栈。
递推的一个关键点是必须有一个或多个基本情况(Base Cases),这些情况是递归可以直接解决而不需要再次调用自身的。当递归调用到达这些基本情况时,它会停止并返回结果,然后这个结果会被用来构建更大问题的解。
下面是一个简单的C++递推函数示例,用于计算阶乘:
#include <iostream>
using namespace std;
// 递推函数用于计算阶乘
int factorial(int n) {
// 基本情况
if (n == 0 || n == 1) {
return 1;
}
// 递推情况
else {
return n * factorial(n - 1);
}
}
int main() {
int number;
cin >> number;
cout << "此数的阶乘是:" << factorial(number) << endl;
return 0;
} factorial 函数是一个递推函数,它接受一个整数 n 并返回 n 的阶乘。当 n 是0或1时,函数返回1,这是基本情况。否则,它递归地调用自身来计算 (n-1) 的阶乘,然后将结果乘以 n。
需要注意的是,对于非常大的 n,这个递推函数可能会导致栈溢出,因为函数调用栈可能变得非常深。在实际应用中,递推函数需要谨慎使用,特别是当涉及到大量递归调用时。
(二)无返回值函数
无返回值的函数,是指那些不返回任何值的函数。这种函数通常用于执行某种操作,例如修改全局变量、打印输出、调用其他函数等,而不是计算并返回一个值。
无返回值函数的返回类型被指定为 void。
void 关键字表示函数不返回任何值。
无返回值函数的定义形式如下:
void 函数名(参数列表) {
// 函数体
// 执行的代码
}下面是一个无返回值函数的例子,该函数用于打印一条消息到控制台:
#include <iostream>
using namespace std;
// 无返回值函数:打印消息到控制台
void printMessage() {
cout << "Hello, world!" << endl;
}
int main() {
printMessage(); // 调用无返回值函数
return 0;
} 在这个例子中,printMessage 函数不接受任何参数(参数列表为空),并且没有返回任何值(返回类型为 void)。当调用 printMessage() 时,它会执行函数体内的代码,将字符串 "Hello, world!" 打印到控制台。
无返回值函数在C++编程中非常常见,它们用于执行各种任务,如设置配置、执行初始化操作、处理用户输入、更新数据结构等。
三、数学函数与C++函数的异同点
共同点:
- 目的:二者都是为了根据给定的输入(或称为参数)来计算并返回一个输出(或称为返回值)。
- 关系映射:数学函数和C++函数都可以视为一种从输入到输出的映射关系。
差异点:
- 严格性:数学函数通常更为严格。在数学上,同一个输入必须总是产生相同的输出,即函数是确定的。相比之下,C++函数允许在相同的输入下产生不同的输出,尤其是当函数包含随机性或依赖于外部状态时。
- 应用领域:数学函数通常用于描述自然规律、归纳总结和做出预测。而C++函数主要用于编程,用于处理数据、执行计算任务和组织代码逻辑。
- 表示方法:数学函数通常以数学公式或表达式表示,而C++函数则是以程序代码的形式实现。
- 性质:数学函数可能具有特定的性质,如有界性、单调性、奇偶性和周期性。而C++函数则可能具有其他特性,如内联函数、递归函数等。
- 错误处理:在数学中,函数通常不处理错误或异常情况。然而,在C++中,函数可能需要处理各种错误条件,如无效输入或资源不足等。
综上所述,数学函数和C++函数在目的和关系映射方面有共同点,但在严格性、应用领域、表示方法、性质和错误处理等方面存在差异。