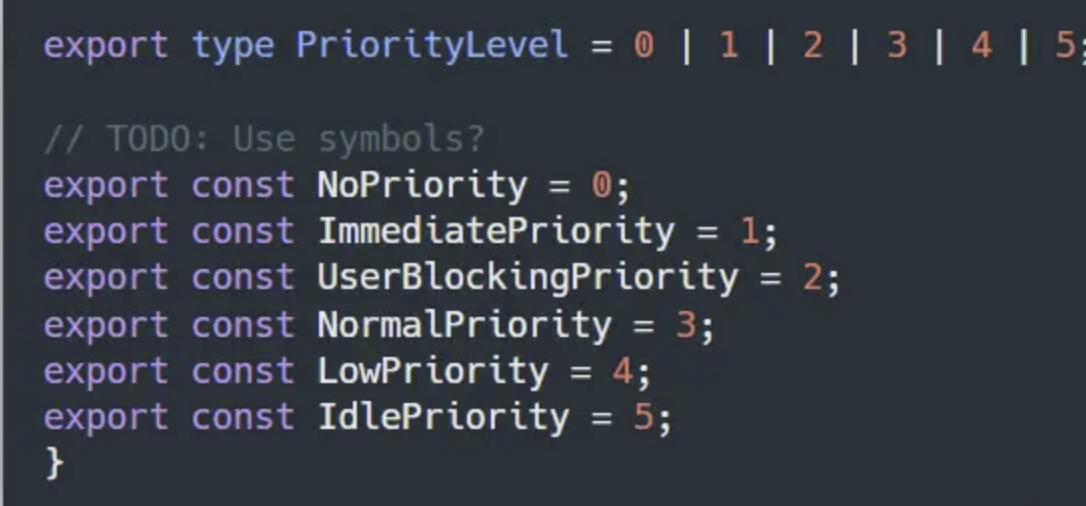
一、39组合总和
本题是集合里元素可以用无数次,那么和组合问题的差别,其实仅在于对startIndex上的控制
题目链接:组合总和
文章讲解:代码随想录
视频讲解:带你学透回溯算法-组合总和 (39.组合总和)
1.思路分析
本题和77.组合,216.组合总和III的区别是:本题没有数量要求,可以无限重复,但是有总和的限制,所以间接的也是有个数的限制。
本题搜索的过程抽象成树形结构如下:

注意图中叶子节点的返回条件,因为本题没有组合数量要求,仅仅是总和的限制,所以递归没有层数的限制,只要选取的元素总和超过target,就返回!
回溯三部曲:
1)递归函数参数
这里依然是定义两个全局变量,二维数组result存放结果集,数组path存放符合条件的结果。(这两个变量可以作为函数参数传入),另外还有各自的栈顶指针ansTop、pathTop。
首先是题目中给出的参数,集合candidates, 和目标值target。
此外我还定义了int型的sum变量来统计单一结果path里的总和,其实这个sum也可以不用,用target做相应的减法就可以了,最后如何target==0就说明找到符合的结果了,但为了代码逻辑清晰,我依然用了sum。
同时,本题还需要startIndex来控制for循环起始位置length记录每个path数组长度。
int* path;
int pathTop;
int** ans;
int ansTop;
//记录每一个和等于target的path数组长度
int* length;
void backTracking(int target, int index, int* candidates, int candidatesSize, int sum)2)递归终止条件
从叶子节点可以清晰看到,终止只有两种情况,sum大于target和sum等于target。
sum等于target的时候,需要收集结果,代码如下:
if(sum >= target) {
//若sum等于target,将当前的组合放入ans数组中
if(sum == target) {
int* tempPath = (int*)malloc(sizeof(int) * pathTop);
int j;
for(j = 0; j < pathTop; j++) {
tempPath[j] = path[j];
}
ans[ansTop] = tempPath;
length[ansTop++] = pathTop;
}
return ;
}3)单层搜索逻辑
单层for循环依然是从startIndex开始,搜索candidates集合,且可重复选取。
int i;
for(i = index; i < candidatesSize; i++) {
//将当前数字大小加入sum
sum+=candidates[i];
path[pathTop++] = candidates[i];
backTracking(target, i, candidates, candidatesSize, sum);
sum-=candidates[i];
pathTop--;
}2.代码详解
/**
* Return an array of arrays of size *returnSize.
* The sizes of the arrays are returned as *returnColumnSizes array.
* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
*/
int* path;
int pathTop;
int** ans;
int ansTop;
//记录每一个和等于target的path数组长度
int* length;
void backTracking(int target, int index, int* candidates, int candidatesSize, int sum) {
//若sum>=target就应该终止遍历
if(sum >= target) {
//若sum等于target,将当前的组合放入ans数组中
if(sum == target) {
int* tempPath = (int*)malloc(sizeof(int) * pathTop);
int j;
for(j = 0; j < pathTop; j++) {
tempPath[j] = path[j];
}
ans[ansTop] = tempPath;
length[ansTop++] = pathTop;
}
return ;
}
int i;
for(i = index; i < candidatesSize; i++) {
//将当前数字大小加入sum
sum+=candidates[i];
path[pathTop++] = candidates[i];
backTracking(target, i, candidates, candidatesSize, sum);
sum-=candidates[i];
pathTop--;
}
}
int** combinationSum(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes){
//初始化变量
path = (int*)malloc(sizeof(int) * 50);
ans = (int**)malloc(sizeof(int*) * 200);
length = (int*)malloc(sizeof(int) * 200);
ansTop = pathTop = 0;
backTracking(target, 0, candidates, candidatesSize, 0);
//设置返回的数组大小
*returnSize = ansTop;
*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
int i;
for(i = 0; i < ansTop; i++) {
(*returnColumnSizes)[i] = length[i];
}
return ans;
}二、40组合总和II
本题开始涉及到一个问题了:去重。
注意题目中给我们 集合是有重复元素的,那么求出来的 组合有可能重复,但题目要求不能有重复组合。
题目链接:组合总和II
文章讲解:代码随想录
视频讲解:回溯算法中的去重,树层去重树枝去重,你弄清楚了没?40.组合总和II
1.思路分析
这道题目和 39组合总和 有如下区别:
本题candidates 中的每个数字在每个组合中只能使用一次。
本题数组candidates的元素是有重复的,而 39组合总和 是无重复元素的数组candidates 最后本题和 39组合总和 要求一样,解集不能包含重复的组合。本题的难点在于:集合(数组candidates)有重复元素,但还不能有重复的组合。
因此这道题我们要在搜索过程中去掉重复组合。
我们都知道组合问题可以抽象为树形结构,那么“使用过”在这个树形结构上是有两个维度的,一个维度是同一树枝上使用过,一个维度是同一树层上使用过。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。
那么问题来了,我们是要同一树层上使用过,还是同一树枝上使用过呢?
回看一下题目,元素在同一个组合内是可以重复的,怎么重复都没事,但两个组合不能相同。
所以我们要去重的是同一树层上的“使用过”,同一树枝上的都是一个组合里的元素,不用去重。
强调一下,树层去重的话,需要对数组排序!
为了理解去重我们来举一个例子,candidates = [1, 1, 2], target = 3,(方便起见candidates已经排序了)

回溯三部曲:
1)递归函数参数
int* path;
int pathTop;
int** ans;
int ansTop;
//记录ans中每一个一维数组的大小
int* length;
void backTracking(int* candidates, int candidatesSize, int target, int sum, int startIndex)2)递归终止条件
if(sum >= target) {
//若sum等于target,复制当前path进入
if(sum == target) {
int* tempPath = (int*)malloc(sizeof(int) * pathTop);
int j;
for(j = 0; j < pathTop; j++) {
tempPath[j] = path[j];
}
length[ansTop] = pathTop;
ans[ansTop++] = tempPath;
}
return ;
}3)单层搜索逻辑
循环过程中,如果遇到与前一个相同的元素就应该跳过,因此运用到了continue。
int i;
for(i = startIndex; i < candidatesSize; i++) {
//对同一层树中使用过的元素跳过
if(i > startIndex && candidates[i] == candidates[i-1])
continue;
path[pathTop++] = candidates[i];
sum += candidates[i];
backTracking(candidates, candidatesSize, target, sum, i + 1);
//回溯
sum -= candidates[i];
pathTop--;
}补充:
在代码中,为了将数组排序,用到了cmp函数以及qsort函数,具体用法如下:
int cmp(const void* a1, const void* a2) {
return *((int*)a1) - *((int*)a2);
}- 它接受两个const void*参数a1和a2,它们分别表示要比较的数组元素的指针。
- 在函数内部,这些指针被强制转换为int*类型,以将它们视为整数指针。
- 使用*对a1和a2指向的实际整数进行解引用,然后进行相减操作。
- 如果减法的结果为负数,则意味着在排序后a1应该位于a2之前。如果是正数,则a1应该位于a2之后。如果结果为零,则它们被视为相等。
- 返回比较的结果。
然后,可以将这个函数与要排序的数组一起传递给qsort函数。qsort使用这个比较函数对数组元素进行升序排序。
//快速排序candidates,让相同元素挨到一起
qsort(candidates, candidatesSize, sizeof(int), cmp);
// qsort(void *base, size_t nmemb, size_t size, int (*compar)(const void *, const void *));
- base:指向要排序的数组的首元素的指针。
- nmemb:数组中元素的个数。
- size:每个元素的大小(以字节为单位)。
- compar:用于比较两个元素的函数指针。
2.代码详解
/**
* Return an array of arrays of size *returnSize.
* The sizes of the arrays are returned as *returnColumnSizes array.
* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
*/
int* path;
int pathTop;
int** ans;
int ansTop;
//记录ans中每一个一维数组的大小
int* length;
int cmp(const void* a1, const void* a2) {
return *((int*)a1) - *((int*)a2);
}
void backTracking(int* candidates, int candidatesSize, int target, int sum, int startIndex) {
if(sum >= target) {
//若sum等于target,复制当前path进入
if(sum == target) {
int* tempPath = (int*)malloc(sizeof(int) * pathTop);
int j;
for(j = 0; j < pathTop; j++) {
tempPath[j] = path[j];
}
length[ansTop] = pathTop;
ans[ansTop++] = tempPath;
}
return ;
}
int i;
for(i = startIndex; i < candidatesSize; i++) {
//对同一层树中使用过的元素跳过
if(i > startIndex && candidates[i] == candidates[i-1])
continue;
path[pathTop++] = candidates[i];
sum += candidates[i];
backTracking(candidates, candidatesSize, target, sum, i + 1);
//回溯
sum -= candidates[i];
pathTop--;
}
}
int** combinationSum2(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes){
path = (int*)malloc(sizeof(int) * 50);
ans = (int**)malloc(sizeof(int*) * 100);
length = (int*)malloc(sizeof(int) * 100);
pathTop = ansTop = 0;
//快速排序candidates,让相同元素挨到一起
qsort(candidates, candidatesSize, sizeof(int), cmp);
backTracking(candidates, candidatesSize, target, 0, 0);
*returnSize = ansTop;
*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
int i;
for(i = 0; i < ansTop; i++) {
(*returnColumnSizes)[i] = length[i];
}
return ans;
}
三、131分割回文串
本题较难,大家先看视频来理解 分割问题,明天还会有一道分割问题,先打打基础。
题目链接:分割回文串
文章讲解:代码随想录
视频讲解:带你学透回溯算法-分割回文串 131.分割回文串
1.思路分析
我们来分析一下切割,其实切割问题类似组合问题。
例如对于字符串abcdef:
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个.....。
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段.....。
感受出来了不?
所以切割问题,也可以抽象为一棵树形结构,如图:

递归用来纵向遍历,for循环用来横向遍历,切割线(就是图中的红线)切割到字符串的结尾位置,说明找到了一个切割方法。
此时可以发现,切割问题的回溯搜索的过程和组合问题的回溯搜索的过程是差不多的。
回溯三部曲:
1)递归函数参数
char** path;
int pathTop;
char*** ans;
int ansTop = 0;
int* ansSize;
void backTracking(char* str, int strLen, int startIndex)2)递归函数终止条件
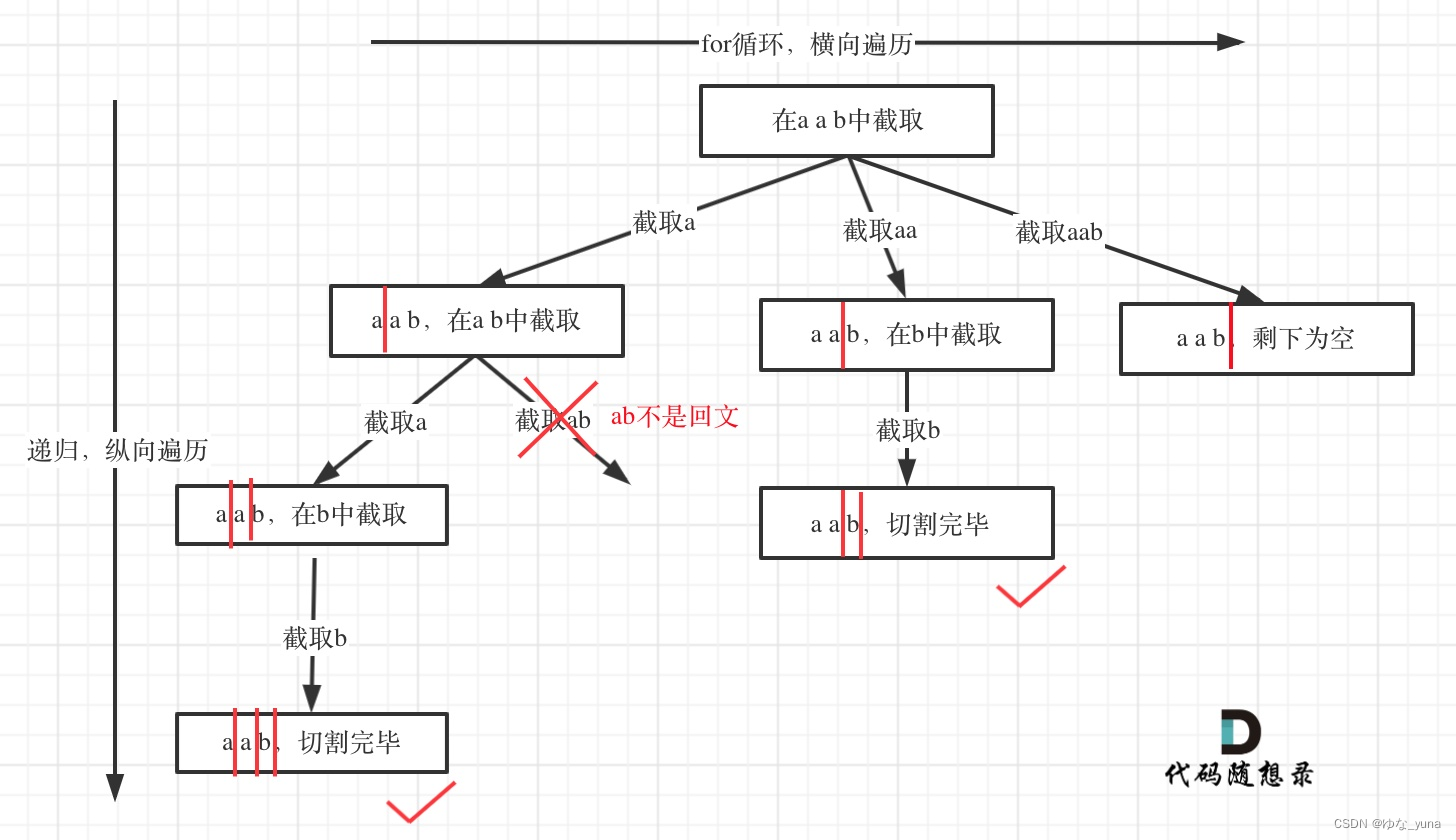
从树形结构的图中可以看出:切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。
那么在代码里什么是切割线呢?
在处理组合问题的时候,递归参数需要传入startIndex,表示下一轮递归遍历的起始位置,这个startIndex就是切割线。
所以终止条件代码如下:
if(startIndex >= strLen) {
//将path拷贝到ans中
copy();
return ;
}3)单层搜索逻辑
在循环中,[startIndex, i] 就是要截取的子串。
首先判断这个子串是不是回文,如果是回文,就将cutString(str, startIndex, i)加入在path[pathTop++]中,path用来记录切割过的回文子串。
int i;
for(i = startIndex; i < strLen; i++) {
//若从subString到i的子串是回文字符串,将其放入path中
if(isPalindrome(str, startIndex, i)) {
path[pathTop++] = cutString(str, startIndex, i);
}
//若从startIndex到i的子串不为回文字符串,跳过这一层
else {
continue;
}
//递归判断下一层
backTracking(str, strLen, i + 1);
//回溯,将path中最后一位元素弹出
pathTop--;
}补充:
1)如何判断回文子串?
最后我们看一下回文子串要如何判断了,判断一个字符串是否是回文。
可以使用双指针法,一个指针从前向后,一个指针从后向前,如果前后指针所指向的元素是相等的,就是回文字符串了。
//判断字符串是否为回文字符串
bool isPalindrome(char* str, int startIndex, int endIndex) {
//双指针法:当endIndex(右指针)的值比startIndex(左指针)大时进行遍历
while(endIndex >= startIndex) {
//若左指针和右指针指向元素不一样,返回False
if(str[endIndex--] != str[startIndex++])
return 0;
}
return 1;
}2)如何切割回文子串?
//切割从startIndex到endIndex子字符串
char* cutString(char* str, int startIndex, int endIndex) {
//开辟字符串的空间
char* tempString = (char*)malloc(sizeof(char) * (endIndex - startIndex + 2));
int i;
int index = 0;
//复制子字符串
for(i = startIndex; i <= endIndex; i++)
tempString[index++] = str[i];
//用'\0'作为字符串结尾
tempString[index] = '\0';
return tempString;
}2.代码详解
/**
* Return an array of arrays of size *returnSize.
* The sizes of the arrays are returned as *returnColumnSizes array.
* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
*/
char** path;
int pathTop;
char*** ans;
int ansTop = 0;
int* ansSize;
//将path中的字符串全部复制到ans中
void copy() {
//创建一个临时tempPath保存path中的字符串
char** tempPath = (char**)malloc(sizeof(char*) * pathTop);
int i;
for(i = 0; i < pathTop; i++) {
tempPath[i] = path[i];
}
//保存tempPath
ans[ansTop] = tempPath;
//将当前path的长度(pathTop)保存在ansSize中
ansSize[ansTop++] = pathTop;
}
//判断字符串是否为回文字符串
bool isPalindrome(char* str, int startIndex, int endIndex) {
//双指针法:当endIndex(右指针)的值比startIndex(左指针)大时进行遍历
while(endIndex >= startIndex) {
//若左指针和右指针指向元素不一样,返回False
if(str[endIndex--] != str[startIndex++])
return 0;
}
return 1;
}
//切割从startIndex到endIndex子字符串
char* cutString(char* str, int startIndex, int endIndex) {
//开辟字符串的空间
char* tempString = (char*)malloc(sizeof(char) * (endIndex - startIndex + 2));
int i;
int index = 0;
//复制子字符串
for(i = startIndex; i <= endIndex; i++)
tempString[index++] = str[i];
//用'\0'作为字符串结尾
tempString[index] = '\0';
return tempString;
}
void backTracking(char* str, int strLen, int startIndex) {
if(startIndex >= strLen) {
//将path拷贝到ans中
copy();
return ;
}
int i;
for(i = startIndex; i < strLen; i++) {
//若从subString到i的子串是回文字符串,将其放入path中
if(isPalindrome(str, startIndex, i)) {
path[pathTop++] = cutString(str, startIndex, i);
}
//若从startIndex到i的子串不为回文字符串,跳过这一层
else {
continue;
}
//递归判断下一层
backTracking(str, strLen, i + 1);
//回溯,将path中最后一位元素弹出
pathTop--;
}
}
char*** partition(char* s, int* returnSize, int** returnColumnSizes){
int strLen = strlen(s);
//因为path中的字符串最多为strLen个(即单个字符的回文字符串),所以开辟strLen个char*空间
path = (char**)malloc(sizeof(char*) * strLen);
//存放path中的数组结果
ans = (char***)malloc(sizeof(char**) * 40000);
//存放ans数组中每一个char**数组的长度
ansSize = (int*)malloc(sizeof(int) * 40000);
ansTop = pathTop = 0;
//回溯函数
backTracking(s, strLen, 0);
//将ansTop设置为ans数组的长度
*returnSize = ansTop;
//设置ans数组中每一个数组的长度
*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
int i;
for(i = 0; i < ansTop; ++i) {
(*returnColumnSizes)[i] = ansSize[i];
}
return ans;
}如果你有问题或者有其他想法,欢迎评论区留言,大家可以一起探讨。