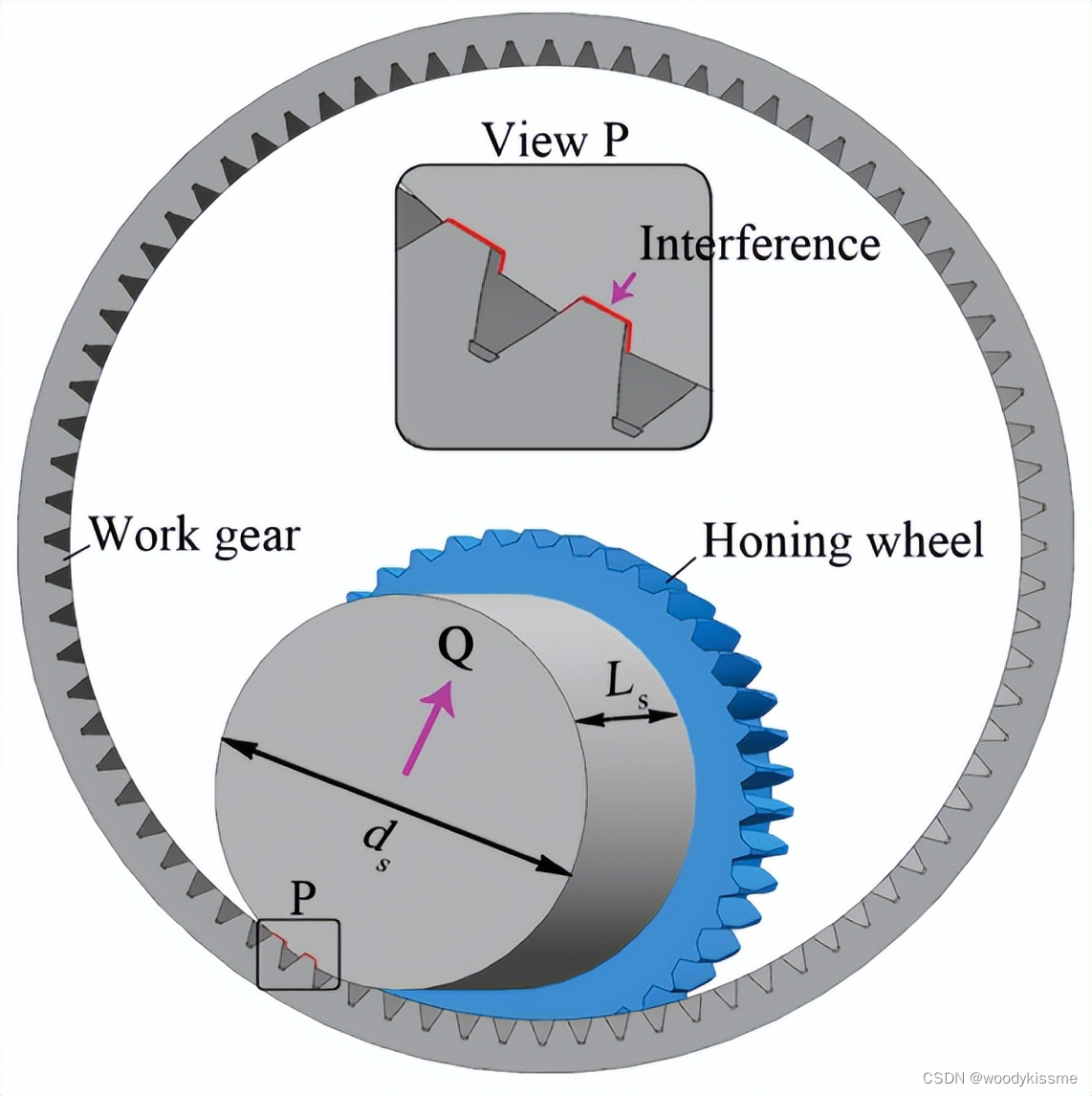
1、原理介绍

        由Edelsbrunner H提出的alpha shapes算法是一种简单、有效的快速提取边界点算法。其克服了点云边界点形状影响的缺点，可快速准确提取边界点。如下图所示，对于任意形状的平面点云，若一个半径为a的圆，绕其进行滚动，其滚动的轨迹形成的点为轮廓点。需要注意的是，alpha shapes算法只能探测二维点的轮廓点。因此在提取点云轮廓点直线，需要将点投影在二维平面上，一般是XOY平面，此时将所有点的z坐标均设置成相同的常数即可，如z=0。

2、测试结果

      基于MATLAB的alpha shapes的边缘点提取，主要包括原始点云可视化、提取边缘点可视化、原始点云与提取边缘点可视化、滚动圆可视化4块部分。

     代码下载链接：https://download.csdn.net/download/qq_32867925/89252183

     在测试数据时，只需要将load中加载数据进行修改即可。使用是，将matlab软件当前路径设置为alphashapedetectbounpts.m文件所在路径。

    部分代码展示：

   使用kdtree搜索近邻点：

[idx,D]=rangesearch(data,data,2*r);%使用kdtree搜索近邻点

判断一个点是否为边缘点：

        for k=1:knn-1%少可一个点 for4
            x3=currentKNN(k,1);
            y3=currentKNN(k,2);
            d1=sqrt((x3-x2)*(x3-x2)+(y3-y2)*(y3-y2));
            d2=sqrt((x3-x21)*(x3-x21)+(y3-y21)*(y3-y21));           
            if (d1>r)
                count=count+1;
            elseif(d2>r)
                count01=count01+1;
            end
        end       
        if (count==knn-1)
             bounpts=[bounpts;data(i,1),data(i,2)];
             circle_XY=[circle_XY;x2,y2];
             break;
        elseif (count01==knn-1)
            bounpts=[bounpts;data(i,1),data(i,2)];  
            circle_XY=[circle_XY;x21,y21];
            break;%终止for3  

2.1无孔洞点云

      如下图为无孔洞点云，alpha shapes提取的边缘点符合真实情况，将边缘点构成的圆进行可视化，可以发现滚动圆均位于外侧，表明该算法提取的边缘点，类似一个滚动圆滚动点云而得到。

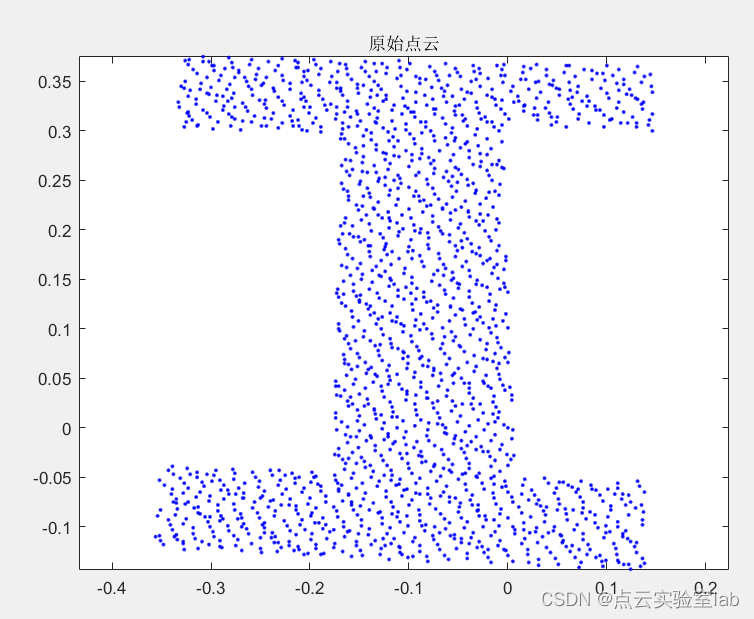原始点云	边缘点提取结果
原始点与边缘点	滚动圆与边缘点

2.2有孔洞点云

      如下图为无孔洞点云，alpha shapes提取的边缘点符合真实情况，将边缘点构成的圆进行可视化，可以发现滚动圆均位于外侧，表明该算法提取的边缘点，类似一个滚动圆滚动点云而得到。同时，位于内部的边缘点，也被准确提取出，效果理想。

原始点云	边缘点提取结果
原始点与边缘点	滚动圆与边缘点

3、总结

      基于alpha shapes提取边缘时，该方法只能提取位于一个平面上的点云数据的边缘，且只与滚动圆半径相关，提取效果一般比较理想。

基于matlab的源码下载链接：https://download.csdn.net/download/qq_32867925/89252183