1.基于蒙特卡罗方法和截断的方法计算（TMC—Shapley）

• 输入
  • 训练数据集D
  • 学习算法A
  • 表现分V
• 输出
  • 各方数据的贡献${\varphi }_i$
• 初始化
  • 初始化各方的贡献${\varphi }_i=0$,并设置当前迭代轮次为0
• 过程
  • 1. 算法进入一个循环迭代，直到满足收敛条件为止
  • 2. 在每次迭代中，算法生成一个随机的训练数据点排列${\pi }^t$
  • 3. 算法初始化一个性能值$v_0^t$,表示空集的性能
  • 4. 对于每个j
  • 4. 1 V(D)代表利用所有训练集训练出来的模型表现
  • 4. 2 如果利用当前随机排列的前j个数据集进行训练后的模型表现与V(D)的值小于预先定义的性能容差（Performance Tolerance），则表示后续数据集的增加不会产生新的边际贡献。
  • 4. 3 否则，则需根据前j个数据集重新训练模型，得到一个新的模型表现
  • 4. 4 更新贡献度，利用前一轮贡献和这一轮的表现更新得到这一轮结束后的贡献

缺点：
上述算法存在一个比较严重的问题，就上每次都要重新训练模型。这在联邦学习场景下几乎是不能被接受的。

2. 基于梯度的Shapley值的计算（G-Shapley）

• 输入
  • 训练数据集 D = { 1 , . . . , n } D=\{1,...,n\} D={1,...,n}
  • 参数化和可微的损失函数$L(.;\theta )$
  • 表现评分函数$V(\theta )$
• 输出
  • 各方数据的贡献${\varphi }_i$
• 初始化
  • 初始化各方的贡献${\varphi }_i=0$,并设置当前迭代轮次为0
• 过程
  • 1. 算法进入一个循环迭代，直到满足收敛条件为止(迭代t+1)
  • 2. 在每次迭代中，算法生成一个随机的训练数据点排列${\pi }^t$
  • 3. 初始化一个随机的模型参数${\theta }_0^t$
  • 4. 根据评分函数评价模型的性能表现$v_0^t$
  • 4. 对于每个j
  • 4. 1 利用随机序列中的前j个数据集训练1epoch来更新模型
  • 4. 2 重新评估模型的性能
  • 4. 3 更新贡献度，利用前一轮贡献和这一轮的表现更新得到这一轮结束后的贡献

缺点：
该算法避免了模型的全部重训练，但只使用一轮的epoch来代表各方的贡献似乎存在一定的问题。

3.实验

• LOO（留一法）
• TMC-Shapley
• G-Shapley
• Random

3.1 实验1

经过我们的设计后，我们可以得到各方数据的贡献度。

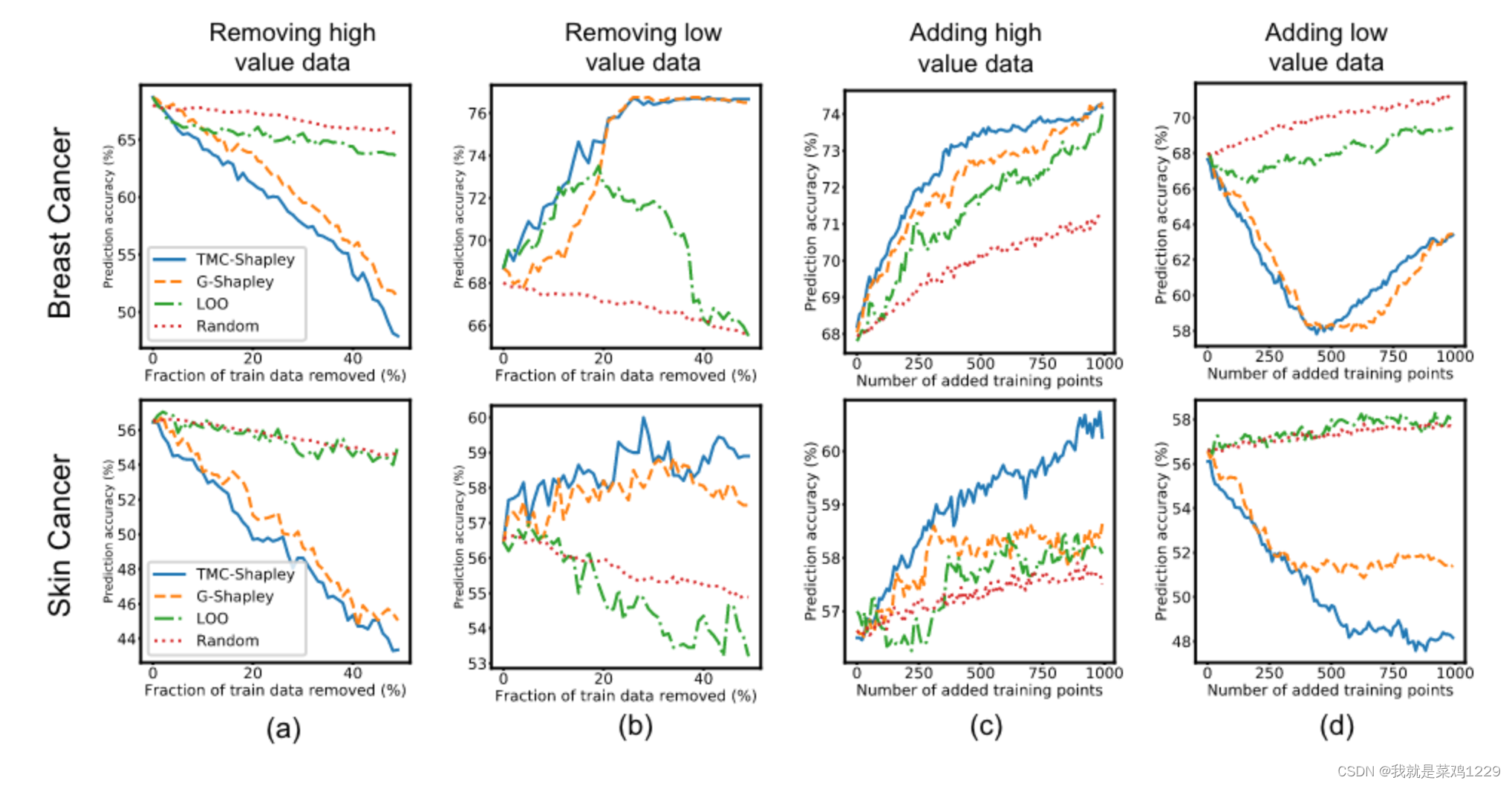
疾病预测 对于乳腺癌和皮肤癌预测任务，我们使用TMC-Shapley、G-Shapley和留一法(LOO)计算训练集中每个点的价值。

• (a) 我们根据三种方法以及均匀抽样的排名，从训练集中删除最有价值的数据。Shapley方法识别了重要的数据点，而删除最有价值的TMC-Shapley或G-Shapley数据点会导致性能比随机删除数据更差。但这对于LOO并不成立。
• (b) 从训练集中删除低TMC-Shapley或G-Shapley值的数据可以改善预测性能。
• © 我们获取了与训练数据中高TMC-Shapley或G-Shapley值患者相似的新患者。与添加随机患者相比，这导致了更大的性能增益。
• (d) 获取与低TMC-Shapley或G-Shapley值患者相似的新患者并不会帮助。

3.2 标签错误

使用众包对数据集进行标记容易出错（Frénay & Verleysen, 2014），并且误标记数据可以被用作简单的数据污染方法（Steinhardt et al., 2017）。在这个实验中，给定一个带有噪声标签的训练数据，我们检查并纠正错误标记的示例，通过检查从最不有价值到最有价值的数据点，因为我们期望错误标记的示例在最不有价值的点中（有些有负的Shapley值）。

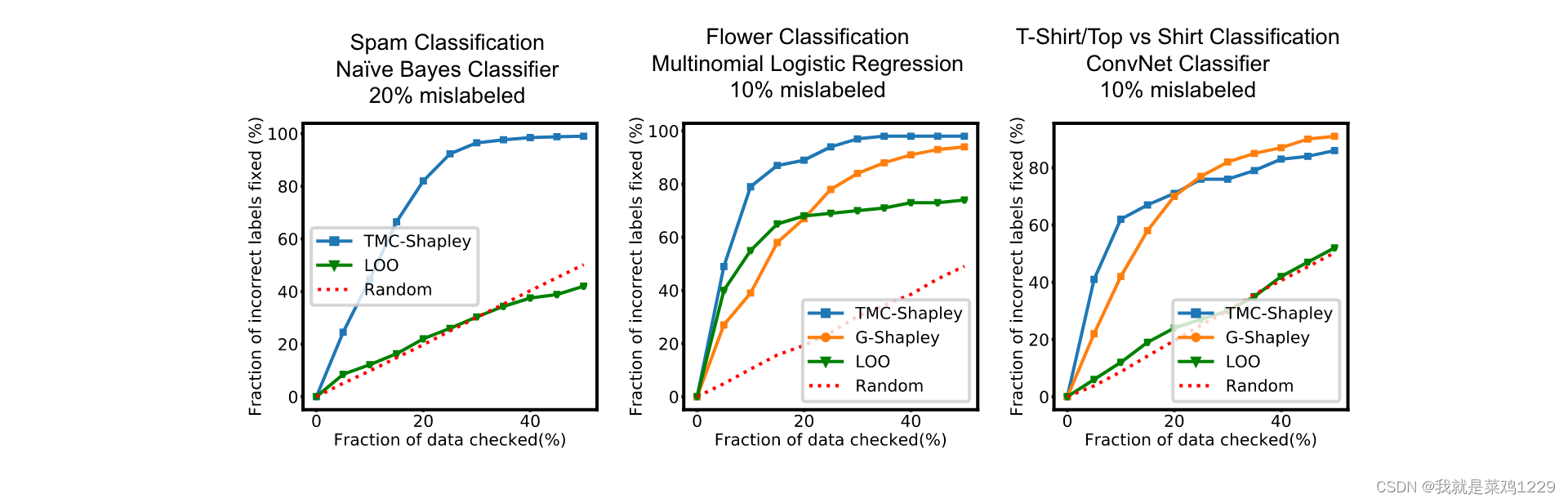
从价值最低的训练数据点到最有价值的数据点检查并修复错误标记的示例。正如所示，Shapley值方法导致最早检测到错误标记的示例。虽然留一法在逻辑回归模型上表现得相当不错，但在另外两个模型上的表现与随机检查相似。

通过检查这些价值低的，我们能够发现更多的标签错误，从而修复，提高模型的准确率。