目录

前言 

引入 

1) Fibonacci

2) 最短路径 - Bellman-Ford

3) 不同路径-Leetcode 62

4) 0-1 背包问题

降维

5) 完全背包问题

降维

6) 零钱兑换问题-Leetcode322

降维

零钱兑换 II-Leetcode 518

7) 钢条切割问题

降维

类似题目 Leetcode-343 整数拆分

8) 最长公共子串

类似题目 Leetcode-718 最长重复子数组

9) 最长公共子序列

最长公共子序列-Leetcode 1143

两个字符串的删除操作-Leetcode 583

10) 最长上升子序列-Leetcode 300

Leetcode-96 不同的二叉搜索树

11) Catalan 数

Leetcode-22 括号生成

买票找零问题

12) 打家劫舍-Leetcode 198

13) Travelling salesman problem

---

前言 

The quote “Those who forget history are condemned to repeat it” is attributed to the American philosopher George Santayana and it can be accurately quoted as “Those who cannot remember the past are condemned to repeat it” as stated in his work, The Life of Reason: Reason in Common Sense.

 “那些忘记历史的人注定重蹈覆辙”这句话出自美国哲学家乔治·桑塔亚那之手，准确地说，这句话可以被引用为他在《理性的生活:常识中的理性》一书中所说的“那些不记得过去的人注定重蹈覆辙”。  “Those who cannot remember the past are condemned to repeat it”  这句话忘记是在哪里看到的了,但是我觉得用在动态规划这个章节,真的很合适!

引入 

 我们可以先来看一个简单的例子,我们之前用递归的方法来求解斐波那契的第n项

1) Fibonacci

public class Fibonacci {

    public static int fibonacci(int n){
        if(n==0){
            return 0;
        }
        if(n==1){
            return 1;
        }
        int x = fibonacci(n-1);
        int y = fibonacci(n-2);
        return x+y;
    }
}

但是这个代码有缺点:

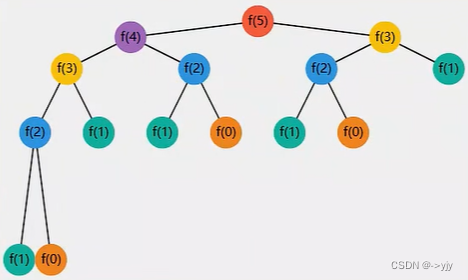
重复计算了非常多的数据.

后来我们想要用记忆法来优化: 

/**
     * <h3>使用 Memoization(记忆法, 也称备忘录) 改进</h3>
     *
     * @param n 第 n 项
     * @return 第 n 项的值
     */
    public static int fibonacci(int n) {
        int[] cache = new int[n + 1];
        Arrays.fill(cache, -1); // [-1,-1,-1,-1,-1,-1]
        cache[0] = 0;
        cache[1] = 1; // [0,1,-1,-1,-1,-1]
        return f(n, cache);
    }

    // f(3) => 5
    // f(4) => 9
    // f(5) => 15
    //         2*f(n+1) - 1
    private static int f(int n, int[] cache) {
        /*if (n == 0) {
            return 0;
        }
        if (n == 1) {
            return 1;
        }*/
        if (cache[n] != -1) {
            return cache[n];
        }

        int x = f(n - 1, cache);
        int y = f(n - 2, cache);
        cache[n] = x + y; // // [0,1,?,-1,-1,-1] 存入数组
        return cache[n];
    }

动态规划也是对递归过程进行改进,只是它是从另外一种方向进行改进,避免重复计算

/**
 * 求斐波那契数列的第n项（动态规划）
 */
public class Fibonacci {
    public static void main(String[] args) {
        System.out.println(fibonacci2(13));
    }
    /*
        要点1：
            从已知子问题的解，推导出当前问题的解
            推导过程可以表达为一个数学公式
        要点2：
            用一维或二维数组来保存之前的计算结果（可以进一步优化）

        Dynamic-Programming - 由 Bellman 提出
        动态     编程
            Programming - 在这里指用数学方法来根据子问题求解当前问题（通俗理解就是找到递推公式）
            Dynamic     - 指缓存上一步结果，根据上一步结果计算当前结果（多阶段进行）

        合在一起：
            找出递归公式，将当前问题分解成子问题，分阶段进行求解。
            求解过程中缓存子问题的解，避免重复计算。
     */
    public static int fibonacci2(int n) {
        if (n == 0) {
            return 0;
        }
        if (n == 1) {
            return 1;
        }
        int a = 0;
        int b = 1;
        for (int i = 2; i <= n ; i++) {
            int c = b + a;
            a = b;
            b = c;
        }
        return b;
    }

    public static int fibonacci(int n) {
        int[] dp = new int[n + 1]; // 用来缓存结果
        if (n == 0) {
            dp[0] = 0;
            return 0;
        }
        if (n == 1) {
            dp[1] = 1;
            return 1;
        }
        for (int i = 2; i <= n ; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

2) 最短路径 - Bellman-Ford

假设要求v1-->v4的最短距离是多少?

分析:

 /*
            f(v) 用来表示从起点出发，到达 v 这个顶点的最短距离
            初始时
            f(v) = 0   当 v==起点 时
            f(v) = ∞   当 v!=起点 时

            之后
            新           旧     所有from
            f(to) = min(f(to), f(from) + from.weight)

            from 从哪来
            to   到哪去

            f(v4) = min( ∞, f(v3) + 11 ) = 20
            f(v4) = min( 20, f(v2) + 15 ) = 20

            v1  v2  v3  v4  v5  v6
            0   ∞   ∞   ∞   ∞   ∞
            0   7   9   ∞   ∞   14  第一轮
            0   7   9   20  23  11  第二轮
            0   7   9   20  20  11  第三轮
            0   7   9   20  20  11  第四轮
            0   7   9   20  20  11  第五轮

     */
 

public class BellmanFord {
    static class Edge {
        int from;
        int to;
        int weight;

        public Edge(int from, int to, int weight) {
            this.from = from;
            this.to = to;
            this.weight = weight;
        }
    }

   
    public static void main(String[] args) {
        List<Edge> edges = List.of(
                new Edge(6, 5, 9),
                new Edge(4, 5, 6),
                new Edge(1, 6, 14),
                new Edge(3, 6, 2),
                new Edge(3, 4, 11),
                new Edge(2, 4, 15),
                new Edge(1, 3, 9),
                new Edge(1, 2, 7)
        );
        int[] dp = new int[7]; // 一维数组用来缓存结果
        dp[1] = 0;
        for (int i = 2; i < dp.length; i++) {
            dp[i] = Integer.MAX_VALUE;
        }
        print(dp);
        for (int i = 0; i < 5; i++) {
            for (Edge e : edges) {//更新到达v4顶点的最短路径
                if(dp[e.from] != Integer.MAX_VALUE) {
                    dp[e.to] = Integer.min(dp[e.to], dp[e.from] + e.weight);
                }
            }
        }
        print(dp);
    }

    static void print(int[] dp) {
        System.out.println(Arrays.stream(dp)
                .mapToObj(i -> i == Integer.MAX_VALUE ? "∞" : String.valueOf(i))
                .collect(Collectors.joining(",", "[", "]")));
    }
}

3) 不同路径-Leetcode 62

机器人要从左上角走到右下角，每次只能向右或向下，问一共有多少条不同路径？

分析，先考虑较为简单的情况

可能路径有三种情况：

• 👉 👇 👇

• 👇 👇👉

• 👇👉👇

分析：设坐标为，共有 m 行 n 列

(0,0)   (0,1)
(1,0)   (1,1)
(2,0)   (2,1)

如果终点是 (0,1) 那么只有一种走法

如果终点是 (1,0) 那么也只有一种走法

如果终点是 (1,1) 呢，它的走法是从它的上方走下来，或者从它的左边走过来，因此走法 = (0,1) + (1,0) = 2种

如果终点是 (2,0) 那么也只有一种走法

如果终点是 (2,1) 呢，它的走法是从它的上方走下来，或者从它的左边走过来，因此走法 = (1,1) + (2,0) = 3种

总结规律发现：

1. 终点是 (0,1) (0,2) (0,3) ... (0,n) 走法只有1种

2. 终点是 (1,0) (2,0) (3,0) ... (m,0) 走法也只有1种

3. 除了上面两种情况以外，(i,j) 处的走法等于(i-1,j) + (i,j-1) 的走法之和，即为递推公式

画表格

0   1   1   1   1   1   1
1   2   3   4   5   6   7
1   3   6   10  15  21  28

import java.util.Arrays;
import java.util.stream.IntStream;

public class UniquePaths {
    public static void main(String[] args) {
        int count = new UniquePaths().uniquePaths(3, 7);
        System.out.println(count);
    }

    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int j = 0; j < n; j++) {
            dp[0][j] = 1;
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        print(dp);
        return dp[m - 1][n - 1];
    }
    static void print(int[][] dp){
        System.out.println("-".repeat(20));
        Object[] array = IntStream.range(0,dp[0].length+1).boxed().toArray();
        System.out.printf(("%2d ".repeat(dp[0].length))+"%n",array);
        for(int[] d:dp){
            array = Arrays.stream(d).boxed().toArray();
            System.out.printf(("%2d ".repeat(d.length))+"%n",array);
        }
    }
}

降维

public class UniquePaths {
    public static void main(String[] args) {
        int count = new UniquePaths().uniquePaths(3, 7);
        System.out.println(count);
    }

    public int uniquePaths(int m, int n) {
        int[] dp = new int[n];
      //  for(int j =0;j<n;j++){
      //      dp[j]=1;
      //  }
        Arrays.fill(dp, 1);//初始化操作
        for (int i = 1; i < m; i++) {
            dp[0] = 1;//第一列一直不动
            for (int j = 1; j < n; j++) {
                dp[j] = dp[j] + dp[j - 1];
            }
        }
        return dp[n - 1];
    }
}

类似于不规则的杨辉三角

4) 0-1 背包问题

贪心章节所解决不出的问题 贪心算法-活动选择问题&背包问题-CSDN博客

分析: 

/*
        1. n个物品都是固体，有重量和价值
        2. 现在你要取走不超过 10克 的物品
        3. 每次可以不拿或全拿，问最高价值是多少

            编号 重量(g)  价值(元)                        简称
            1   4       1600           黄金一块   400    A
            2   8       2400           红宝石一粒 300    R
            3   5       30             白银一块         S
            0   1       1_000_000      钻石一粒          D
        1_001_630  贪心解

        1_002_400  正确解
     */

    /*行:物品
      列:容量
        1   2   3   4   5   6   7   8   9   10
   0    0   0   0   A   A   A   A   A   A   A    黄金
   1    0   0   0   A   A   A   A   R   R   R    红宝石
   2    0   0   0   A   A   A   A   R   R   R    白银
   3    0   D   D   D  DA   DA  DA  DA  DR  DR   钻石 
   
   -->递推式 
   if(装不下){
           dp[i][j]=dp[i-1][j];
   }else{装得下
           dp[1][8]=max(dp[0][8],R);(不完整)
           dp[3][5]=max(dp[2][5],D + dp[2][5-D.weight]);
           dp[i][j]=max(dp[i-1][j],item.value+dp[i-1][j-item.weight]);
   }
     */

public class KnapsackProblem {
  

    static class Item {
        int index;
        String name;
        int weight;
        int value;

        public Item(int index, String name, int weight, int value) {
            this.index = index;
            this.name = name;
            this.weight = weight;
            this.value = value;
        }

        @Override
        public String toString() {
            return "Item(" + name + ")";
        }
    }

    public static void main(String[] args) {
        Item[] items = new Item[]{
                new Item(1, "黄金", 4, 1600),
                new Item(2, "宝石", 8, 2400),
                new Item(3, "白银", 5, 30),
                new Item(4, "钻石", 1, 10_000),
        };
        System.out.println(select(items, 10));
    }

    static int select(Item[] items, int total) {
        int[][] dp = new int[items.length][total + 1];
        print(dp);
        Item item0 = items[0]; //黄金
        for (int j = 0; j < total + 1; j++) {
            if (j >= item0.weight) {
                dp[0][j] = item0.value;//装得下
            }else{
                dp[0][j]=0;//装不下
            }
        }
        print(dp);
        for (int i = 1; i < dp.length; i++) {
            Item item = items[i];
            for (int j = 1; j < total + 1; j++) {
                // x: 上一次同容量背包的最大价值
                int x = dp[i - 1][j];
                if (j >= item.weight) {
                    // j-item.weight: 当前背包容量-这次物品重量=剩余背包空间
                    // y: 剩余背包空间能装下的最大价值 + 这次物品价值
                    int y = dp[i - 1][j - item.weight] + item.value;
                    dp[i][j] = Integer.max(x, y);
                } else {
                    dp[i][j] = x;
                }
            }
            print(dp);
        }
        return dp[dp.length - 1][total];
    }

    static void print(int[][] dp) {
        System.out.println("   " + "-".repeat(63));
        Object[] array = IntStream.range(0, dp[0].length + 1).boxed().toArray();
        System.out.printf(("%5d ".repeat(dp[0].length)) + "%n", array);
        for (int[] d : dp) {
            array = Arrays.stream(d).boxed().toArray();
            System.out.printf(("%5d ".repeat(d.length)) + "%n", array);
        }
    }
}

降维

static int select(Item[] items, int total) {
    int[] dp = new int[total + 1];
    for (Item item : items) {
        for (int j = total; j > 0; j--) {
            if (j >= item.weight) { // 装得下
                dp[j] = Integer.max(dp[j], item.value + dp[j - item.weight]);
            }
        }
        System.out.println(Arrays.toString(dp));
    }
    return dp[total];
}

注意：内层循环需要倒序，否则 dp[j - item.weight] 的结果会被提前覆盖

5) 完全背包问题

区别:每件物品有无限多 问 将来用这个背包能够装的最大价值

分析:

 /*
            0   1   2   3   4   5   6
        1   0   0   c   c   cc  cc  ccc
        2   0   0   c   s   cc  cs  ccc
        3   0   0   c   s   a   a   ac
        
        if(放得下){
            dp[i][j]=max(dp[i-1][j],dp[i][j-item.weight]+item.value);
        }else{
            dp[i][j]=dp[i-1][j];
        }
     */

public class KnapsackProblemComplete {
    static class Item {
        int index;
        String name;
        int weight;
        int value;

        public Item(int index, String name, int weight, int value) {
            this.index = index;
            this.name = name;
            this.weight = weight;
            this.value = value;
        }

        @Override
        public String toString() {
            return "Item(" + name + ")";
        }
    }

    public static void main(String[] args) {
        Item[] items = new Item[]{
                new Item(1, "青铜", 2, 3),    // c
                new Item(2, "白银", 3, 4),    // s
                new Item(3, "黄金", 4, 7),    // a
        };
        System.out.println(select(items, 6));
    }

   

    private static int select(Item[] items, int total) {
        int[][] dp = new int[items.length][total + 1];
        Item item0 = items[0];
        for (int j = 0; j < total + 1; j++) {
            if (j >= item0.weight) {
                dp[0][j] = dp[0][j - item0.weight] + item0.value;
            }
        }
        print(dp);
        for (int i = 1; i < items.length; i++) {
            Item item = items[i];            
            for (int j = 1; j < total + 1; j++) {
                // x: 上一次同容量背包的最大价值
            	int x = dp[i - 1][j];
                if (j >= item.weight) {
                    // j-item.weight: 当前背包容量-这次物品重量=剩余背包空间
                    // y: 剩余背包空间能装下的最大价值 + 这次物品价值
                    int y = dp[i][j - item.weight] + item.value;
                    dp[i][j] = Integer.max(x, y);
                } else {
                    dp[i][j] = x;
                }
            }
            print(dp);
        }
        return dp[dp.length - 1][total];
    }

    static void print(int[][] dp) {
        System.out.println("   " + "-".repeat(63));
        Object[] array = IntStream.range(0, dp[0].length + 1).boxed().toArray();
        System.out.printf(("%5d ".repeat(dp[0].length)) + "%n", array);
        for (int[] d : dp) {
            array = Arrays.stream(d).boxed().toArray();
            System.out.printf(("%5d ".repeat(d.length)) + "%n", array);
        }
    }
}

降维

private static int select(Item[] items, int total) {
    int[] dp = new int[total + 1];
    for (Item item : items) {
        for (int j = 0; j < total + 1; j++) {
            if (j >= item.weight) {
                dp[j] = Integer.max(dp[j], dp[j - item.weight] + item.value);
            }
        }
        System.out.println(Arrays.toString(dp));
    }
    return dp[total];
}

 

完全背包-->有无数种产品 所以在同一行找

0-1背包-->只有一种产品所以必须在上一行找,否则就会导致选择多个产品 

6) 零钱兑换问题-Leetcode322

凑成总金额的凑法中,需要硬币最少个数是几?

/*
              面值    0     1     2    3     4        5
                  1     0      1   11  111  1111  11111
                  2    0        1    2   12  22     221
                  5    0        1     2   12     22      5
        
        总金额: 类比成背包容量
        硬币面值:类比成物品重量
        硬币个数:类比为物品价值,固定为1(求价值(个数)最小的)
        
        if(装得下){
        min(上次价值(个数),剩余容量能装下的最小价值(个数)+1)
        dp[i][j] = min(dp[i-1][j],dp[i][j-item.weight]+1)
        }else{
        保留上次价值不变  
        dp[i][j] = dp[i-1][j]
        }
        
        特殊情况:
        面值    0     1     2     3     4     5 
        10      max max max max max max
        
    */

public class ChangeMakingProblemLeetcode322 {
    
    public int coinChange(int[] coins, int amount) {
        int max = amount + 1;
        int[][] dp = new int[coins.length][amount + 1];
        for (int j = 1; j < amount + 1; j++) {
            if (j >= coins[0]) {
                dp[0][j] = 1 + dp[0][j - coins[0]];
            } else {
                dp[0][j] = max;
            }
        }

        for (int i = 1; i < coins.length; i++) {
            for (int j = 1; j < amount + 1; j++) {
                if (j >= coins[i]) {
                    dp[i][j] = Math.min(dp[i - 1][j], 1 + dp[i][j - coins[i]]);
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
            print(dp);
        }
        int r = dp[coins.length - 1][amount];
        return r > amount ? -1 : r;
    }

    public static void main(String[] args) {
        ChangeMakingProblemLeetcode322 leetcode = new ChangeMakingProblemLeetcode322();
        int count = leetcode.coinChange(new int[]{1, 2, 5}, 5);
//        int count = leetcode.coinChange(new int[]{25, 10, 5, 1}, 41);
//        int count = leetcode.coinChange(new int[]{2}, 3);
//        int count = leetcode.coinChange(new int[]{15, 10, 1}, 21);
        System.out.println(count);
    }

    static void print(int[][] dp) {
        System.out.println("-".repeat(18));
        Object[] array = IntStream.range(0, dp[0].length + 1).boxed().toArray();
        System.out.printf(("%2d ".repeat(dp[0].length)) + "%n", array);
        for (int[] d : dp) {
            array = Arrays.stream(d).boxed().toArray();
            System.out.printf(("%2d ".repeat(d.length)) + "%n", array);
        }
    }
}

降维

class Solution {
    public int coinChange(int[] coins, int amount) {
        //完全背包
        int[] dp = new int[amount+1];
        
        for(int j = 1;j<amount+1;j++){
            if(j>=coins[0]){
                dp[j] = dp[j- coins[0]]+1;
            }else{
                dp[j] = amount+1;//最大值
            }
        }
        for(int i = 1;i<coins.length;i++){
            for(int j = 1;j<amount+1;j++){
                if(j>=coins[i]){
                    dp[j] = Math.min(dp[j],dp[j-coins[i]]+1);
                }
            }
        }
        return dp[amount] < amount+1? dp[amount]:-1;
        
    }
}

public int coinChange(int[] coins, int amount) {
    int[] dp = new int[amount + 1];
    Arrays.fill(dp, amount + 1);
    dp[0] = 0;
    // 0 max max max max max
    //
    System.out.println(Arrays.toString(dp));
    for (int coin : coins) {
        for (int j = coin; j < amount + 1; j++) {
            dp[j] = Math.min(dp[j], 1 + dp[j - coin]);
        }
        System.out.println(Arrays.toString(dp));
    }
    int r = dp[amount];
    return r > amount ? -1 : r;
}

零钱兑换 II-Leetcode 518

凑成总金额有几种凑法?

/*

     面值  0        1        2        3        4        5

        1              1        11      111   1111    11111

        2               1        11      111      1111    11111

                                    2         21        211    2111

                                                           22    221

        

        

      5               1        11      111      1111    11111

                                    2         21        211    2111

                                                           22    221

                                                                     5

     面值    0        1        2        3        4        5
       1       1        1        1        1        1        1
       2      1        1        2        2        3        3
       5      1        1        2        2        3        4

     面值    0        1        2        3
       1        1        1       1         1
       2        1        1        2        2

        if(放得下){
            dp[i][j]=dp[i-1][j]+dp[i][j-coin]
        }else(放不下){
            dp[i][j]=dp[i-1][j];
        }
     */
 

class Solution {
    public int change(int amount, int[] coins) {
        int[][] dp = new int[coins.length][amount+1];
        for(int i = 0;i<coins.length;i++){
            dp[i][0] = 1;
        }

        for(int i = 1;i<amount+1;i++){
            if(i>=coins[0]){
                dp[0][i] = dp[0][i-coins[0]];
            }
        }


        for(int i = 1;i<coins.length;i++){
            for(int j = 1;j<amount+1;j++){
                if(j>=coins[i]){
                    dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]];
                }else{
                    dp[i][j] = dp[i-1][j];
                }
            }
        }

        return dp[coins.length-1][amount];
    }
}

public class ChangeMakingProblemLeetcode518 {
    
    public int change(int[] coins, int amount) {
        int[] dp = new int[amount + 1];
        dp[0] = 1;
        for (int coin : coins) {
            for (int j = coin; j < amount + 1; j++) {
                dp[j] = dp[j] + dp[j - coin];
            }
        }
        return dp[amount];
    }

    public static void main(String[] args) {
        ChangeMakingProblemLeetcode518 leetcode = new ChangeMakingProblemLeetcode518();
        int count = leetcode.change(new int[]{1, 2, 5}, 5);
        System.out.println(count);
    }

}

7) 钢条切割问题

怎么切才能得到最大价值?  (完全背包)

 /*
     0	1	2	3	4	5	6	7	8	9	10 (长度为几的钢条)
    0	1	5	8	9	10	17	17	20	24	30 (对应的价值)
    if(放得下)
    	dp[i][j]=max(dp[i-1][j],当前物品的价值+剩余空间的物品价值dp[i][j-物品重量])
    else(放不下)
    	dp[i][j]=dp[i-1][j]
    
    1 5 8 9
            0   1   2   3   4
        1       1   11  111 1111
                (1) (2) (3) (4)
        2           11  111 1111
                    2   21  211
                            22
                (1) (5) (6) (10)
        3       1   11  111 1111
                    2   21  211
                        3   22
                            31
                (1) (5) (8) (10)
        4       1   11  111 1111
                    2   21  211
                        3   22
                            31
                            4
                (1) (5) (8) (10)
     */

public class CutRodProblem {
    
   
    static int cut(int[] values, int n) {
        int[][] dp = new int[values.length][n + 1];
        for (int i = 1; i < values.length; i++) {
            int v = values[i];
            for (int j = 1; j < n + 1; j++) {
                if (j >= i) {
                    dp[i][j] = Integer.max(dp[i - 1][j], v + dp[i][j - i]);
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
            print(dp);
        }
        return dp[values.length - 1][n];
    }

    public static void main(String[] args) {
        //不同长度钢条的价值数组,数组的索引对应钢条的长度(物品重量)
        System.out.println(cut(new int[]{0, 1, 5, 8, 9}, 4));
    }
}

降维

static int cut(int[] values, int n) {
    int[] dp = new int[n + 1];
    for (int i = 1; i < values.length; i++) {
        int v = values[i];
        for (int j = i; j < n + 1; j++) {
            dp[j] = Integer.max(dp[j], v + dp[j - i]);
        }
        System.out.println(Arrays.toString(dp));
    }
    return dp[n];
}

本质上是完全背包问题，把钢条总长度看作背包容量，切分后的钢条看作物品。只是

• 此时的背包容量=物品数量，例如，钢条总长度为4，可以看作有四种物品：

  • 长度1的钢条

  • 长度2的钢条

  • 长度3的钢条

  • 长度4的钢条

• 另外，这个场景下，总能装满背包

类似题目 Leetcode-343 整数拆分

/*
         0   1   2   3   4
     1   1   1   11  111 1111
     2   1   1   11  111 1111
                 2   21  211
                         22
             (1) (2) (2) (4)
     3   1   1   11  111 1111
                 2   21  211
                     3   22
                         31
             (1) (2) (3) (4)
     4   1   1   11  111 1111
                 2   21  211
                     3   22
                         31
                         4
             (1) (2) (3) (4)
     */

public class Leetcode343 {

    public int integerBreak(int n) {
        int[] dp = new int[n + 1];
        Arrays.fill(dp, 1);
        dp[0] = 1;
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < n + 1; j++) {
                if (j >= i) {
                    dp[j] = Integer.max(dp[j], i * dp[j - i]);
                }
            }
            System.out.println(Arrays.toString(dp));
        }
        return dp[n];
    }

    public int integerBreak2(int n) {
        int[][] dp = new int[n][n + 1];
        Arrays.fill(dp[0], 1);
        for (int i = 1; i < n; i++) {
            dp[i][0] = 1;
        }
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < n + 1; j++) {
                if (j >= i) {
                    dp[i][j] = Integer.max(dp[i - 1][j], i * dp[i][j - i]);
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
            print(dp);
        }
        return dp[n - 1][n];
    }

    public static void main(String[] args) {
        Leetcode343 code = new Leetcode343();
        System.out.println(code.integerBreak(4));
        System.out.println(code.integerBreak(10));
    }
}

8) 最长公共子串

/*
            i   t   h   e   i   m   a
         t  0   1   0   0   0   0   0
         h  0   0   2   0   0   0   0
         e  0   0   0   3   0   0   0
         n  0   0   0   0   0   0   0
     */
/*
    if(相同字符){
        dp[i][j] = dp[i-1][j-1] + 1;
    
    }else{
        dp[i][j] = 0;
    }
*/

public class LCSubstring {

    static int lcs(String a, String b) {
        int[][] dp = new int[b.length()][a.length()];
        int max = 0;
        for (int i = 0; i < b.length(); i++) {
            for (int j = 0; j < a.length(); j++) {
                if (a.charAt(j) == b.charAt(i)) {
                    if (i == 0 || j == 0) {
                        dp[i][j] = 1;
                    } else {
                        dp[i][j] = dp[i - 1][j - 1] + 1;
                    }
                    max = Integer.max(dp[i][j], max);
                } else {
                    dp[i][j] = 0;
                }
            }
        }
        print(dp, a, b);
        return max;
    }

    static void print(int[][] dp, String a, String b) {
        System.out.println("-".repeat(23));
        Object[] array = a.chars().mapToObj(i -> String.valueOf((char) i)).toArray();
        System.out.printf("  "+"%2s ".repeat(a.length()) + "%n", array);
        for (int i = 0; i < b.length(); i++) {
            int[] d = dp[i];
            array = Arrays.stream(d).boxed().toArray();
            System.out.printf(b.charAt(i) + " " + "%2d ".repeat(d.length) + "%n", array);
        }
    }
    

    public static void main(String[] args) {
        System.out.println(lcs("itheima", "then"));
    }
}

类似题目 Leetcode-718 最长重复子数组

public class Leetcode718 {

    public int findLength(int[] nums1, int[] nums2) {
        int m = nums1.length + 1;
        int n = nums2.length + 1;
        int[] dp = new int[n];
        int max = 0;
        for (int i = 1; i < m; i++) {
            for (int j = n - 1; j > 0; j--) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[j] = dp[j - 1] + 1;
                    max = Integer.max(max, dp[j]);
                } else {
                    dp[j] = 0;
                }
            }
        }
        return max;
    }

    public int findLength1(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;
        int[] dp = new int[n];
        int max = 0;
        for (int i = 0; i < m; i++) {
            for (int j = n - 1; j >= 0; j--) {
                if (nums1[i] == nums2[j]) {
                    if (i == 0 || j == 0) {
                        dp[j] = 1;
                    } else {
                        dp[j] = dp[j - 1] + 1;
                    }
                    max = Integer.max(max, dp[j]);
                } else {
                    dp[j] = 0;
                }
            }
        }
        return max;
    }

    public int findLength2(int[] nums1, int[] nums2) {
        int[][] dp = new int[nums1.length][nums2.length];
        int max = 0;
        for (int i = 0; i < nums1.length; i++) {
            for (int j = 0; j < nums2.length; j++) {
                if (nums1[i] == nums2[j]) {
                    if (i == 0 || j == 0) {
                        dp[i][j] = 1;
                    } else {
                        dp[i][j] = dp[i - 1][j - 1] + 1;
                    }
                    max = Integer.max(max, dp[i][j]);
                } else {
                    dp[i][j] = 0;
                }
            }
        }
        return max;
    }

    public static void main(String[] args) {
        Leetcode718 code = new Leetcode718();
        System.out.println(code.findLength(new int[]{1, 2, 3, 2, 1}, new int[]{3, 2, 1, 4, 7}));
        System.out.println(code.findLength(new int[]{1, 0, 0, 0, 1}, new int[]{1, 0, 0, 1, 1}));
    }
}

9) 最长公共子序列

最长公共子序列-Leetcode 1143

  /*
         a   b   c   x   y   z
      0  0   0   0   0   0   0
    a 0  1   1   1   1   1   1
    b 0  1   2   2  2    2   2
    c 0  1   2   3  3   3    3
    x 0  1   2   3  4  4     4
    y 0  1   2   3  4   5    6
    z 0  1   2   3  4   5    6

    相同字符
        找到上一行上一列数值+1
    不同字符
        max(上一行,上一列)
     */

public class LCSubsequence {
    public int longestCommonSubsequence(String text1, String text2) {
        int m = text1.length();
        int n = text2.length();
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i < m + 1; i++) {
            char a = text1.charAt(i - 1);
            for (int j = 1; j < n + 1; j++) {
                char b = text2.charAt(j - 1);
                if (a == b) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Integer.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        print(dp, text2, text1);
        return dp[m][n];
    }

    static void print(int[][] dp, String a, String b) {
        System.out.println("-".repeat(23));
        Object[] array = a.chars().mapToObj(i -> String.valueOf((char) i)).toArray();
        System.out.printf("     " + "%2s ".repeat(a.length()) + "%n", array);
        for (int i = 0; i < b.length(); i++) {
            int[] d = dp[i + 1];
            array = Arrays.stream(d).boxed().toArray();
            System.out.printf(b.charAt(i) + " " + "%2d ".repeat(d.length) + "%n", array);
        }
    }

    public static void main(String[] args) {
        LCSubsequence code = new LCSubsequence();
        System.out.println(code.longestCommonSubsequence("abcde", "ace"));
        System.out.println(code.longestCommonSubsequence("ba", "yby"));
    }
}

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int m = text1.length();
        int n = text2.length();
        int[] dp = new int[n+1];
        for(int i = 1;i<m+1;i++){
            char a = text1.charAt(i-1);
            int prev = 0;//存储上一行的dp[j-1],初始化为0
            for(int j = 1;j<n+1;j++){
                char b = text2.charAt(j-1);
                int temp = dp[j];//存储当前dp[j],用于更新下一个dp[j]
                if(a==b){
                    dp[j] = prev+1;
                }else{
                    dp[j] = Math.max(dp[j],dp[j-1]);
                }
                prev = temp;

            }
        }
        return dp[n];
    
    }
}

两个字符串的删除操作-Leetcode 583

public class Leetcode538 {
   public static void main(String[] args) {
        Leetcode583 code = new Leetcode583();
        System.out.println(code.minDistance("leetcode","etco"));//结果4   
        //第一个字符串长度(8)-公共子序列(4) + 4-4 = 4
        System.out.println(code.minDistance("eat","sea"));//结果2
        //3 - 2 + 3 -2 = 2
        System.out.println(code.minDistance("park","spake"));//结果3
        //公共子序列并没有要求连续4-3 + 5-3 = 3
        
    }
    public int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length
            //字符串的charAt方法得分效率不好
            //改进
        char[] chars1 = word1.toCharArray();
        char[] chars2 = word2.toCharArray();
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i < m + 1; i++) {
            int x = chars1[i - 1];
            for (int j = 1; j < n + 1; j++) {
                int y = chars2[j - 1];
                if (x == y) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Integer.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return m + n - dp[m][n] - dp[m][n];
    }
}

10) 最长上升子序列-Leetcode 300

/*
                    1       2       3       4
            1       3       6       4       9
            1       13      16      14      19
                            136     134     139
                                            169
                                            1369
                                            149
                                            1349
           (1)    (2)      (3)     (3)      (4)
                                            4
     */

public class Leetcode300 {
    
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);
        for (int i = 1; i < nums.length; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) { // 满足了升序条件
                    // 用之前递增子序列的最大长度 + 1 更新当前长度
                    dp[i] = Integer.max(dp[i], dp[j] + 1);
                }
            }
            System.out.println(Arrays.toString(dp));
        }
        return Arrays.stream(dp).max().getAsInt();
    }

    public static void main(String[] args) {
        Leetcode300 code = new Leetcode300();
        System.out.println(code.lengthOfLIS(new int[]{1, 3, 6, 4, 9}));
//        System.out.println(code.lengthOfLIS(new int[]{10, 9, 2, 5, 3, 7, 101, 18}));
//        System.out.println(code.lengthOfLIS(new int[]{1, 3, 6, 7, 9, 4, 10, 5, 6}));
        //                                            1 3 6 7 9 10  = 6
        //                                            1 3 4 5 6     = 5
//        System.out.println(code.lengthOfLIS(new int[]{0, 1, 0, 3, 2, 3}));
//        System.out.println(code.lengthOfLIS(new int[]{7, 7, 7, 7, 7, 7, 7}));
    }
}

并不是返回最后一个元素,所以我们要遍历整个数组找到最大值然后转化为整数.

Leetcode-96 不同的二叉搜索树

我们把n个节点所能组成的二叉搜索树的总和称之为卡特兰数

11) Catalan 数

public class Catalan {
    public static void main(String[] args) {
        System.out.println(catalan(6));
    }

    static int catalan(int n) {
        //for(int i = 0;i<n;i++){
         //   System.out.println("(%d,%d)\t",i,n-1-i);
      //  }
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i < n + 1; i++) {
            for (int j = 0; j < i; j++) {//第i个卡特兰数
                System.out.print("(" + j + " " + (i - 1 - j) + ")\t");
                dp[i] += dp[j] * dp[i - 1 - j];
            }
            System.out.println();
            System.out.println(Arrays.toString(dp));
        }
        return dp[n];
    }
}

class Solution {
    public int numTrees(int n) {
        //左边节点比父节点小  右边节点比父节点大
        //本质是求 第n个卡特兰数
        int[] dp = new int[n+1];//为什么+1因为要从0开始
        dp[0]=1;
        dp[1]=1;//由一个节点组成的值
        for(int i=2;i<n+1;i++){
            for(int j=0;j<i;j++){
                dp[i]+=dp[j]*dp[i-j-1];//第i个卡特兰数的拆分
            }
        }
        return dp[n];


    }
}

Catalan数应用-出栈总数

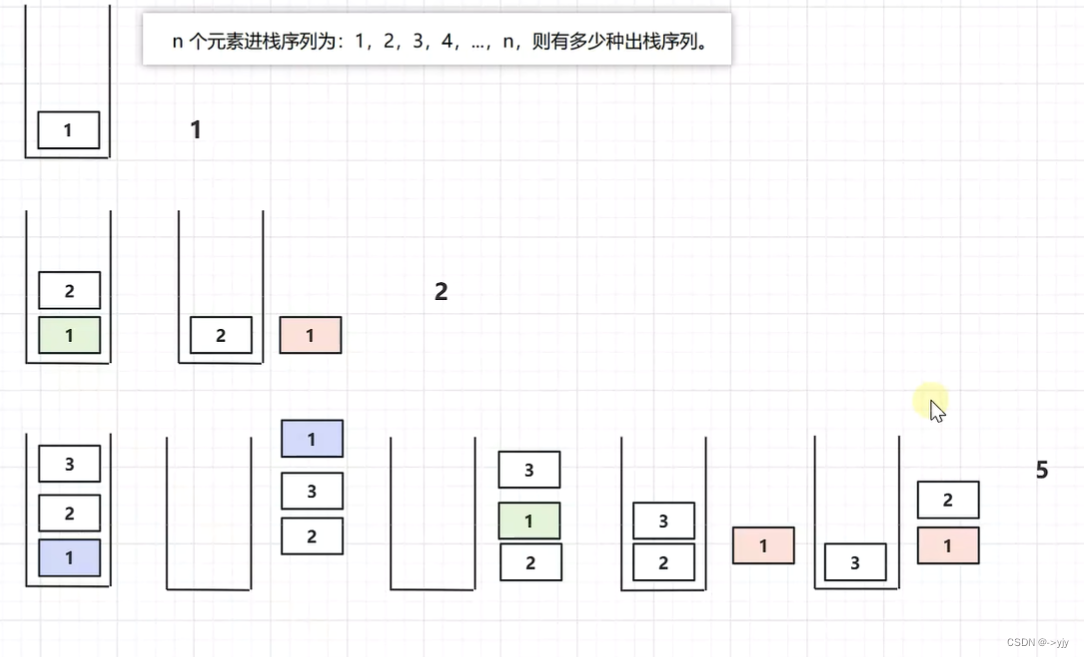
4个元素 ==> 14 

Leetcode-22 括号生成

三对括号: 

public class Leetcode22 {

    public List<String> generateParenthesis(int n) {
        ArrayList<String>[] dp = new ArrayList[n + 1];
        dp[0] = new ArrayList<>(List.of(""));
        dp[1] = new ArrayList<>(List.of("()"));
        for (int j = 2; j < n + 1; j++) {
            dp[j] = new ArrayList<>();
            for (int i = 0; i < j; i++) { // 第j个卡特兰数的拆分
                //i 对应的集合是内层要嵌套的括号,j-1-i对应的集合是平级要拼接的括号
                System.out.printf("(%d,%d)\t", i, j - 1 - i);
//                dp[j] += dp[i] * dp[j - 1 - i];
//                dp[j].add("(" + dp[i] + ")" + dp[j - 1 - i]);
                for (String k1 : dp[i]) {
                    for (String k2 : dp[j - 1 - i]) {
                        dp[j].add("(" + k1 + ")" + k2);
                    }
                }
            }
            System.out.println(dp[j]);
        }
        return dp[n];
    }

    public static void main(String[] args) {
        Leetcode22 code = new Leetcode22();
        System.out.println(code.generateParenthesis(4));
    }
}

买票找零问题

售票处售卖球票，每张票 50 元。有2n人前来买票

• 其中一半人手持 50 元钞票

• 另一半人手持 100 元钞票

若售票处开始没有任何零钱，问：有多少种排队方式，能够让售票顺畅进行。

思路：

• 把手持 50 元钞票的人视为左括号

• 把手持 100 元钞票的人视为右括号

• 左右括号合法配对，即先出现左括号，再出现右括号，就可以让售票顺畅执行

可以看到，问题又变成了求解 n 的卡特兰数

331. 验证二叉树的前序序列化 - 力扣（LeetCode）

用栈解决:

import java.util.Stack;

public class Solution {
    public boolean isValidSerialization(String preorder) {
        Stack<String> stack = new Stack<>();
        for (String node : preorder.split(",")) {
            stack.push(node);
            while (stack.size() >= 3 && stack.get(stack.size() - 1).equals("#") && stack.get(stack.size() - 2).equals("#") && !stack.get(stack.size() - 3).equals("#")) {
                stack.pop();
                stack.pop();
                stack.pop();
                stack.push("#");
            }
        }
        return stack.size() == 1 && stack.pop().equals("#");
    }
}

出入度

public class Solution {
    public boolean isValidSerialization(String preorder) {
        String[] nodes = preorder.split(",");
        int diff = 1;
        for (String node : nodes) {
            diff -= 1;
            if (diff < 0) {
                return false;
            }
            if (!node.equals("#")) {
                diff += 2;
            }
        }
        return diff == 0;
    }
}

class Solution {
    public boolean isValidSerialization(String preorder) {
        List<String> stk = new ArrayList<>();
        for (String s : preorder.split(",")) {
            stk.add(s);
            while (stk.size() >= 3 && stk.get(stk.size() - 1).equals("#")
                && stk.get(stk.size() - 2).equals("#") && !stk.get(stk.size() - 3).equals("#")) {
                stk.remove(stk.size() - 1);
                stk.remove(stk.size() - 1);
                stk.remove(stk.size() - 1);
                stk.add("#");
            }
        }
        return stk.size() == 1 && stk.get(0).equals("#");
    }
}

894. 所有可能的真二叉树 - 力扣（LeetCode）

class Solution {
    public List<TreeNode> allPossibleFBT(int n) {
        return process(n);
    }

    public List<TreeNode>process(int n){
        List<TreeNode>res = new ArrayList<>();
        if(n==1){
            res.add(new TreeNode(0));
            return res;
        }

        if(n%2==0){
            return res;
        }

        for(int i =1;i<n;i+=2){
            List<TreeNode>leftInfo = process(i);
            List<TreeNode>rightInfo = process(n-1-i);
            for(TreeNode l:leftInfo){
                for(TreeNode r:rightInfo){
                    TreeNode node = new TreeNode(0,l,r);
                    res.add(node);
                }
            }
        }
        return res;
    }
}

12) 打家劫舍-Leetcode 198

价值                0        1        2        3        4

                       0        0        0        0        0

        0(2)         2        0        0        0        0

        1(7)         2        7        0        0        0

        2(9)         2        7        9+2     0       0

        3(3)         2        7        11        11     0

        4(1)         2        7       11        11      12  

dp[4] = dp[2] + 1 = 12

dp[3] = max(dp[1] + 3,dp[2]) = max(10,11) = 11

dp[i] = max(dp[i-2]+value,dp[i-1]);

public int rob(int[] nums) {
        int len = nums.length;
        if (len == 1) {
            return nums[0];
        }
        int[] dp = new int[len];
        dp[0] = nums[0];
        dp[1] = Integer.max(nums[0], nums[1]);
        for (int i = 2; i < len; i++) {
            dp[i] = Integer.max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[len - 1];
    }

    public static void main(String[] args) {
        HouseRobberLeetcode198 code = new HouseRobberLeetcode198();
        System.out.println(code.rob(new int[]{2, 7, 9, 3, 1}));
        System.out.println(code.rob(new int[]{2, 1, 1, 2}));
    }

13) Travelling salesman problem

旅行商问题

现在假设有四个城市,可以有多个城市,我们以四个为例子

城市到城市之间有一定花费,你是一个旅行商人,你要到这些城市去售卖商品,所有路线你都得经历一遍,请问那条路线花费最少?

不要跟最短路径混淆:最短路径是点到点,或者多源,但是不要求经历所有城市

/*

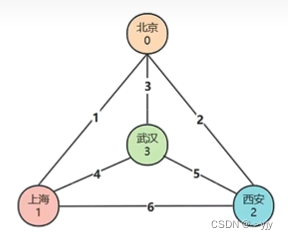
北京 ->

上海 ->

武汉 ->

西安 ->

                3x2 = 6 

北京->上海->

                        武汉-> 西安 ->北京

                        西安->武汉 ->北京

          武汉->

                       上海->西安->北京

                        西安->上海->北京

            西安->

                        上海-> 武汉->北京

                        武汉->上海->北京

5个城市 ==>4x3x2 = 24

6            ==> 5x4x3x2=120

...

(n-1) !  所以一般我们对于旅行商问题没有什么特别好的解决方法

小数据量可以用动态规划求最优解

更大数据量只能求近似解

/*
        北京->
        上海->
        武汉->
        西安->

        4x3x2 = 24
        5x4x3x2 = 120
        ...
        (n-1)!
        北京->上海->
                  武汉->西安->北京
                  西安->武汉->北京
             西安->
                  上海->武汉->北京
                  武汉->上海->北京
             武汉->
                  上海->西安->北京
                  西安->上海->北京

         g
              0  1  2  3
          0  {0, 1, 2, 3}
          1  {1, 0, 6, 4}
          2  {2, 6, 0, 5}
          3  {3, 4, 5, 0}

          d(出发城市, 剩余城市集合) ==> 从出发城市开始，走完剩余城市，花费的最少代价
          d(0,1|2|3) => g[0][1] + d(1,2|3) => g[1][3] + d(3,2) => g[3][2] + d(2,空)
                                                                            g[2][0]
                                           => g[1][2] + d(2,3) => g[2][3] + d(3,空)
                                                                            g[3][0]
                        g[0][2] + d(2,1|3) => g[2][1] + d(1,3) => g[1][3] + d(3,空)
                                                                            g[3][0]
                                           => g[2][3] + d(3,1) => g[3][1] + d(1,空)
                                                                            g[1][0]
                        g[0][3] + d(3,1|2) => g[3][1] + d(1,2) => g[1][2] + d(2,空)
                                                                            g[2][0]
                                           => g[3][2] + d(2,1) => g[2][1] + d(1,空)
                                                                            g[1][0]
                0   1   2   3    4   5    6    7     j 剩余城市集合
                0   1   2   1|2  3   1|3  2|3  1|2|3
           0
           1
           2
           3
           i 出发城市
            
            //用二进制表示城市组合

           000 没城市  0
           001 1号    1
           010 2号    2
           100 3号    4
           011 1和2   3
           101 1和3   5
           110 2和3   6
           111 1和2和3 7

          出发城市 i
          剩余城市集合 j
            遍历 j 时的变量 k （剩余的某一个城市)
          d(i, j) => min(
                        g[i][k] + d(k, j去掉k)
                        g[i][k] + d(k, j去掉k)
                        g[i][k] + d(k, j去掉k)
                    )
          d(k,空) => 从k回到起点 => g[k][i]


          d(0,1|2) => g[0][1] + d(1,2)
                   => g[0][2] + d(2,1)
          d(1,1|2)
          d(2,1|2)
          d(3,1|2) => g[3][1] + d(1,2)
                   => g[3][2] + d(2,1)
     */

import java.util.Arrays;
import java.util.stream.Collectors;

/**
 * <h3>旅行商问题</h3>
 */
public class TravellingSalesmanProblem {

    

    public static void main(String[] args) {
        int[][] graph = {
                {0, 1, 2, 3},
                {1, 0, 6, 4},
                {2, 6, 0, 5},
                {3, 4, 5, 0},
        };
        System.out.println(tsp(graph));
    }

    static int tsp(int[][] g) {
        int m = g.length; // 城市数目
        int n = 1 << (m - 1); // 剩余城市的组合数  2^(m-1)
        int[][] dp = new int[m][n];

        // 填充第0列
        for (int k = 0; k < m; k++) {
            dp[k][0] = g[k][0];
        }
        print(dp);

        // 填充后续列
        for (int j = 1; j < n; j++) {
            for (int i = 0; i < m; i++) {
                dp[i][j] = Integer.MAX_VALUE / 2;
                if(contains(j, i)) continue; // 剩余城市集合已包含出发城市，不合理
                // 填充单元格
                for (int k = 0; k < m; k++) {
                    if(contains(j, k)) { // 只对剩余城市集合中的城市进行处理
                        dp[i][j] = Integer.min(dp[i][j], g[i][k] + dp[k][exclude(j, k)]);
                    }
                }
            }
        }
        print(dp);
        return dp[0][n - 1];
    }

    /*
        2|3
        110  城市1是否存在    110
                           001 &
                           ----
                           000
                           false
        110  城市2是否存在    011
                           001 &
                           ----
                           001
                           true
        110  城市3是否存在    001
                           001 &
                           ----
                           001
                           true
        110  城市4是否存在    000
                           001 &
                           ----
                           000
                           false

     */
    static boolean contains(int set, int city) {
        return (set >> (city - 1) & 1) == 1;
    }

    /*
        1|2|3  1 => 2|3

        111
        001 ^
        ----
        110     2|3

        1|2|3  2 => 1|3
        111
        010 ^
        ----
        101   1|3
     */
    static int exclude(int set, int city) {
        return set ^ (1 << (city - 1));
    }

    static void print(int[][] dist) {
        System.out.println("-------------------------");
        for (int[] row : dist) {
            System.out.println(Arrays.stream(row).boxed()
                    .map(x -> x >= Integer.MAX_VALUE / 2 ? "∞" : String.valueOf(x))
                    .map(s -> String.format("%2s", s))
                    .collect(Collectors.joining(",", "[", "]")));
        }
    }
}

 public static void main(String[] args) {
        int[][] graph = {
                {0, 1, 2, 3},
                {1, 0, 6, 4},
                {2, 6, 0, 5},
                {3, 4, 5, 0},
        };
//        System.out.println(tsp(graph));
        System.out.println(6 >> (0-1));
    }

    static int tsp1(int[][] graph) {
        int n = graph.length;
        int[][] dp = new int[1 << n][n];
        for (int[] row : dp) {
            Arrays.fill(row, Integer.MAX_VALUE / 2);
        }
        dp[1][0] = 0;
        for (int mask = 1; mask < 1 << n; mask++) {
            for (int i = 0; i < n; i++) {
                if ((mask & 1 << i) == 0) continue;
                for (int j = 0; j < n; j++) {
                    if ((mask & 1 << j) != 0) continue;
                    dp[mask | 1 << j][j] = Math.min(dp[mask | 1 << j][j], dp[mask][i] + graph[i][j]);
                }
            }
            print(dp);
        }

        int res = Integer.MAX_VALUE;
        for (int i = 0; i < n; i++) {
            res = Math.min(res, dp[(1 << n) - 1][i] + graph[i][0]);
        }
        return res;
    }

    /*
        110 是否包含 0 = 0 & 1 = 0
        110 是否包含 1 = 110 & 1 = 0
        110 是否包含 2 = 11 & 1 = 1
        110 是否包含 3 = 1 & 1 = 1
        110 是否包含 4 = 0 & 1 = 0
     */
    static boolean contains(int set, int city) {
        return (set >> (city - 1) & 1) == 1;
    }

    /*
       
    
        110     110
       ^100    ^010
       ----    ----
         10     100

     */
    static int exclude(int set, int city) {
        return set ^ (1 << (city - 1));
    }

    static int tsp(int[][] g) {
        int n = g.length;
        int m = 1 << (n - 1);
        int[][] dp = new int[n][m];
        for (int i = 0; i < n; i++) {
            dp[i][0] = g[i][0];
        }
        for (int j = 1; j < m; j++) {
            for (int i = 0; i < n; i++) {
                dp[i][j] = Integer.MAX_VALUE / 2;
                if (contains(j, i)) continue;
                for (int k = 1; k < n; k++) {
                    if (contains(j, k)) {
//                    System.out.println("(" + k + "," + (j ^ (1 << (k - 1))) + ")");
                        dp[i][j] = Math.min(dp[i][j], g[i][k] + dp[k][exclude(j, k)]);
                    }
                }
            }
            print(dp);
        }

        return dp[0][m - 1];
    }

    static void print(int[][] dist) {
        System.out.println("-------------------------");
        for (int[] row : dist) {
            System.out.println(Arrays.stream(row).boxed()
                    .map(x -> x >= Integer.MAX_VALUE / 2 ? "∞" : String.valueOf(x))
                    .map(s -> String.format("%2s", s))
                    .collect(Collectors.joining(",", "[", "]")));
        }
    }

其它题目

题号	标题
无	集合覆盖问题
无	扔鸡蛋问题
Leetcode 72	编辑距离
Leetcode 121	买股票的最佳时机

72. 编辑距离 - 力扣（LeetCode）

class Solution {
    public int minDistance(String word1, String word2) {
        int n1 = word1.length();
        int n2 = word2.length();
        int[][] dp = new int[n1+1][n2+1];
        //第一行
        for(int j =1;j<=n2;j++)dp[0][j] = dp[0][j-1]+1;
        //第一列
        for(int i =1;i<=n1;i++)dp[i][0] = dp[i-1][0] + 1;
        for(int i = 1;i<=n1;i++){
            for(int j = 1;j<=n2;j++){
                if(word1.charAt(i-1)==word2.charAt(j-1))dp[i][j] = dp[i-1][j-1];
                else dp[i][j] = Math.min(Math.min(dp[i-1][j-1],dp[i][j-1]),dp[i-1][j])+1;

            }
        }
        return dp[n1][n2];
    }
}

121. 买卖股票的最佳时机 - 力扣（LeetCode）

class Solution {
    public int maxProfit(int[] prices) {
        int cost = Integer.MAX_VALUE,profit = 0;
        for(int price:prices){
            cost = Math.min(cost,price);
            profit=Math.max(profit,price-cost);
        }
        return profit;
    }
}