贝叶斯优化是一种处理黑盒函数优化问题的重要方法。它通过构建一个目标函数的代理模型,并且利用贝叶斯机器学习方法如高斯过程回归来评估代理模型的不确定性。基于代理模型,通过一个采样函数来决定在哪里进行采样。本推文简单描述了贝叶斯优化方法的框架,包括高斯过程回归和三种常用的采样函数:期望提升,知识梯度,熵搜索和预测熵搜索。最后,本文提供了一些常用的高斯过程回归和贝叶斯优化的软件包。
1.贝叶斯优化问题
贝叶斯优化常用于求解如下的优化问题:
max
x
∈
A
f
(
x
)
\begin{equation} \max_{x\in\mathcal{A}}f(x) \end{equation}
x∈Amaxf(x)
其中可行解和目标函数通常具备如下的特征:
1.解空间的维度不会太高,通常 d ≤ 20 d\leq 20 d≤20;
2.可行域 A \mathcal{A} A是一个简单的集合;
3.目标函数 f f f具有一定的连续性,可以用高斯过程回归(GPR)建模;
4. f f f的采样成本很高,对 f f f的采样次数通常是有限的;
5. f f f是黑盒函数,其结构信息例如凸性或线性性是未知的;
6.采样 f f f时只能观测到函数值,无法观测到一阶梯度或者二阶信息;
7.采样 f f f时观测值可以是无噪声的,也可以是有噪声的并假设噪声是相互独立的;
8.需要求解全局最优解。
总结起来,贝叶斯优化是一种用于解决无梯度信息下全局黑盒函数优化问题的方法。在下文分析中,我们假设 f f f的观测值是无噪声的。
2.算法框架
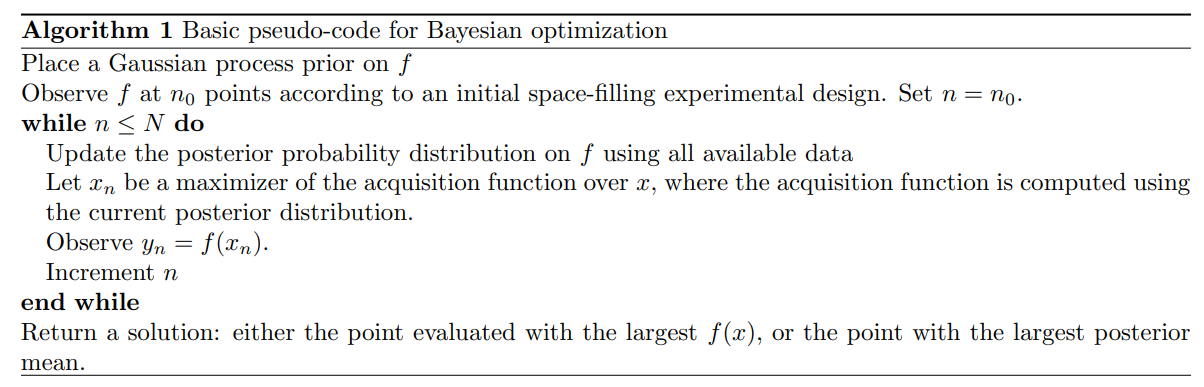
贝叶斯优化算法框架包含两个重要的部分:1.贝叶斯统计模型来建模目标函数;2.采样函数来决定下一次迭代在哪里采样(参见Algorithm1)。
通常选取高斯过程回归作为统计模型,其通过贝叶斯后验概率分布来描述函数值 f ( x ) f(x) f(x)。每次迭代时,我们观测到一个 f ( x ) f(x) f(x)的函数值并更新后验分布。采样函数基于 f f f当前的后验分布来计算在一个新的点 x x x处采样可能获得的价值。
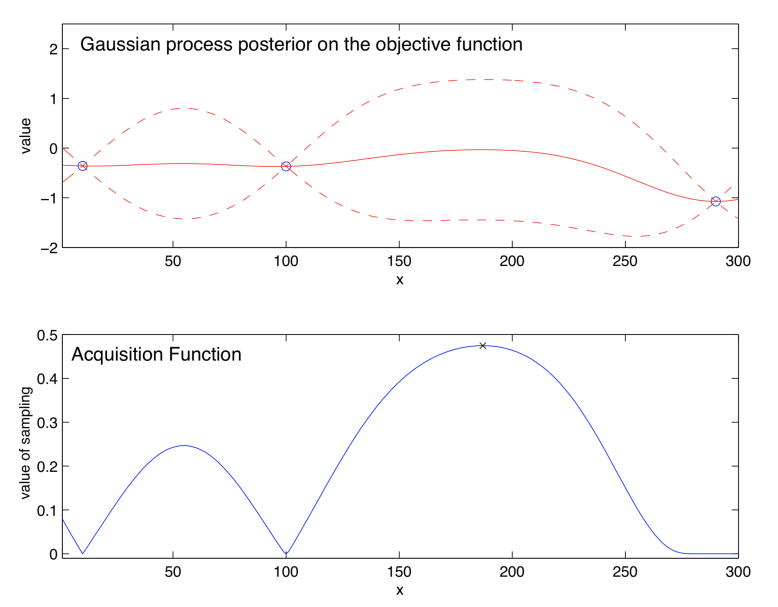
下图展示了贝叶斯优化算法的一次迭代过程,其使用高斯过程回归作为统计模型并使用期望提升(experceted improvement)作为采样函数。上半部分展示了在得到三个无噪声的采样点后,利用高斯过程回归得到的对目标函数的估计,实现可以理解为对于 f ( x ) f(x) f(x)的点估计,虚线区域代表了可信区间(credible interval),类似于频率统计当中的置信区间。下半部分图当前的后验分布对应的采样函数的值,对于已采样的点,由于观测值不含噪声,再次这些点无法提供新的信息,因此相应的采样函数值为0,对于可信区域较大区间的点,由于其函数值具有较高的不确定性,采样该点具有更大的价值,采样函数的值也相对较大。
3.高斯过程回归
高斯过程回归是一种用于建模函数的贝叶斯方法,该方法的详细的介绍可参考文献[3]。对于有限的点
x
1
,
.
.
.
,
x
k
∈
R
d
x_1,...,x_k\in \mathbb{R}^d
x1,...,xk∈Rd和对应函数值向量
[
f
(
x
1
)
,
.
.
.
,
f
(
x
k
)
]
[f(x_1),...,f(x_k)]
[f(x1),...,f(xk)],高斯过程回归假设先验分布为正态分布:
f
(
x
1
:
k
)
∼
N
(
μ
0
(
x
1
:
k
)
,
Σ
0
(
x
1
:
k
,
x
1
:
k
)
)
f(x_{1:k})\sim N(\mu_0(x_{1:k}),\Sigma_0(x_{1:k},x_{1:k}))
f(x1:k)∼N(μ0(x1:k),Σ0(x1:k,x1:k))
其中,
x
1
:
k
x_{1:k}
x1:k表示
x
1
,
.
.
.
,
x
k
x_1,...,x_k
x1,...,xk,
f
(
x
1
:
k
)
=
[
f
(
x
1
)
,
.
.
.
,
f
(
x
k
)
]
f(x_{1:k})=[f(x_1),...,f(x_k)]
f(x1:k)=[f(x1),...,f(xk)],
Σ
0
(
⋅
,
⋅
)
\Sigma_0(\cdot,\cdot)
Σ0(⋅,⋅)表示协方差函数或核函数,我们可以通过选择
Σ
0
\Sigma_0
Σ0来加入一些先验知识,例如在输入空间中距离更近的
x
i
,
x
j
x_i,x_j
xi,xj对应的函数值有很大的正相关性。
假设我们有无噪声的观测值
[
f
(
x
1
)
,
.
.
.
,
f
(
x
n
)
]
[f(x_1),...,f(x_n)]
[f(x1),...,f(xn)],我们想推断未观测点
x
x
x的函数值
f
(
x
)
f(x)
f(x),利用贝叶斯规则,我们有:
f
(
x
)
∣
f
(
x
1
:
n
)
∼
N
(
μ
n
(
x
)
,
σ
n
2
(
x
)
)
μ
n
(
x
)
=
Σ
0
(
x
,
x
1
:
n
)
Σ
0
(
x
1
:
n
,
x
1
:
n
)
−
1
(
f
(
x
1
:
n
)
−
μ
0
(
x
1
:
n
)
)
+
μ
0
(
x
)
σ
n
2
=
Σ
0
(
x
,
x
)
−
Σ
0
(
x
,
x
1
:
n
)
Σ
0
(
x
1
:
n
,
x
1
:
n
)
−
1
Σ
0
(
x
1
:
n
,
x
)
\begin{aligned} &f(x)|f(x_{1:n})\sim N(\mu_n(x),\sigma^2_{n}(x))\\ &\mu_n(x)=\Sigma_0(x,x_{1:n})\Sigma_0(x_{1:n},x_{1:n})^{-1}(f(x_{1:n})-\mu_0(x_{1:n}))+\mu_0(x)\\ &\sigma^2_n = \Sigma_0(x,x)-\Sigma_0(x,x_{1:n})\Sigma_0(x_{1:n},x_{1:n})^{-1}\Sigma_0(x_{1:n},x) \end{aligned}
f(x)∣f(x1:n)∼N(μn(x),σn2(x))μn(x)=Σ0(x,x1:n)Σ0(x1:n,x1:n)−1(f(x1:n)−μ0(x1:n))+μ0(x)σn2=Σ0(x,x)−Σ0(x,x1:n)Σ0(x1:n,x1:n)−1Σ0(x1:n,x)
后验均值
μ
n
(
x
)
\mu_n(x)
μn(x)是先验信息和样本信息的加权,其权重依赖于核函数
Σ
0
\Sigma_0
Σ0。
常用的核函数及其超参优化方法可以参考文献[3]的第四、五章。
4.采样函数
在贝叶斯优化算法中,采样函数用于决定下一步对定义域A中的哪个采样点。常用的采样函数包括:期望提升,知识梯度,以及熵搜索和预测熵搜索。本节简单介绍不同采样函数的定义及采样准则。
4.1 期望提升(Expected Improvement)
假设我们只能返回之前采样过的点 x x x作为优化问题的解,并且在采样次数用完之后必须基于之前的观测值返回一个解。由于假设 f f f的观测值是无噪声的,最优的选择是先前采样过的点当中观测值最大的。记 f n ∗ = max m ≤ n f ( x m ) f^{*}_{n}=\max_{m\leq n}f(x_m) fn∗=maxm≤nf(xm)为最终选择的解的函数值,其中 n n n表示目前采样 f f f的次数。
假设我们有一次额外的采样机会,如果对 x ∈ A x \in \mathcal{A} x∈A采样,则我们将观测到 f ( x ) f(x) f(x)。在采样之后,会出现两种情况: f ( x ) ≥ f n ∗ f(x)\geq f_n^{*} f(x)≥fn∗和 f ( x ) ≤ f n ∗ f(x)\leq f_{n}^{*} f(x)≤fn∗。对于前者,最优值的提升为 f ( x ) − f n ∗ f(x)-f_n^{*} f(x)−fn∗;对于后者,提升为0。我们将提升记作 [ f ( x ) − f n ∗ ] + [f(x)-f^{*}_n]^{+} [f(x)−fn∗]+,其中 a + = max ( a , 0 ) a^{+}=\max(a,0) a+=max(a,0)。定义期望提升如下: E I n = E [ [ f ( x ) − f n ∗ ] + ] ] EI_{n} = \mathbb{E}[[f(x)-f^{*}_n]^{+}]] EIn=E[[f(x)−fn∗]+]]
利用分部积分可以得到一个闭式形式:
E
I
n
(
x
)
=
[
△
n
(
x
)
]
+
+
σ
n
(
x
)
φ
(
△
n
(
x
)
σ
n
(
x
)
)
−
∣
△
n
(
x
)
∣
Φ
(
△
n
(
x
)
σ
n
(
x
)
)
EI_{n}(x)=[\triangle_n(x)]^{+}+\sigma_n(x)\varphi(\frac{\triangle_n(x)}{\sigma_n(x)})-|\triangle_n(x)|\Phi(\frac{\triangle_n(x)}{\sigma_n(x)})
EIn(x)=[△n(x)]++σn(x)φ(σn(x)△n(x))−∣△n(x)∣Φ(σn(x)△n(x))
其中,
△
n
(
x
)
=
μ
n
(
x
)
−
f
n
∗
\triangle_n(x)=\mu_n(x)-f_n^*
△n(x)=μn(x)−fn∗。然后,EI算法选择EI最大的点作为下一步的采样点,即:
x
n
+
1
=
arg
max
E
I
n
(
x
)
x_{n+1}=\arg \max EI_n(x)
xn+1=argmaxEIn(x)
下图显示了
E
I
n
(
x
)
EI_n(x)
EIn(x)与
△
n
(
x
)
\triangle_n(x)
△n(x),
σ
n
(
x
)
\sigma_n(x)
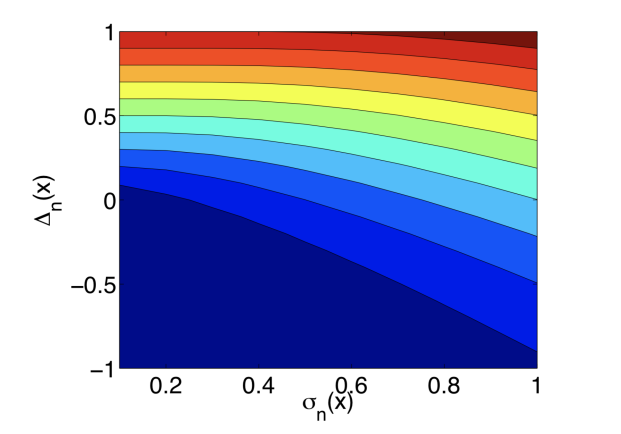
σn(x)之间的单增关系。其中蓝色代表更小的值且红色代表更大的值。
E
I
n
(
x
)
EI_n(x)
EIn(x)关于
△
n
(
x
)
\triangle_n(x)
△n(x)和
σ
n
(
x
)
\sigma_n(x)
σn(x)都是单增的。EI算法偏好于期望效用高的点和不确定性高的点,这体现了探索和利用(exploration vs. exploitation)的权衡。
4.2 知识梯度(Knowledge Gradient)
和期望提升采样函数不同,知识梯度采样函数允许返回任何的点作为问题的解。在风险中性的情况下,最终返回的解
x
∗
^
\hat{x^*}
x∗^为
μ
n
\mu_n
μn最大的点,即
μ
n
(
x
∗
^
)
=
max
x
′
μ
n
(
x
′
)
=
μ
n
∗
\mu_n(\hat{x^*})=\max_{x^{\prime}}\mu_n(x^{\prime})=\mu_n^{*}
μn(x∗^)=maxx′μn(x′)=μn∗。如果可以对一个新的点
x
x
x采样,将会得到后验均值
μ
n
+
1
\mu_{n+1}
μn+1,在新的后验均值下,最后一步采样得到的函数值提升为
μ
n
+
1
∗
−
μ
n
∗
\mu^{*}_{n+1}-\mu^*_n
μn+1∗−μn∗。定义知识梯度为:
K
G
n
(
x
)
=
E
n
[
μ
n
+
1
∗
−
μ
n
∗
∣
x
n
+
1
=
x
]
KG_n(x)=\mathbb{E}_n[\mu^*_{n+1}-\mu^*_{n}|x_{n+1}=x]
KGn(x)=En[μn+1∗−μn∗∣xn+1=x]
下一步的采样点为:
x
n
+
1
=
arg
max
K
G
n
(
x
)
x_{n+1}=\arg \max KG_n(x)
xn+1=argmaxKGn(x)

算法2给出了一种通过仿真计算知识梯度的方法。每次迭代时,算法仿真一个在点 x x x处采样后可能得到的观测值 y n + 1 y_{n+1} yn+1, 然后基于仿真结果 ( x , y n + 1 ) (x,y_{n+1}) (x,yn+1)计算 μ n + 1 ∗ \mu^{*}_{n+1} μn+1∗并得到KG的一个估计值,重复上述迭代过程 J J J次将得到的估计值的均值作为对KG的估计,当 J J J趋于无穷时估计值将会收敛到 K G n ( x ) KG_n(x) KGn(x)。
算法2可以被用来估计 K G n ( x ) KG_n(x) KGn(x)并结合零阶优化算法来得到采样函数的最大值点。为了提升算法效率,Wu J, Frazier P.(2009)提出了一种基于多起点的随机梯度上升的方法来优化采样函数,具体细节参考文献[2]。
算法3提出了一种方法来优化KG采样函数来得到下一步的采样点,其中算法3内部循环中使用的随机梯度G由算法4计算得到。


不同于EI仅考虑被采样点的后验分布,KG考虑了函数 f f f的后验分布以及采样点如何影响后验分布。KG会采样那些使得后验均值的最大值得到提升的采样点即使采样点本身并不比之前采样过的最优点更好。在带有观测值带有噪声的贝叶斯优化问题当中,KG能够带来明显的性能提升。
4.3 熵搜索和预测熵搜索(Entropy Search and Predictive Entropy Search)
一个连续的概率分布 p ( x ) p(x) p(x) 的微分熵(differential entropy)定义为 ∫ p ( x ) l o g ( p ( x ) ) d x \int p(x)log(p(x))dx ∫p(x)log(p(x))dx, 更小的微分熵意味着更小的不确定性。熵搜索(ES)算法每次迭代时对使得微分熵降低最大的点进行采样。预测熵搜索(PES)算法的想法相同,但是使用了不同的优化目标。精确计算PES和ES将会得到等价的采样函数。但是精确计算通常是不可行的,因此近似计算方法的不同导致了两种算法的采样决策也有差异。
令
x
∗
x^*
x∗为
f
f
f的全局最优解。第n次迭代,高斯过程后验为
x
∗
x^*
x∗诱导了一个概率分布,记
H
(
P
n
(
x
∗
)
)
H(P_n(x^*))
H(Pn(x∗))为在该分布下计算得到的熵。类似地,如果对
x
x
x进行采样,则
H
(
P
n
(
x
∗
∣
x
,
f
(
x
)
)
)
H(P_n(x^*|x,f(x)))
H(Pn(x∗∣x,f(x)))表示第n+1次迭代时的熵。通过采样
x
x
x使得熵的减少为:
E
S
n
(
x
)
=
H
(
P
n
(
x
∗
)
)
−
E
f
(
x
)
[
H
(
P
n
(
x
∗
∣
f
(
x
)
)
)
]
ES_n(x)=H(P_n(x^*))-E_{f(x)}[H(P_n(x^*|f(x)))]
ESn(x)=H(Pn(x∗))−Ef(x)[H(Pn(x∗∣f(x)))]
ES可以被近似地计算和优化。PES提供了另一种方法来计算前一行的公式,由于
f
(
x
)
f(x)
f(x)导致
x
∗
x^*
x∗的熵减少等于
f
(
x
)
f(x)
f(x)和
x
∗
x^*
x∗之间的相互信息:
P
E
S
n
(
x
)
=
E
S
n
(
x
)
=
H
(
P
n
(
f
(
x
)
)
)
−
E
x
∗
[
H
(
P
n
(
f
(
x
)
∣
x
∗
)
)
]
PES_n(x)=ES_n(x)=H(P_n(f(x)))-E_{x^*}[H(P_n(f(x)|x^*))]
PESn(x)=ESn(x)=H(Pn(f(x)))−Ex∗[H(Pn(f(x)∣x∗))]
PES的第一项有解析形式,第二项必须通过近似得到。
5.软件
在本小节中列出了一些贝叶斯优化和高斯过程回归的软件包。
- DiceKriging and DiceOptim (R): 分别是高斯过程回归和贝叶斯优化的软件包,https://cran.r-project.org/web/packages/DiceOptim/index.html
- GPyOpt (Python):基于高斯过程回归包Gpy的贝叶斯优化软件包,https://github.com/SheffieldML/GPyOpt
- Spearmint (Python): 贝叶斯优化软件包
- GPFlow and GPyTorch(python):是分别基于Tensorflow和PyTorch的高斯过程软件包,https://github.com/GPflow/GPflow,https://github.com/cornellius-gp/
- Metrics Optimization Engine (C++): https://github.com/Yelp/MOE
- DACE(Matlab):高斯过程回归软件包,http://www2.imm.dtu.dk/projects/dace/
文献
[1] Frazier P I. A tutorial on Bayesian optimization[J]. arXiv preprint arXiv:1807.02811, 2018.
[2] Wu J, Frazier P. The parallel knowledge gradient method for batch Bayesian optimization[J]. Advances in neural information processing systems, 2016, 29.
[3] Rasmussen, C. and Williams, C. (2006). Gaussian Processes for Machine Learning. MIT Press, Cam bridge, MA.