环境：Windows 10 专业版 + Python 3.9.1 + Anaconda 2020（ 4.8.2）

系列文章：

人工智能与地理大数据实验--出租车GPS数据—时空大数据Python处理基础（一）

人工智能与地理大数据实验--出租车GPS数据—时空大数据Python处理基础（二）

---

目录

五、源码流程分析

（一）、出租车数据的时间完整性评估

（二）、出租车数据的空间完整性评估

（三）、出租车订单出行特征分析

六、实验结果

（一）、出租车数据的时间完整性评估

（二）、出租车数据的空间完整性评估

（三）、出租车订单出行特征分析

---

五、源码流程分析

（一）、出租车数据的时间完整性评估

1.时间字段的处理

利用字符串str方法，把Series对象转换为pandas内置的StringMethods对象，并使用StringMethods对象的slice方法截去字符串切片，传入开始与结束位置的索引，提取前两位字符，从而获取小时信息。

# 把Stime列转换为StringMethods对象，进行切片操作，再赋值给Hour列
data['Hour'] = data['Stime'].str.slice(0,2)
data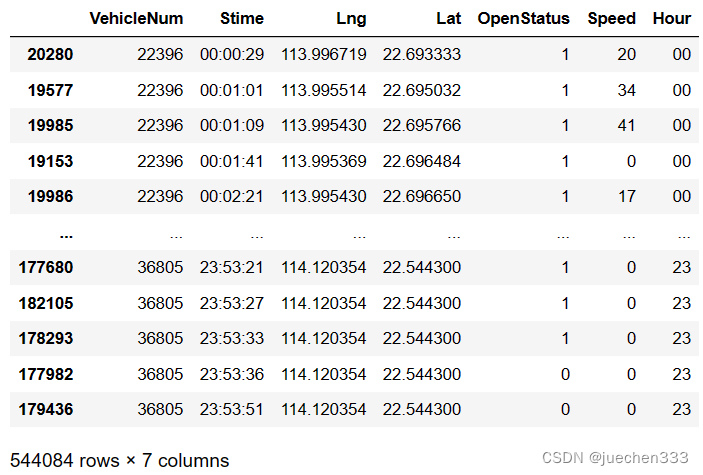

2.数据量的小时集计

同一小时内产生的GPS数据，Hour字段中会拥有相同的值，可以根据这一字段对数据采用groupby方法进行集计操作，再利用count方法指定VehicleNum列统计每小时的数据量。

# 分组并统计各组数量
Hourcount = data.groupby('Hour')['VehicleNum'].count()
# 更改Series的列名，并通过reset_index将Series变成DataFrame
Hourcount = Hourcount.rename('count').reset_index()
Hourcount

3.数据量时间分布的折线图绘制

通过matplotlib库将数据绘制为简单的折线图与柱状图。

# 1.创建图表
# 导入包
import matplotlib.pyplot as plt
# 创建一个图，图的尺寸为8×4in，dpi为300
fig = plt.figure(1,(8,4),dpi = 300)
# 在图中创建子图
# 111分别表示：创建共一个子图，子图的布局为1行1列
ax = plt.subplot(111)

# 2.在图上画
# 绘制折线图，分别传入节点的x坐标与y坐标，'k-'定义了黑色实线
plt.plot(Hourcount['Hour'],Hourcount['count'],'k-')
# 绘制散点图，分别传入节点的x坐标与y坐标，'k.'定义了黑色散线
plt.plot(Hourcount['Hour'],Hourcount['count'],'k.')
# 绘制柱状图，分别传入节点的x坐标与y坐标
plt.bar(Hourcount['Hour'],Hourcount['count'])

# 3.调整图中元素
# 加y轴标题
plt.ylabel('Data volume')
# 加x轴标题
plt.xlabel('Hour')
# 调整x轴标签
plt.xticks(range(24),range(24))
# 加图标题
plt.title('Hourly data volume')
# 设置y轴范围
plt.ylim(0,30000)
# 显示图
plt.show()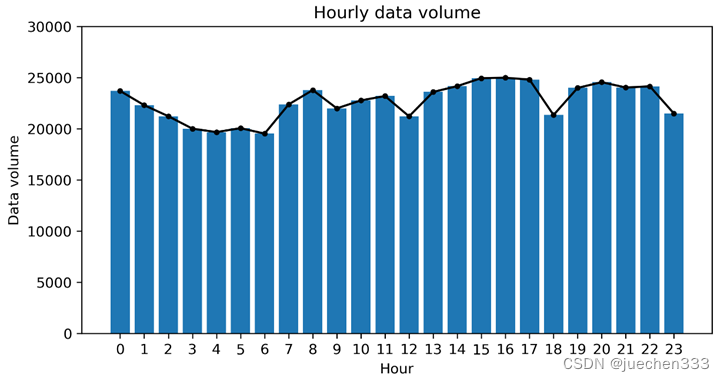

（二）、出租车数据的空间完整性评估

1.出租车GPS数据空间分布栅格图

（1）研究区域栅格生成

用Python代码实现研究范围内栅格，并存储为GeoDataFrame形式。

①研究范围行政区划边界的读取

使用Geopandas读取Shapefile文件

# 导入Geopandas
import geopandas as gpd
# 读取shp格式地理数据文件
sz = gpd.read_file(r'D:\Project\Jupyter_Project\Data\data\sz\sz.shp',encoding = 'utf-8')
# 绘制地理数据文件
sz.plot()

查看读取进来的变量类型及内容

type(sz)

geopandas.geodataframe.GeoDataFrame

sz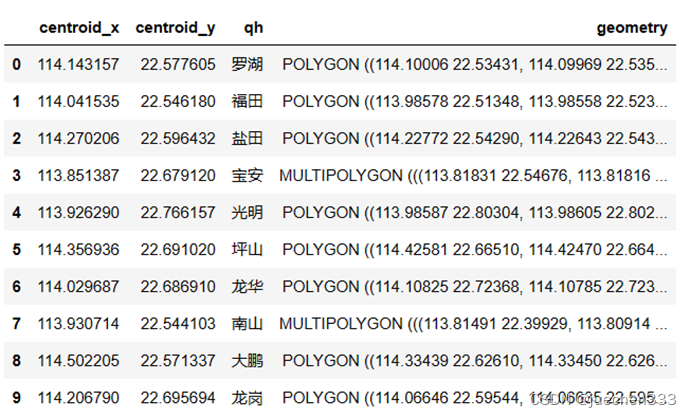

②研究范围内栅格的生成

首先定义研究范围与栅格的大小，计算栅格的△lon与△lat。

# 导入math包
import math
# 划定栅格划分范围
lon1 = 113.75194
lon2 = 114.624187
lat1 = 22.447837
lat2 = 22.864748
# 取得左下角经纬度
latStart = min(lat1,lat2)
lonStart = min(lon1,lon2)
# 定义栅格大小，单位为米
accuracy = 500
# 计算栅格的经纬度增加量大小△Lon和△Lat，地球半径取6371004米
deltaLon = accuracy * 360 / (2 * math.pi * 6371004 * math.cos((lat1 + lat2) * math.pi / 360))
deltaLat = accuracy * 360 / (2 * math.pi * 6371004)
deltaLon,deltaLat

(0.004872614089207591, 0.004496605206422906)

然后，定义一个测试GPS点的经纬度，计算其对应的栅格编号与中心点经纬度。

# 定义一个GPS点测试栅格化
testlon = 114
testlat = 22.5
# 计算该GPS点对应的栅格编号
LONCOL = divmod(float(testlon) - (lonStart - deltaLon / 2), deltaLon)[0]
LATCOL = divmod(float(testlat) - (latStart - deltaLat / 2), deltaLat)[0]
# 计算该GPS点对应的栅格中心点经纬度
# 格子编号*格子宽+起始横坐标=格子中心横坐标
HBLON = LONCOL * deltaLon + lonStart
HBLAT = LATCOL * deltaLat + latStart
LONCOL,LATCOL,HBLON,HBLAT

(51.0, 12.0, 114.00044331854959, 22.501796262477075)

接下来计算每个栅格的四个顶点坐标，循环生成栅格，生成整个研究范围的栅格。

import geopandas as gpd
from shapely.geometry import Polygon
# 定义空的GeoDataFrame表，再往里加栅格
data = gpd.GeoDataFrame()
# 定义空的list，后面循环一次就往里面加东西
LONCOL_list = []
LATCOL_list = []
geometry_list = []
HBLON_list = []
HBLAT_list = []
# 计算行列要生成的栅格数量
# lon方向是lonsum个栅格
lonsnum = int((lon2-lon1) / deltaLon) + 1
# lat方向是latsum个栅格
latsnum = int((lat2-lat1) / deltaLat) + 1
for i in range(lonsnum):
    for j in range(latsnum):
        # 第i列，第j行的栅格中心点坐标
        HBLON = i * deltaLon + lonStart
        HBLAT = j * deltaLat + latStart
        # 用周围的栅格推算三个顶点的位置
        HBLON_1 = (i + 1 ) * deltaLon + lonStart
        HBLAT_1 = (j + 1) * deltaLat + latStart
        # 生成栅格的Polygon形状
        grid_ij = Polygon([
            (HBLON - deltaLon / 2, HBLAT - deltaLat / 2),
            (HBLON_1 - deltaLon / 2, HBLAT - deltaLat / 2),
            (HBLON_1 - deltaLon / 2, HBLAT_1 eltaLat / 2)])
        # 把生成的数据都加入到前面定义的空list里面
        LONCOL_list.append(i)
        LATCOL_list.append(j)
        HBLON_list.append(HBLON)
        HBLAT_list.append(HBLAT)
        geometry_list.append(grid_ij)
# 为GeoPandas文件的每一列赋值为刚刚的list
data['LONCOL'] = LONCOL_list
data['LATCOL'] = LATCOL_list
data['HBLON'] = HBLON_list
data['HBLAT'] = HBLAT_list
data['geometry'] = geometry_list
data

对创建的栅格绘制查看其空间分布。

data.plot(edgecolor = (0,0,0,1),linewidth = 0.2)

利用GeoDataFrame的intersects方法，输入行政区划的Polygon几何图形，将行政区划边界外的栅格剔除。

# 将前面读取的GeoDataFrame用unary_union方法合并为一个Polygon图形作为研究范围
roi = sz.unary_union
# 筛选出研究范围的栅格
grid_sz = data[data.intersects(roi)]
grid_sz.plot(edgecolor = (0,0,0,1),linewidth = 0.2)

将栅格数据保存至本地

grid_sz.to_file(r'D:\Project\Jupyter_Project\Data\data\grid_sz1.josn', driver = 'GeoJSON')

（2）GPS数据的栅格对应与集计

GPS数据以经纬度坐标的形式记录，计算得到每个GPS点对应的栅格编号。然后，再基于栅格标号统计每个栅格内GPS数据量。

import pandas as pd
# 读取数据
data = pd.read_csv('D:/Project/Jupyter_Project/Data/data/TaxiData-Sample.csv',header = None)
data.columns = ['VehicleNum','Stime','Lng','Lat','OpenStatus','Speed']
# 数据对应的栅格经纬度编号
data['LONCOL'] = ((data['Lng'] - (lonStart - deltaLon / 2))/deltaLon).astype('int')
data['LATCOL'] = ((data['Lat'] - (latStart - deltaLat / 2))/deltaLat).astype('int')
# 集计栅格数量
data_distribution = data.groupby(['LONCOL','LATCOL'])['VehicleNum'].count().rename('count').reset_index()
# 剔除不在研究范围内的OD记录
data_distribution = data_distribution[(data_distribution['LONCOL']>=0)&(data_distribution['LATCOL']>=0)&(data_distribution['LONCOL']<=lonsnum)&(data_distribution['LATCOL']<latsnum)]
data_distribution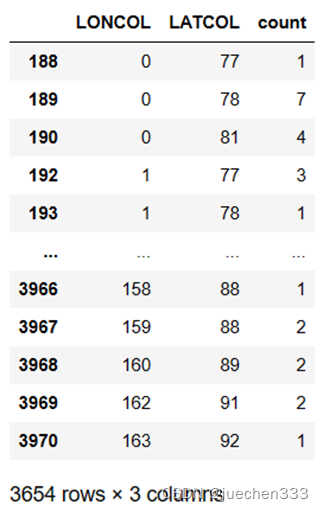

（3）统计结果与栅格地理信息的连接

前面已经完成了栅格数据量的统计，其中的LONCOL与LATCOL列标识了栅格编号，count则为数据量统计。接下来需要把统计把统计出的结果连接到栅格的空间地理信息grid_sz表上，也就是执行表的连接。

在对DataFrame和GeoDataFrame表连接的时候需要特别注意，merge函数保留传入的第一个对象的数据形式，如果想要让连接后的表格保持GeoDataFrame形式，则必须将地理信息表放在前面。

# 将栅格数据与统计数据进行表连接，在栅格数据上加上数据量
grid_count = pd.merge(grid_sz,data_distribution,on = ['LONCOL','LATCOL'])
grid_count

查看结果的类型

type(grid_count)

geopandas.geodataframe.GeoDataFrame

（4）栅格数据分布的可视化

指定栅格颜色随count列数值变化（即颜色映射），栅格的边界为0时，绘制出的效果即类似像素画。

# 绘制
import matplotlib.pyplot as plt
fig = plt.figure(1,(10,8),dpi = 250)
ax = plt.subplot(111)
# 绘制行政区划的边界
sz.plot(ax = ax, edgecolor = (0,0,0,1), facecolor = (0,0,0,0), linewidths = 0.5)
# 设置colormap与colorbar
import matplotlib as mpl
# 设置99%分位数为colorbar最大值
vmax = grid_count['count'].quantile(0.99)
# 换一种内置颜色
cmapname = 'plasma'
cmap = mpl.cm.get_cmap(cmapname)
# 创建colorbar的纸，命名为cax
cax = plt.axes([0.08, 0.4, 0.02, 0.3])
# 此时因为创建了新的纸，plt移动到了cax这张纸上，设定colorbar的标题
plt.title('count')
# plt移动回ax这张纸上
plt.sca(ax)
# 绘制栅格
grid_count.plot(ax = ax, column = 'count',linewidth = 0,    #指定颜色映射的列
               vmin = 0, vmax = vmax, cmap = cmap,          #设置colorbar与数值范围
               legend = True, cax = cax)                    #显示colorbar色条
plt.axis('off')
plt.xlim(113.6,114.8)
plt.ylim(22.4,22.9)
plt.show()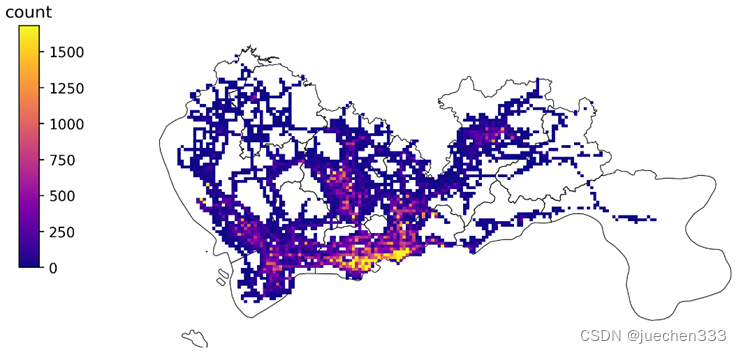

2.出租车GPS数据空间分布散点图

在绘制数据的分布情况时，还可以采用更精致的散点图进行绘制。与栅格统计的原理一样，散点也需要集计统计才能进行绘制。

# 经纬度保留三位小数
data2 = data[['Lng','Lat']].round(3).copy()
# 集计每个小范围内的数据量
data2['count'] = 1
data2 = data2.groupby(['Lng','Lat'])['count'].count().reset_index()
# 排序数据，让数据量小的放上面先画，数据量大的放下面后画
data2 = data2.sort_values(by = 'count')
data2

将上面统计的GPS点以散点图的形式绘制，同时给图表加上地图的底图与比例尺指北针。

# 创建图框
import seaborn as sns
import matplotlib as mpl  
import matplotlib.pyplot as plt  
import transbigdata as tbd 
fig = plt.figure(1,(8,8),dpi = 80)      
ax = plt.subplot(111)  
plt.sca(ax)      
# 绘制行政区划的边界
bounds = [113.7, 22.42, 114.3, 22.8]  
sz.plot(ax = ax,edgecolor = (0,0,0,0),facecolor = (0,0,0,0.1),linewidths=0.5)
# 定义colorbar  
pallete_name = "BuPu"  
colors = sns.color_palette(pallete_name, 3)  
colors.reverse()  
cmap = mpl.colors.LinearSegmentedColormap.from_list(pallete_name, colors)  
vmax = data2['count'].quantile(0.99)  
norm = mpl.colors.Normalize(vmin=0, vmax=vmax)  
# 绘制散点图 
plt.scatter(data2['Lng'],data2['Lat'],s = 1,alpha = 1,c = data2['count'],cmap = cmap,norm=norm )  
# 添加比例尺和指北针  
tbd.plotscale(ax,bounds = bounds,textsize = 10,compasssize = 1,accuracy = 2000,rect = [0.06,0.03])  
plt.axis('off')  
plt.xlim(bounds[0],bounds[2])  
plt.ylim(bounds[1],bounds[3])  
# 绘制colorbar    
cax = plt.axes([0.15, 0.33, 0.02, 0.3])  
plt.colorbar(cax=cax)  
plt.title('count')
plt.show()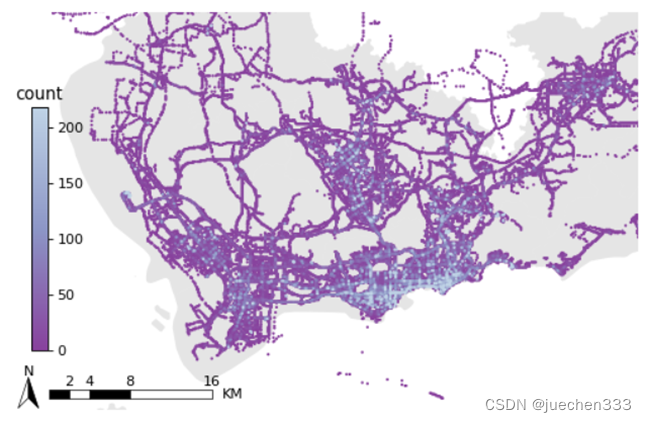

3.出租车GPS数据空间分布热力图

对数据的空间分布，还可以采用热力图进行绘制。在Matplotlib中绘制热力图则有两种方式，一种是采用等高线图直接对数据的分布进行绘制，另外一种则是用二维核密度绘制。

（1）等高线图plt.contour/plt.contourf

plt.contour（只绘制等高线）与plt.contourf（绘制等高线且在等高线之间填充颜色）是Matplotlib提供的等高线绘制方法，绘制出来的颜色代表的值代表数据量密度具有现实物理意义。

import numpy as np  
# 转换数据透视表，变成矩阵格式
d = data2.pivot(columns = 'Lng',index = 'Lat',values = 'count').fillna(0)  
#取对数，缩小最大最小值之间的差距
z = np.log(d.values)
x = d.columns  
y = d.index  
# 划分层数  
levels = np.linspace(0, z.max(), 25)

import matplotlib as mpl  
import matplotlib.pyplot as plt  
import transbigdata as tbd
fig = plt.figure(1,(8,8),dpi = 80)      
ax = plt.subplot(111)  
plt.sca(ax)  
# 调整整体空白
fig.tight_layout(rect = (0.05,0.1,1,0.9))
# 绘制行政区划的边界
bounds = [113.7, 22.42, 114.3, 22.8]  
sz.plot(ax = ax,edgecolor = (0,0,0,0),facecolor = (0,0,0,0.1),linewidths=0.5)
# 定义colorbar  
import matplotlib
cmap = matplotlib.colors.LinearSegmentedColormap.from_list('cmap', ['#9DCC42','#FFFE03','#F7941D','#E9420E','#FF0000'], 256)
# 绘制等高线图  
plt.contourf(x,y,z, levels=levels, cmap=cmap,origin = 'lower') 
# 添加比例尺和指北针    
tbd.plotscale(ax,bounds = bounds,textsize = 10,compasssize = 1,accuracy = 2000,rect = [0.06,0.03])    
plt.axis('off')  
plt.xlim(bounds[0],bounds[2])  
plt.ylim(bounds[1],bounds[3])    
# 绘制colorbar  
cax = plt.axes([0.13, 0.32, 0.02, 0.3])  
cbar = plt.colorbar(cax=cax)  
# 调整colorbar的显示标记位置
val = [1,10,100,1000,5000]
pos = np.log(np.array(val))
# 在什么位置显示标记
cbar.set_ticks(pos)
# 标记显示什么内容
cbar.set_ticklabels(val)
plt.title('Count')
plt.show()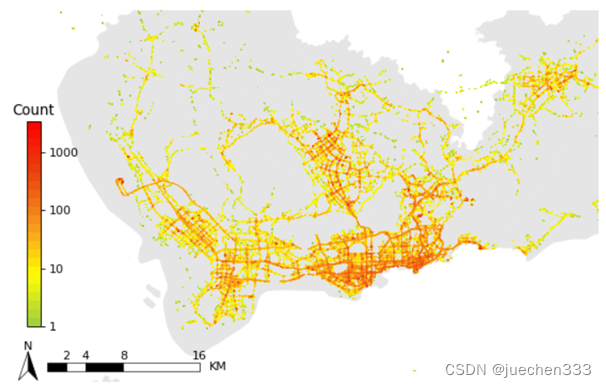  

（2）空间核密度seaborn-kdeplot

赋予每一个点数据一定的影响范围，利用离散的数据估计连续概率密度，将数据的分布进行平滑处理。经过处理后，估计出来的是抽象的密度值，无法对应现实的物理意义。

# 导入绘图包
import matplotlib as mpl
import matplotlib.pyplot as plt
import transbigdata as tbd
import seaborn as sns
import numpy as np
fig = plt.figure(1,(10,10),dpi = 60)    
ax = plt.subplot(111)
plt.sca(ax)
# 调整整体空白
fig.tight_layout(rect = (0.05,0.1,1,0.9))
# 绘制行政区划的边界
bounds = [113.7, 22.42, 114.3, 22.8]  
sz.plot(ax = ax,edgecolor = (0,0,0,0),facecolor = (0,0,0,0.1),linewidths=0.5)
# colorbar的数据
cmap = mpl.colors.LinearSegmentedColormap.from_list('cmap', ['#9DCC42','#FFFE03','#F7941D','#E9420E','#FF0000'], 256)
# 设定位置
plt.axis('off')
plt.xlim(bounds[0],bounds[2])
plt.ylim(bounds[1],bounds[3])
# 定义colorbar位置
cax = plt.axes([0.13, 0.32, 0.02, 0.3])
# 绘制二维核密度图
sns.kdeplot('Lng','Lat',                     #指定x与y坐标所在的列
            data = data2[data2['count']>10], #传入数据，筛选去除太小的值
            weights = 'count',               #设定权重所在字段
            alpha = 0.8,                     #透明度
            gridsize = 120,                  #绘图精细度，越高越慢
            bw = 0.03,                    #高斯核大小（经纬度），越小越精细
            cmap = cmap,                     #定义colormap
            ax = ax,                         #指定绘图位置
            shade = True,                    #等高线间是否填充颜色
            shade_lowest = False,            #最底层不显示颜色
            cbar = True,                     #显示colorbar
            cbar_ax = cax                    #指定colorbar位置
           )
plt.show()

（三）、出租车订单出行特征分析

1.出租车订单出行特征提取

（1）出行OD提取的代码实现

提取出行的开始和结束信息。

# 导入pandas包，并赋值给变量pd
import pandas as pd
# 读取GPS数据文件
data = pd.read_csv('D:/Project/Jupyter_Project/Data/data/TaxiData-clean.csv')
# 构建StatusChange列
data['StatusChange'] = data['OpenStatus'] - data['OpenStatus'].shift()
# 筛选出行开始和结束信息  
oddata = data[((data['StatusChange'] == -1)|
               (data['StatusChange'] == 1))&
               (data['VehicleNum'].shift() == data['VehicleNum'])]
# 删去无用的列
oddata = oddata.drop(['OpenStatus','Speed'],axis = 1)
oddata

数据处理成oddata的形式，虽然能够从数据中找到订单的OD，但是每个订单有两条数据，这行数据能同时包含订单的OD信息、订单开始和结束信息，利用shfit函数处理连续数据，但要注意使用shift后要保证数据属于同一辆出租车。

# 首先给oddata更改列名  
oddata.columns = ['VehicleNum', 'Stime', 'SLng', 'SLat', 'StatusChange']  
# 把一个订单的两行数据整理成一行  
oddata['Etime'] = oddata['Stime'].shift(-1)  
oddata['ELng'] = oddata['SLng'].shift(-1)  
oddata['ELat'] = oddata['SLat'].shift(-1)  
# 筛选正确的订单OD数据：StatusChange == 1；shift后的数据属于同一个出租车  
oddata = oddata[(oddata['StatusChange'] == 1)&  
                  (oddata['VehicleNum'] == oddata['VehicleNum'].shift(-1))]  
# 去掉StatusChange列
oddata = oddata.drop('StatusChange',axis = 1)  
oddata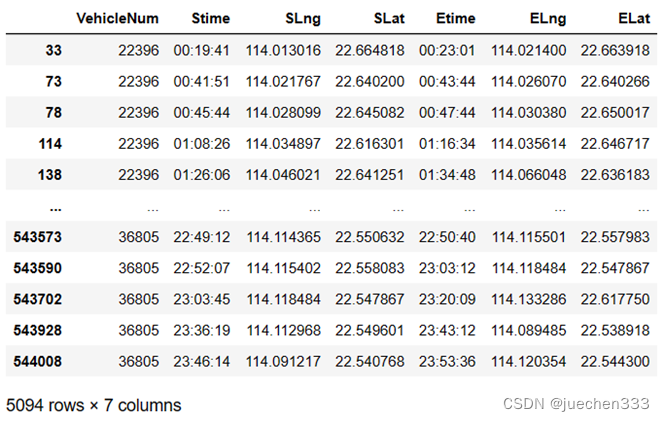

（2）出行订单数量的时间分布

统计oddata数据表，得到出行订单数量的时间分布。

# 统计每小时订单数
oddata['Hour'] = oddata.apply(lambda r:r['Stime'][:2],axis = 1).astype(int) 
Hourcount_od = oddata.groupby('Hour')['VehicleNum'].count()
Hourcount_od = Hourcount_od.rename('count').reset_index()
# 绘制折线图
import matplotlib.pyplot as plt
fig = plt.figure(1,(8,4),dpi = 300)
ax = plt.subplot(111)
plt.plot(Hourcount_od['Hour'],Hourcount_od['count'],'k-')
plt.plot(Hourcount_od['Hour'],Hourcount_od['count'],'k.')
plt.bar(Hourcount_od['Hour'],Hourcount_od['count'])
plt.ylabel('Trips')
plt.xlabel('Hour')
plt.xticks(range(24),range(24))
plt.title('Hourly trip count')
plt.ylim(0,350)
plt.show()

2.出租车出行订单持续时间的统计

（1）订单持续时间的统计

①标准化时间

标准化时间以0点为初始时间，将某一时刻转换为相对初始时间的时间差。

# 1.标准化时间
# 订单开始时间标准化
oddata['Stime_st'] = oddata['Stime'].apply(lambda r: int(r.split(':')[0]))*3600+oddata['Stime'].apply(lambda r: int(r.split(':')[1]))*60+oddata['Stime'].apply(lambda r: int(r.split(':')[2]))
# 订单结束时间标准化
oddata['Etime_st'] = oddata['Etime'].apply(lambda r: int(r.split(':')[0]))*3600+oddata['Etime'].apply(lambda r: int(r.split(':')[1]))*60+oddata['Etime'].apply(lambda r: int(r.split(':')[2]))    
# 计算时间差
oddata['duration'] = (oddata['Etime_st'] - oddata['Stime_st'])
oddata

②时间格式转换

将Stime和Etime转换为时间格式后进行差值计算。

# 2.时间格式转换
oddata['duration'] = pd.to_datetime(oddata['Etime']) - pd.to_datetime(oddata['Stime'])    
# 将时间差转换为秒
oddata['duration'] = oddata['duration'].apply(lambda r: r.seconds)
oddata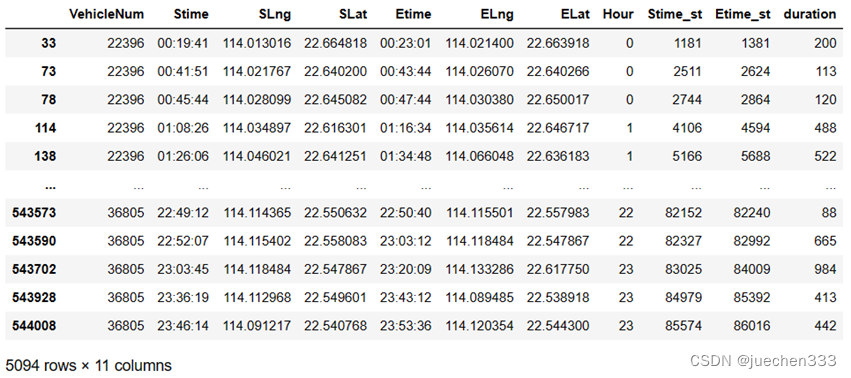

（2）订单持续时间的箱形图绘制

Matplotlib中箱型图的绘制有两种方法：Matplotlib的boxplot函数和seaborn库的boxplot。

首先用Matplotlib的boxplot函数进行绘制。

# 订单持续时间箱型图的绘制：plt.boxplot
import matplotlib.pyplot as plt
fig = plt.figure(1,(6,4),dpi = 250)
ax = plt.subplot(111)  
plt.sca(ax)  
# 整理箱型图的数据，循环遍历每个小时，将列数据放入datas变量中
datas = []
for hour in range(24):
    datas.append(oddata[oddata['Hour']==hour]['duration']/60)
# 绘制箱型图  
plt.boxplot(datas)  
# 更改x轴ticks的文字,传入两个参数，第一个为位置，第二个为标注文字
plt.xticks(range(1,25),range(24))
plt.ylabel('Order time(minutes)')
plt.xlabel('Order start time')
plt.ylim(0,60)
plt.show()

用seaborn库中的boxplot函数绘制。

# 订单持续时间箱型图的绘制：sns.boxplot
import matplotlib.pyplot as plt  
import seaborn as sns
fig = plt.figure(1,(6,4),dpi = 250)
ax = plt.subplot(111)
plt.sca(ax)
# 只需要一行，指定传入的数据，x轴y轴分别是哪个维度
sns.boxplot(x="Hour", y=oddata["duration"]/60, data=oddata,ax = ax)
plt.ylabel('Order time(minutes)')
plt.xlabel('Order start time')
plt.ylim(0,60)
plt.show()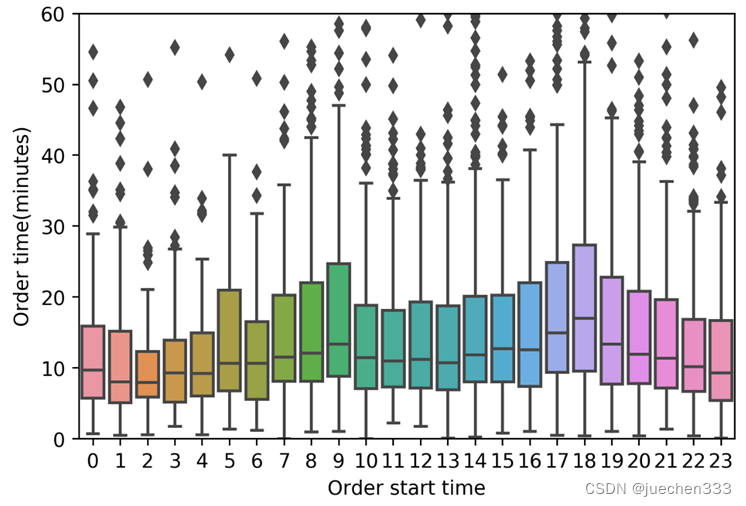

3.出租车出行订单的栅格OD可视化

（1）出行订单数据的栅格对应

将出行订单OD数据与栅格对应

# 计算起点对应的栅格经纬度编号
oddata['SLONCOL'] = ((oddata['SLng'] - (lonStart - deltaLon / 2))/deltaLon).astype('int')
oddata['SLATCOL'] = ((oddata['SLat'] - (latStart - deltaLat / 2))/deltaLat).astype('int')   
# 计算终点对应的栅格经纬度编号
oddata['ELONCOL'] = ((oddata['ELng'] - (lonStart - deltaLon / 2))/deltaLon).astype('int')
oddata['ELATCOL'] = ((oddata['ELat'] - (latStart - deltaLat / 2))/deltaLat).astype('int')
# 剔除起终点在一个栅格内的记录
oddata = oddata[-((oddata['SLONCOL']==oddata['ELONCOL'])&
                  (oddata['SLATCOL']==oddata['ELATCOL']))]
# 剔除不在研究范围内的OD记录
oddata = oddata[(oddata['SLONCOL']>=0)&(oddata['SLATCOL']>=0)&
                (oddata['ELONCOL']>=0)&(oddata['ELATCOL']>=0)&
                (oddata['SLONCOL']<=lonsnum)&
                (oddata['SLATCOL']<=latsnum)&
                (oddata['ELONCOL']<=lonsnum)&
                (oddata['ELATCOL']<=latsnum)]   
# 列数比较多，转置方便查看
oddata.iloc[:5].T

（2）栅格OD集计与起终点坐标计算

通过groupby函数以起终点栅格编号列为依据集计订单数量，并计算起终点对应栅格中心点经纬度坐标。

#对以起终点栅格编号列为依据集计订单数量
OD = oddata.groupby(['SLONCOL','SLATCOL','ELONCOL','ELATCOL'])['VehicleNum'].count().rename('count').reset_index()
#起点栅格中心点经纬度
OD['SHBLON'] = OD['SLONCOL'] * deltaLon + (lonStart - deltaLon / 2)
OD['SHBLAT'] = OD['SLATCOL'] * deltaLat + (latStart - deltaLat / 2)
#终点栅格中心点经纬度    
OD['EHBLON'] = OD['ELONCOL'] * deltaLon + (lonStart - deltaLon / 2)
OD['EHBLAT'] = OD['ELATCOL'] * deltaLat + (latStart - deltaLat / 2)
#排序，将count值大的OD排在最下  
OD = OD.sort_values(by = 'count')
OD

（3）对上面统计的出行OD进行可视化绘制，可以用Matplotlib的折线绘制和GeoPandas的LineString绘制方法。

①Matplotlib的折线

#绘制OD
import matplotlib.pyplot as plt
fig = plt.figure(1,(10,8),dpi = 250)
ax  = plt.subplot(111)
plt.sca(ax)

#绘制地图底图，设置两者均在ax上绘制
grid_sz.plot(ax =ax,edgecolor = (0,0,0,0.8),facecolor = (0,0,0,0),linewidths=0.2)
sz.plot(ax = ax,edgecolor = (0,0,0,1),facecolor = (0,0,0,0),linewidths=0.5)

#设置colormap的数据
import matplotlib
vmax = OD['count'].max()
#设定一个标准化的工具，设定OD的colormap最大最小值，他的作用是norm(count)就会将count标准化到0-1的范围内
norm = matplotlib.colors.Normalize(vmin=0,vmax=vmax)
#设定colormap的颜色
cmapname = 'autumn_r'
#cmap是一个获取颜色的工具，cmap(a)会返回颜色，其中a是0-1之间的值
cmap = matplotlib.cm.get_cmap(cmapname)

#遍历绘制OD
for i in range(len(OD)):
    r = OD.iloc[i]
    count = r['count']
    linewidth = 1.5*(count/OD['count'].max())

plt.plot([r['SHBLON'],r['EHBLON']],[r['SHBLAT'],r['EHBLAT']],linewidth = linewidth,color = cmap(norm(count)))

#隐藏坐标轴
plt.axis('off')
plt.show()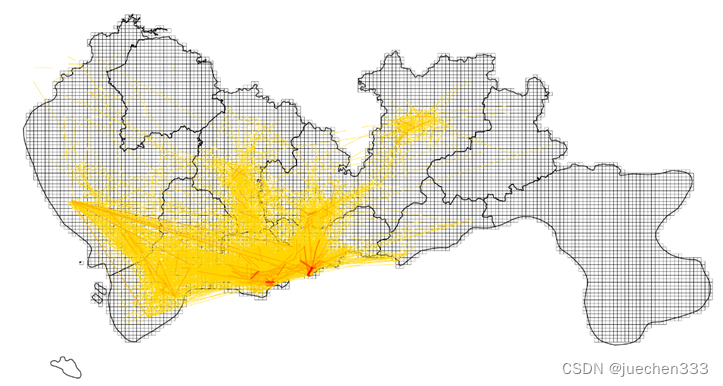

②GeoPandas的LineString方法

from shapely.geometry import LineString
# 遍历生成OD的LineString对象，并赋值给geometry列
OD['geometry'] = OD.apply(lambda r:LineString([[r['SHBLON'],r['SHBLAT']],[r['EHBLON'],r['EHBLAT']]]),axis = 1)
# 转换为GeoDataFrame
OD = gpd.GeoDataFrame(OD)
# 绘制看看是否能够识别图形信息
OD.plot()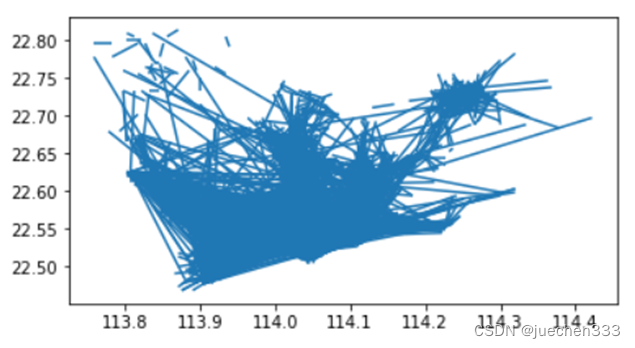

生成GeoDataFrame后，用plot函数绘制，并指定颜色映射的列，即可绘制OD。

# 绘制
# 创建图框
import matplotlib.pyplot as plt
fig = plt.figure(1,(10,8),dpi = 250)
ax = plt.subplot(111)
# 绘制栅格与行政区划边界
grid_sz.plot(ax = ax,edgecolor = (0,0,0,0.8),facecolor = (0,0,0,0),linewidths=0.2)
sz.plot(ax = ax,edgecolor = (0,0,0,1),facecolor = (0,0,0,0),linewidths=0.5)
# 设置colormap的数据
import matplotlib as mpl
vmax = OD['count'].max()
cmapname = 'autumn_r'
cmap = mpl.cm.get_cmap(cmapname)
# 创建colorbar的纸，命名为cax
cax = plt.axes([0.08, 0.4, 0.02, 0.3])
plt.title('count')
plt.sca(ax)
# 绘制OD
OD.plot(ax = ax,column = 'count',                       #指定在ax上绘制，并指定颜色映射的列
        linewidth = 1.5*(OD['count']/OD['count'].max()),#指定线宽
        cmap = cmap,vmin = 0,vmax = vmax,               #设置OD的颜色
        legend=True,cax = cax)                          #设置绘制色标
# 隐藏边框，并设定显示范围
plt.axis('off')
plt.xlim(113.6,114.8)
plt.ylim(22.4,22.9)
# 显示图
plt.show()

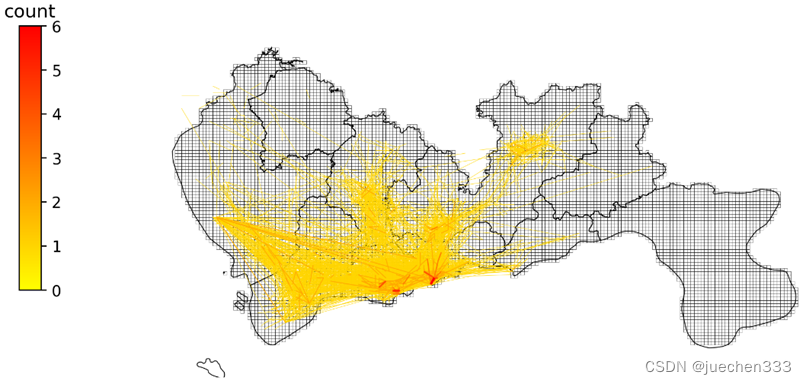
4.出租车出行的OD期望线绘制

（1）栅格匹配至行政规划

在栅格匹配至行政规划时，首先提取栅格的中心点，将栅格地理信息由矢量面转变为点。再使用GeoPandas的sjoin函数进行空间对象的空间连接，其用法与Pandas的merge表连接非常相似。

# 读取行政区划的矢量图形
sz = gpd.GeoDataFrame.from_file(r'D:\Project\Jupyter_Project\Data\data\sz\sz.shp',encoding = 'utf8')
# 读取栅格数据
grid_sz = gpd.GeoDataFrame.from_file('D:\Project\Jupyter_Project\Data\data\grid_sz.json')
# 提取栅格中心点，创建一个新变量
grid_centroid = grid_sz.copy()
# 提取栅格中心点，赋值给grid_centriod的geometry
grid_centroid['geometry'] = grid_centroid.centroid
# 栅格匹配到行政区划：gpd.sjoin
grid_centroid = gpd.sjoin(grid_centroid,sz)
grid_centroid

（2）数据匹配到行政区划

将栅格信息与OD进行表连接，获得出行起终点所在的行政区划信息。

# 保留有用的字段  
grid_centroid = grid_centroid[['LONCOL','LATCOL','qh']]
# 改变grid_centroid字段名，使其与OD数据起点栅格编号列能够匹配
grid_centroid.columns = ['SLONCOL','SLATCOL','Sqh']
OD = pd.merge(OD,grid_centroid,on = ['SLONCOL','SLATCOL'] )
# 改变grid_centroid字段名，使其与OD数据终点栅格编号列能够匹配
grid_centroid.columns = ['ELONCOL','ELATCOL','Eqh']
OD = pd.merge(OD,grid_centroid,on = ['ELONCOL','ELATCOL'] )
# 集计OD量
qhod  = OD.groupby(['Sqh','Eqh'])['count'].sum().reset_index()
# 去除起终点在同个行政区划的数据
qhod = qhod[qhod['Sqh'] != qhod['Eqh']] 
qhod.head(5)

（3）行政区划间OD期望线绘制

将行政区划的中心点坐标与行政区划OD出行量进行表连接，将起终点经纬度对应至OD期望线上，转换为GeoDataFrame并为每一条OD生成LineString线型，使其成为地理信息数据。

# 匹配起点行政区划的中心点经纬度
tmp = sz[['centroid_x','centroid_y','qh']]
tmp.columns = ['S_x','S_y','Sqh']
qhod = pd.merge(qhod,tmp,on = 'Sqh')
# 匹配终点行政区划的中心点经纬度
tmp.columns = ['E_x','E_y','Eqh']
qhod = pd.merge(qhod,tmp,on = 'Eqh')
# 为OD期望线生成GeoDataFrame
qhod = gpd.GeoDataFrame(qhod)
qhod['geometry'] = qhod.apply(lambda r:LineString([[r['S_x'],r['S_y']],[r['E_x'],r['E_y']]]),axis = 1)
qhod.plot()

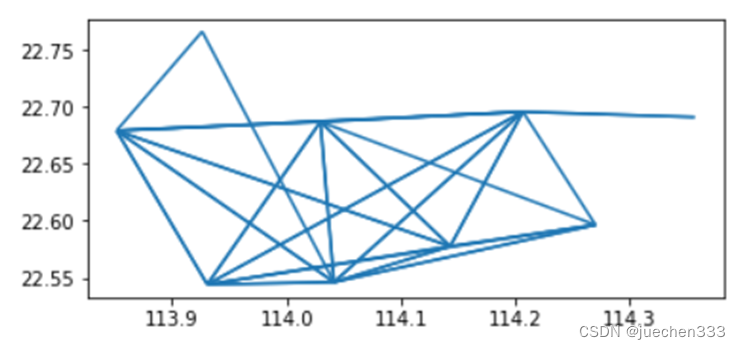
接下来对OD期望线进行可视化

# 绘制
# 创建图框  
import matplotlib.pyplot as plt  
fig = plt.figure(1,(10,8),dpi = 250)      
ax = plt.subplot(111)  
# 绘制行政区划边界  
sz.plot(ax = ax,edgecolor = (0,0,0,0),facecolor = (0,0,0,0.2),linewidths=0.5)
# 设置colormap的数据  
import matplotlib as mpl  
vmax = qhod['count'].max()  
cmapname = 'autumn_r'  
cmap = mpl.cm.get_cmap(cmapname)  
# 创建colorbar
cax = plt.axes([0.08, 0.4, 0.02, 0.3])  
plt.title('count')  
plt.sca(ax)  
# 绘制OD  
qhod.plot(ax = ax,column = 'count', #指定在ax上绘制，并指定颜色映射的列
        linewidth = 5*(qhod['count']/qhod['count'].max()),#指定线宽
        cmap = cmap,vmin = 0,vmax = vmax    #设置OD的颜色
        legend=True,cax = cax)           #设置绘制色标
# 隐藏边框，并设定显示范围
plt.axis('off')
plt.xlim(113.6,114.8)
plt.ylim(22.4,22.9)
# 显示图
plt.show()

六、实验结果

（一）、出租车数据的时间完整性评估

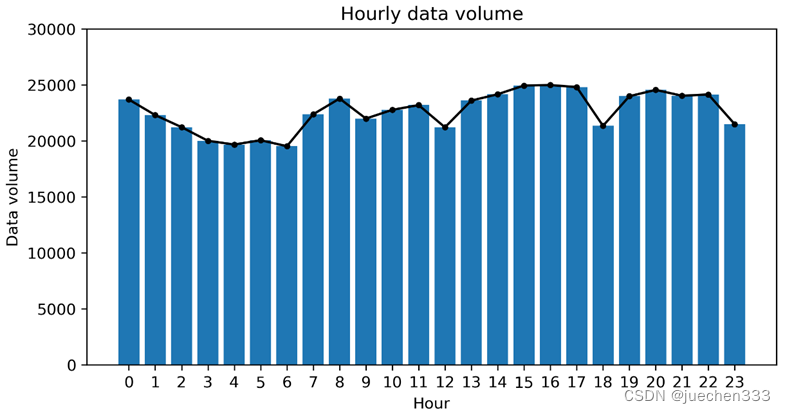
图1.小时数据量折线图

从数据量的时变折线图可以看出，数据在小时分布上并没有明显的数据缺失情况。

（二）、出租车数据的空间完整性评估

图2.GPS数据的空间分布（栅格集计）

图3.出租车GPS数据的空间分布散点图

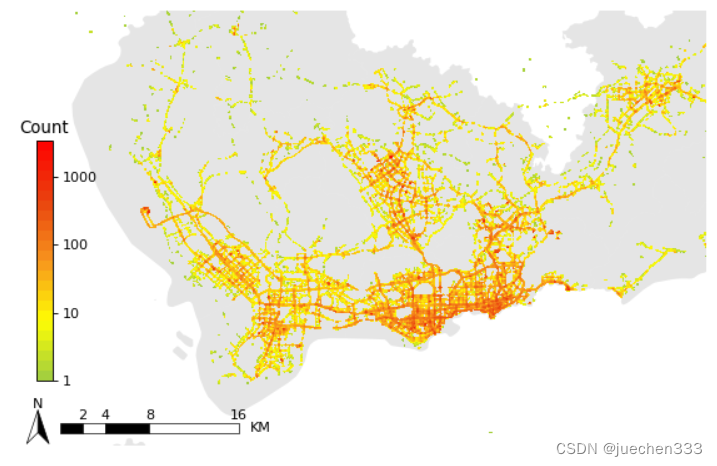
图4.数据分布的等高线图

图5.数据分布的空间二维核密度分布图

从图2-图5来看，数据集中分布于中心城区，郊区存在大片空白没数据的地方，这部分地方没有出租车需求。郊区有数据的地方则明显呈现线性分布，与道路的分布较为吻合。

（三）、出租车订单出行特征分析

图6.订单数量的小时分布

从订单的开始时间统计可以看出，出租车订单并没有在某个时间段存在明显缺失。在夜间时段，订单数量会有一个明显的低谷，这也与实际的需求相符。从数据量与订单量的时间分布上看，出租车数据在时间分布上是较为完整的。

图7.plt.boxplot绘制的分组箱型图

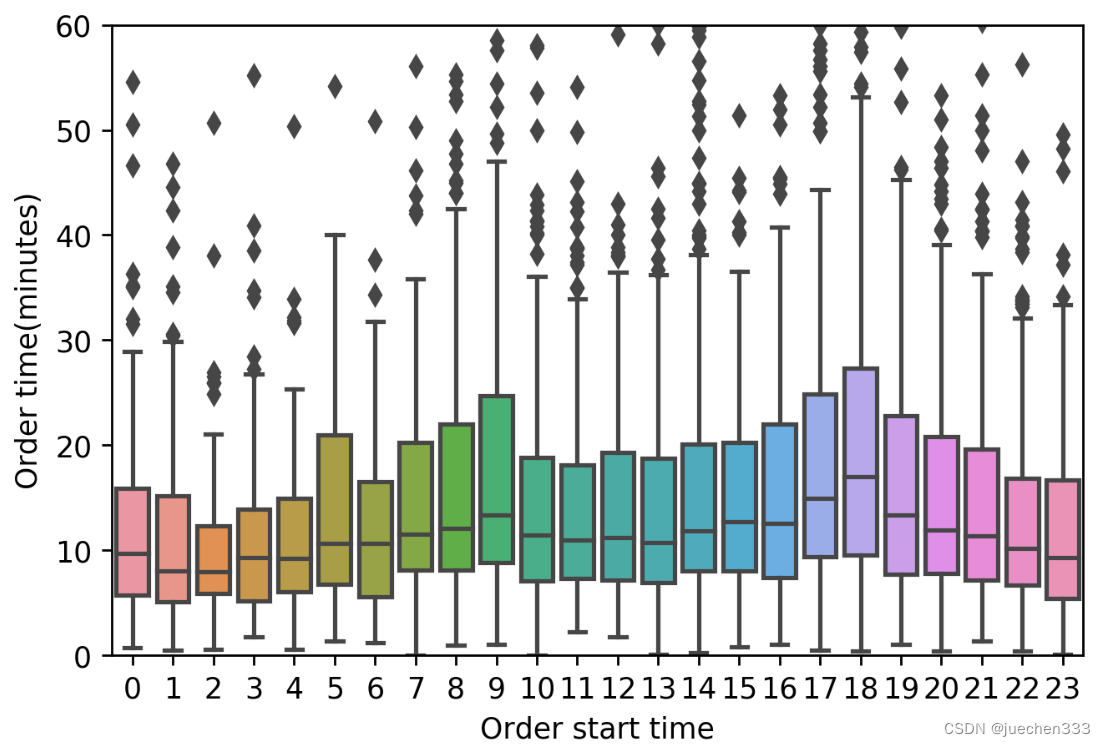
图8.sns.boxplot绘制的分组箱型图

经过前面的数据处理，成功地计算出了出租车出行订单的持续时间，并用箱型图展示了不同时间段订单持续时间的分布情况。从中可以看出，出租车的订单持续时间在一日之中的不同时间内存在一定差异，在早晚高峰时间，订单的持续时间明显更长，因为高峰时间城市道路更加拥挤，出行所需的时间当然就更长了。

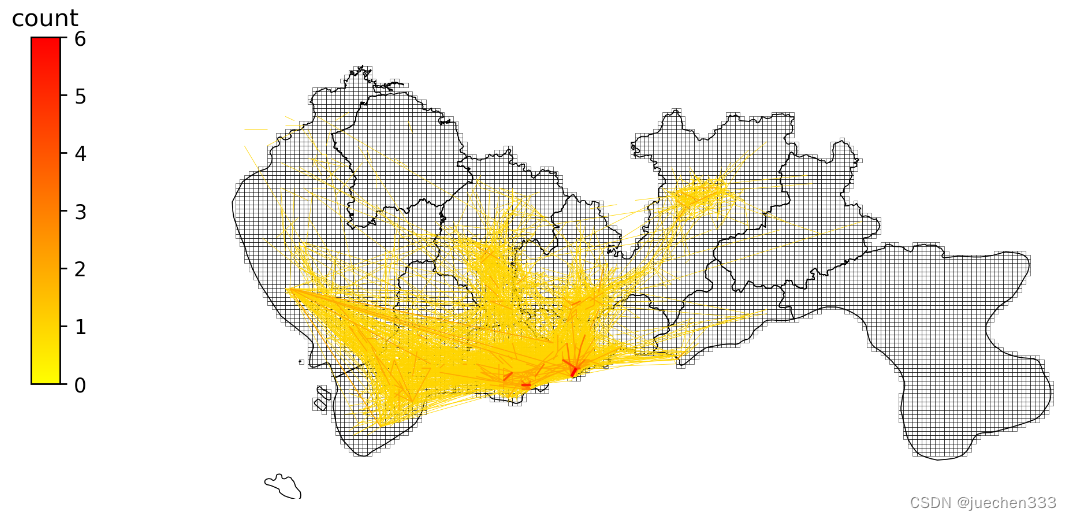
图9.OD绘制结果

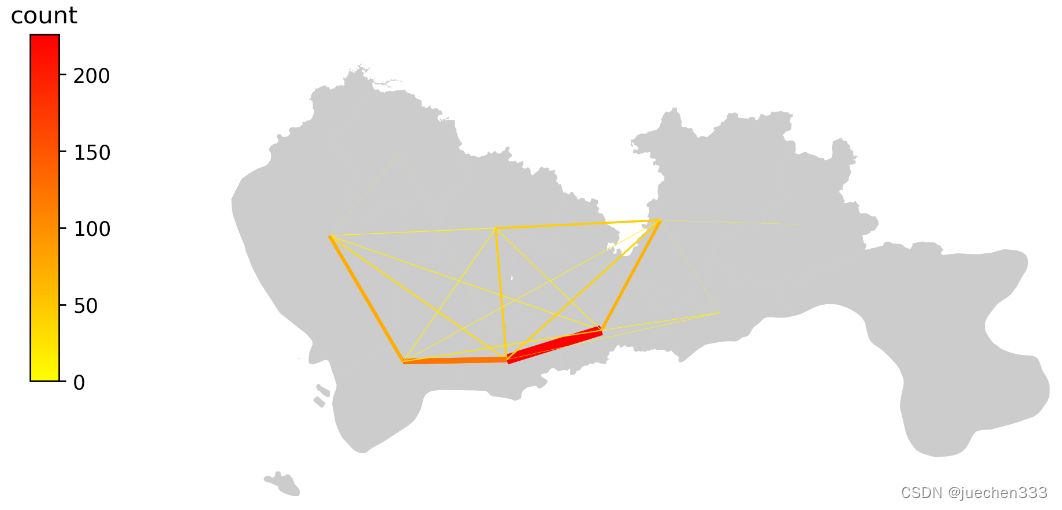
图10.OD期望线绘制

从出行订单OD数据的空间分布上看，数据的出行订单集中分布于城市的核心区域，也与真实的需求相符合。