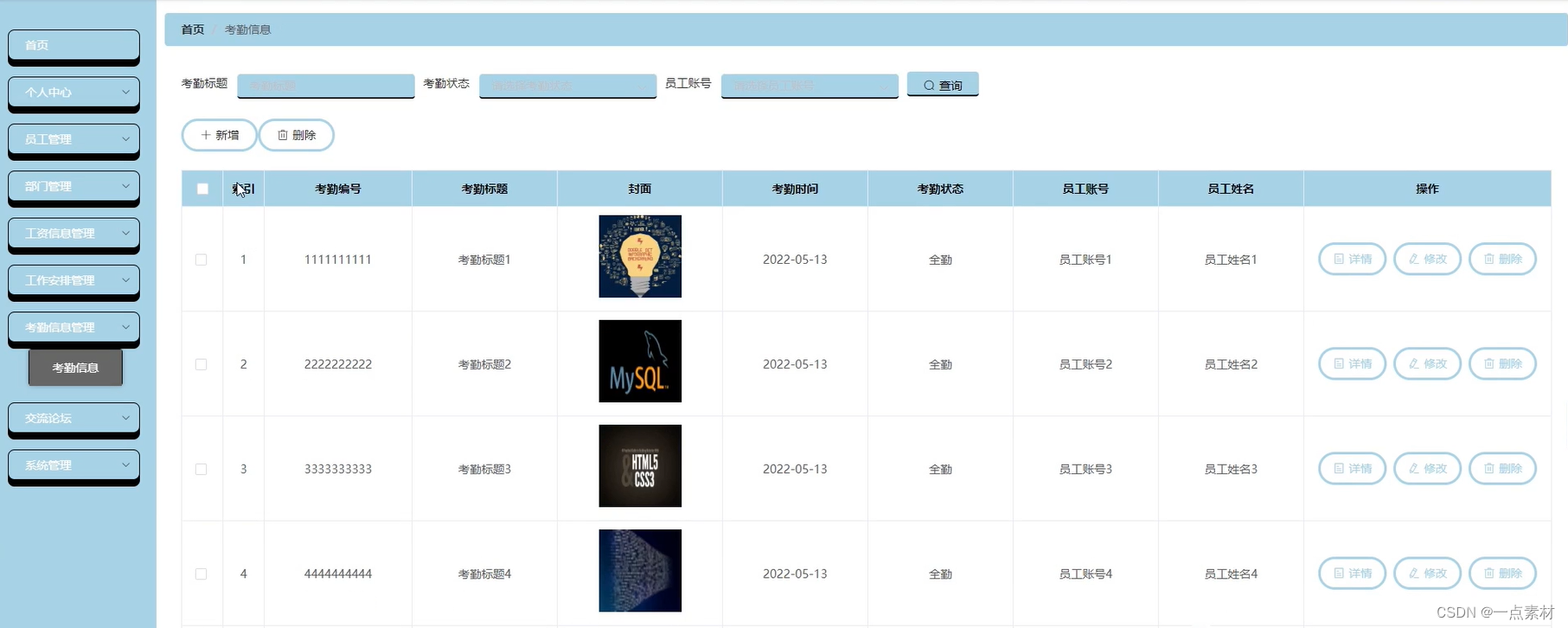
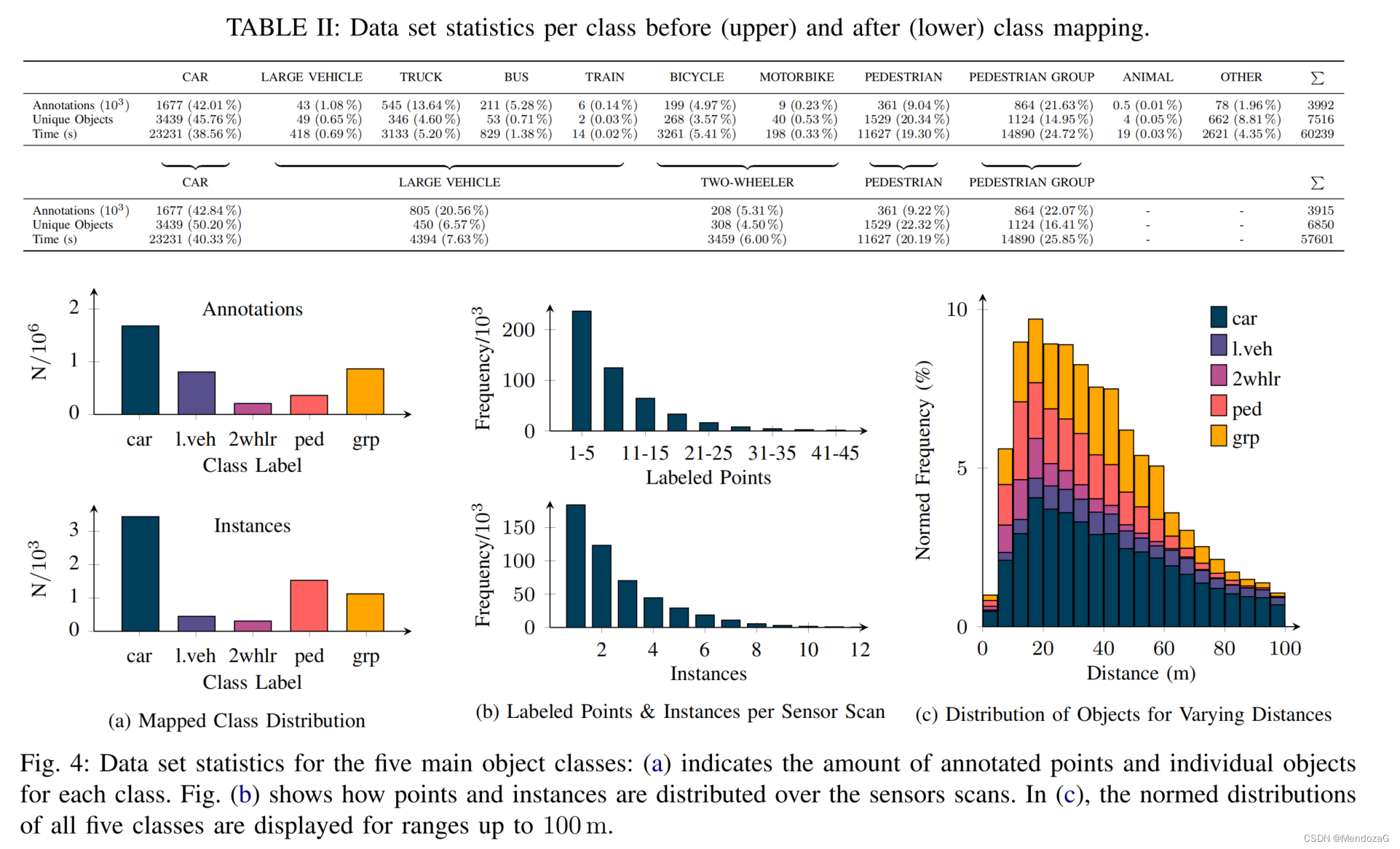
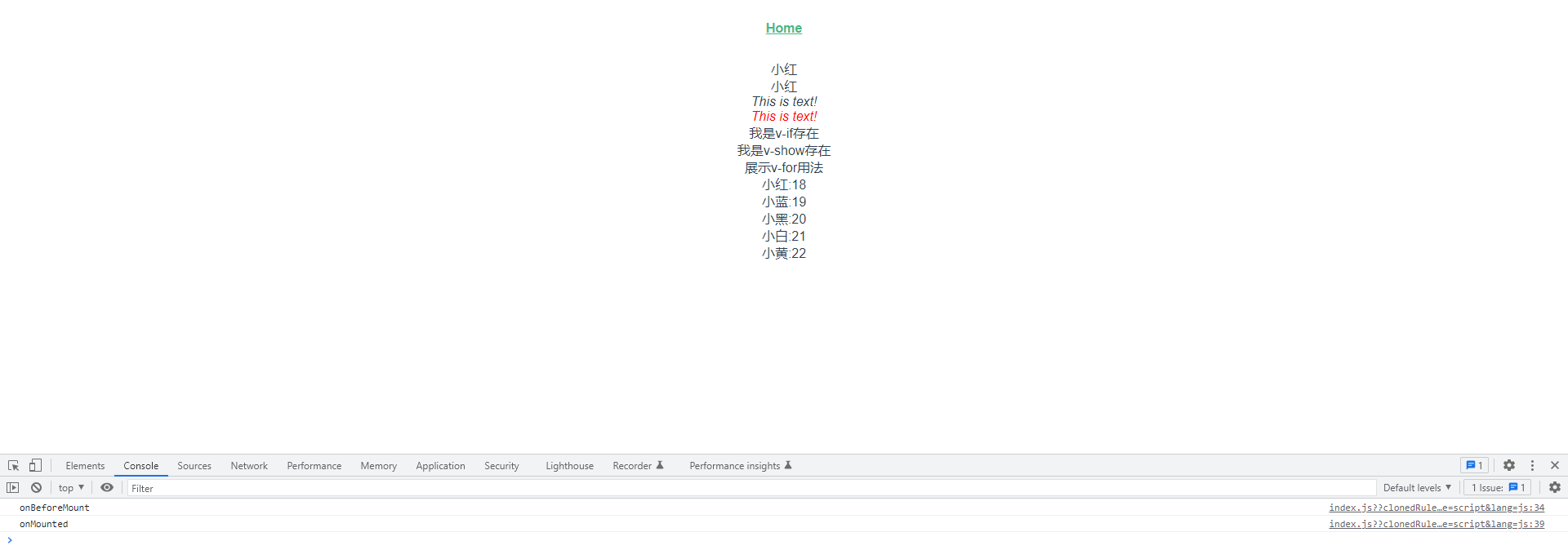
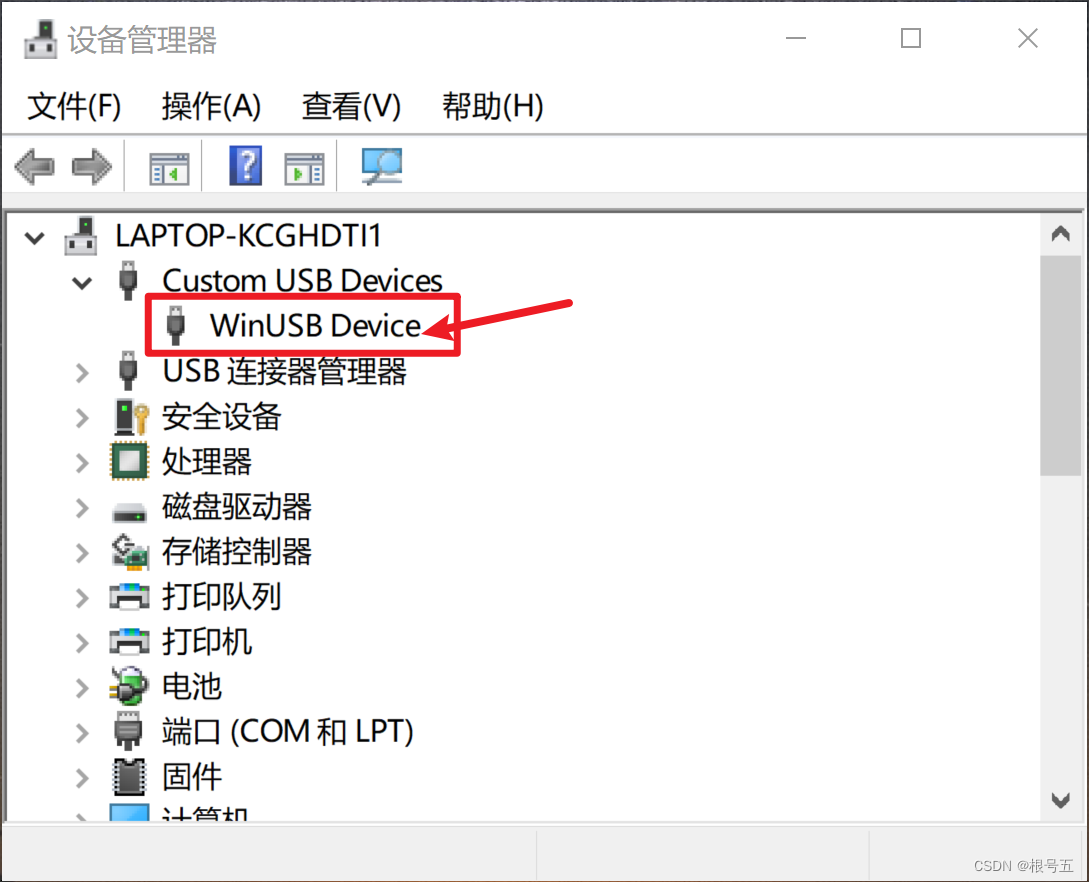
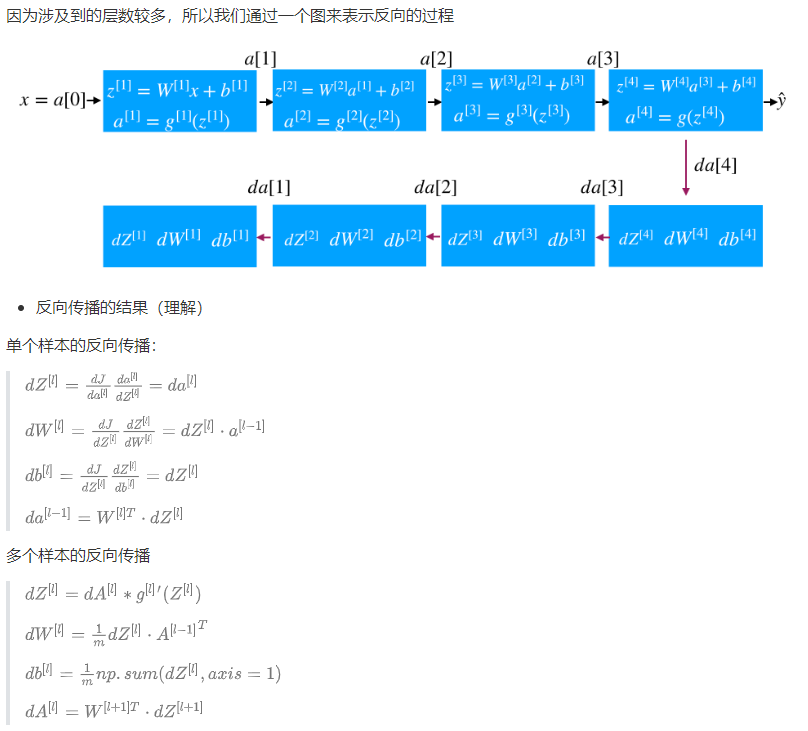
概述

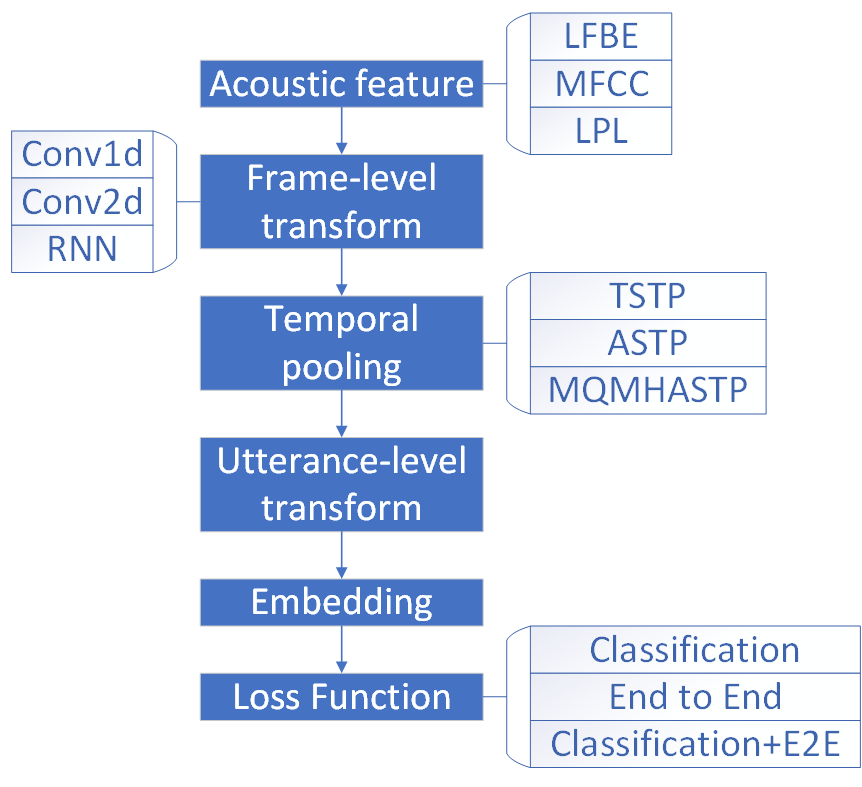
• Temporal pooling（时序池化）是说话人识别神经网络中，声学特征经过frame-level变换之后，紧接着会进入的一个layer。目的是将维度为$(bs,F,T)$的特征图，变换成维度为$(bs,F)$的特征向量
  

• 在这个过程中，T这个维度，也就是frame的个数，消失了，因此时序池化本质上可以看作：从一系列frame的特征中，挖掘出最能代表特征图信息的特征，并且要把长度可变的frame序列，变换为固定长度的特征向量

• 时序池化的本质决定了Attention机制在其中的重要性，因为不同frame的重要性是不同的，不同frame的不同特征的重要性也是不同的，对整个特征图的每一个值都计算Attention分数（关于Attention分数，可参考深入理解Self-attention（自注意力机制）），然后利用Attention分数加权计算统计量（如均值、标准差），最后串联起来作为输出，成为一种重要的方法

• 本文将介绍说话人识别中，效果较好的时序池化方法，持续更新

ASTP

• ASTP（Attentive Statistics Pooling）是2018提出的，至今仍然广为使用的带有Attention的时序池化层
  

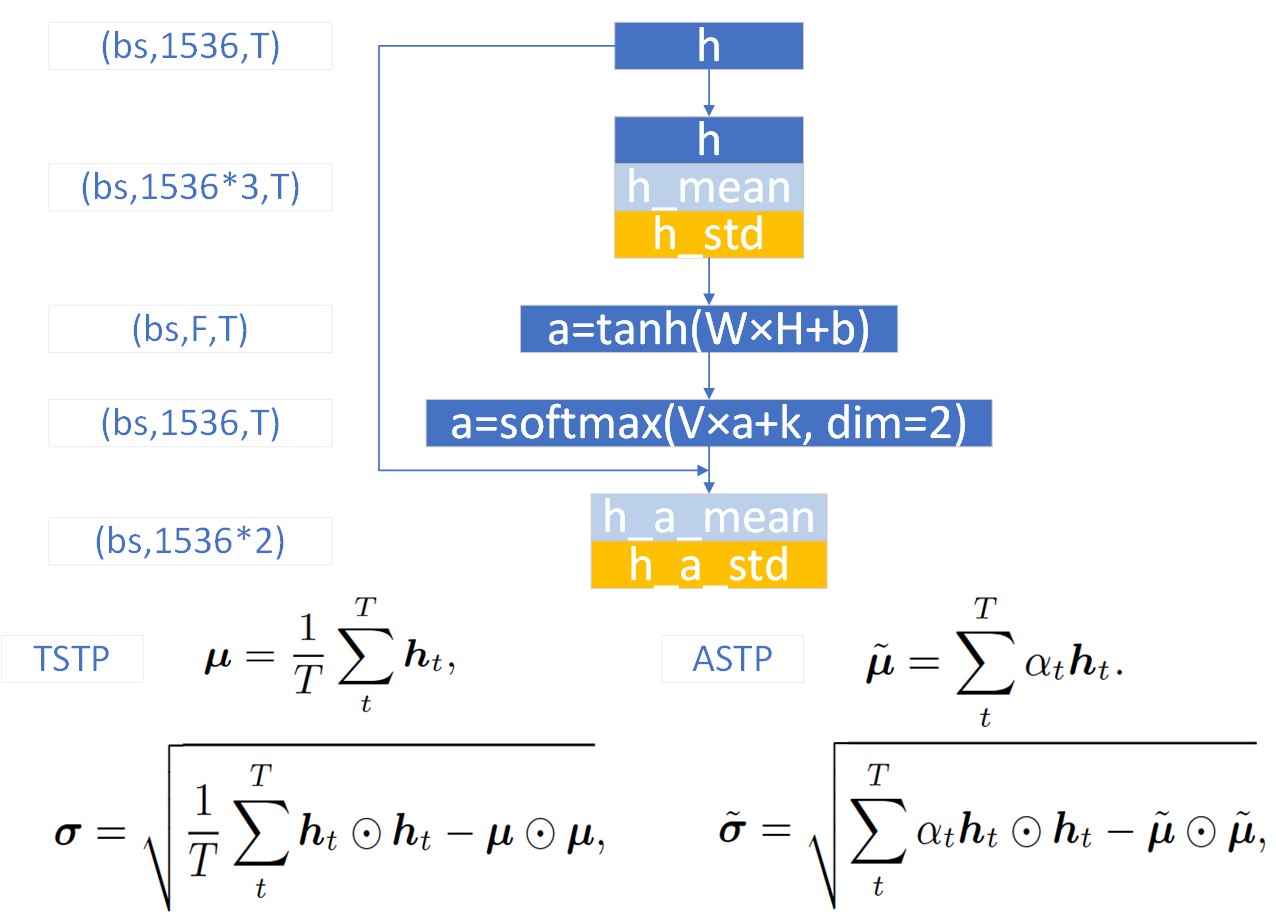
• 假设输入特征图维度为$(bs,1536,T)$，记为h，按照T维度计算每个特征维度的均值和标准差，如上图的TSTP公式所示（符号$\odot$表示哈达玛积，即对应项相乘，两个因子的维度必须相同，从而结果的维度与因子的维度也相同），从而T维度消失，得到的均值和标准差维度均为$(bs,1536)$

• TSTP公式，将每个frame的重要性视为等同的，然后计算均值和标准差，这是Attention机制出现前，常用的时序池化方法

• 之后的操作很神奇，将均值在T维度重复堆叠T次，维度恢复为$(bs,1536,T)$，对标准差也是堆叠，维度恢复为$(bs,1536,T)$，接着将特征图、均值和标准差在特征维度进行串联，得到的特征图维度为$(bs,1536\ast 3,T)$，记为H

• 对H进行1维卷积，等价于上图的$W\times H+b$（PyTorch1维卷积默认对每个out-channel带有一个bias），目的是将每个frame的特征从1536*3维降维映射到F维，F可取128，然后经过tanh激活函数（如果使用ReLU，会导致网络难以收敛），得到特征图a，维度为$(bs,F,T)$

• 对a进行1维卷积，等价于上图的$V\times a+k$，目的是将每个frame的特征从F维恢复映射到与h相同的维度，即1536，然后在T维度，进行softmax激活，得到特征图a，维度为$(bs,1536,T)$

• 此时的特征图a的每一行特征，在T维度上求和，都等于1，这是softmax激活的效果，又因为与h的维度相同，所以可以将a视为一种Attention分数，利用上图的ASTP公式，对h求基于Attention的均值和标准差

• 基于Attention的均值和标准差，维度都为$(bs,1536)$，再将它们按照特征维度进行串联，得到ASTP最终的输出，维度为$(bs,1536\ast 2)$

MQMHASTP

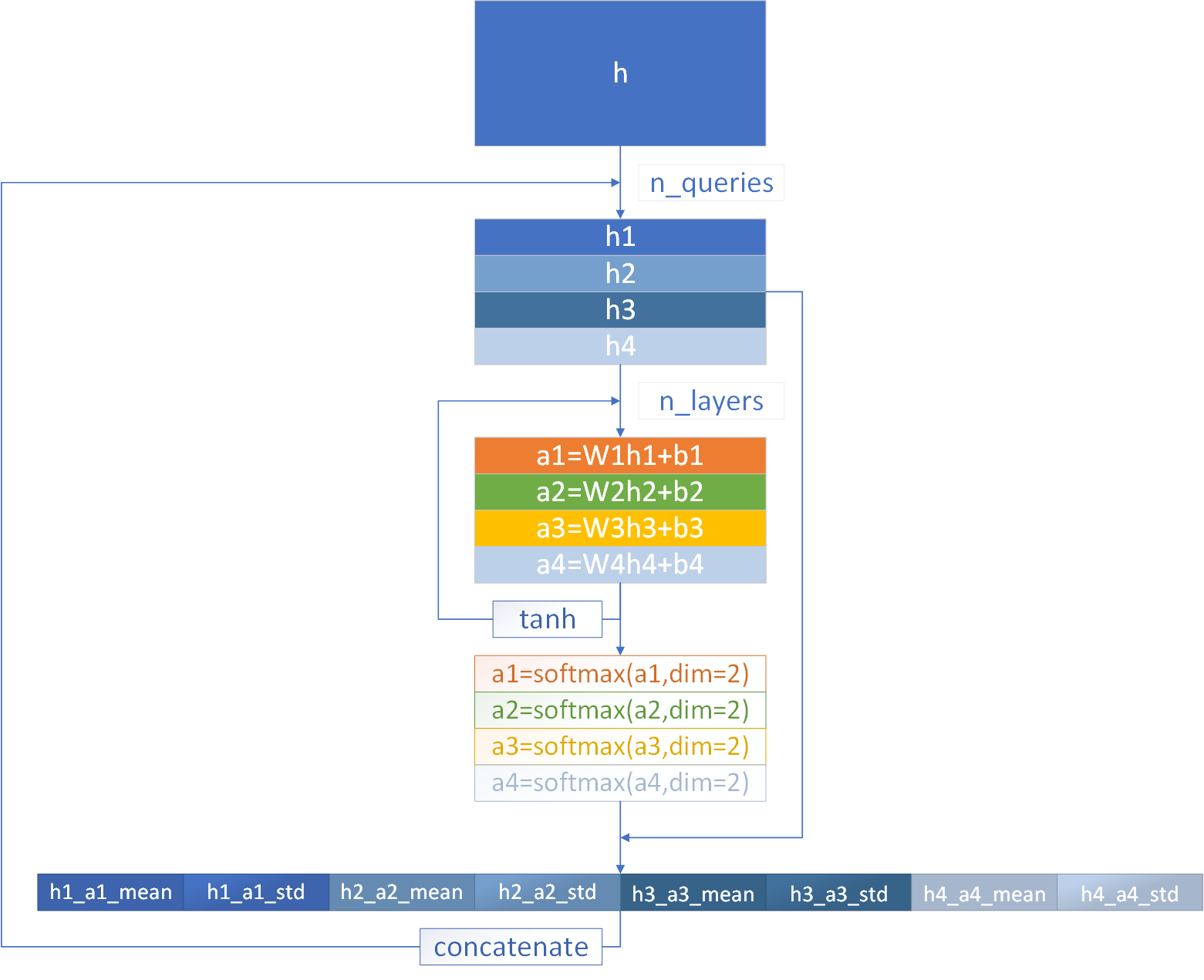
• MQMHASTP（Multi-query multi-head attention pooling）是2022年提出的，带有多查询多头注意力的时序池化
  

• 输入特征图仍然记为h，假设维度为$(bs,5120,T)$，不再考虑bs维度

• 将h在特征维度上均等划分为$h$份，每一份是一个head，上图的$h=4$，也就是得到了h1，h2，h3，h4四个特征图，每个特征图的维度为$(bs,d_h,T)$，$d_h=5120//h$，实际使用时，输入特征图的特征维度应确保能被$h$整除

• 对h1，h2，h3，h4每个特征图都进行1维卷积，即上图的$W\times h+b$，得到对应的Attention分数a1，a2，a3，a4，这一部分的运算可以重复$n\text{-}layers$次

  • 当$n\text{-}layers=1$，1维卷积只进行一次，参数为$(in=d_h,out=1,ksize=1)$，因此每个Attention分数的维度为$(bs,1,T)$，卷积后不接激活函数
  • 当$n\text{-}layers=2$，1维卷积进行两次，激活函数进行一次
    • 第一次卷积参数为$(in=d_h,out=F,ksize=1)$，因此每个Attention分数的维度为$(bs,F,T)$，本次卷积会减少特征维度，因此$F<d_h$，F可取64
    • 接tanh激活函数
    • 第二次卷积参数为$(in=F,out=d_h,ksize=1)$，因此每个Attention分数的维度为$(bs,d_h,T)$，本次卷积会恢复特征维度

• 对每个Attention分数，都在frame维度，接softmax激活函数，此时Attention分数的每一行，求和都等于1，而且每个Attention分数与对应的head，维度都相同。可以将Attention分数作为权重，计算每个head的Attention均值和标准差，计算公式如下，与上述的ASTP公式类似
  $$\begin{array}{rl}{\mu }^h& =\sum _{t=1}^T{\alpha }_t^h{h}_t^h\\ {\sigma }^h& =\sqrt{\sum _{t=1}^T{\alpha }_t^h{h}_t^h\odot h_t^h-{\mu }^h\odot {\mu }^h}\end{array}$$

• 每个head的Attention均值和标准差的维度都为$(bs,d_h)$，按照head的顺序，交替地将mean和std串联起来，输出维度为$(bs,h\ast d_h\ast 2)=(bs,5120\ast 2)$

• 对于上述的划分head、计算每个head的Attention分数、计算每个head的Attention统计量、串联每个head的Attention统计量，四个步骤，会进行$n\text{-}queries$次，每次的输出维度都是$(bs,5120\ast 2)$，因此MQMHASTP的最终输出维度为$(bs,n\text{-}queries\ast h\ast d_h\ast 2)=(bs,n\text{-}queries\ast 5120\ast 2)$