目录
- 理论解读
- CRC应用
- CRC算法参数解读
- 常见CRC参数模型
- 设计实战
- 校招编程题
- 分类
- 串行输入、并行计算、串行输出**
- 串行计算、串行输出(线性移位寄存器)
- LSFR线性移位寄存器(并转串)(并行计算)
- 模二除
- 总结——串行、并行计算的本质
- 参考链接
理论解读
CRC应用
CRC即循环冗余校验码(Cyclic Redundancy Check):是数据通信领域中最常用的一种查错校验码,其特征是信息字段和校验字段的长度可以任意选定。循环冗余检查(CRC)是一种数据传输检错功能,对数据进行多项式计算,并将得到的结果附在帧的后面,接收设备也执行类似的算法,以保证数据传输的正确性和完整性。
CRC算法参数解读
- NAME:参数模型名称。
- WIDTH:宽度,即CRC比特数。
- POLY:生成项的简写,以16进制表示。例如:CRC-32即是0x04C11DB7,忽略了最高位的"1",即完整的生成项是0x104C11DB7。
- INIT:这是算法开始时寄存器(crc)的初始化预置值,十六进制表示。
- REFIN:待测数据的每个字节是否按位反转,True或False。
- REFOUT:在计算后之后,异或输出之前,整个数据是否按位反转,True或False。
- XOROUT:计算结果与此参数异或后得到最终的CRC值。
常见CRC参数模型

设计实战
校招编程题
(2021乐鑫科技数字IC提前批代码编程)
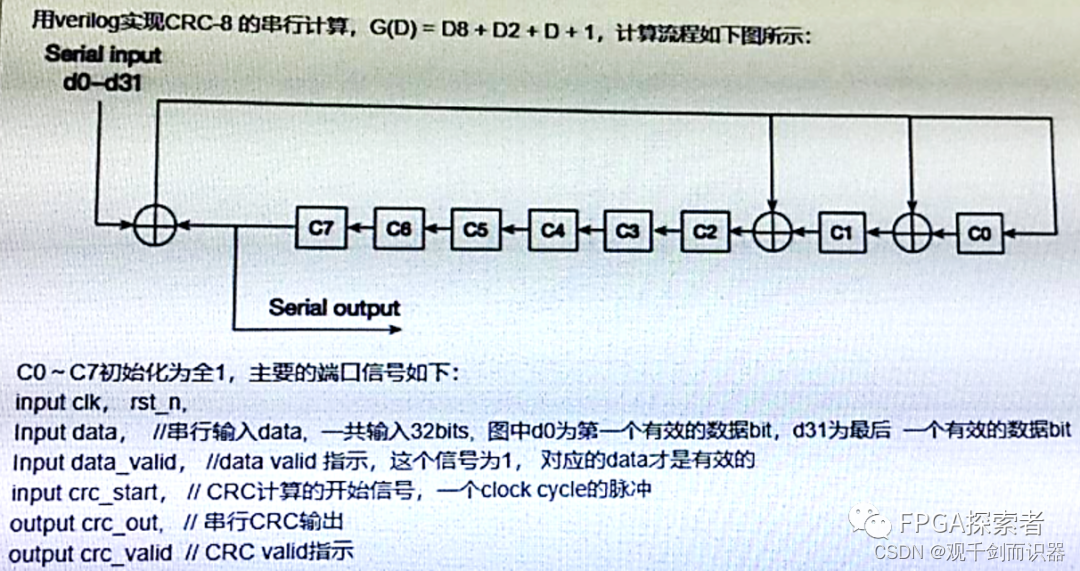
- 用Verilog实现CRC-8的串行计算,G(D)=D8+D2+D+1,计算流程如下图所示:
分类
串行输入、并行计算、串行输出**
-
手算

-
计算器

-
代码
module crc_8(
input clk,
input rst,
input data_in,
input data_valid,
input crc_start,
output reg crc_out,
output reg crc_valid
);
reg [7:0] lfsr_q;
reg [7:0] lfsr_c;
always @(*)begin
lfsr_c[0] = lfsr_q[7] ^ data_in;
lfsr_c[1] = lfsr_q[0] ^ lfsr_q[7] ^ data_in;
lfsr_c[2] = lfsr_q[1] ^ lfsr_q[7] ^ data_in;
lfsr_c[3] = lfsr_q[2];
lfsr_c[4] = lfsr_q[3];
lfsr_c[5] = lfsr_q[4];
lfsr_c[6] = lfsr_q[5];
lfsr_c[7] = lfsr_q[6];
end
always @ (posedge clk)begin
if(rst) begin
lfsr_q <= {8{1'b0}};
end else begin
lfsr_q <= data_valid ? lfsr_c : lfsr_q;
end
end
reg [2:0] count;
always @ (posedge clk) begin
if(rst) begin
crc_out <= 0;
count <= 0;
end else begin
if(data_valid) begin
crc_out <= data_in;
crc_valid <= 1'b0;
end else if(crc_start)begin
count <= count + 1'b1;
crc_out <= lfsr_q[7-count];
crc_valid <= 1'b1;
end else begin
crc_valid <= 1'b0;
end
end
end
endmodule
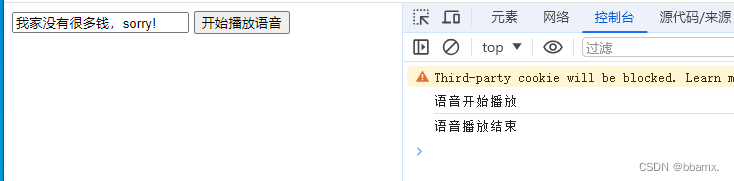
- 仿真结果

串行计算、串行输出(线性移位寄存器)
- 代码
module CRC_8(
input clk,
input rst,
input data_in,
input data_valid,
input crc_start,
output reg crc_out,
output reg crc_valid
);
reg [7:0] crc_reg;
always @ (posedge clk)begin
if(rst) begin
crc_reg <= 8'h00;
end else begin
if(data_valid) begin
crc_reg <= next_crc(data_in, crc_reg);
end
end
end
reg [2:0] count;
always @ (posedge clk)begin
if(rst) begin
crc_out <= 0;
count <= 0;
end else begin
if(data_valid) begin
crc_out <= data_in;
crc_valid <= 1'b0;
end else if(crc_start)begin
count <= count + 1'b1;
crc_out <= crc_reg[7-count];
crc_valid <= 1'b1;
end else begin
crc_valid <= 1'b0;
end
end
end
function [7:0] next_crc;
input data_in;
input [7:0] current_crc;
begin
next_crc = {current_crc[6:0],1'b0} ^ ({8{current_crc[7]^data_in}} & (8'h07));
end
endfunction
endmodule
- 结果
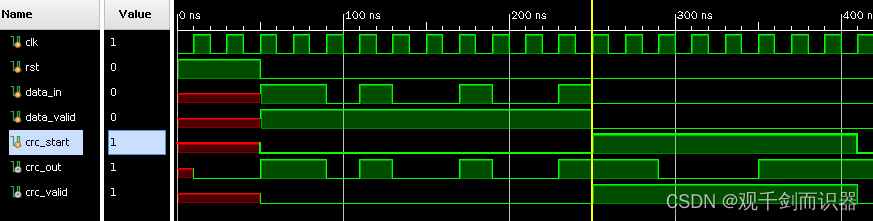
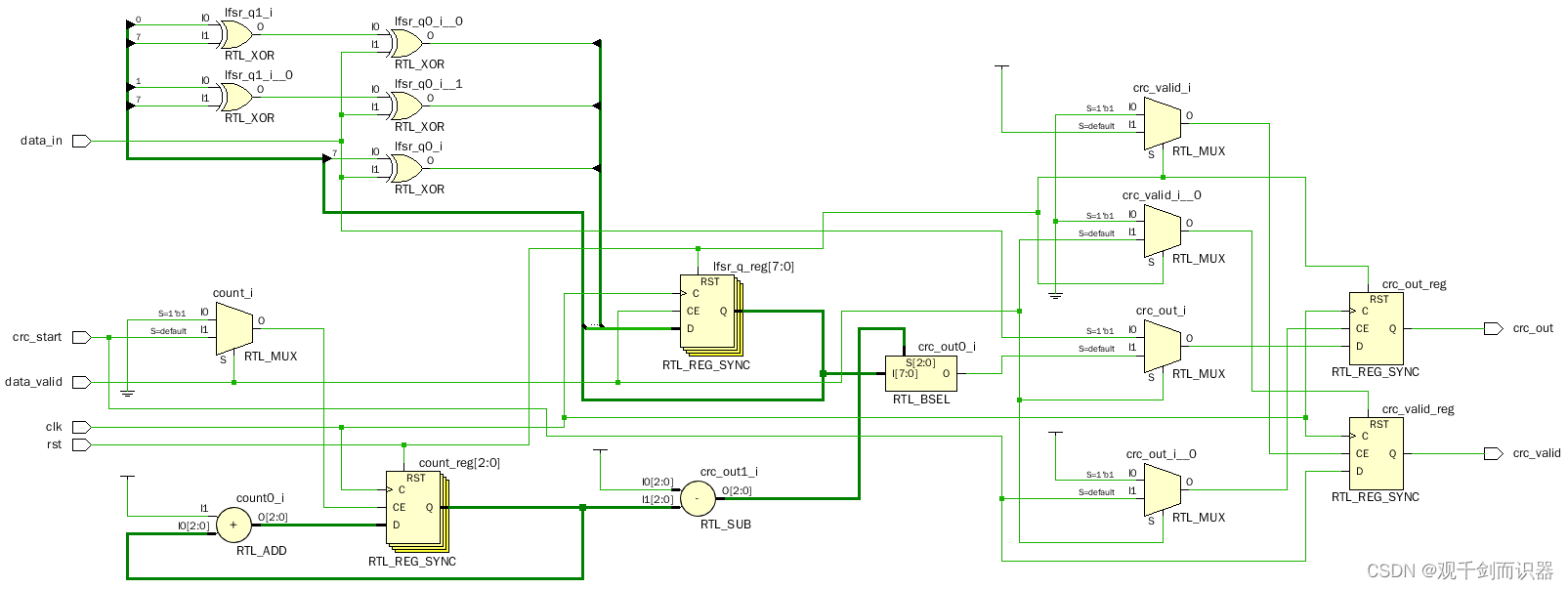
- 原理图
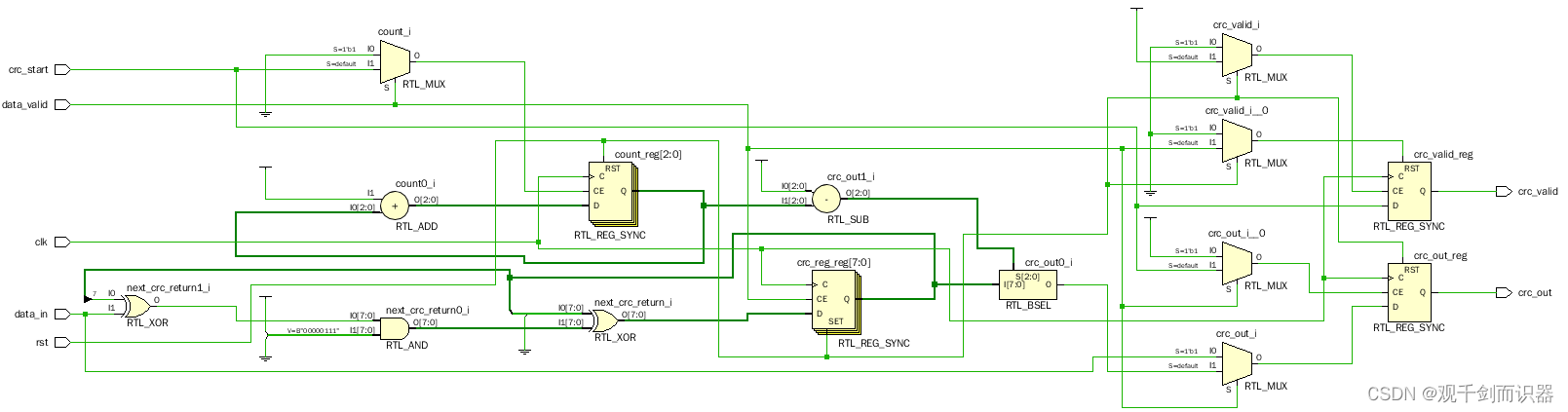
LSFR线性移位寄存器(并转串)(并行计算)
- 背景知识
首先得了解LFSR,线性反馈移位寄存器简称LFSR,用于产生可重复的伪随机序列,也可用来实现CRC校验。LFSR主要由触发器(寄存器)、异或门以及反馈线路组成。
通常推荐伽罗瓦LFSR,如图所示,对于二进制来说,gn 到g0的各个系数表示这条支路是否存在,1为存在,0则不存在。各个寄存器储存着上一次CRC校验运算的结果,寄存器的输出即为CRC的值。
已知多项弎gn x^n+ …+ g2 x^2+ g1 x^2 + g0,其中gn~g0 是系数,g0取直为1,其他系数可以是0或1。该多项式用二进制表示为i9n,9n-1……,9o),用LFSR表示为
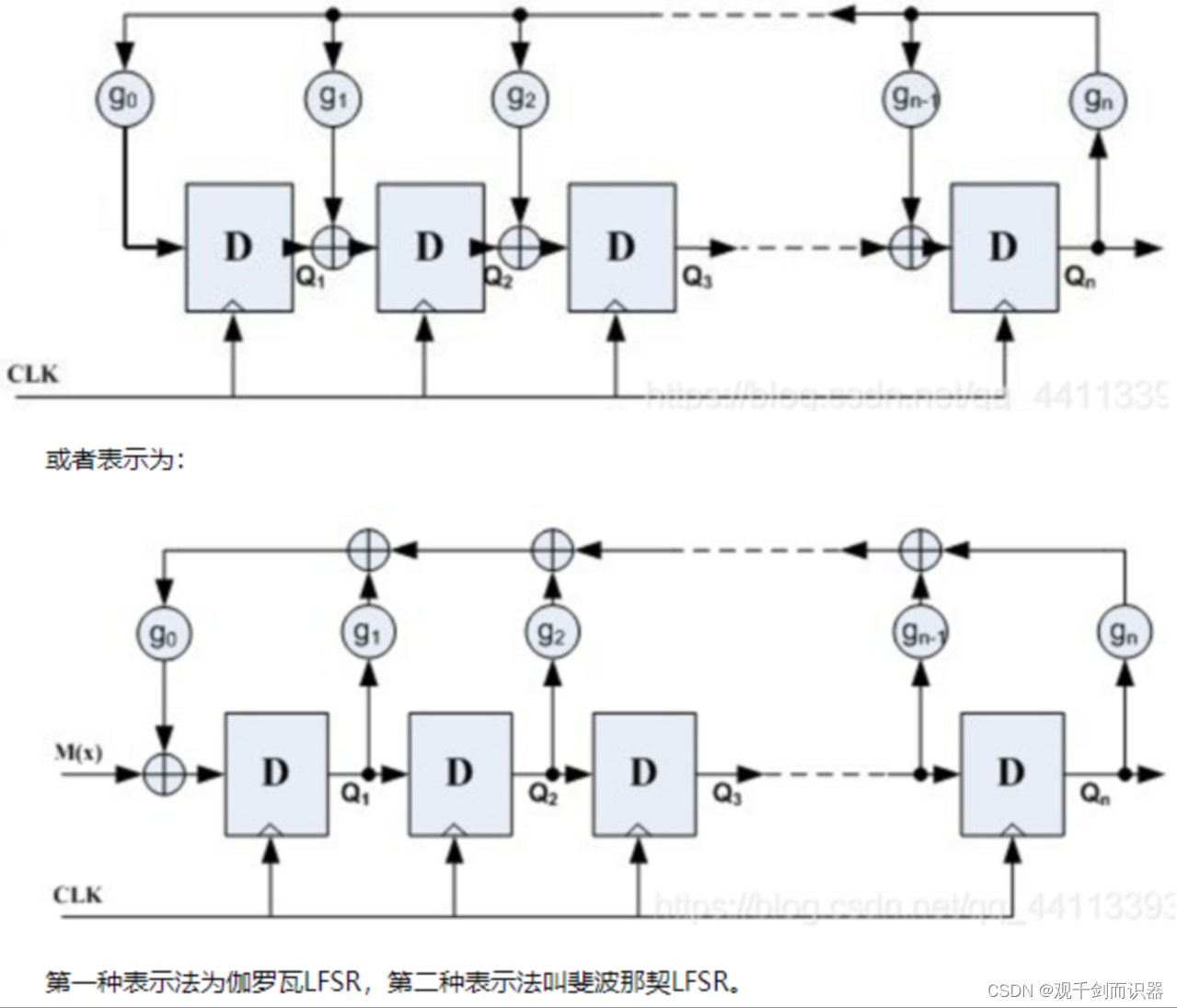
- 代码
//CRC=x16+x12+x5+x0
module CRC_GenSerial(
input clk,
input rst_n,
output reg [15:0] crc
);
reg [31:θ] data_parallel;
reg data_serial;
reg [5:0] cnt;
parameter source_data=32'h96E32077;
//并转串
always@(posedge clk or negedge rst_n) begin
if(!rst_n)begin
cnt <= 0;
data_parallel <= source_data;
data_serial <= 0;
end else if(cnt<32) begin
cnt<=cnt+1;
data_serial <= data_parallel[31];
data_parallel <= data_parallel<<1;
end else begin
cnt<=33;
data_serial <= 0;
data_parallel <= 0;
end
end
always @(posedge clk or negedge rst_n)begin
if(!rst_n)begin
crc<=0;
end else if(cnt<=32)begin
crc[D] <= crc[15]^data_serial;
crc[4:1] <= crc[3:0];
crc[5] <= crc[4]^crc[15]^data_serial;
crc[11:6] <= crc[10:5];
crc[12] <= crc[11]^crc[15]^data_serial;
crc[15:13] <= crc[14:12];
end else begin
crc<=crc;
end
end
endmodule
- 原理图
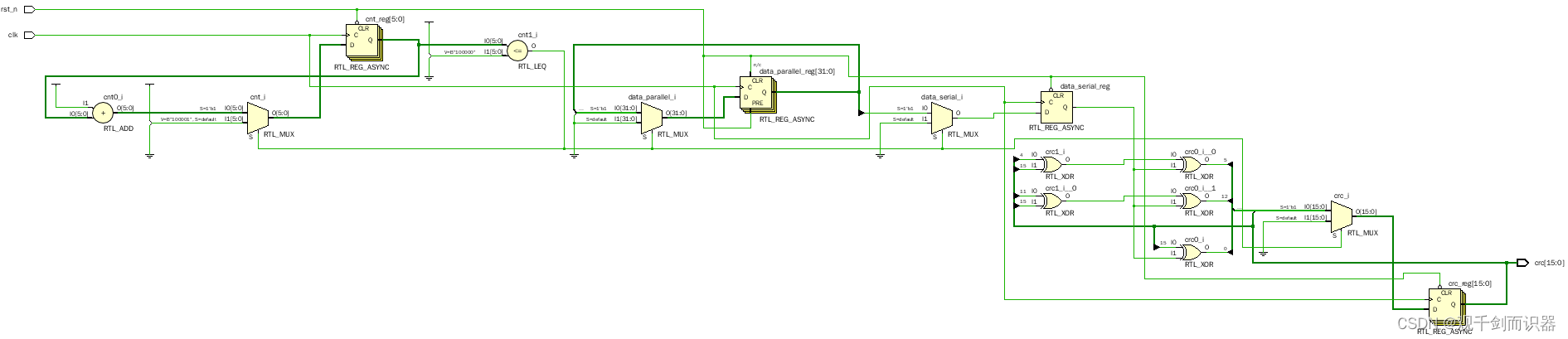
- 代码仿真

模二除
-
背景知识
CRC校验中的运算不是普通的运算,称为“模2运算” -
模2加法和减法都是异或运算,例子如下:
1010+0110=1100,1010-0110=1100 -
模2乘法的定义:
0×0=0,0×1=0,1×0=0,1×1=1。 1011×101=100111其中横线之间的累加过程,采用的是2进制加法,不进位。

-
模2除法,其实也是异或运算: 0/1=0,1/1=1。 1011/101=10,余数为100(补了2个0)。

-
代码
module CRC_Gen(
input clk,
input rst_n,
input [7:0] data,
input data_valid,
output reg [15:0] crc
);
reg [23:0] temp=0;
parameter polynomial=17b1_8001_0060_0810_0081;
always @(posedge clk or negedge rst_n)begin
if(!rst_n)begin
crc <= 0;
temp <= {data,16'b0};//复位时,将初始数据放入寄存器
end else if(data valid)begin
if(temp[23]) temp[23:7] <= temp[23:7] ^ polynomial;
else if(temp[22]) temp[22:6] <= temp[22:6] ^ polynomial;
else if(temp[21]) temp[21:5i <= temp[21:5i ^ polynomial;
else if(temp[20]) temp[20:4j <= temp[20:4] ^ polynomial;
else if(temp[19]) temp[19:3] <= temp[19:3i ^ polynomial;
else if(temp[18]) temp[18:2] <= temp[18:2] ^ polynomial;
else if(temp[17]) temp[17:1j <= temp[17:1] ^ polynomial;
else if(temp[16]) temp[16:oj <= temp[16:0] ^ polynomial;
else begin
crc<=temp[15:0];
end
end
endmodule
总结——串行、并行计算的本质
在第一段代码中,LFSR(线性反馈移位寄存器)的计算是在 always @(*) 块内部进行的。这里使用了组合逻辑的方式,并不受时钟信号的影响,因此是在数据信号变化时立即触发的,是并行计算的。每次数据信号 data_in 变化时,都会立即计算出 lfsr_c 寄存器的值,不需要等待时钟信号的上升沿。因此,LFSR 寄存器的更新是在数据信号变化时立即完成的,是并行计算的。
在第二段代码中,next_crc 函数是在 always @(posedge clk) 块内部被调用的,因此它的计算是在时钟的上升沿触发时进行的,这导致了计算是串行执行的。每个时钟周期,next_crc 函数都会被调用一次,并且在时钟的边沿执行。因此,整个 CRC 寄存器的更新是在时钟周期内完成的,是串行计算的。
从异或门调用的个数来看,串行计算要少得多
参考链接
- CRC(循环冗余校验)在线计算
- FPGA手撕代码——CRC校验码的多种Verilog实现方式
- CRC校验原理和推导过程及Verilog实现(一文讲透)
![[高质量]2024五一数学建模A题保奖思路+代码(后续会更新)](https://img-blog.csdnimg.cn/direct/6892c1bec9f64b97916a9872e4a43743.png)
![[C语言]典型例题:小蚂蚁爬橡皮筋、买汽水问题、导致单词块、菱形打印……](https://img-blog.csdnimg.cn/direct/559c20ed0664420cbe8d06083f39d0a0.png)