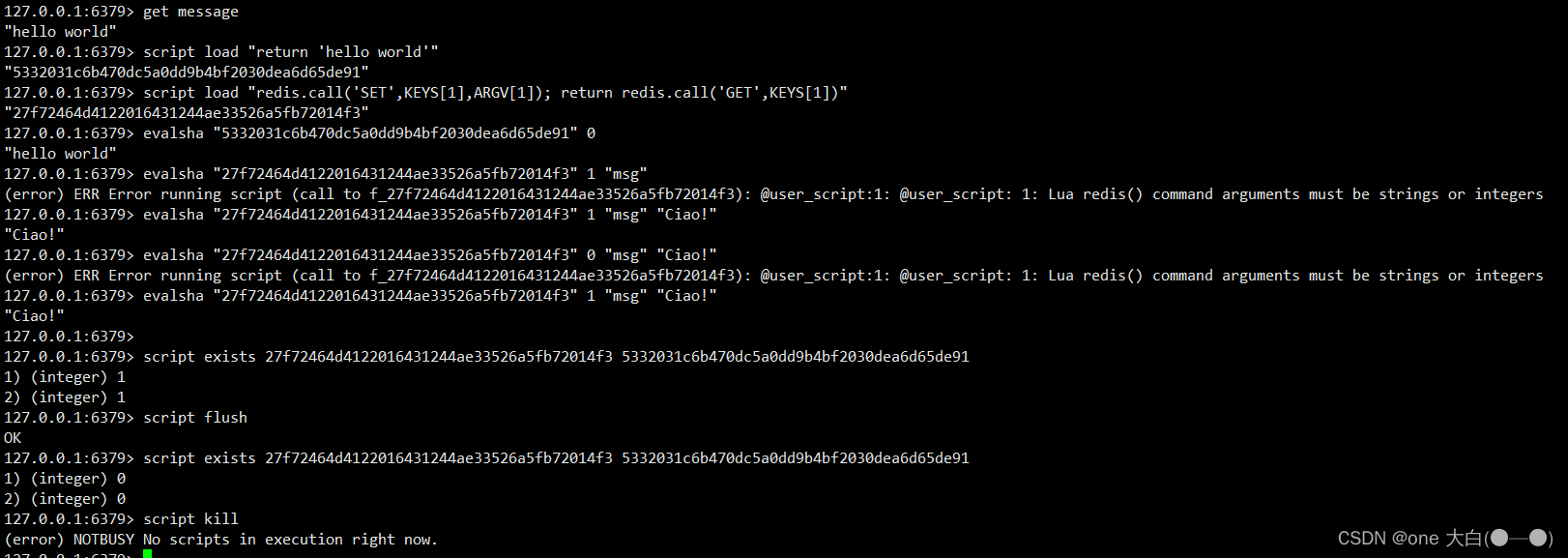
题干
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]] 输出:1
解题思路
这道题目我一开始被误导了,以为不用自己创建棋盘,只用题目给出的棋盘就可以了,但是很明显这不可行,因为障碍物的坐标的值应该为0而不是1,0意味着没有路径可以到达障碍物。
事实上,我们可以把题目给的棋盘当作地图,上面标记了障碍物的位置,这样也不需要在自己的棋盘上标记障碍物了,只要对照着地图看就行了,是不是很妙。
1.首先确定dp数组的含义
dp[i][j]为到[i][j]点的路径总和
2.确定递推公式
if(obstacleGrid[i][j] == 1)
continue;
dp[i][j] = dp[i-1][j] + dp[i][j-1];
如果遇到障碍物直接跳过,保留值为0
3.dp数组的初始化
这一次我们用卡尔的办法来初始化。
第一行障碍物前的全为1,第一列障碍物前的全为1

4.确定递推顺序
从递推公式可以看出,状态由左边和上边的状态推到而来,用从左至右,从上至下的两层循环即可
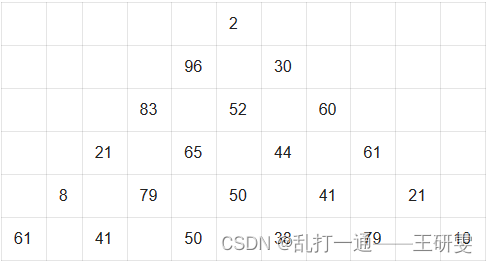
5.举例推导dp数组
3*6的棋盘的数组的结果应该如下

完整代码如下
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
//获取行的个数
int m = obstacleGrid.size();
//获取列的个数
int n = obstacleGrid[0].size();
//剪枝:如果起点和终点都有障碍物,return 0
if(obstacleGrid[0][0] == 1|| obstacleGrid[m-1][n-1] == 1)
return 0;
//建立全为0的棋盘
vector<vector<int>> dp(m, vector<int>(n, 0));
//想要找到障碍物的位置比较麻烦,不如全部初始化为0,遇到障碍物保持0
//初始化 拿着地图看,第一行障碍物前的全为1
for(int i = 0; i < m && obstacleGrid[i][0] == 0; i++){
dp[i][0] = 1;
}
//初始化 拿着地图看,第一列障碍物前的全为1
for(int j = 0; j < n && obstacleGrid[0][j] == 0; j++){
dp[0][j] = 1;
}
//遍历
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
//拿地图对照,如果是障碍物
if(obstacleGrid[i][j] == 1)
continue;
//递推公式
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};ps:用变量来建立静态数组是不行的,所以要创建动态的二维数组
vector<vector<int>> dp(m, vector<int>(n, 0));
格式:vector<vector<int> >swp(n,vector<int>(m));//定义二维数组swp[][],n行 m列










![[ log日志画图]分割模型训练结束生成相关日志运用代码画图](https://img-blog.csdnimg.cn/direct/590f108d1e8c40e3bbb139578d054049.png)