数据结构——栈的应用
- 括号匹配
- 中缀转后缀
- 什么是中缀后缀
- 中缀表达式 (Infix Notation)
- 后缀表达式 (Postfix Notation, Reverse Polish Notation, RPN)
- 加减,乘除运算
- 处理括号
- 后缀转中缀
我们今天来看栈的应用:
括号匹配
栈一个经典的应用就是括号匹配:
https://leetcode.cn/problems/valid-parentheses/description/


我们遇到的字符串可能更复杂,比如像:([{{{()]]{}(}}}{}
首先我们知道的,一个左括号如果要匹配,必须要有对应的右括号,而且是匹配最近的,而且最里面的左括号优先匹配对应的右括号(从最里面开始匹配,方便我们的检测,如果从最外面开始,会比较费劲)

所以我们思想是这样的:
1.凡是遇到左括号就入栈
2. 一旦遇到右括号,就弹出进行对应匹配,如果匹配,则弹出,否则返回无效
3. 最后,扫描完并且栈为空,说明这是合法的括号字符串
class Solution {
public:
bool isValid(string s)
{
//判断字符串的长度
int lenghth = s.size();
if(lenghth % 2 != 0)
return false;
stack<char> st;
//左括号入栈
for(int i = 0; i < lenghth ; i++)
{
if(s[i] == '(' || s[i] == '{' || s[i] == '[')
{
st.push(s[i]);
}
else
{
if(st.empty()) return false;
if (s[i] == ')' && st.top() != '(') return false;
if (s[i] == '}' && st.top() != '{') return false;
if (s[i] == ']' && st.top() != '[') return false;
st.pop();
}
}
return st.empty();
}
};
如果学习过unordered_map还可以这样玩:
class Solution {
public:
bool isValid(string s)
{
int lenghth = s.size();
if(lenghth % 2 != 0)
return false;
unordered_map<char, char> pairs = {
{')', '('},
{']', '['},
{'}', '{'} //形成键值对关系
};
stack<char> st;
for(auto ch : s)
{
if(pairs.count(ch))
{
if(st.empty() || st.top() != pairs[ch])
{
return false;
}
st.pop();
}
else
{
st.push(ch);
}
}
return st.empty();
}
};
中缀转后缀
什么是中缀后缀
中缀表达式和后缀表达式是两种不同的数学表达式表示方法,它们在结构和计算方式上有所区别。下面分别对这两种表达式进行详细解释:
中缀表达式 (Infix Notation)
定义:
中缀表达式是我们日常生活中最常用的数学表达式书写形式,其中运算符位于其作用的两个操作数之间。这种表达方式之所以被称为“中缀”,是因为运算符处于操作数的中间位置。
示例:
3 + 4 * 5
(10 / 2) - 3
在这两个例子中,“+”、“*”、“/”和“-”分别是中缀运算符,它们位于相关操作数之间。
特点:
- 符合人类自然阅读和书写的习惯,直观易懂。
- 计算中缀表达式时需要遵循特定的运算顺序规则,如先乘除后加减、同级运算符从左到右等,以及括号来改变默认优先级。
- 由于依赖运算符优先级和结合性,计算机在处理中缀表达式时通常需要额外的解析步骤来确定正确的计算顺序。
后缀表达式 (Postfix Notation, Reverse Polish Notation, RPN)
定义:
后缀表达式(又称为逆波兰表示法)是一种运算符置于其作用的操作数之后的表达式形式。在这种表示法中,不再需要括号来明确运算顺序,因为每个运算符都是在其所需的所有操作数已经出现之后才出现的。
示例:
3 4 5 * +
10 2 / 3 -
这里,“*”、“+”、“/”和“-”同样是运算符,但它们现在出现在各自操作数之后。
特点:
- 后缀表达式消除了对括号的需求,因为其结构已经明确指定了运算顺序:从左到右扫描表达式,遇到数字时直接压入堆栈,遇到运算符时弹出堆栈中足够的操作数进行计算,并将结果压回堆栈。
- 计算机可以直接按照从左到右的顺序遍历来计算后缀表达式,无需复杂的优先级判断,因此非常适合机器处理,尤其是在需要高效计算的场合。
- 对于人类阅读者来说,后缀表达式不如中缀表达式直观,但其计算逻辑简洁且易于编程实现。
转换与计算:
将中缀表达式转换为后缀表达式通常涉及使用栈数据结构来处理运算符的优先级和结合性。转换完成后,后缀表达式可以直接通过一个简单的栈机制进行计算,无需复杂的解析过程。
总结来说,中缀表达式是人们习惯的数学书写方式,直观易读但计算时需考虑运算符优先级;而后缀表达式虽然对人不太直观,但其结构清晰、计算简单,特别适用于计算机自动化处理。
现在给你一个中缀表达式要求你转成后缀表达式:
https://www.nowcoder.com/practice/4e7267b55fdf430d9403aa12206572b3?tpId=182&tqId=34663&ru=/exam/oj
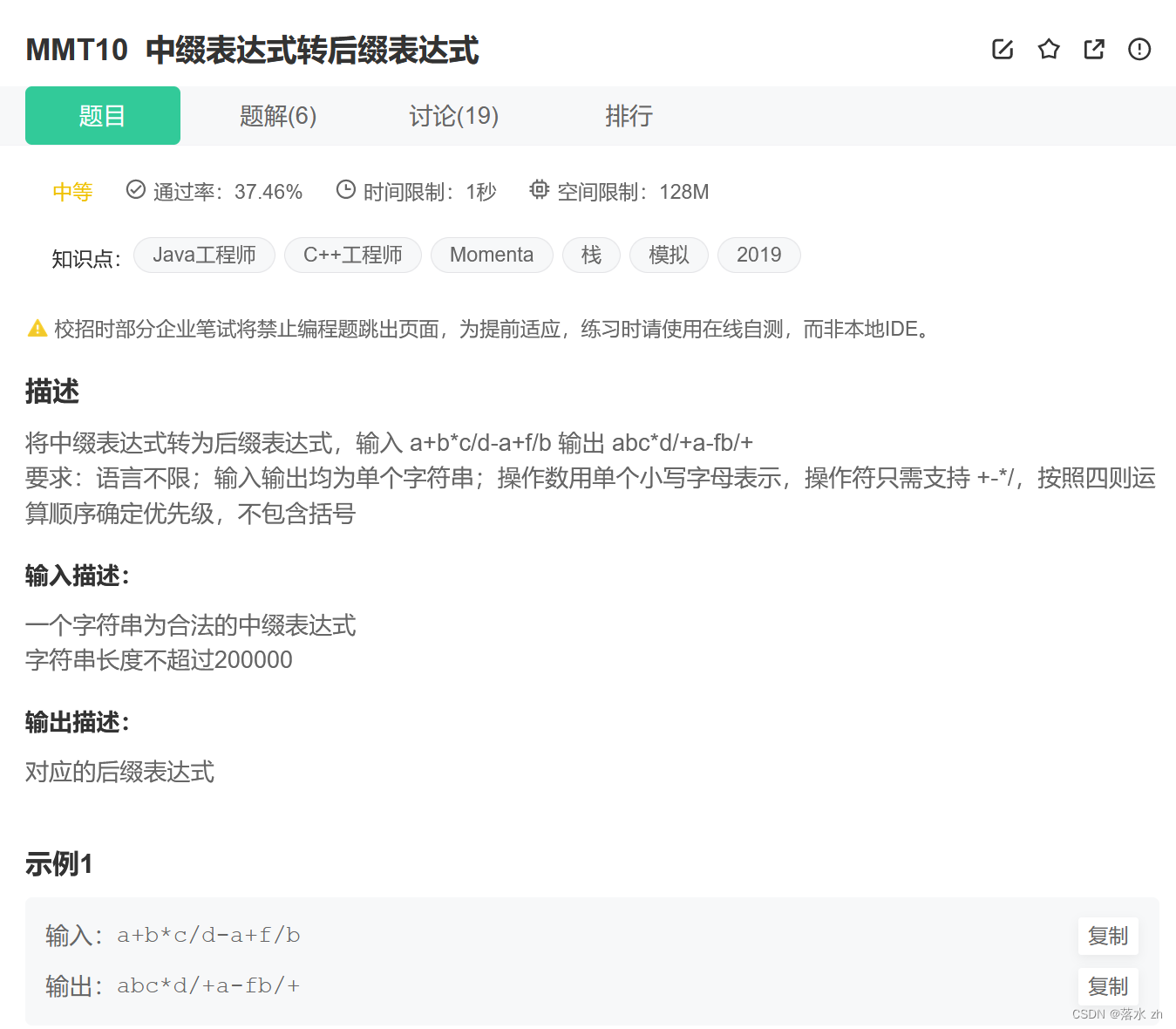
我们先从简单的开始:

加减,乘除运算
加减,乘除运算,乘除运算是比加减运算级高的,所以我们在入栈的时候,要考虑运算符的优先顺序:
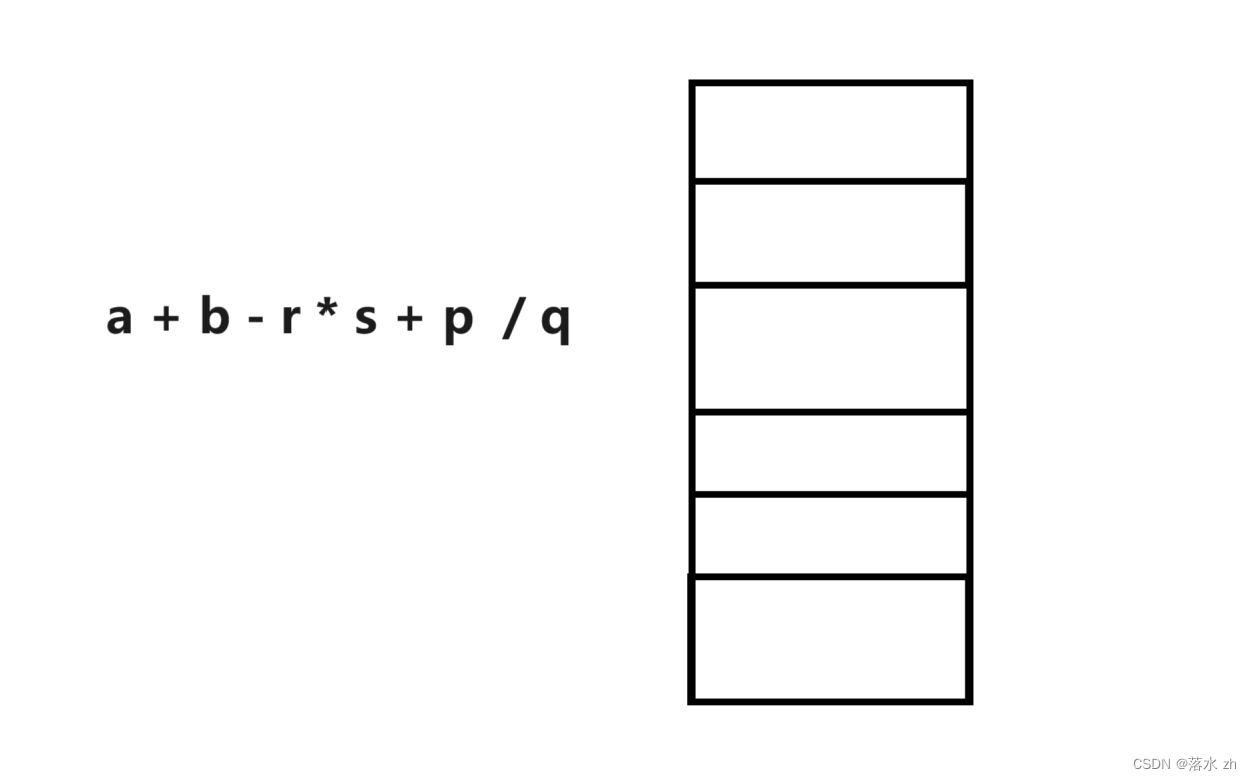
还是和之前一样,如果为操作数,直接打印:
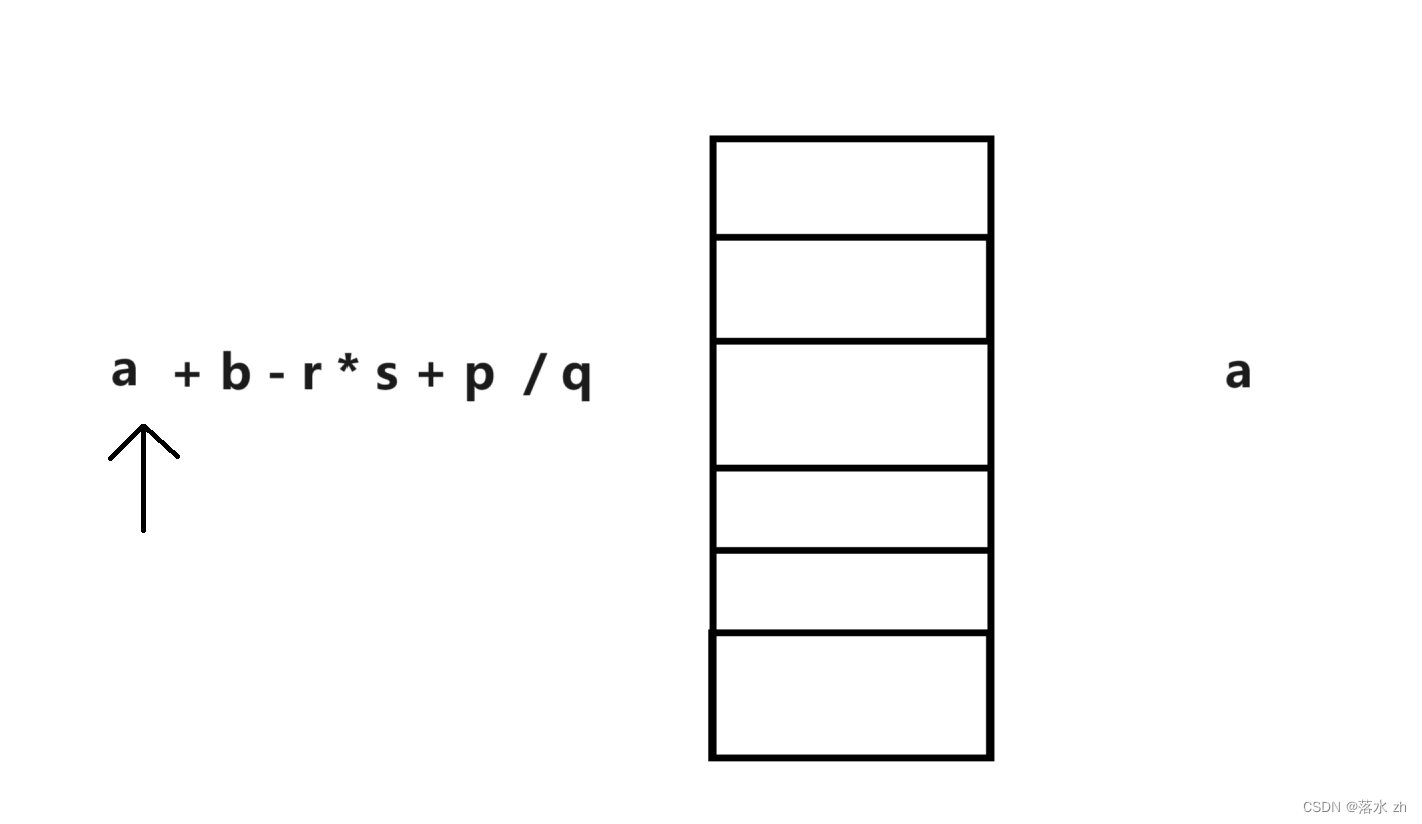
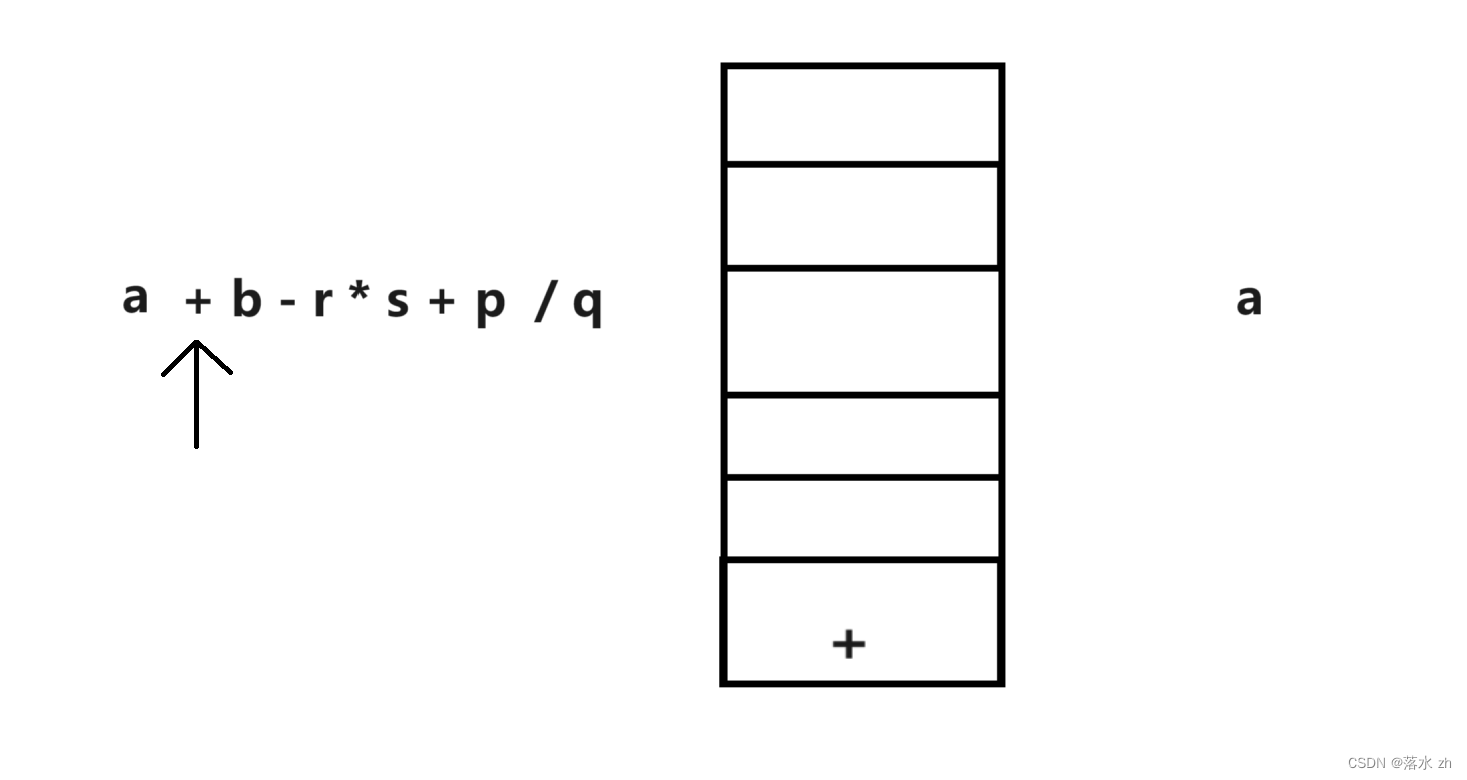
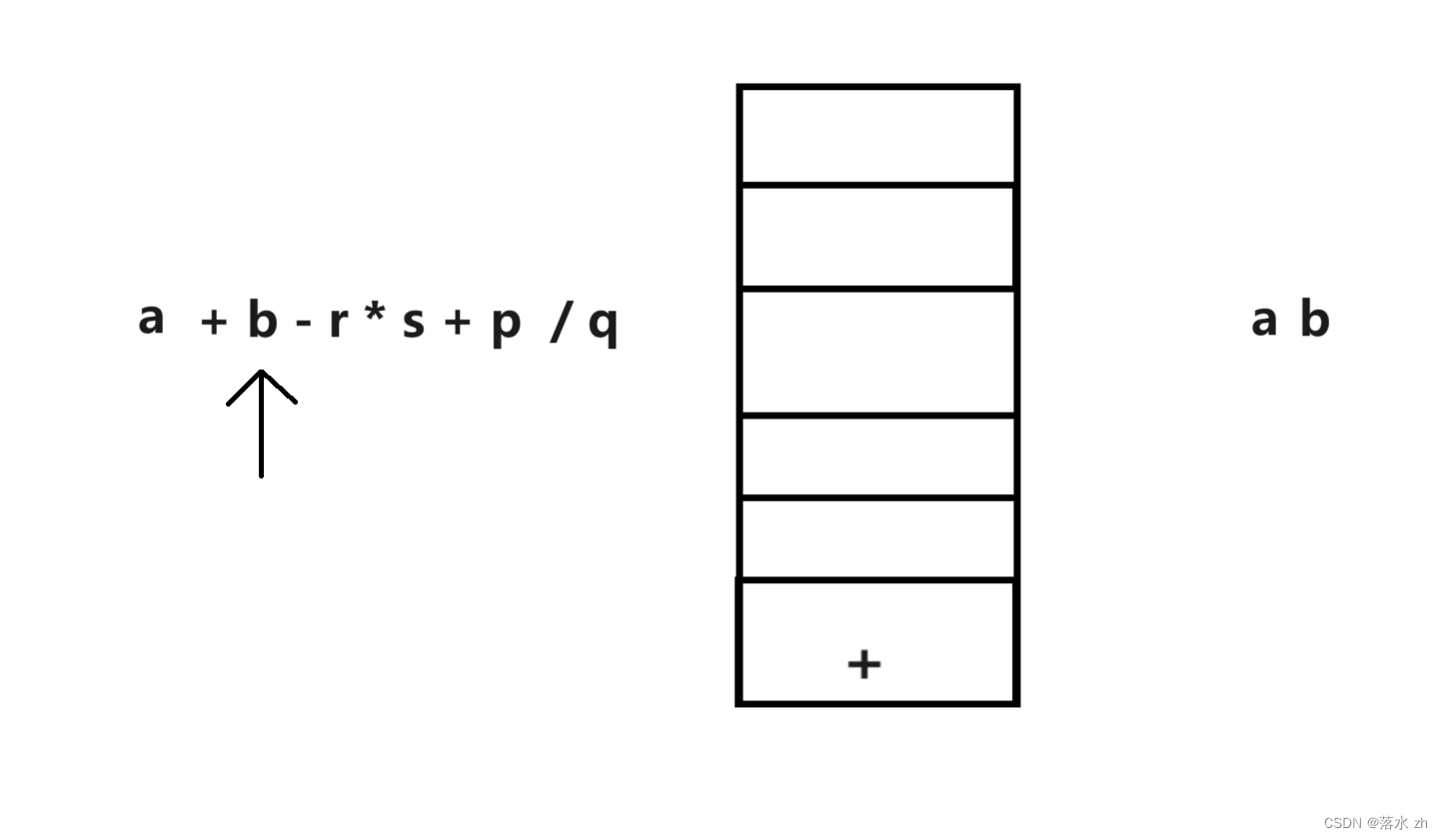
这个时候,- 号的优先级和+号一样,说明在此时+可以完成了动作,所以出栈:
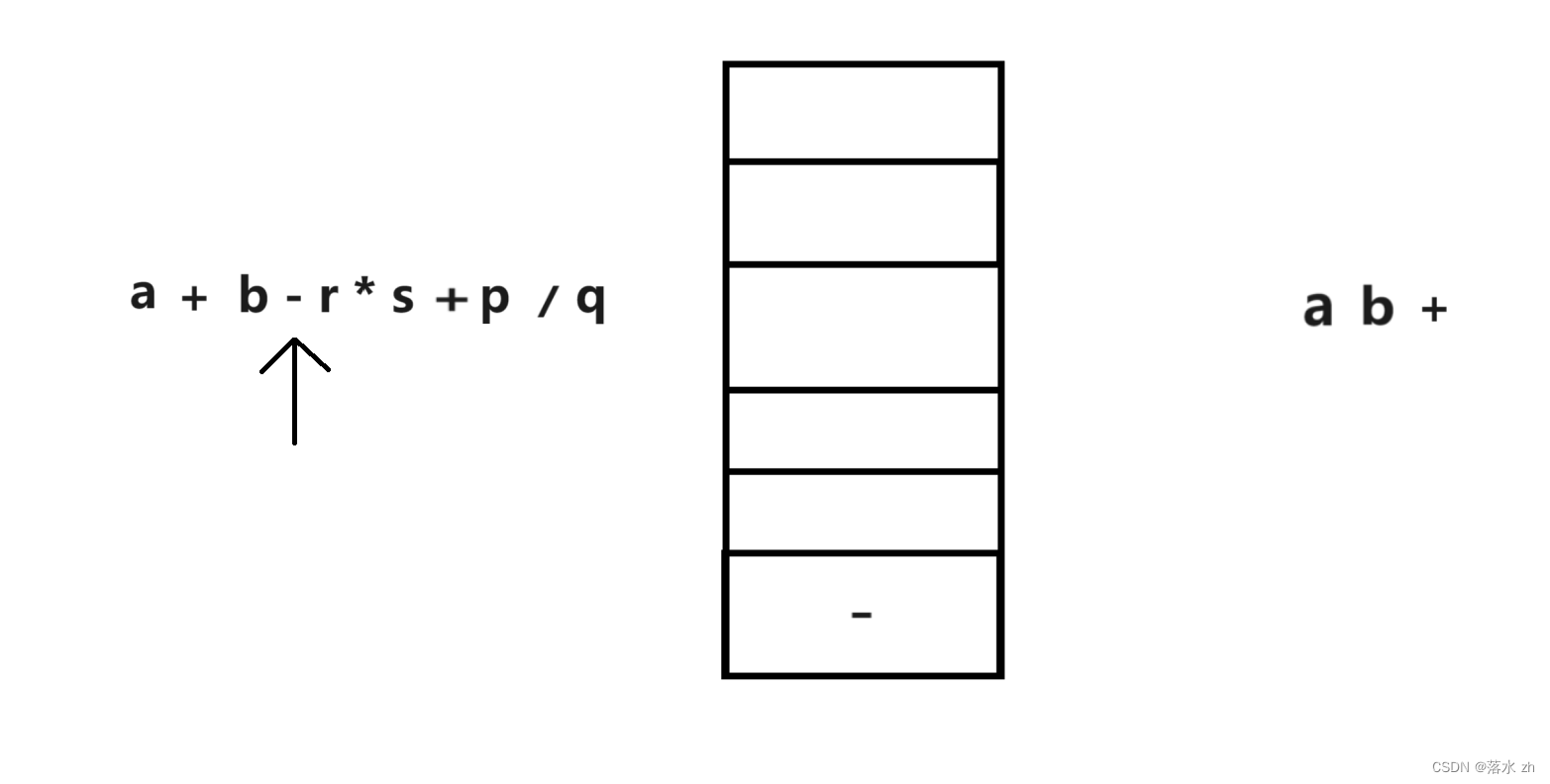
之后继续向后走:
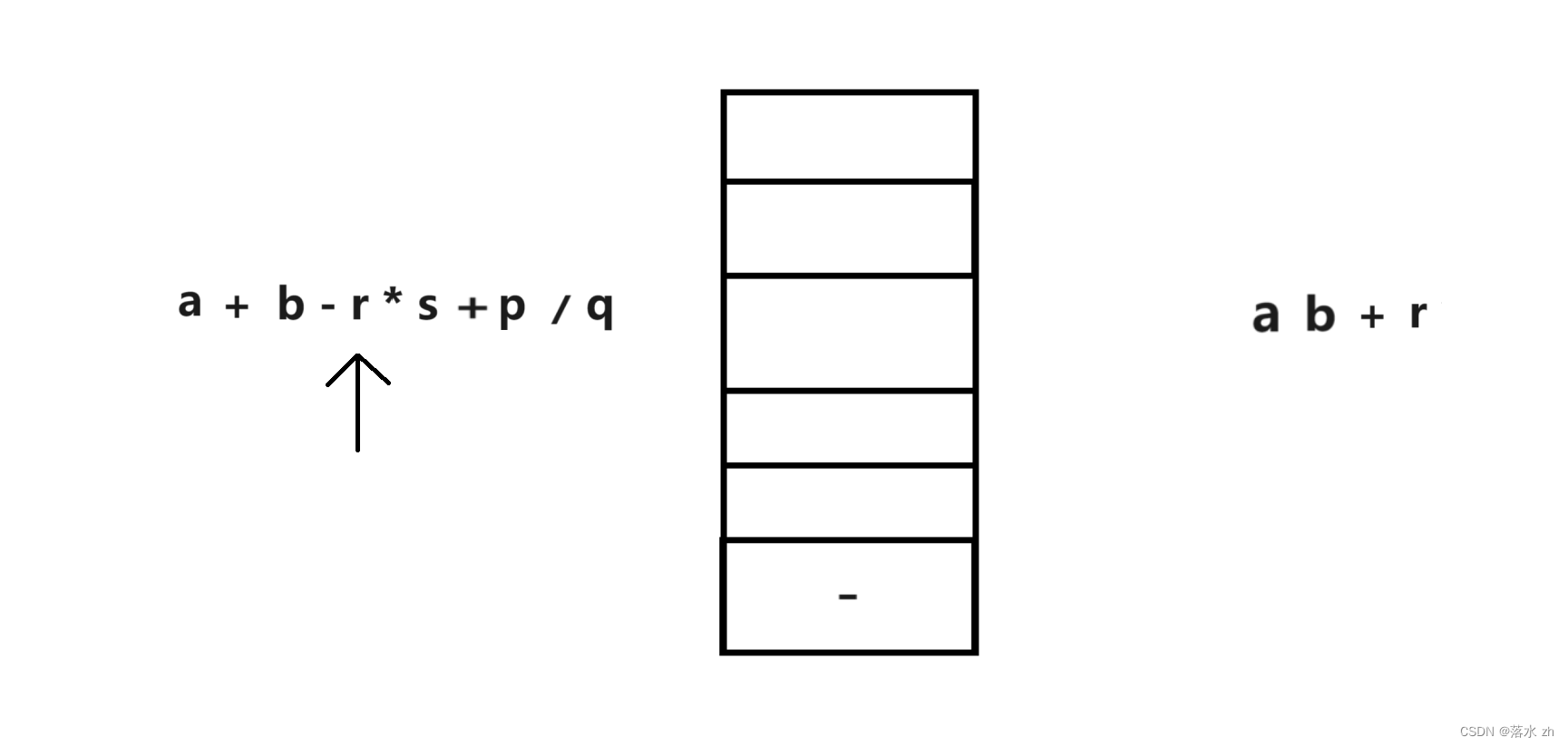
这个时候遇到了乘号,比栈顶元素的优先级高,先入栈
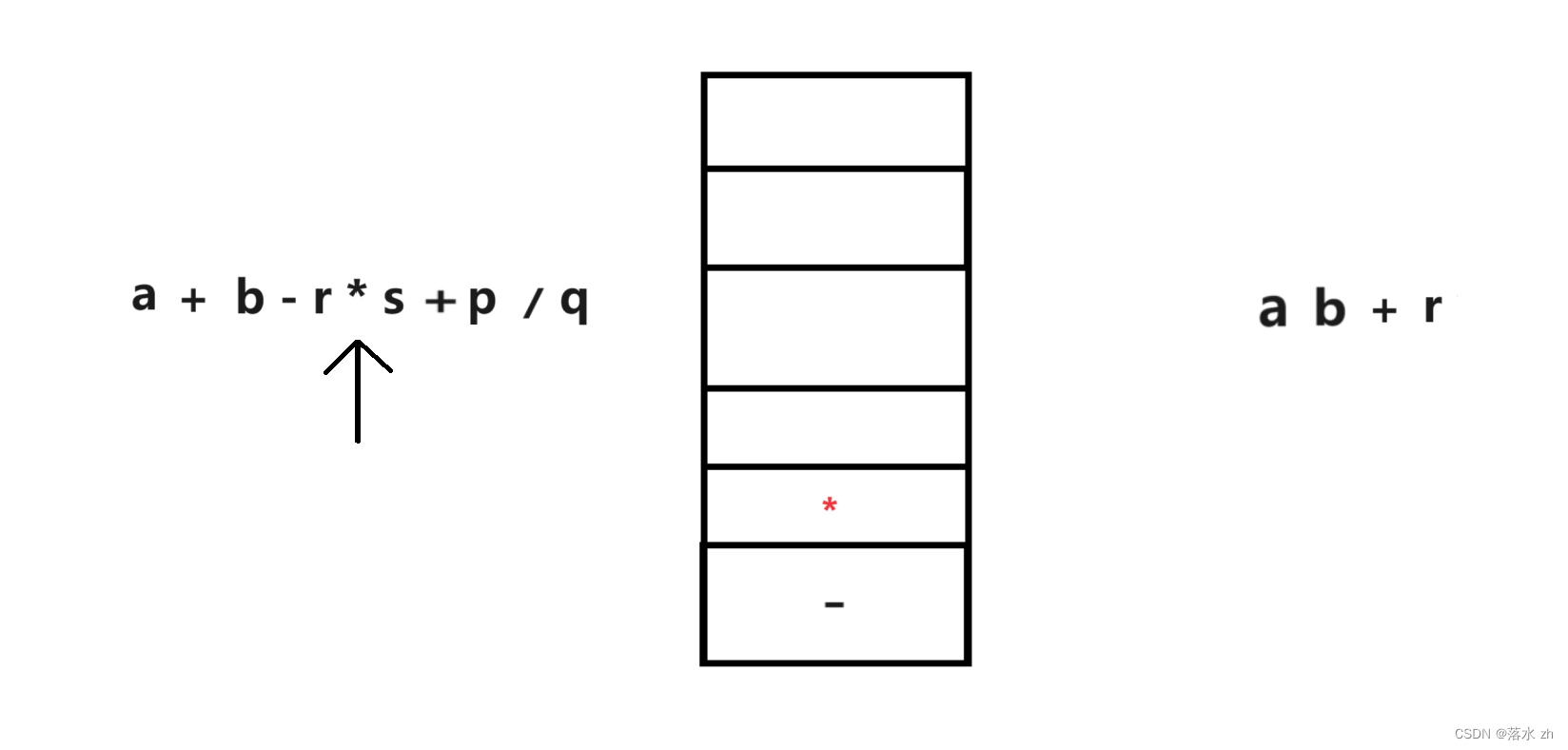
当前操作符的优先级高于栈顶运算符时,表明栈顶运算符应当在其之后完成计算。因此,为了保持正确的运算顺序,应该先将当前高优先级运算符压入栈中,待将来可能遇到的更低优先级运算符(或者遇到栈顶运算符的右括号对)时再将其弹出。这样确保了高优先级运算符始终晚于低优先级运算符出栈,符合后缀表达式的构建规则。
之后重复上面的步骤,我们就可以得到完整的后缀表达式。总结一下:
- 初始化一个空的栈stk,用于存储操作符和左括号。
- 从左到右扫描中缀表达式的每个字符。
- 遇到操作数,将其添加到输出字符串中。
- 遇到操作符(+、-、*、/),则将其与栈stk顶的操作符进行优先级比较:
a. 如果栈stk为空,则将操作符压入栈stk。
b. 如果操作符的优先级高于栈顶操作符,则将操作符压入栈stk。
c. 如果操作符的优先级小于等于栈顶操作符,则将栈顶操作符弹出并添加到输出字符串中,然后重复步骤4。
当扫描完中缀表达式后,将栈stk中剩余的操作符依次弹出并添加到输出字符串中。
#include<iostream>
#include<string>
#include<stack>
#include <cctype>
#include<unordered_map>
using namespace std;
// 定义一个无序映射(哈希表),用于存储运算符及其优先级
unordered_map<char, int> pairs = {
{'+', 1}, // 加法优先级为1
{'-', 1}, // 减法优先级为1
{'*', 2}, // 乘法优先级为2
{'/', 2} // 除法优先级为2
};
// 函数声明:将输入的中缀表达式字符串转换为后缀表达式字符串
string infixToPostfix(const string &infix)
{
// 定义一个字符栈stk用于存储运算符
stack<char> stk;
// 初始化后缀表达式字符串postfix
string postfix;
// 遍历输入的中缀表达式字符串中的每个字符
for (char ch : infix)
{
// 如果字符为字母或数字(即操作数),直接添加到后缀表达式字符串中
if (isalnum(ch))
{
postfix += ch;
}
// 否则,假设当前字符为运算符
else
{
// 当栈非空,且当前运算符优先级小于等于栈顶运算符优先级时
while (!stk.empty() && pairs[ch] <= pairs[stk.top()])
{
// 将栈顶运算符弹出并添加到后缀表达式字符串中
postfix += stk.top();
stk.pop();
}
// 将当前运算符压入栈中
stk.push(ch);
}
}
// 当栈非空时,依次弹出栈顶运算符并添加到后缀表达式字符串中
while (!stk.empty())
{
postfix += stk.top();
stk.pop();
}
// 返回生成的后缀表达式字符串
return postfix;
}
int main()
{
// 定义并初始化中缀表达式字符串infix
string infix;
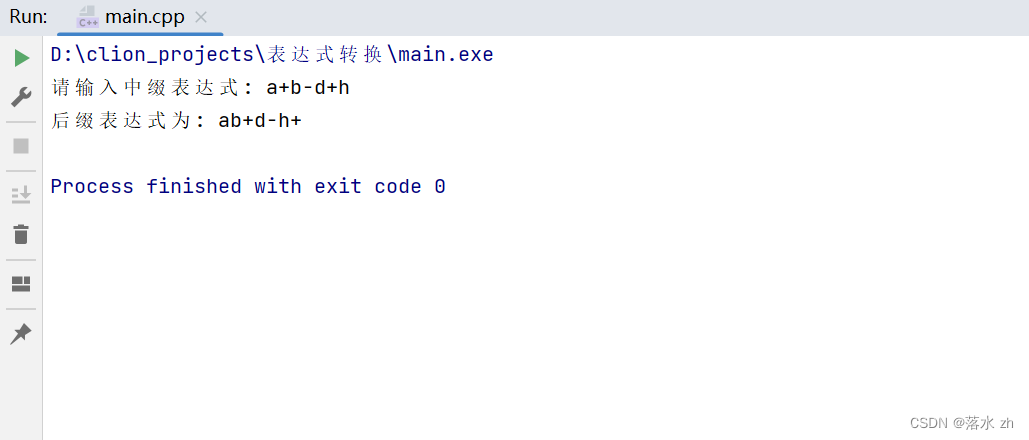
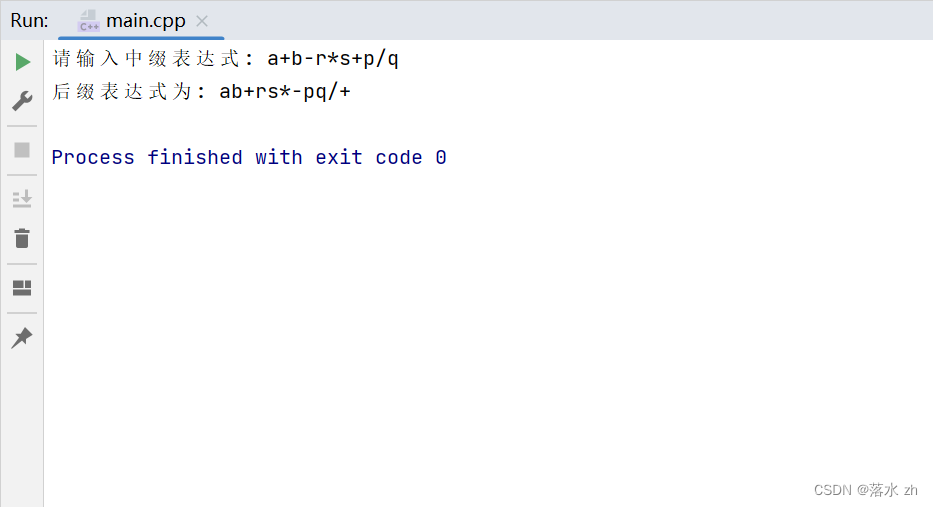
cout << "请输入中缀表达式: ";
cin >> infix;
// 调用infixToPostfix函数将输入的中缀表达式转换为后缀表达式,并存储在postfix变量中
string postfix = infixToPostfix(infix);
// 输出转换后的后缀表达式
cout << "后缀表达式为: "<< postfix<< endl;
// 程序结束,返回0
return 0;
}
处理括号
如果出现括号,我们可以理解为:括号可以提升优先等级,所以左括号直接入栈,直到遇到右括号,再依次弹出,直到把左括号也弹出栈:
#include<iostream>
#include<string>
#include<stack>
#include <cctype>
#include<unordered_map>
using namespace std;
// 定义一个无序映射(哈希表),用于存储运算符及其优先级
unordered_map<char, int> pairs = {
{'+', 1}, // 加法优先级为1
{'-', 1}, // 减法优先级为1
{'*', 2}, // 乘法优先级为2
{'/', 2} // 除法优先级为2
};
// 函数声明:将输入的中缀表达式字符串转换为后缀表达式字符串
string infixToPostfix(const string &infix)
{
// 定义一个字符栈stk用于存储运算符和括号
stack<char> stk;
// 初始化后缀表达式字符串postfix
string postfix;
// 遍历输入的中缀表达式字符串中的每个字符
for (char ch : infix)
{
// 如果字符为字母或数字(即操作数),直接添加到后缀表达式字符串中
if (isalnum(ch))
{
postfix += ch;
}
// 处理左括号:直接压入栈中
else if (ch == '(')
{
stk.push(ch);
}
// 处理右括号:
else if (ch == ')')
{
// 当栈非空,且栈顶元素不是左括号时,不断弹出栈顶元素并添加到后缀表达式字符串中
while (!stk.empty() && stk.top() != '(')
{
postfix += stk.top();
stk.pop();
}
// 弹出匹配的左括号(不添加到后缀表达式字符串)
stk.pop();
}
// 处理其他运算符(非括号):
else
{
// 当栈非空,且当前运算符优先级小于等于栈顶运算符优先级时
while (!stk.empty() && pairs[ch] <= pairs[stk.top()])
{
// 将栈顶运算符弹出并添加到后缀表达式字符串中
postfix += stk.top();
stk.pop();
}
// 将当前运算符压入栈中
stk.push(ch);
}
}
// 当栈非空时,依次弹出栈顶元素并添加到后缀表达式字符串中(此时栈中仅剩运算符)
while (!stk.empty())
{
postfix += stk.top();
stk.pop();
}
// 返回生成的后缀表达式字符串
return postfix;
}
int main()
{
// 定义并初始化中缀表达式字符串infix
string infix;
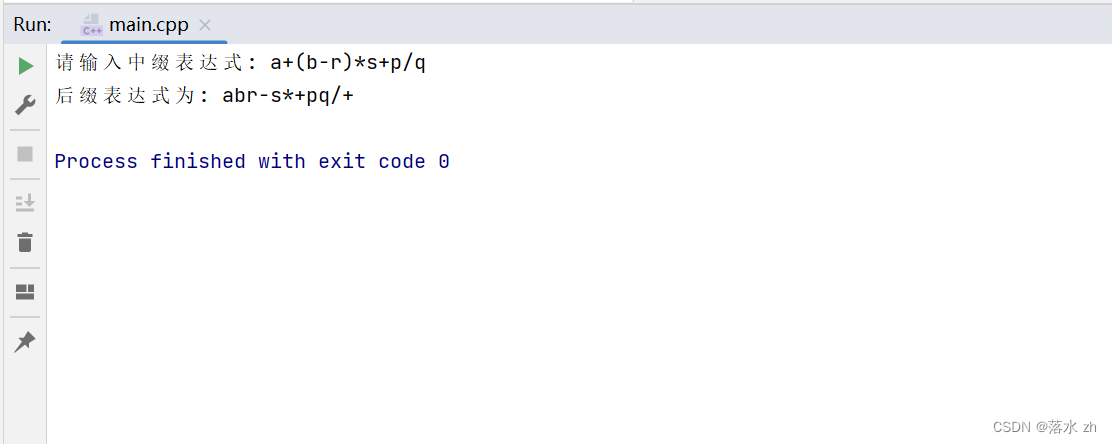
cout << "请输入中缀表达式: ";
cin >> infix;
// 调用infixToPostfix函数将输入的中缀表达式转换为后缀表达式,并存储在postfix变量中
string postfix = infixToPostfix(infix);
// 输出转换后的后缀表达式
cout << "后缀表达式为: "<< postfix<< endl;
// 程序结束,返回0
return 0;
}
后缀转中缀
后缀转中缀思路就是逆着上面的思路,力扣上面有一道类似的题:
https://leetcode.cn/problems/8Zf90G/description/
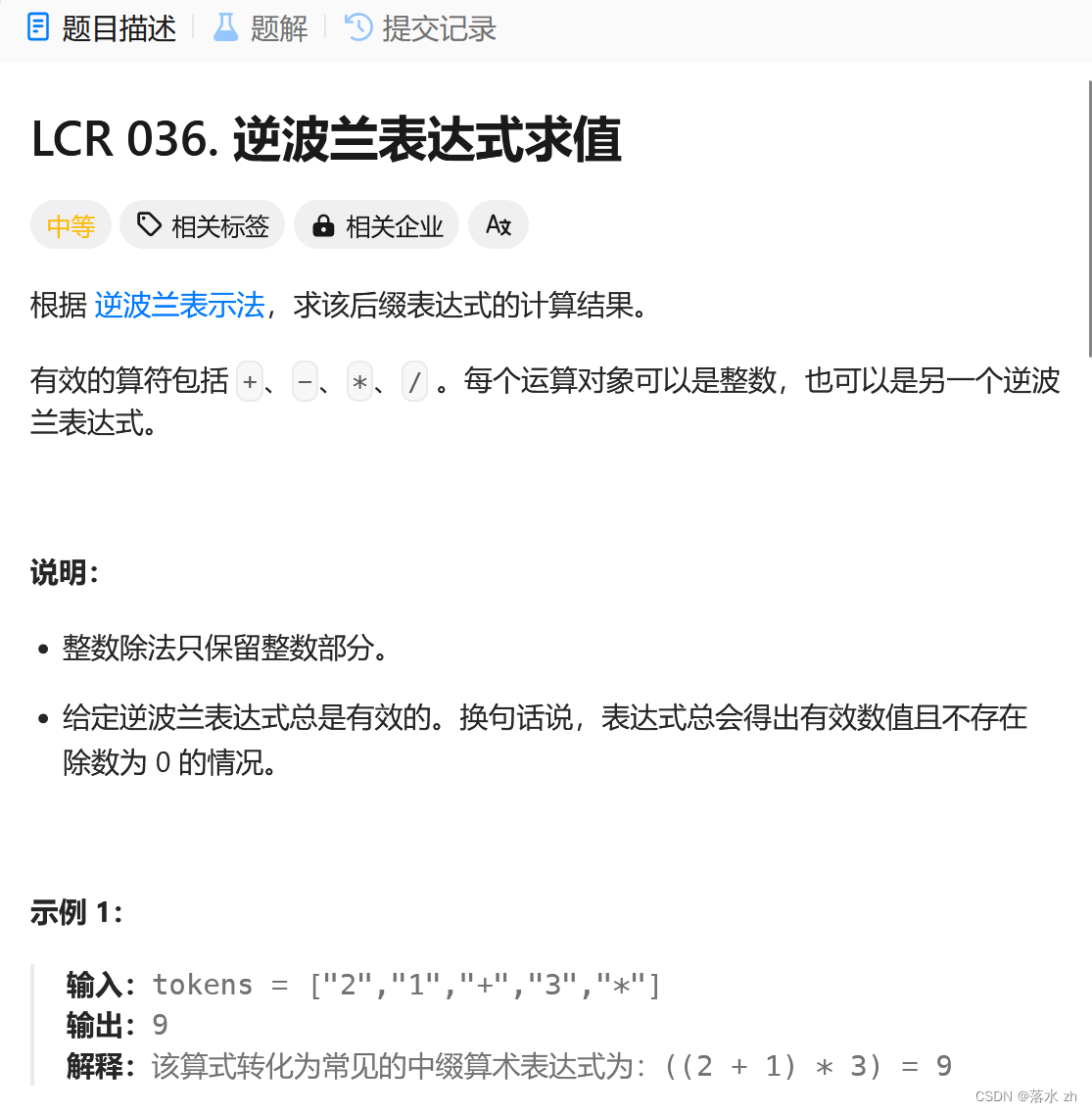
力扣上面有比较全面的解析,这里不再赘述,大家可以去看官方解答:
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> stk;
int n = tokens.size();
for (int i = 0; i < n; i++) {
string& token = tokens[i];
if (isNumber(token)) {
stk.push(atoi(token.c_str()));
} else {
int num2 = stk.top();
stk.pop();
int num1 = stk.top();
stk.pop();
switch (token[0]) {
case '+':
stk.push(num1 + num2);
break;
case '-':
stk.push(num1 - num2);
break;
case '*':
stk.push(num1 * num2);
break;
case '/':
stk.push(num1 / num2);
break;
}
}
}
return stk.top();
}
bool isNumber(string& token) {
return !(token == "+" || token == "-" || token == "*" || token == "/");
}
};

![[iOS]使用CocoaPods发布公开库](https://img-blog.csdnimg.cn/direct/23755e62033e441bbcb8f92c929df518.png)