思考题1


改进cosx?优化算法
关键点在于cos计算过于麻烦,而每次都要求sinx的值
故直接简化为cosx的导数 -sinx
即:
原://double daoshu(double x) {
// return 18 * x - cos(x);
//}
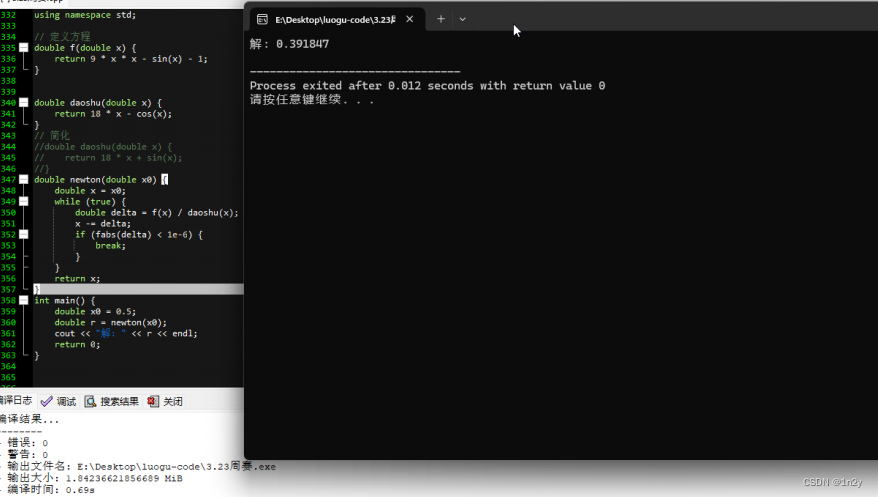
改:double daoshu(double x) {
return 18 * x + sin(x);
}
证明:

思考题2:

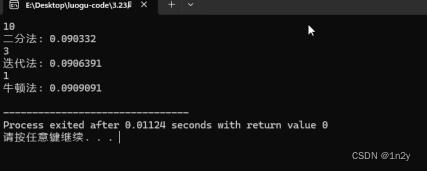
c++代码如下:
// 二分法
double bin(double l, double r) {
double eps = 1e-3;
while (r - l > eps) {
double mid = (l + r) / 2;
double f = exp(mid) + 10 * mid - 2;
if (f > 0) {
r = mid;
} else {
l = mid;
}
}
return (l + r) / 2;
}
// 迭代法
double ite() {
double x = 0;
double eps = 1e-3;
while (1) {
double x1 = (2 - exp(x)) / 10;
if (x - x1 > eps) {
break;
}
x = x1;
}
return x;
}
// 牛顿法
double new() {
double x = 0;
double eps = 1e-3;
while (1) {
double f = exp(x) + 10 * x - 2;
double df = exp(x) + 10;
double x1 = f / df;
if (x1 > eps) {
break;
}
x = x - x1;
}
return x;
}
思考题3:
求谱半径?

思考题4:



代码实现:
double Max(vectorx) {
double max = x[0];
int n = x.size();
for (int i = 0; i < n; i++)
if (x[i] > max) max = x[i];
return max;
}
void Jacobi(vector<vector > A, vector B, int n) {
vector X(n, 0);
vector Y(n, 0);
vector D(n, 0);
int k = 0;
do {
X = Y;
for (int i = 0; i < n; i++) {
double tem = 0;
for (int j = 0; j < n; j++) {
if (i != j) tem += A[i][j] * X[j];
}
Y[i] = (B[i] - tem) / A[i][i];
cout << left << setw(8) << Y[i] << " ";
}
cout << endl;
k++;
if (k > 100) {
return;
}
for (int a = 0; a < n; a++) {
D[a] = X[a] - Y[a];
}
} while (fabs(Max(D)) > 1e-4);
return;
}
int main() {
int n;
cout << "未知数的个数n:";
cin >> n;
cout << endl;
vector<vector>A(n, vector(n, 0));
vectorB(n, 0);
cout << "系数矩阵:" << endl;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> A[i][j];
}
}
cout << endl;
cout << "值矩阵:" << endl;
for (int k = 0; k < n; k++) {
cin >> B[k];
}
cout << endl;
cout << "您输入的方程组为:" << endl;
for (int a = 0; a < n; a++) {
for (int b = 0; b < n; b++) {
cout << A[a][b] << " ";
}
cout << " " << B[a] << endl;
}
cout << endl;
cout << "方程组的解:" << endl;
Jacobi(A, B, n);
return 0;
}结果:
思考题5:
.ACM
大赛预测计算名次
甲第一,乙第三。
丙第一,丁第四。
丁第二,甲第三。
都只说对一半
计算名次
代码:
int main()
{
//甲乙丙丁:ABCD
int a,b,c,d;
for(a=1;a<=4;++a)
{
for(b=1;b<=4;++b)
{
if(a!=b)
for(c=1;c<=1;++c)
{
d=10-a-b-c;
if(((a==1)+(b==3)==1)&&( (c==1)+(d==4 )==1)&&((a==3)+(d==2)==1 ) )
{
cout<<"甲:"<<a<<"乙:"<<b<<"丙:"<<c<<"丁:"<<d<<endl;
break;
}
}
}
}
return 0;
}结果:
思考题6:

思考题7: